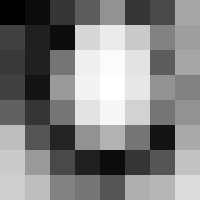히스토그램 등분화
Histogram equalization히스토그램 등화(Histogram Equalization)는 이미지의 히스토그램을 이용한 대비 조정의 이미지 처리 방법이다.null
개요
이 방법은 일반적으로 많은 영상의 전역 대비를 증가시키며, 특히 영상이 좁은 범위의 강도 값으로 표현되는 경우 더욱 그러하다.이 조정을 통해 히스토그램에서 전체 강도 범위를 고르게 활용하여 강도를 더 잘 분배할 수 있다.이것은 국소 대비가 낮은 영역이 더 높은 대비를 얻을 수 있게 한다.히스토그램 평준화는 이미지 대비를 저하시키는 데 사용되는 고도로 채워진 강도 값을 효과적으로 분산시킴으로써 이를 달성한다.null
이 방법은 밝거나 어두운 배경과 전경을 가진 이미지에서 유용하다.특히 이 방법은 X선 영상에서 뼈 구조를 더 잘 볼 수 있게 하고, 지나치게 노출되거나 적게 노출되는 사진에서 더 자세히 볼 수 있게 할 수 있다.이 방법의 주요 장점은 입력 이미지에 적응하는 상당히 간단한 기법이며, 변환 불가능한 연산자라는 것이다.따라서 이론적으로 히스토그램 등화 함수를 알면 원래의 히스토그램을 복구할 수 있다.그 계산은 계산적으로 집약적이지 않다.이 방법의 단점은 무차별적이라는 것이다.사용 가능한 신호는 줄이면서 배경 노이즈의 대비를 증가시킬 수 있다.null
신호의 강도(정량화된 길이의 DNA 조각을 분리하는 등)보다 공간적 상관관계가 더 중요한 과학 영상촬영에서 작은 신호 대 잡음 비율은 보통 시각적 감지를 방해한다.null
히스토그램 평준화는 종종 사진에서 비현실적인 효과를 만들어내지만 열, 위성 또는 X선 영상과 같은 과학적인 이미지에 매우 유용하며 종종 거짓 색상을 적용하는 것과 같은 등급의 이미지에도 유용하다.또한 히스토그램 등분화는 컬러 깊이가 낮은 영상에 적용할 때 바람직하지 않은 효과(예: 가시적인 영상 그라데이션)를 발생시킬 수 있다.예를 들어, 8비트 그레이 스케일 팔레트로 표시된 8비트 이미지에 적용하면 이미지의 색 깊이(회색의 고유한 음영 수)가 더욱 감소한다.연속 데이터나 16비트 그레이스케일 영상처럼 팔레트 크기보다 색 농도가 훨씬 높은 영상에 적용할 경우 히스토그램 이퀄라이제이션이 가장 효과적이다.null
히스토그램 동등화를 이미지 변화로 생각하고 구현하는 방법에는 두 가지가 있다.연산은 P(M(I)로 표현할 수 있으며 여기서 I는 원본 이미지, M은 히스토그램 등화 매핑 작업, P는 팔레트다.새로운 팔레트를 P'=P(M)로 정의하고 이미지 I를 변경하지 않은 상태로 두면 팔레트 변경 또는 매핑 변경으로 히스토그램 동등화가 구현된다.반면에 팔레트 P가 변하지 않고 이미지가 I'=M(I)으로 수정되면 이미지 변경에 의해 구현이 이루어진다.대부분의 경우 팔레트 변경은 원래 데이터를 보존하기 때문에 더 좋다.null
이 방법의 수정은 하위 히스토그램이라 불리는 다중 히스토그램을 사용하여 전체적인 글로벌 대비보다는 국소 대비를 강조한다.그러한 방법의 예로는 적응형 히스토그램 등화, 적응형 히스토그램 등화 또는 CLAHE를 제한하는 대조도, 다중극 히스토그램 등화(MPHE), 다목적 베타 최적화 생물히스토그램 등화(MBOBHE) 등이 있다.이러한 방법들, 특히 MBOBHE의 목적은 HE 알고리즘을 수정하여 밝기 평균 이동 및 상세 손실 아티팩트를 생성하지 않고 대비를 개선하는 것이다.[1]null
히스토그램 평준화에 해당하는 신호 변환은 입력 통계 함수로서 뉴런의 출력 발화 속도를 극대화하기 위해 생물학적 신경망에서도 일어나는 것 같다.이것은 특히 파리망막에서 증명되었다.[2]null
히스토그램 동일화는 히스토그램 재매핑 방법의 보다 일반적인 클래스의 특정한 경우다.이러한 방법은 시각적 품질을 쉽게 분석하거나 개선할 수 있도록 이미지 조정을 모색한다(예: 레티넥스).
백 투영
히스토그램 영상의 백 투영(또는 "프로젝트")은 수정된 히스토그램을 원래 영상에 다시 적용하는 것으로 픽셀 밝기 값에 대한 조회 테이블 역할을 한다.null
모든 입력 단일 채널 영상에서 동일한 위치에서 가져온 각 픽셀 그룹에 대해 함수는 히스토그램 빈 값을 대상 영상에 배치하고, 여기서 빈의 좌표는 이 입력 그룹의 픽셀 값에 의해 결정된다.통계적으로 각 출력 영상 픽셀의 값은 해당 입력 픽셀 그룹이 히스토그램이 사용되는 객체에 속할 확률을 특징으로 한다.[3]null
실행
이산형 그레이스케일 이미지 {x}을(를) 고려하고 n을i 그레이 레벨 i의 발생 횟수로 설정하십시오.영상에서 레벨 i 픽셀이 발생할 확률은
\은(는) 영상의 총 회색 수준 수(일반적으로 256), n은 영상의 총 픽셀 수(픽셀 수)이며, p () 은 실제로 픽셀 값 i에 대한 영상의 히스토그램이며, [0,1]으로 정규화되었다.null
또한 i에 해당하는 누적분포함수를 다음과 같이 정의하자.
- ( i)= j= 0 (x = )
또한 영상의 누적 정규화된 히스토그램이기도 하다.null
= ( x) \ y 형식의 변환을 생성하여 평면 히스토그램이 있는 새 이미지 {y}을(를) 생성하고자 한다.그러한 이미지는 값 범위 전체에 걸쳐 선형화된 누적분포함수(CDF)를 가질 것이다.
- ( i)=( + ) i
일부 상수 \ CDF의 속성은 이러한 변환을 수행할 수 있게 해준다(역분포함수 참조). 이 변환은 다음과 같이 정의된다.
여기서 \은는) [ - 의 범위 내에 있다 {x}의 정규화된 히스토그램을 사용했기 때문에 은(는) 수준을 [0, 범위로 매핑한다는 점에 유의하십시오.값을 원래 범위로 다시 매핑하기 위해서는 다음과 같은 간단한 변환을 결과에 적용할 필요가 있다.
\은(는) 실제 값이고 \은(는) 정수여야 한다.직관적이고 널리 사용되는 방법은[4] 다음과 같은 원형 작동을 적용하는 것이다.
- = ( ( - 1)\
그러나 상세한 분석 결과 공식은 약간 다르다.1/L이 이 매핑 된 값(′{\displaystyle)y^{\prime}}가 되어야 한다 00의 범위, 베≤ 1/L{0<, y\leq 1/L\displaystyle}. 그리고 y′=1{\displaystyle)y^{\prime}=1}<> 베≤ 2/L{1/L<, y\leq 2/L\displaystyle}, y′=2{\displaystyle)y^{\prime}=2}2/. 나는<>y ≤ 3, ...., and finally for . Then the quantization formula from to should be
= ( y)- y.
(참고: =- = 0 \일 때, = 0 \이(가) 해당 값에 해당하는 픽셀이 없음을 의미한다고 해서 발생하는 것은 아니다.)null
컬러 이미지
위에서는 그레이스케일 영상의 히스토그램 등분화에 대해 설명한다.단, 이미지의 RGB 색상 값의 적색, 녹색, 청색 구성 요소에 동일한 방법을 별도로 적용하여 컬러 영상에도 사용할 수 있다.그러나 RGB 영상의 적색, 녹색 및 청색 구성 요소에 동일한 방법을 적용하면 알고리즘을 적용한 결과로 컬러 채널의 상대적 분포가 변경되기 때문에 영상의 색상 균형에 급격한 변화가 발생할 수 있다.단, 영상이 특히 다른 색 공간, Lab 색상 공간, 또는 HSL/HSV 색상 공간으로 먼저 변환되는 경우, 이미지의 색조 및 포화도를 변경하지 않고 휘도 또는 값 채널에 알고리즘을 적용할 수 있다.[5]3D 공간에는 여러 히스토그램 등화 방법이 있다.트라하니아스와 베네사노풀로스는 3D 컬러[6] 공간에 히스토그램 등분화를 적용했지만 밝은 화소의 확률이 어두운 화소보다 높은 '화이트닝'을 초래한다.[7]한 외는 균일한 회색 분포를 초래하는 ISO-후원 평면에 의해 정의된 새로운 cdf를 사용할 것을 제안했다.[8]null
예
통계적 사용과의 일관성을 위해 "CDF"(즉, 누적분포함수)를 "누적 히스토그램"으로 대체해야 하는데, 특히 기사는 누적분포함수의 값을 픽셀의 전체 양으로 나누어 도출한 누적분포함수에 연결하기 때문이다.균등화된 CDF는 k/ x c o o t {\의 등급으로 정의된다
작은 이미지
표시된 8비트 그레이스케일 이미지에는 다음 값이 있다.
| 52 | 55 | 61 | 59 | 79 | 61 | 76 | 61 |
|---|---|---|---|---|---|---|---|
| 62 | 59 | 55 | 104 | 94 | 85 | 59 | 71 |
| 63 | 65 | 66 | 113 | 144 | 104 | 63 | 72 |
| 64 | 70 | 70 | 126 | 154 | 109 | 71 | 69 |
| 67 | 73 | 68 | 106 | 122 | 88 | 68 | 68 |
| 68 | 79 | 60 | 70 | 77 | 66 | 58 | 75 |
| 69 | 85 | 64 | 58 | 55 | 61 | 65 | 83 |
| 70 | 87 | 69 | 68 | 65 | 73 | 78 | 90 |
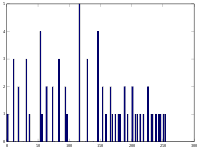
이 영상의 히스토그램은 다음 표에 나와 있다.0을 가진 픽셀 값은 간결성을 위해 제외된다.null
가치 카운트 가치 카운트 가치 카운트 가치 카운트 가치 카운트 52 1 64 2 72 1 85 2 113 1 55 3 65 3 73 2 87 1 122 1 58 2 66 2 75 1 88 1 126 1 59 3 67 1 76 1 90 1 144 1 60 1 68 5 77 1 94 1 154 1 61 4 69 3 78 1 104 2 62 1 70 4 79 2 106 1 63 2 71 2 83 1 109 1
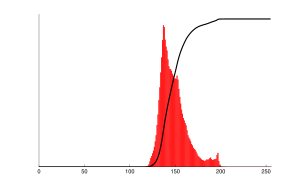
누적분포함수(cdf)는 다음과 같다.다시 말하지만, cdf의 증가에 기여하지 않는 픽셀 값은 간결성을 위해 제외된다.null
( )= (( ) - 1 h( {operatorname { 버전은 아직 나와 있지 않다는 점에 유의하십시오.)v, 픽셀 강도 cdf(v) h(v), Equalized v 52 1 0 55 4 12 58 6 20 59 9 32 60 10 36 61 14 53 62 15 57 63 17 65 64 19 73 65 22 85 66 24 93 67 25 97 68 30 117 69 33 130 70 37 146 71 39 154 72 40 158 73 42 166 75 43 170 76 44 174 77 45 178 78 46 182 79 48 190 83 49 194 85 51 202 87 52 206 88 53 210 90 54 215 94 55 219 104 57 227 106 58 231 109 59 235 113 60 239 122 61 243 126 62 247 144 63 251 154 64 255
이 cdf는 서브이미지의 최소값이 52이고 최대값이 154라는 것을 보여준다.값 154의 cdf는 영상의 픽셀 수와 일치한다.cdf는[ 으)로 정규화해야 한다일반적인 히스토그램 등화 공식은 다음과 같다.
여기서 cdf는min 누적분포함수의 최소 0이 아닌 값(이 경우 1), M × N은 이미지의 픽셀 수(예: M은 너비, N은 높이)를 부여하고 L은 사용된 회색 수준 수(대부분의 경우, 이 값, 256)이다.null
0을 초과하는 원본 데이터의 값을 1에서 L-1까지(포함)로 스케일링하려면 위의 방정식은 대신 다음과 같을 것이다.
여기서 cdf(v) > 0. 1에서 255까지의 스케일링으로 최소값의 0이 아닌 값을 보존한다.null
0에서 255까지의 스케일링 데이터의 예에 대한 등분화 공식은 다음과 같다.
예를 들어, 78의 cdf는 46이다. (78의 값은 7번째 열의 맨 아래 줄에 사용된다.)표준화된 값이
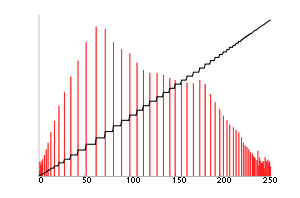
이 작업이 완료되면 평준화된 cdf에서 평준화된 영상의 값을 직접 가져와 평준화된 값을 산출한다.
| 0 | 12 | 53 | 32 | 190 | 53 | 174 | 53 |
|---|---|---|---|---|---|---|---|
| 57 | 32 | 12 | 227 | 219 | 202 | 32 | 154 |
| 65 | 85 | 93 | 239 | 251 | 227 | 65 | 158 |
| 73 | 146 | 146 | 247 | 255 | 235 | 154 | 130 |
| 97 | 166 | 117 | 231 | 243 | 210 | 117 | 117 |
| 117 | 190 | 36 | 146 | 178 | 93 | 20 | 170 |
| 130 | 202 | 73 | 20 | 12 | 53 | 85 | 194 |
| 146 | 206 | 130 | 117 | 85 | 166 | 182 | 215 |
최소값(52)은 현재 0이고 최대값(154)은 현재 255라는 점에 유의하십시오.null
풀사이즈 이미지
참고 항목
메모들
- ^ Hum, Yan Chai; Lai, Khin Wee; Mohamad Salim, Maheza Irna (October 11, 2014). "Multiobjectives bihistogram equalization for image contrast enhancement". Complexity. 20 (2): 22–36. Bibcode:2014Cmplx..20b..22H. doi:10.1002/cplx.21499.
- ^ Laughlin, S.B (1981). "A simple coding procedure enhances a neuron's information capacity". Z. Naturforsch. 9–10(36):910–2.
- ^ Intel Corporation (2001). "Open Source Computer Vision Library Reference Manual" (PDF). Retrieved January 11, 2015.
{{cite journal}}:Cite 저널은 필요로 한다.journal=(도움말) - ^ Gonzalez, Rafael C. (2018). Digital image processing. Richard E. Woods (4th ed.). New York, NY: Pearson. pp. 138–140. ISBN 1-292-22304-9. OCLC 991765590.
- ^ S. Naik과 C.머시, "게뮤트 문제 없이 색상 이미지 개선"이미지 처리, vol. 12, no. 12, 페이지 1591–1598, 2003년 12월
- ^ P. E. Trahanias와 A.N. Venetsanopulos, Proc. 15번째 IAPR Int의 "3-D 히스토그램 동등화를 통한 컬러 이미지 향상"1992년 8월-9월 1, 페이지 545–548, 참조 패턴 인식.
- ^ N. Bassiou와 C.Kotropoulos, "Color image histogram as equalization by 절대 할인 back-off," Computer vision and Image Defense, vol. 107, 1-2, pp.108-122, 2007년 7월-8월.
- ^ Han, Ji-Hee; Yang, Sejung; Lee, Byung-Uk (2011). "A Novel 3-D Color Histogram Equalization Method with Uniform 1-D Gray Scale Histogram". IEEE Transactions on Image Processing. 20 (2): 506–512. doi:10.1109/TIP.2010.2068555. PMID 20801744. S2CID 17972519.
참조
- Acharya and Ray, 이미지 처리: 원리 및 응용, Wiley-Interscience 2005 ISBN 0-471-71998-6
- 러스, 이미지 처리 핸드북: 제4판, CRC 2002 ISBN 0-8493-2532-3
- 5세대에서 "히스토그램 평준화" (iii)


 (는) 영상의 총 회색 수준 수(일반적으로 256), n은 영상의 총 픽셀 수(픽셀 수)이며, p
(는) 영상의 총 회색 수준 수(일반적으로 256), n은 영상의 총 픽셀 수(픽셀 수)이며, p






![{\displaystyle [0,L-1])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/65750fadf4ccfc943115238508d7fdabfa887322)









 때,
때,

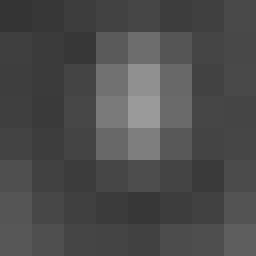

![[0,255]](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b92f49fdc420e36b9d62c711c3c6ebe7d9fcebc)