수평선 시험

수학에서 수평선 시험은 함수가 주입성(즉, 일대일)인지 여부를 판단하는 데 사용되는 시험이다.^[1]

미적분학에서

수평선은 왼쪽에서 오른쪽으로 가는 직선이다.함수 $f{\displaystyle }$: ${\displaystyle R\mathbb{}}$→ R ${\$\mathb {R$}$\$$to \$mathb {$R}}}(즉, 실제 번호에서 실제 번호까지)를 지정하면 함수의 그래프를 교차하는 수평선을 보고 주입 여부를 결정할 수 있다.수평선 $y{\displaystyle }$= ${\displaystyle c}$ ${\displaystyle y=c}$이(가) 둘 이상의 점에서 그래프를 교차하는$$ 경우 함수는 주입되지 않는다.이를 확인하려면 교차점들이 $y-값$은 같지만(선 y${\displaystyle }$= ${\displaystyle c}$ ${\displaystyle y=c}$에 있기 때문에$)$ x 값은 다르며, 정의상 함수는 주입될 수 없다는 것을 의미한다.^[1]

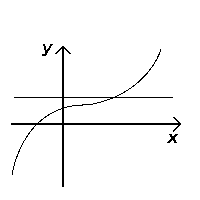테스트 통과(내부적)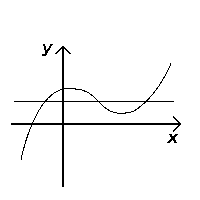

테스트 실패(주입이 아님)

수평선 시험의 변형은 함수가 과부하인지 과부하인지를 결정하는 데 사용될 수 있다.

• 함수 f는 해당 그래프가 수평선과 한 번 이상 교차하는 경우에만 굴절적이다(즉, 위에).
• f는 어떤 수평선이 그래프를 정확히 한 번 교차하는 경우에만 비굴하다.

세트 이론에서

Consider a function ${\displaystyle f\colon X\to Y}$ with its corresponding graph as a subset of the Cartesian product ${\displaystyle X\times Y}$. Consider the horizontal lines in ${\displaystyle X\times Y}$ :${\displaystyle \{(x,y_{$$0}\in$ X$\time Y:y_{0}{\text{은 상수임}\}=X\time \{y_{0$f 함수는 각 수평선이 그래프를 최대 한 번에 교차하는 경우에만 주입된다.이 경우 그래프는 수평선 시험을 통과한다고 한다.어떤 수평선이 그래프와 두 번 이상 교차하면 함수는 수평선 시험에 실패하고 주입되지 않는다.^[2]

참고 항목

• 수직선 시험
• 역함수
• 단조함수

참조