순간 회전 중심

순간 회전 중심(순간 속도 중심,^[1] 순간 중심 또는 순간 중심)은 특정 순간에 속도가 0인 평면 운동을 하는 물체에 고정된 지점입니다.이 때, 체내의 다른 점의 속도 벡터는, 이 점의 주위에 순수 회전에 의해서 발생하는 것과 같은 원형의 필드를 생성한다.

물체의 평면 이동은 종종 2차원 평면상에서 움직이는 평면 도형을 사용하여 묘사된다.순간 중심은 이동 평면에서 다른 모든 점이 특정 순간에 회전하는 지점입니다.

평면의 연속 이동에는 시간 파라미터의 모든 값에 대한 순간 중심이 있습니다.이것은 움직이는 중심이라고 불리는 곡선을 생성합니다.이러한 순간 중심에 해당하는 고정 평면의 점이 고정 중심을 형성합니다.

이 개념을 3차원 공간으로 일반화하는 것은 나사 주위의 비틀림입니다.나사에는 3D 공간의 선인 축이 있으며(원점을 반드시 통과하는 것은 아님), 나사에는 유한한 피치(나사 축을 중심으로 회전하는 것에 대응하는 축을 따라 고정된 변환)가 있습니다.

평면 변위 극

순간 중심은 평면 변위 극의 제한 사례로 간주할 수 있다.

위치 1에서 위치 2로의 물체의 평면 변위는 평면 회전과 평면 변환의 조합으로 정의됩니다.모든 평면 변위에 대해 이동체에는 변위 전후에 동일한 위치에 있는 점이 있습니다.이 점은 평면 변위의 극이며, 변위는 이 극을 중심으로 한 회전으로 볼 수 있습니다.

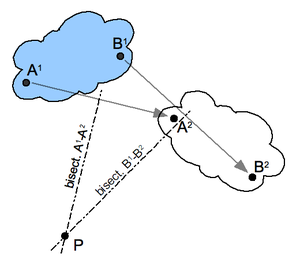
평면 변위 극 구조:먼저 이동체의 두 점 A와 B를 선택하고 두 위치에서 해당하는 점을 찾습니다. 그림을 참조하십시오.두 세그먼트 AA와¹² BB에¹² 수직 이등분선을 구성합니다.이 두 이등분선의 교차점 P는 평면 변위의 극이다.A와² A가 P를 둘러싼 원 위에 놓여¹ 있는 것에 주의해 주세요.이는 신체의 모든 점에 해당하는 위치에 적용됩니다.

평면 운동에서 물체의 두 위치가 순간적으로 떨어져 있으면 변위의 극이 순간 중심이 된다.이 때, 점 A와 점 B의 순간 위치 사이에 구축된 세그먼트가 속도 벡터_A V와_B V가 된다.이러한 속도 벡터에 수직인 선은 순간 중심에서 교차합니다.

${\displaystyle {데카르트}_{}}{\displaystyle 좌표}$의 대수적${\displaystyle {}_{}{}_{}}$(${\displaystyle {}_{}{P}_{}}$x , P y ) { displaystyle $\left(P_{x},P_{$y}\$right)$은 다음과 같이 배열할 수 있습니다.${\displaystyle {A\mathrm{}}^{}}$ 1$({$$$$^{$1})과 A 2$({$displaystyle A$^{2$}) $사이$의 중간점에는 데카르트 좌표가 있습니다.

$({displaystyle A_{x}^{2}=sqfrac {1}{2})\left(A_{x}^{2}\오른쪽),\quad A_{y}^{m}=sqfrac {1}{2}\left(A_{y}^{1}+)A_{y}^{2}\오른쪽}$

$($ ${\displaystyle {스타일\mathrm{}}^{}}$ B$^{1})$과 B2$($ B$^{2})$ $사이$의 중간점에는 직교 좌표가 있습니다.

$({displaystyle B_{x}^{2}=subfrac {1}{2}\left(B_{x}^{2}\오른쪽),\quad B_{y}^{m}=subfrac {1}{2}\left(B_{y}^{2}^{2}\오른쪽).}$

수평에 대해 시계 반대 방향으로 측정된 $($ 스타일 A$^{1})$에서 $($ A$^{2})$ 및$$ $($ B$^{1})$에서 $($ B$^{2})$까지의 2개의 각도는 다음과 같이 결정됩니다.

$({displaystyle \tan \tan _{A}=frac {A_{y}^{1}-A_{x}^{1}-A_{x}^{1},\quad \tan \tan _{B}=frac {B_{y}-B_{y}^{1}){{1}}{{{}}}}}{A_frcfrac {A_frac {A_{{f}}}}{{{{{f}}}}}}{fr}}}}}}{f}}}}}$

접선의 정확한 가지를 취합니다.회전의 중심$({\displaystyle P_{}}$x , ${\displaystyle {}_{}{y}_{}}$)(\$displaystyle$ \left$(P_{x$, $P_{y}\right$$$$)$에 2개의 중간점까지의 거리 $(\$ $및{\displaystyle {}_{}}$ d$$(\$displaystyle d_{$B$$})를 설정합니다.시계 방향으로 회전한다고 가정합니다(그렇지 않으면${\displaystyle }wise{\displaystyle }$ / $(\displaystyle \pi / 2$)의 기호를 바꿉니다).$$

$디스플레이 스타일P_{x}&=A_{x}^{m}+d_{A}\cos \left(\tau _{A}-{\frac {pi }{2}}\오른쪽)\\&=B_{x}^{m}+d_{B}\cos \left(\cos _{B}-{\frac {pi }{2}}\right);\\P_{y}&=A_{y}^{m}+d_{A}\sin \left(\tau _{A}-{\frac {pi }{2}}\right)\\&=B_{y}^{m}+d_{B}\sin \left(\sin _{B}-{\frac {pi }{2}}\오른쪽).\end { aligned}}$

이를 4개의 미지수를 갖는 4×4 비균질 선형 방정식 시스템(중앙의 두 $거리{\displaystyle }$ d$\displaystyle$ d$\$ 및$$ 두 $좌표$ P\$displaystyle$$P\)$으로 다시 씁니다.

${\displaystyle {begin{pmatrix}1&-\sin \tau _{A}\\1&\cos \tau _{A}&0\cos \tau _{B}\end{pmatrix}{pmatrix}{pm}{pmatrix}{pmatrix}\\cos}P_{y}\\d_{A}\\d_{B}\end{pmatrix}=begin{pmatrix}A_{x}^{m}\B_{x}^{m}\\A_{y}^{m}\\B_{y}^{m}\end{pmatrix}}.}$

회전 중심 좌표는 솔루션 벡터의 처음 두 가지 성분입니다.

$(\displaystyle\begin{pmatrix}P_{x}\\)P_{y}\\d_{A}\\d_{B}\end{pmatrix}=flac {1}{\sin \left(\sin _{A}-\tau _{B}\오른쪽)}{\begin{pmatrix}\left(B_{y}^{m}-A_{y}^{m}\오른쪽)\sin \tau _{B}+B_{x}^{m}\sin \tau _{A}\cos \tau _{m}cos\tauA_{y}^{m}\sin \tau _{A}\cos \tau _{B}-{y}^{m}\cos \tau _{A}\sin \tau _{B}\left (B_{x}^{m}\right)\cos \tau _{B}\cos \tau _{B}}$

순수 번역

두 위치 사이의 변위가 순수 변환일 경우 세그먼트¹¹ AB와²² AB의 수직 이등분선이 평행선을 형성합니다.이 선들은 무한대의 선상에서 교차하는 것으로 간주되며, 따라서 이 평면 변위의 극은 수직 이등분선 방향으로 "무한대에 놓여 있다"고 한다.

한계에서 순수 변환은 평행한 점 속도 벡터를 가진 평면 운동이 된다.이 경우 순간 중심은 속도 벡터에 수직인 방향으로 무한대에 있다고 한다.

미끄러지지 않고 휠이 순간적으로 회전하는 중심

선형 도로에서 미끄러지지 않는 원형 바퀴의 평면 움직임을 고려합니다. 스케치 3을 참조하십시오.휠은 축 M을 중심으로 회전하며, 이는 도로와 평행한 방향으로 변환됩니다.바퀴와 도로의 접촉점 P는 미끄러지지 않으며, 이는 도로와 관련하여 P의 속도가 0임을 의미합니다.따라서 바퀴의 P점은 도로와 접촉하는 순간 순간 중심이 된다.

순간 중심이 되는 움직이는 바퀴의 점 세트는 움직이는 중심을 정의하는 원 그 자체입니다.이러한 순간 중심에 해당하는 고정 평면의 점이 도로의 선이며, 이 선이 고정 중심을 정의합니다.

휠 내 점 A의 속도 벡터는 세그먼트 AP에 수직이며 이 세그먼트의 길이에 비례합니다.특히 P를 중심으로 회전하는 바퀴의 각속도에 의해 바퀴 내 점의 속도가 결정된다.여러 지점의 속도 벡터는 스케치 3에 나와 있습니다.

휠의 한 지점이 순간 중심 P에서 멀어질수록 속도는 비례적으로 커집니다.따라서, 휠의 상단의 점은 휠의 중심 M과 같은 방향으로 이동하지만, P에서 두 배 떨어져 있기 때문에 2배 더 빠릅니다.P 지점으로부터 휠 'r'의 반지름과 동일한 거리인 모든 지점은 M 지점과 같은 속도로 이동하지만 다른 방향으로 이동한다.이는 M과 같은 속도를 가지지만 P 주위의 원에 접하는 방향으로 이동하는 휠의 한 점에 대해 표시됩니다.

접촉하는 두 개의 평면체에 대한 상대 회전 중심

두 개의 평면 강체가 접촉하고 각 물체에 고유한 회전 중심이 있는 경우, 물체 간의 상대적 회전 중심은 두 중심을 연결하는 선상의 어딘가에 있어야 합니다.그 결과, 순압연이란 회전중심이 접촉점에 있을 때만 존재할 수 있기 때문에(위에서 본 바와 같이) 2개의 회전중심을 연결하는 선을 통과해야 순압연임을 실현할 수 있다.이는 인볼루트 기어 설계에서 피치 포인트로 알려져 있으며, 기어 사이에 상대적인 슬라이딩이 없습니다.실제로 2개의 회전부 사이의 기어비는 상대중심과의 2개의 거리 비율에 의해 구해진다.스케치 4의 예에서 기어비는 ${\displaystyle =}$ ${\displaystyle A\frac{}{}}$ ${\displaystyle \frac{}{}}$ B$$(\$displaystyle\displaystyle$\display =$frac {AD}{BD}})$입니다.

회전 및 메커니즘의 즉각적인 중심

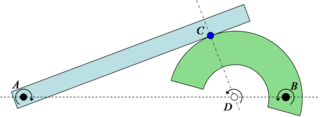
위의 스케치 1은 다수의 순간 회전 중심이 표시된 4개의 막대 링크를 보여줍니다.문자 BAC로 표시된 강체는 베이스 또는 프레임에 대한 링크 P-A₁ 및 P-B로₂ 연결됩니다.

이 메커니즘의 3가지 이동 부분(베이스가 이동하지 않음)은 링크 P-A₁, 링크 P-B₂ 및 바디 BAC입니다.이 세 부분 각각에 대해 순간 회전 중심을 결정할 수 있다.

첫 번째 링크 P-A를₁ 고려: 포인트A를 포함한 이 링크의 모든 포인트는 포인트₁ P를 중심으로 회전합니다.P는 주어진 평면에서 움직이지 않는 유일한 점이기 때문에₁ 이 링크의 순간 회전 중심이라고 할 수 있습니다.P로부터의 거리₁ P-A에서₁ A점은 벡터_A V로 나타내듯이 링크 P-A에₁ 수직인 방향으로 원운동으로 이동한다.

링크 P-B에도₂ 마찬가지입니다.포인트₂ P는 이 링크의 순간 회전 중심이며 포인트 B는 벡터_B V에 표시된 방향으로 이동합니다.

링크의 제3요소인 본체 BAC, 2점 A, B의 순간 회전 중심을 결정하기 위해서는 링크 P-A₁, P-B에₂ 관한 정보로부터 그 이동 특성을 알 수 있기 때문에 이용한다.

A 지점의 속도 방향은 벡터_A V로 표시됩니다.V가 원의 원주에 접선 방향으로 위치하기 때문에 즉각적인_A 회전 중심은 이 벡터에 수직이어야 합니다.요건을 충족하는 유일한 회선은 링크 P-A를₁ 가진 회선입니다.이 선상의 어딘가에 BAC의 순간 회전 중심인 P점이 있습니다.

점 A에 적용되는 것은 점 B에도 적용됩니다.따라서 이 순간적인 회전 중심 P는₂ 링크 P-B와 직교하는 선인_B 벡터 V에 수직인 선상에 위치합니다.따라서 본체 BAC의 순간 회전 중심 P는₁ P-A와₂ P-B를 통과하는 선이 교차하는 지점이다.

이 순간 회전 중심 P는 임의의 점, 예를 들어 점 C에 대한 신체 BAC 상의 모든 점의 중심이기 때문에 이동 속도와 방향을 결정할 수 있습니다. 즉, P를 C에 연결합니다.점 C의 이동 방향은 이 연결부에 수직입니다.속도는 P 지점까지의 거리에 비례합니다.

2개의 링크 P-A₁ 및 P-B가₂ 자신의 순간 회전 중심을 중심으로 회전하면서 이 접근방식을 계속하면 순간 회전 중심 P에 대한 중심을 결정할 수 있다.이를 통해 C 또는 신체 BAC 상의 다른 점에 대한 이동 경로를 결정할 수 있다.

적용 예

생체역학 연구에서는 상단과 ^[2]하단의 관절 기능을 위해 순간 회전 중심이 관찰된다.예를 들어 무릎,^{[3][4][5] [6]}발목 또는 어깨 ^[7][8]관절을 분석할 때 사용합니다.이러한 지식은 팔꿈치나 손가락 ^[10]관절과 같은 인공 관절과 보철물을 개발하는 데 도움이 됩니다.

말의 관절에 대한 연구: "순간 회전 중심에서 결정된 속도 벡터는 관절 표면이 ^[11]서로 미끄러지는 것을 나타냅니다."

물 ^[12]속을 이동하는 선박을 회전시키는 연구.

자동차의 제동 ^[13]특성은 브레이크 페달 메커니즘의 설계를 변경함으로써 개선될 수 있다.

자전거나 ^[14][15]자동차의 서스펜션을 디자인하는 것.

전방의 더블위시본 서스펜션 등 4바 링크의 커플러 링크의 경우 속도에 대한 수직은 접지링크를 따라 커플러 링크에 결합한다.이 구조는 서스펜션의 운동학적 롤 중심을 설정하는 데 사용됩니다.

「 」를 참조해 주세요.

• 센트로이드
• 롤 센터
• 나사축
• 강체
• 고정 축을 중심으로 회전
• 각속도
• 버메스터 이론

레퍼런스