일차방정식

이 문서에는 일반 참조 목록이 포함되어 있지만 해당 인라인 인용이 충분하지 않습니다. 좀 더 정확한 인용문을 소개하여 이 글을 개선할 수 있도록 도와주시기 바랍니다. (2015년 10월) (본 템플릿 메시지 삭제 방법 및 시기 알아보기)

수학에서 선형 방정식(linear equation)은 동일한 변수를 포함하는 하나 이상의 선형 방정식의 집합입니다.^[1]예를들면,

${\displaystyle {\begin{case}3x+2y-z=1\2x-2y+4z=-2\-x+{\frac {1}{2}}y-z=0\end{case}}$

는 3개의 변수 x, y, z에 있는 3개의 방정식 체계입니다.선형 시스템의 해는 모든 방정식이 동시에 만족되도록 변수에 값을 할당하는 것입니다.위의 시스템에 대한 해결책은 순서대로 세배로 제공됩니다.

${\displaystyle(x,y,z)=(1,-2,-2),}$

세 개의 방정식을 모두 유효하게 만들기 때문입니다."시스템"이라는 단어는 방정식을 개별적으로 고려하는 것이 아니라 종합적으로 고려해야 한다는 것을 나타냅니다.

선형 체계는 대부분의 현대 수학에서 사용되는 과목인 선형 대수의 기본이자 기본적인 부분입니다.해를 찾기 위한 계산 알고리즘은 수치 선형 대수학의 중요한 부분이며 공학, 물리학, 화학, 컴퓨터 과학 및 경제학에서 중요한 역할을 합니다.비선형 방정식의 시스템은 종종 선형 시스템(선형화 참조)에 의해 근사화될 수 있는데, 이는 비교적 복잡한 시스템의 수학적 모델이나 컴퓨터 시뮬레이션을 만들 때 유용한 기술입니다.

이 기사에서는 방정식의 계수가 실수 또는 복소수이고 해가 같은 수의 집합에서 검색되지만 이론과 알고리즘은 어떤 분야에서든 계수와 해를 적용합니다.정수의 환과 같은 적분 영역에 있는 해나 다른 대수적 구조에서 다른 이론이 개발된 경우, 환 위의 선형 방정식을 참조하십시오.정수 선형 프로그래밍은 "최상의" 정수 솔루션을 찾기 위한 방법의 모음입니다(많은 경우).그뢰브너 기저 이론은 계수와 미지수가 다항식일 때 알고리즘을 제공합니다.열대 기하학은 더 이국적인 구조의 선형대수학의 또 다른 예입니다.

기본적인 예

사소한 예시

하나의 방정식 체계를 알 수

${\displaystyle 2x=4}$

해결책이 있습니다.

${\displaystyle x=2.}$

그러나 선형 시스템은 일반적으로 적어도 두 개의 방정식을 갖는 것으로 간주됩니다.

단순한 사소한 예

가장 단순한 종류의 자명하지 않은 선형 시스템은 두 개의 방정식과 두 개의 변수를 포함합니다.

${\displaystyle {\begin{alignat}{5}2x&;+\n&3y&;=\n&6&\4x&;+\n9y&;=\n&15.\end{alignedat}}$

이러한 시스템을 해결하기 위한 한 가지 방법은 다음과 같습니다.먼저 $x{\displaystyle }$ ${\displaystyle x}$에 대한 상위 방정식을 $y{\displaystyle }$ ${\displaystyle y}$로 해결합니다$.$

${\displaystyle x=3-{\frac {3}{2}}y.}$

이제 이 식을 x에 대입하여 아래의 식에 대입합니다.

${\displaystyle 4\left(3-{\frac {3}{2}}y\right)+9y=15.}$

따라서 변수 $y$ ${\displaystyle y}$만을 포함하는 단일 방정식이 됩니다$.$ 이를 $풀면$ y = ${\$$displaystyle$ y=1$}$이(가) 주어지고, 이를 x {\displaystyle x}에 대한 방정식에 다시 대입하면 x = 32 {\displaystyle x = {\frac {3}{2}}이(가) 나옵니다. 이 방법은 추가 변수가 있는 시스템에 일반화됩니다(아래 "변수 제거" 참조).또는 기초 대수에 관한 기사.)

일반형

n개의 미지수와 계수를 갖는 m개의 선형 방정식의 일반적인 체계는 다음과 같이 쓸 수 있습니다.

${\displaystyle {\begin{case}a_{11}x_{1}+a_{12}x_{2}+\dots +a_{1n}x_{n}+b_{1}=0\a_{21}x_{1}+a_{22}x_{2}+\dots +a_{2n}x_{n}+b_{2}=0\\\vdots \\a_{m1}x_{1}+a_{m2}x_{2}+\dots +a_{mn}x_{n}+b_{m}=0,\end{case}}$

where ${\displaystyle x_{1},x_{2},\dots ,x_{n}}$ are the unknowns, ${\displaystyle a_{11},a_{12},\dots ,a_{mn}}$ are the coefficients of the system, and ${\displaystyle b_{1},b_{2},\dots ,b_{m}}$ are the constant terms.^[2]

종종 계수와 미지수는 실수 또는 복소수이지만, 추상 대수 구조의 다항식과 원소와 마찬가지로 정수와 유리수도 보입니다.

벡터 방정식

한 가지 매우 유용한 관점은 각 미지가 선형 조합의 열 벡터에 대한 가중치라는 것입니다.

${\displaystyle x_{1}{\begin{bmatrix}a_{11}\a_{21}\\vdots \\a_{m1}\end{bmatrix}}+x_{2}{\begin{bmatrix}a_{12}\\a_{22}\\vdots \\a_{m2}\end{bmatrix}}+\dots +x_{n}{\begin{bmatrix}a_{1n}\a_{2n}\\vdots \\a_{mn}\end{bmatrix}+{\begin{bmatrix}b_{1}\b_{2}\\\vdots \b_{m}\end{bmatrix}=0}$

이를 통해 벡터 공간(또는 더 일반적으로 모듈)의 모든 언어와 이론을 구현할 수 있습니다.예를 들어, 왼쪽에 있는 벡터들의 가능한 모든 선형 조합들의 집합을 그들의 스팬이라고 하고, 방정식들은 오른쪽 벡터가 그 스팬 내에 있을 때 해를 갖습니다.만약 그 범위 안에 있는 모든 벡터가 주어진 왼쪽 벡터의 선형 조합으로 정확히 하나의 표현을 갖는다면, 모든 해는 유일합니다.어떤 경우에도 스팬에는 식 하나를 정확하게 보장하는 선형 독립 벡터의 기저가 있고, 그 기저(그 차원)에 있는 벡터의 수는 m 또는 n보다 클 수 없지만 더 작을 수 있습니다.이것은 중요한 이유가 만약 우리가 m개의 독립적인 벡터를 가지면 우변에 관계없이 해가 보장되고 그렇지 않으면 보장되지 않기 때문입니다.

행렬 방정식

벡터 방정식은 다음과 같은 형태의 행렬 방정식과 같습니다.

여기서 A는 m×n 행렬이고, x는 n개의 원소를 갖는 열 벡터이고, b는 m개의 원소를 갖는 열 벡터입니다.^[3]

스팬에 대한 기저에 있는 벡터의 수는 이제 행렬의 순위로 표현됩니다.

해집합

선형 시스템의 해는 각 방정식이₁ 만족되도록₂ 변수 x, x, ..., x에_n 값을 할당하는 것입니다.가능한 모든 솔루션 집합을 솔루션 집합이라고 합니다.^[4]

선형 시스템은 다음과 같은 세 가지 방법 중 하나로 동작할 수 있습니다.

1. 이 시스템은 무한히 많은 해결책을 가지고 있습니다.
2. 이 시스템은 하나의 독특한 솔루션을 가지고 있습니다.
3. 시스템에 해결책이 없습니다.

기하학적 해석

두 변수(x 및 y)를 포함하는 시스템의 경우 각 선형 방정식은 xy 평면의 선을 결정합니다.선형 시스템의 해는 모든 방정식을 만족해야 하기 때문에 해 집합은 이 선들의 교차점이므로 선, 단점 또는 빈 집합입니다.

세 개의 변수에 대해 각 선형 방정식은 3차원 공간의 평면을 결정하며 해 집합은 이들 평면의 교집합입니다.따라서 해 집합은 평면, 선, 단일 점 또는 빈 집합일 수 있습니다.예를 들어, 세 개의 평행 평면에 공통점이 없으므로 방정식의 해 집합은 비어 있습니다. 한 점에서 교차하는 세 개의 평면 방정식의 해 집합은 단일 점입니다. 세 개의 평면이 두 개의 점을 통과하는 경우,그들의 방정식은 적어도 두 가지의 공통적인 해를 가지고 있습니다; 사실 해 집합은 무한하고 이 점들을 통과하는 모든 선에서 구성됩니다.^[5]

n개 변수의 경우 각 선형 방정식은 n차원 공간의 초평면을 결정합니다.해 집합은 이러한 초평면들의 교차점이며, n보다 낮은 차원을 가질 수 있는 평평합니다.

일반행동

일반적으로 선형 시스템의 거동은 방정식의 수와 미지수의 수 사이의 관계에 의해 결정됩니다.여기서 "일반적으로"는 방정식 계수의 특정 값에 대해 다른 동작이 발생할 수 있음을 의미합니다.

• 일반적으로 미지수보다 방정식 수가 적은 시스템은 해가 무한히 많지만 해가 없을 수도 있습니다.이러한 시스템은 과소 결정된 시스템으로 알려져 있습니다.
• 일반적으로 방정식의 수가 같고 알 수 없는 시스템은 하나의 고유한 해를 갖습니다.
• 일반적으로 방정식이 미지수보다 많은 시스템에는 해가 없습니다.이러한 시스템은 과도하게 결정된 시스템이라고도 합니다.

첫 번째 경우 해 집합의 차원은 일반적으로 n - m과 같으며 여기서 n은 변수의 수이고 m은 방정식의 수입니다.

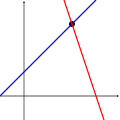
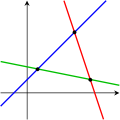
다음 그림은 두 변수의 경우 이 삼분법을 보여줍니다.

1식	투 방정식	삼등식

첫 번째 시스템은 무한히 많은 해결책, 즉 파란색 선의 모든 점들을 가지고 있습니다.두 번째 시스템은 두 선의 교차점이라는 하나의 독특한 해결책을 가지고 있습니다.세 번째 시스템은 세 개의 선이 공통점이 없기 때문에 해결책이 없습니다.

위의 사진들은 가장 일반적인 경우(일반적인 경우)만을 보여준다는 것을 명심해야 합니다.두 개의 방정식과 두 개의 미지수로 이루어진 계는 해가 없거나(두 개의 선이 평행한 경우), 세 개의 방정식과 두 개의 미지수로 이루어진 계는 해가 될 수 있습니다(세 개의 선이 한 점에서 교차하는 경우).

선형 방정식 체계는 방정식이 선형 종속적이거나, 일관성이 없고 미지수보다 더 많은 방정식이 없는 경우 일반적인 경우와 다르게 작용합니다.

특성.

인디펜던스

선형 시스템의 방정식은 어떤 방정식도 다른 방정식들로부터 대수적으로 유도될 수 없다면 독립적입니다.방정식이 독립적인 경우 각 방정식에는 변수에 대한 새로운 정보가 포함되며, 방정식을 제거하면 해 집합의 크기가 증가합니다.선형 방정식의 경우 논리적 독립성은 선형 독립성과 같습니다.

예를 들면, 방정식들은

${\displaystyle 3x+2y=6\;\;\;\;{\text{and}}\;\;\;6x+4y=12}$

독립적이지 않습니다. 이들은 2배로 확장할 때 동일한 방정식이며 동일한 그래프를 생성합니다.이것은 선형 방정식 체계에서의 동등성의 예입니다.

좀 더 복잡한 예를 들자면, 방정식들은

${\displaystyle {\begin{alignat}{5}x&;-\&2y&;=\&&&&&&1&3x&+\&&=\&8&+&=\&7&end{alignat}}$

세 번째 방정식은 다른 두 방정식의 합이기 때문에 독립적이지 않습니다.실제로 이들 방정식 중 어느 하나라도 다른 두 개로부터 유도될 수 있으며, 해 집합에 영향을 주지 않고 어느 하나의 방정식이라도 제거할 수 있습니다.이들 방정식의 그래프는 한 점에서 교차하는 세 개의 선입니다.

일관성.

선형 시스템은 해가 없으면 일관성이 없고, 그렇지 않으면 일관성이 있다고 합니다.^[6]시스템이 일정하지 않을 때 방정식에서 모순을 도출할 수 있으며, 이 모순은 항상 문장 0 = 1로 다시 작성될 수 있습니다.

예를 들면, 방정식들은

${\displaystyle 3x+2y=6\;\;\;\;{\text{and}}\;\;\;3x+2y=12}$

일정하지 않은실제로 두 번째 방정식에서 첫 번째 방정식을 빼고 결과의 양변에 1/6을 곱하면 0 = 1이 됩니다.xy 평면에 있는 이러한 방정식의 그래프는 평행선의 한 쌍입니다.

두 개의 방정식이 모두 일치하더라도 세 개의 선형 방정식이 일치하지 않을 수 있습니다.예를 들면, 방정식들은

${\displaystyle {\begin{alignat}{7}x&;+\y&;=\&1&\2x&;+\y&;=\3x&;+&2y&;=\&3&\end{alignat}}$

일정하지 않은처음 두 개의 방정식을 더하면 3x + 2y = 2가 되며, 이는 세 번째 방정식에서 차감되어 0 = 1이 됩니다.이들 방정식 중 어느 두 개라도 공통적인 해를 가지고 있습니다.동일한 현상은 방정식의 개수에 상관없이 발생할 수 있습니다.

일반적으로 시스템에서 방정식의 왼쪽이 선형 종속이고 상수 항이 종속 관계를 만족하지 않으면 불일치가 발생합니다.좌변이 선형으로 독립된 방정식 체계는 항상 일관됩니다.

다른 말로 하면, 루체-카펠리 정리에 따르면, 증강 행렬의 순위가 계수 행렬의 순위보다 크면 어떤 방정식 체계(과다 결정되었거나 다른 방식)도 일관되지 않습니다.반면에 이 두 행렬의 순위가 같으면 시스템에 적어도 하나의 해가 있어야 합니다.순위가 변수의 수와 같은 경우에만 유일한 솔루션입니다.그렇지 않으면 일반적인 해는 k개의 자유 매개변수를 가지며, k는 변수의 수와 순위 사이의 차이입니다. 따라서 이러한 경우에는 해가 무한히 존재합니다.방정식 체계의 순위(즉, 증강 행렬의 순위)는 [변수의 수] + 1보다 결코 높을 수 없으며, 이는 방정식의 수가 얼마든지 있는 시스템은 항상 [변수의 수] + 1과 같은 수의 독립적인 방정식을 가진 시스템으로 축소될 수 있음을 의미합니다.

동치

두 번째 시스템의 각 방정식이 첫 번째 시스템의 방정식에서 대수적으로 도출될 수 있다면 동일한 변수 집합을 사용하는 두 개의 선형 시스템은 동등합니다.두 시스템이 모두 일치하지 않거나 각 시스템의 방정식이 다른 시스템의 방정식의 선형 조합일 경우 두 시스템은 동등합니다.두 선형 시스템이 동일한 해 집합을 갖는 경우와 동일한 경우에만 두 선형 시스템이 동등하다는 것을 알 수 있습니다.

선형 시스템 해결

선형 방정식 체계를 풀기 위한 몇 가지 알고리즘이 있습니다.

솔루션 설명

해 집합이 유한한 경우에는 단일 원소로 줄어듭니다.이 경우, 독특한 해는 왼쪽이 미지수의 이름이고 오른쪽이 해당 값인 방정식의 연속으로 설명됩니다. 예를 들어$$(${\displaystyle x}$ = ${\displaystyle 3,}$ y${\displaystyle }$=$$- 2, z = 6 ) {\displaystyle (x = 3,\;y = - 2,\;z = 6)}.예를 들어, 알 수 없는 것에 대한 순서가 고정된 경우, 해는 앞의 예에서$$ (${\displaystyle 3,}$ ${\displaystyle -2\mathrm{},}$ 6$){\displaystyle$ ($3,\,$ - 2$,\, 6)}$와 같이 값의 벡터로 설명될 수 있습니다.

해가 무한히 많은 집합을 설명하려면 일반적으로 변수 중 일부를 자유 변수(또는 독립 변수 또는 매개 변수)로 지정합니다. 즉, 나머지 변수는 자유 변수의 값에 종속적입니다.

예를 들어 다음과 같은 시스템을 생각해 보겠습니다.

${\displaystyle {\begin{alignat}{7}x&+\&&&-&&&2z&=\&3x&+&+&6z&=\&end{alignat}}$

이 시스템에 설정된 해는 다음 식으로 설명할 수 있습니다.

${\displaystyle x=-7z-1\;\;\;\;{\text{and}}\;\;\;y=3z+2{\text{.}}$

여기서 z는 자유 변수이고 x와 y는 z에 종속됩니다.해 집합의 모든 점은 먼저 z 값을 선택한 다음 x와 y에 해당하는 값을 계산하여 얻을 수 있습니다.

각 자유 변수는 해 공간에 1개의 자유도를 제공하며, 그 수는 해 집합의 차원과 동일합니다.예를 들어, 해 집합의 한 점은 모수 z의 값을 지정하여 선택할 수 있으므로, 위의 식에 대한 해 집합은 선이 됩니다.고차수의 무한해는 평면 또는 고차수 집합을 설명할 수 있습니다.

자유 변수에 대한 선택이 다르면 동일한 솔루션 집합에 대한 설명이 다를 수 있습니다.예를 들어, 위의 방정식에 대한 해는 다음과 같이 나타낼 수 있습니다.

${\displaystyle y=-{\frac {3}{7}}x+{\frac {11}{7}}\;\;\;\;\;{\text{and}}\;\;z=-{\frac {1}{7}x-{\frac {1}{7}}{\text{.}}$

여기서 x는 자유 변수이고 y와 z는 종속적입니다.

변수제거

선형 방정식 체계를 푸는 가장 간단한 방법은 변수를 반복적으로 제거하는 것입니다.이 방법은 다음과 같이 설명할 수 있습니다.

1. 첫 번째 방정식에서 변수 중 하나에 대해 다른 변수의 항으로 풀이합니다.
2. 이 식을 나머지 방정식에 대입합니다.이것은 방정식이 하나 적고 알려지지 않은 방정식 체계를 만듭니다.
3. 시스템이 단일 선형 방정식으로 축소될 때까지 1단계와 2단계를 반복합니다.
4. 이 식을 풀고 전체 해를 찾을 때까지 다시 대입합니다.

예를 들어 다음과 같은 시스템을 생각해 보겠습니다.

${\displaystyle {\begin{case}x+3y-2z=5\\3x+5y+6z=7\2x+4y+3z=8\end{case}}$

x에 대한 첫 번째 방정식을 풀면 x = 5 + 2z - 3y가 되고 이것을 두 번째와 세 번째 방정식에 연결하면 산출됩니다.

${\displaystyle {\begin{case}y=3z+2\y={\tfrac {7}{2}}z+1\end{case}}$

이 두 방정식의 LHS는 동일하므로 방정식의 RHS를 동일시합니다.이제 다음과 같은 기능이 있습니다.

${\displaystyle {\begin{aligned}3z+2={\tfrac {7}{2}z+1\\\\rightarrow z=2\end{aligned}}$

두 번째 또는 세 번째 방정식에 z = 2를 대입하면 y = 8이 되고, 첫 번째 방정식에 y와 z의 값을 대입하면 x = -15가 됩니다.따라서 해 집합은 순서가 매겨진 삼중 (${\displaystyle x,}$ y${\displaystyle ,}$ ${\displaystyle z}$ )${\displaystyle }$=${\displaystyle }$(${\displaystyle }$- 15$,$ 8, 2 ) {\displaystyle (x,y,z) = (-15,8,2)}입니다.

행축소

행 감소(가우시안 소거라고도 함)에서, 선형 시스템은 증강 매트릭스로서^[7] 표현됩니다.

${\displaystyle \left[{\begin{array}{rrrr}1&3&-2&5\\3&5&6&7\2&4&8\end{array}}\right]{\text{.}}$

그런 다음 이 행렬은 기본 행 연산을 사용하여 감소된 행 에클론 형태에 도달할 때까지 수정됩니다.기본 행 작업에는 세 가지 유형이 있습니다.^[7]

유형 1: 두 행의 위치를 맞춥니다.

유형 2: 행에 0이 아닌 스칼라를 곱합니다.

유형 3: 한 행에 다른 행의 스칼라 배수를 더합니다.

이러한 연산은 가역적이기 때문에 생성된 증강 매트릭스는 항상 원본과 동일한 선형 시스템을 나타냅니다.

증강 행렬을 행으로 줄이기 위한 몇 가지 특정 알고리즘이 있는데, 그 중 가장 간단한 것은 가우스 제거와 가우스-조르단 제거입니다.다음 계산은 위의 행렬에 적용된 가우스-요르단 제거를 보여줍니다.

${\displaystyle {\begin{aligned}\left[{\begin{array}{rrrr}1&-2&5\\\3&5&6&7\2&4&3&8\end{array}}\right]&\sim \left[{\begin{array}{rrrr}1&-2&5\0&-4&12&8\end{array}}\right]\sim \left[{\begin{array}{rrr}r1&3&2&5\0&-4&12&-8\0&-2&7&2\end{array}}\right]\sim \left[{\begin{array}{rrrrr}1&-2&5\0&1&3&2\end{array}}\right]\sim \left[{\{{array}{rrrr}1&2&5\0&2&7&2\end{array}}\right]\&\sim \left[{\begin{array}{rrrr}1&-2&5\\\0&1&-3&2\end{array}}\right]\sim \left[{\begin{array}{rrrr}1&3&-2&5\0&1&8\0&0&1&2\end{array}}\right]\sim \left[{\begin{array}{rrrr}1&3&9\0&0&8\0&1&2\end{array}}\right]\sim \left[{\begin{array}{rrrrr}1&0&-15\0&1&2\end{array}}\right]\sim \left[{\{{array}{rrrrr}1&0&0&1&8\0&1&2\end{array}}\right].\end{aligned}}$

마지막 행렬은 감소된 행 에켈론 형태이고 계 x = -15, y = 8, z = 2를 나타냅니다. 변수의 대수적 제거에 대한 이전 절의 예와 비교하면 이 두 방법은 사실 동일합니다. 그 차이는 계산이 어떻게 기록되는지에 있습니다.

크라머의 법칙

크레이머의 법칙은 선형 방정식 체계의 해에 대한 명시적인 공식이며, 각 변수는 두 개의 결정 인자의 몫으로 주어집니다.^[8]예를 들어, 시스템에 대한 해결책은

${\displaystyle {\begin{alignat}{7}x&;+&;3y&;-&\;2z&;=&;5\3x&;+&;5y&;+&;6z&;=&;7\2x&;+&;4y&;=&;8\end{alignat}}$

에 의해 주어집니다.

${\displaystyle x={\frac {\,{\begin{vmatrix}5&-2\\7&5&6\8&4&3\end{vmatrix}}\,}{\,{\begin{vmatrix}1&3&-2\3&5&6\2&4&3\end{vmatrix}\,},\;\;\;y={\frac {\,{\begin{vmatrix}1&5&-2\3&6\2&8&3\end{vmatrix},}{,{\begin{vmatrix}1&3&2\3&6\2&4&3\end{vmatrix}},\;\;\;z={\frac {,{\begin{vmatrix}1&3&5\3&7\2&8\end{vmatrix}},}{,{\beg{vmatrix}1&2\,}{,{\{i}n{vmatrix}1&3&-2\3&5&6\2&4&3\end{vmatrix}\,}}.}$

각 변수에 대해 분모는 계수 행렬의 행렬식이고 분자는 한 열이 상수 항 벡터로 대체된 행렬의 행렬식입니다.

크레이머의 규칙은 이론적으로 중요하지만, 큰 행렬에 대한 실용적인 가치는 거의 없습니다. 큰 행렬식의 계산은 다소 번거롭기 때문입니다.실제로 큰 행렬식은 행 감소를 사용하여 가장 쉽게 계산됩니다.또한 Cramer의 규칙은 수치 특성이 매우 좋지 않아 연산을 무한한 정밀도로 합리적인 산술로 수행하지 않는 한 작은 시스템도 안정적으로 해결하기에 적합하지 않습니다.^[9]

행렬해

방정식 체계를 행렬 형태 A ${\displaystyle x}$ = ${\displaystyle b}$ ${\$displaystyle A\mathbf {x} =\mathbf {b} }로 표현하면 전체 해 집합도 행렬 형태로 표현할 수 있습니다.만약 행렬 A가 정사각형이고 (m개의 행과 n=m개의 열이 있음), 그리고 완전한 순위를 가지면 (모든 m개의 행은 독립적임), 시스템은 다음과 같이 주어진 유일한 해를 갖습니다.

${\displaystyle \mathbf {x} = A^{-1}\mathbf {b} }$

여기서 $A{\displaystyle {}^{}}$ -${\displaystyle 1^{}}$ ${\$는 A의 역입니다.일반적으로, m=n 여부에 관계없이, 그리고 A의 순위에 관계없이, 모든 해(존재하는 경우)는${\displaystyle {}^{}}A$ + ${\displaystyle$ A$^{+}}$로 표시되는 $A$의 무어-펜로즈 역을 사용하여 다음과 같이 주어집니다$.$

${\displaystyle \mathbf {x} = A^{+}\mathbf {b} +\left(I-A^{+}A\right)\mathbf {w} }$

여기서 $w{\displaystyle \mathbf{}}$ ${\$은 가능한 모든 nx1 벡터에 걸쳐 있는 자유 매개 변수 벡터입니다.임의의 해가 존재하기 위한 $필요충분조건$은 ${\displaystyle w}$ =$$0 {\$displaystyle$ \$mathbf {$w} =\$mathbf$ {0$}$을 사용하여 구한 퍼텐셜해가 A x = b {\displaystyle A\mathbf {x} =\mathbf {b} }, 즉 A + b = b를 만족하는 것입니다. {\displaystyle AA^{+}\mathbf {b} =\mathbf {b} 이 조건이 성립하지 않으면,방정식 체계가 일관성이 없고 해가 없습니다.이 상태가 지속되면 시스템이 일관되고 솔루션이 하나 이상 존재합니다.예를 들어, A가 정사각형이고 전체 순위인 위의 경우, $A{\displaystyle {}^{}}$+ ${\$는 단순히$$ $A{\displaystyle {}^{}}$ -${\displaystyle 1^{}}$ ${\$와 같으며$$, 일반적인 해 방정식은 다음과 같이 단순화됩니다.

${\displaystyle \mathbf {x} =A^{-1}\mathbf {b} +\left(I-A^{-1}A\right)\mathbf {w} =A^{-1}\mathbf {b} +\left(I-I\right)\mathbf {w} =A^{-1}\mathbf {b} }$

앞에서 설명한 바와 같이, $w{\displaystyle \mathbf{}}$ ${\$가) 해에서 완전히 탈락하여$$ 하나의 해만 남게 되었습니다.그러나 다른 경우에는 $w{\displaystyle \mathbf{}}$ ${\$가) 남아$$ 있으므로 자유 매개 변수 $벡터{\displaystyle \mathbf{}}$ w ${\$의 무한한 전위 값이 방정식의$$ 해를 제공합니다.

기타방법

서너 개 방정식의 시스템은 손으로 쉽게 풀 수 있지만(크라코비안 참조), 컴퓨터는 종종 더 큰 시스템에 사용됩니다.선형 방정식 체계를 풀기 위한 표준 알고리즘은 약간의 수정을 통해 가우스 제거를 기반으로 합니다.첫째, 결과가 부정확해질 수 있는 작은 숫자로 나누는 것을 피하는 것이 중요합니다.이 작업은 필요한 경우 방정식의 순서를 바꾸어서 수행할 수 있으며, 이를 피벗이라고 합니다.둘째, 알고리즘은 정확히 가우스 제거를 하지는 않지만 행렬 A의 LU 분해를 계산합니다.이것은 대부분 조직적인 도구이지만, 행렬 A는 같지만 벡터 b는 다른 여러 시스템을 해결해야 한다면 훨씬 더 빠릅니다.

행렬 A가 어떤 특별한 구조를 가지고 있다면, 이것을 이용하여 더 빠르거나 더 정확한 알고리즘을 얻을 수 있습니다.예를 들어, 대칭적인 양의 정행렬을 갖는 시스템은 촐레스키 분해로 두 배 빠르게 해결할 수 있습니다.레빈슨 재귀는 토플리츠 행렬의 빠른 방법입니다.응용 프로그램에서 자주 나타나는 영 원소(소위 희소 행렬)가 많은 행렬에 대해서도 특별한 방법이 있습니다.

매우 큰 시스템의 경우에는 완전히 다른 접근 방식을 사용하는 경우가 많은데, 그렇지 않으면 시간이나 메모리가 너무 많이 소요됩니다.이 아이디어는 솔루션에 대한 초기 근사치로 시작하여(정확할 필요는 전혀 없음), 몇 단계에 걸쳐 이 근사치를 변경하여 실제 솔루션에 더 가깝게 만드는 것입니다.근사치가 충분히 정확해지면 이것이 시스템에 대한 해결책으로 간주됩니다.이것은 반복적인 방법의 클래스로 이어집니다.일부 희소 행렬의 경우 무작위성을 도입하면 반복 방법의 속도가 향상됩니다.^[10]

방정식의 선형 시스템을 위한 양자 알고리즘도 있습니다.^[11]

동차계

모든 상수항이 0인 경우 선형 방정식 체계는 균질합니다.

${\displaystyle {\begin{alignat}{7}a_{11}x_{1}&+\&a_{12}x_{2}&+\cdots +\&a_{1n}x_{1n}&=\&&&a_{21}x_{1}&+\cdots +\&a_{2}x_{n}&=\&a_{m1}x_{1}&+\cdots +\cdots +\n}x_{m2}x_{n}&=\cdots +\n0.\\\\end{alignat}}}$

균질 시스템은 다음과 같은 형태의 행렬 방정식과 같습니다.

${\displaystyle A\mathbf {x} =\mathbf {0}}$

여기서 A는 m × n 행렬이고, x는 n개의 원소를 갖는 열 벡터이고, 0은 m개의 원소를 갖는 영 벡터입니다.

균질 솔루션 집합

모든 균질한 시스템은 각 변수에 0의 값을 할당함으로써 얻을 수 있는 0(또는 사소한) 솔루션으로 알려진 적어도 하나의 솔루션을 가지고 있습니다.시스템에 비단수 행렬(det(A) ≠ 0)이 있는 경우 유일한 솔루션이기도 합니다.시스템에 단수 행렬이 존재하는 경우, 무한한 수의 해를 갖는 해 집합이 존재합니다.이 솔루션 집합에는 다음과 같은 추가 속성이 있습니다.

1. 만약 u와 v가 동차계의 해를 나타내는 두 벡터라면, 벡터 합 u + v도 동차계의 해가 됩니다.
2. 만약 u가 균질한 계에 대한 해를 나타내는 벡터이고, r이 임의의 스칼라라면, ru는 또한 계에 대한 해입니다.

해 집합이 R의ⁿ 선형 부분 공간이 되는 데 필요한 속성입니다.특히, 균질 시스템으로 설정된 해는 해당 행렬 A의 널 스페이스와 같습니다.

비균질 시스템과의 관계

선형 시스템에 대한 솔루션과 해당 동종 시스템에 대한 솔루션 사이에는 밀접한 관계가 있습니다.

${\displaystyle A\mathbf {x} =\mathbf {b} \qquad {\text{and}}\qquad A\mathbf {x} =\mathbf {0} .}$

구체적으로, p가 선형 시스템 Ax = b에 대한 임의의 특정 해일 경우, 전체 해 집합은 다음과 같이 나타낼 수 있습니다.

${\displaystyle \left\{\mathbf {p} +\mathbf {v} :\mathbf {v} {\text{는 }}에 대한 임의의 솔루션입니다. A\mathbf {x} =\mathbf {0} \right\}}$

기하학적으로, 이것은 Ax = b에 대한 해 집합이 Ax = 0에 대한 해 집합의 번역임을 의미합니다. 구체적으로, 첫 번째 계에 대한 평탄은 균질한 계에 대한 선형 부분공간을 벡터 p에 의해 번역함으로써 구할 수 있습니다.

이 추론은 시스템 Ax = b에 적어도 하나의 솔루션이 있는 경우에만 적용됩니다.이것은 벡터 b가 선형 변환 A의 이미지에 있는 경우에만 발생합니다.

참고 항목

참고문헌

서지학

• Anton, Howard (1987), Elementary Linear Algebra (5th ed.), New York: Wiley, ISBN 0-471-84819-0
• Beauregard, Raymond A.; Fraleigh, John B. (1973), A First Course In Linear Algebra: with Optional Introduction to Groups, Rings, and Fields, Boston: Houghton Mifflin Company, ISBN 0-395-14017-X
• Burden, Richard L.; Faires, J. Douglas (1993), Numerical Analysis (5th ed.), Boston: Prindle, Weber and Schmidt, ISBN 0-534-93219-3
• Cullen, Charles G. (1990), Matrices and Linear Transformations, MA: Dover, ISBN 978-0-486-66328-9
• Golub, Gene H.; Van Loan, Charles F. (1996), Matrix Computations (3rd ed.), Baltimore: Johns Hopkins University Press, ISBN 0-8018-5414-8
• Harper, Charlie (1976), Introduction to Mathematical Physics, New Jersey: Prentice-Hall, ISBN 0-13-487538-9
• Harrow, Aram W.; Hassidim, Avinatan; Lloyd, Seth (2009), "Quantum Algorithm for Linear Systems of Equations", Physical Review Letters, 103 (15), doi:10.48550/arXiv.0811.3171
• Sterling, Mary J. (2009), Linear Algebra for Dummies, Indianapolis, Indiana: Wiley, ISBN 978-0-470-43090-3
• Whitelaw, T. A. (1991), Introduction to Linear Algebra (2nd ed.), CRC Press, ISBN 0-7514-0159-5

추가열람

• Axler, Sheldon Jay (1997), Linear Algebra Done Right (2nd ed.), Springer-Verlag, ISBN 0-387-98259-0
• Lay, David C. (August 22, 2005), Linear Algebra and Its Applications (3rd ed.), Addison Wesley, ISBN 978-0-321-28713-7
• Meyer, Carl D. (February 15, 2001), Matrix Analysis and Applied Linear Algebra, Society for Industrial and Applied Mathematics (SIAM), ISBN 978-0-89871-454-8, archived from the original on March 1, 2001
• Poole, David (2006), Linear Algebra: A Modern Introduction (2nd ed.), Brooks/Cole, ISBN 0-534-99845-3
• Anton, Howard (2005), Elementary Linear Algebra (Applications Version) (9th ed.), Wiley International
• Leon, Steven J. (2006), Linear Algebra With Applications (7th ed.), Pearson Prentice Hall
• Strang, Gilbert (2005), Linear Algebra and Its Applications

외부 링크

• Wikimedia Commons의 선형방정식 체계 관련 매체