인터랙션 네트

상호작용 그물은 선형 논리의 증명 구조의 일반화로서 1990년에^[1] 이브 라퐁이 고안한 연산의 그래픽 모델이다.상호 작용 네트워크 시스템은 에이전트 유형 집합과 상호 작용 규칙 집합으로 지정된다.상호작용 네트는 상호 작용망의 많은 부분에서 동시에 연산이 일어날 수 있고 동기화가 필요하지 않다는 점에서 본질적으로 분산된 연산 모델이다.후자는 이 연산 모델에서 감소하는 강한 결합 속성에 의해 보장된다.그러므로 상호 작용 그물은 거대한 병렬주의를 위한 자연적인 언어를 제공한다.상호작용 그물은 효율적인 폐쇄 감소와^[2] 최적화와 같은 람다 미적분학의 많은 구현의 핵심에 있다.^[3]

정의들

상호작용망은 작용제와 가장자리로 구성된 그래프와 같은 구조물이다.

$\alpha$ ${\$ $displaystyle$ $\alpha }$ 유형의 에이전트와 $\alpha$ arity ${\text{ar}}(\alpha )=n\geq 0$ ) ${\text{ar}}(\alpha )=n\geq 0$ = ${\text{ar}}(\alpha )=n\geq 0$ ${\text{ar}}(\alpha )=n\geq 0$ ${\text{ar}}(\alpha )=n\geq 0$ ${\displaystyle {\text{ar}}(\alpha$ )= $\geq$ 0 $}$ 의 $n$ 보조 포트가 하나씩 있는 ${\text{ar}}(\alpha )=n\geq 0$ 경우.어떤 포트라도 최대 한 에지에 연결할 수 있다.어떤 에지에 연결되지 않은 포트를 free port라고 한다.자유 포트는 상호 작용 네트워크의 인터페이스를 형성한다.모든 에이전트 유형은 시그니처라고 하는 $\Sigma$ $\Sigma$ $\Sigma$ 집합에 속한다.

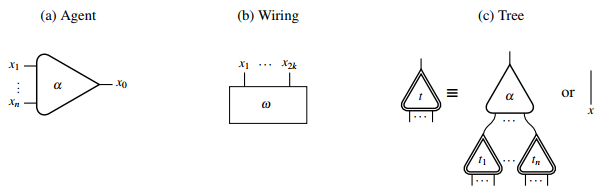
엣지만으로 구성된 상호 작용망을 배선이라고 하며 일반적으로 $\omega$ $\omega$ 로 표시한다 $\omega$ $루트$ x가{\ $displaystyle x$ }인 $t$ $트리$ t ${\displaystyt t}$ 은(는) $에지$ x{\ $displaysty x$ 또는 에이전트 $\alpha$ {\ $displaystylepha }($ 자유형 $\alpha$ 포트)로 귀납적으로 정의된다 $x$ . $x$ ${\$ $displaystyle$ $x}$ 및 $x$ 그 보조 포트 x $x_{i}$ ${\$ $x_{i}}$ 이(가) 다른 나무 $t_{i}$ 의 뿌리에 연결됨 $x_{i}$ $t_{i}$

그래픽으로 상호작용 그물의 원시 구조는 다음과 같이 나타낼 수 있다.

두 에이전트가 서로 주 포트와 연결되면 활성 쌍을 형성한다.활성 쌍의 경우 활성 쌍이 다른 상호 작용 네트에 다시 쓰는 방법을 설명하는 상호 작용 규칙을 도입할 수 있다.활성 쌍이 없는 상호작용 그물은 정상적인 형태라고 한다. $\Sigma$ signature ${\displaystyle \Sigma }($ ${\text{ar}}:\Sigma \rightarrow \mathbb {N}$ : ${\text{ar}}:\Sigma \rightarrow \mathbb {N}$ → N ${\$ $\Sigma \rigarrow \righ$ \mathb { $N}$ 정의 ${\text{ar}}:\Sigma \rightarrow \mathbb {N}$ )와 함께 $\alpha \in \Sigma$ $\alpha \in \Sigma$ ∈ $\alpha \in \Sigma$ $\alpha \in \Sigma$ 에 대해 정의된 일련의 상호 작용 규칙이 상호 $\alpha \in \Sigma$ 작용 시스템을 구성한다.

교호작용 미적분학

상호작용망의 텍스트 표현은 상호작용 미적분학이라고^[4] 불리며 프로그래밍 언어로 볼 수 있다.

유도적으로 정의된 트리는 상호작용 미적분학에서 $t::=\alpha (t_{1},\dots ,t_{n})\ |\ x$ $t::=\alpha (t_{1},\dots ,t_{n})\ |\ x$ $t::=\alpha (t_{1},\dots ,t_{n})\ |\ x$ $t::=\alpha (t_{1},\dots ,t_{n})\ |\ x$ $t::=\alpha (t_{1},\dots ,t_{n})\ |\ x$ , $t::=\alpha (t_{1},\dots ,t_{n})\ |\ x$ … $t::=\alpha (t_{1},\dots ,t_{n})\ |\ x$ , $t::=\alpha (t_{1},\dots ,t_{n})\ |\ x$ $t::=\alpha (t_{1},\dots ,t_{n})\ |\ x$ ) x ${\displaystyle t::=\alpha(t_{1},\dots ,t_{n}\ x$ }\ x $}$ 에 해당하며 $,$ $x$ 서 $x$ x는이름이라고 $한다$ .

모든 상호 작용 $네트$ N{\ $displaystyle N$ }은(는) 다음과 같이 이전에 정의된 배선 및 트리 원시 요소를 사용하여 다시 그릴 $N$ 수 있다.

교호작용에서 미적분학은 구성에 해당한다.

$c\equiv \langle t_{1},\dots ,t_{m}\ |\ v_{1}=w_{1},\dots ,v_{n}=w_{n}\rangle$ $c\equiv \langle t_{1},\dots ,t_{m}\ |\ v_{1}=w_{1},\dots ,v_{n}=w_{n}\rangle$ $c\equiv \langle t_{1},\dots ,t_{m}\ |\ v_{1}=w_{1},\dots ,v_{n}=w_{n}\rangle$ $c\equiv \langle t_{1},\dots ,t_{m}\ |\ v_{1}=w_{1},\dots ,v_{n}=w_{n}\rangle$ $c\equiv \langle t_{1},\dots ,t_{m}\ |\ v_{1}=w_{1},\dots ,v_{n}=w_{n}\rangle$ , $c\equiv \langle t_{1},\dots ,t_{m}\ |\ v_{1}=w_{1},\dots ,v_{n}=w_{n}\rangle$ … $c\equiv \langle t_{1},\dots ,t_{m}\ |\ v_{1}=w_{1},\dots ,v_{n}=w_{n}\rangle$ , $c\equiv \langle t_{1},\dots ,t_{m}\ |\ v_{1}=w_{1},\dots ,v_{n}=w_{n}\rangle$ $c\equiv \langle t_{1},\dots ,t_{m}\ |\ v_{1}=w_{1},\dots ,v_{n}=w_{n}\rangle$ v $c\equiv \langle t_{1},\dots ,t_{m}\ |\ v_{1}=w_{1},\dots ,v_{n}=w_{n}\rangle$ = $c\equiv \langle t_{1},\dots ,t_{m}\ |\ v_{1}=w_{1},\dots ,v_{n}=w_{n}\rangle$ 1 $c\equiv \langle t_{1},\dots ,t_{m}\ |\ v_{1}=w_{1},\dots ,v_{n}=w_{n}\rangle$ , $c\equiv \langle t_{1},\dots ,t_{m}\ |\ v_{1}=w_{1},\dots ,v_{n}=w_{n}\rangle$ … $c\equiv \langle t_{1},\dots ,t_{m}\ |\ v_{1}=w_{1},\dots ,v_{n}=w_{n}\rangle$ , $c\equiv \langle t_{1},\dots ,t_{m}\ |\ v_{1}=w_{1},\dots ,v_{n}=w_{n}\rangle$ $c\equiv \langle t_{1},\dots ,t_{m}\ |\ v_{1}=w_{1},\dots ,v_{n}=w_{n}\rangle$ = w $c\equiv \langle t_{1},\dots ,t_{m}\ |\ v_{1}=w_{1},\dots ,v_{n}=w_{n}\rangle$ $c\equiv \langle t_{1},\dots ,t_{m}\ |\ v_{1}=w_{1},\dots ,v_{n}=w_{n}\rangle$ ${\displaystyle c\equiv \langle t_{1},\clangle ,t_{m}\\ \ v_n1}=w_{n$ .

여기서 $t_{i}$ $t_{i}$ ${\$ v $v_{i}$ ${\$ w $w_{i}$ ${\$ 는 임의의 용어다 $w_{i}$ .왼쪽의 $t_{1},...,t_{m}$ 순서 $t_{1},...,t_{m}$ $t_{1},...,t_{m}$ , $t_{1},...,t_{m}$ . $t_{1},...,t_{m}$ . . . $t_{1},...,t_{m}$ $t_{1},...,t_{m}$ ${\$ }, $..., t_{m}}$ 을(를) 인터페이스라고 하며, 오른쪽에는 $v_{i}=w_{i}$ $v_{i}=w_{i}$ $v_{i}=w_{i}$ = $v_{i}=w_{i}$ ${\$ $displaystyle$ $v_{i}=w_$ ${$ $i}}}}$ 의 순서가 없는 다중 집합이 포함되어 있다 $.$ 배선 $\omega$ 은 이름으로 번역되며 $\omega$ , 각 이름은 $ex$ 가 발생한다.한 구성에서 두 번 연기한다.

$\lambda$ $\lambda$ - 미적분학에서와 $\lambda$ 마찬가지로 상호작용 미적분학에는 $\alpha$ ${\displaystyle \alpha$ } -변환 $\alpha$ 및 치환 개념이 구성에 자연스럽게 정의되어 있다.구체적으로 어떤 이름의 두 발생 모두 지정된 구성에서 발생하지 않는 경우 새 이름으로 대체할 수 있다.구성은 $\alpha$ $\alpha$ -전환까지 $\alpha$ 동등한 것으로 간주된다. $즉$ , 대체 $t[x:=u]$ [ $t[x:=u]$ $t[x:=u]$ $u$ $t$ 에서 x ${\$ $displaystyle$ t $}$ 이(가 $)$ t ${\displaystyle$ $x$ $t$ 이라는 용어에 정확히 $x$ 한 개의 발생이 있는 경우 $u$ $t$ ${\displaystyle$ $u$ $}$ 이라는 용어의 $x$ $x$ ${\displaystystyle$ x $}$ 을 다른 $u$ 로 바꾼 $t$ 결과인 $t[x:=u]$ 것이다.

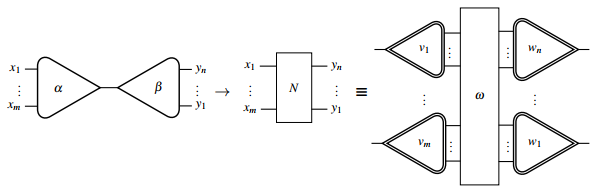
모든 상호작용 규칙은 다음과 같이 그래픽으로 나타낼 수 있다.

where $\alpha ,\beta \in \Sigma$ , and the interaction net $N$ on the right-hand side is redrawn using the wiring and tree primitives in order to translate into the interaction calculus as $\alpha [v_{1},\dots ,v_{m$ $]\bowtie \beta [w_{1},\dots,w_{n$

상호작용 미적분학은 상호작용 네트에 정의된 그래프 재작성에서 볼 수 있는 것보다 더 상세한 구성의 감소를 정의한다.즉, $\alpha [v_{1},\dots ,v_{m}]\bowtie \beta [w_{1},\dots ,w_{n}]$ [ $\alpha [v_{1},\dots ,v_{m}]\bowtie \beta [w_{1},\dots ,w_{n}]$ 1 $\alpha [v_{1},\dots ,v_{m}]\bowtie \beta [w_{1},\dots ,w_{n}]$ , $\alpha [v_{1},\dots ,v_{m}]\bowtie \beta [w_{1},\dots ,w_{n}]$ … , $\alpha [v_{1},\dots ,v_{m}]\bowtie \beta [w_{1},\dots ,w_{n}]$ v $\alpha [v_{1},\dots ,v_{m}]\bowtie \beta [w_{1},\dots ,w_{n}]$ $\alpha [v_{1},\dots ,v_{m}]\bowtie \beta [w_{1},\dots ,w_{n}]$ $\alpha [v_{1},\dots ,v_{m}]\bowtie \beta [w_{1},\dots ,w_{n}]$ $\alpha [v_{1},\dots ,v_{m}]\bowtie \beta [w_{1},\dots ,w_{n}]$ , $\alpha [v_{1},\dots ,v_{m}]\bowtie \beta [w_{1},\dots ,w_{n}]$ … , $\alpha [v_{1},\dots ,v_{m}]\bowtie \beta [w_{1},\dots ,w_{n}]$ $\alpha [v_{1},\dots ,v_{m}]\bowtie \beta [w_{1},\dots ,w_{n}]$ ${\displaystyle \alpha [v_{1},\dots ,v_{m}]\bowtie \beta [w_{1},\dots ,w_{n$ 다음과 같은 감소가 가능하다.

$\langle {\vec {t}}\ \ \alpha (t_{1},\dots ,t_{m})=\beta (u_{1},\dots ,u_{n}),\Delta \rangle \rightarrow \langle {\vec {t}}\ \ t_{1}=v_{1},\dots ,t_{m}=v_{m},u_{1}=w_{1},\dots ,u_{n}=w_{n},\Delta \rangle$

상호 작용이라고 불린다.방정식 중 $x=u$ 가 $x=u$ x = $x=u$ {\ $displaystyle$ x= $u}$ 의 형태를 갖는 경우 $x=u$ 어떤 $용어$ t{\ $displaystyle t}$ 에서 $x$ x{\ $displaystyle x}$ 의 다른 발생을 대체하여 양방향으로 적용할 수 있다 $t$

$\langle \dots t\dots \ \ x=u,\Delta \rangle \rightarrow \langle \dots t[x:=u]\dots \ \ \Delta \rangle$ or ${\displaystyle \langle {\vec {t}}\ \ x=u,t=w,\Delta \rangle \righ$ $tarrow \langle {\vec{t}\\ t[x:=u]=w,\Delta \angle$ $\langle {\vec {t}}\ |\ x=u,t=w,\Delta \rangle \rightarrow \langle {\vec {t}}\ |\ t[x:=u]=w,\Delta \rangle$

$x$ $x=t$ = $x=t$ ${\displaystyle$ x $=t$ $}$ 방정식이 $t$ $t$ 에서 발생하면 $x$ 교착 $x=t$ 상태라고 하며, 일반적으로 교착 상태가 없는 상호 작용 그물만 고려한다 $t$ 상호 작용과 양방향은 함께 구성에 대한 감소 관계를 정의한다.구성 $c$ $c$ 이(가) 방정식이 남아 있지 않은 정상적인 $c'$ 형식 $c$ $'$ ${\$ 으로 감소한다는 $c$ 사실은 $c\downarrow c'$ $c\downarrow c'$ c $c\downarrow c'$ ′ ′ ${\$ c $\downarrow$ c $'}$ 로 표시된다 $c\downarrow c'$

특성.

상호작용 네트는 다음과 같은 특성에서 이익을 얻는다.

지역성(활성 쌍만 다시 쓸 수 있음)
선형성(각 교호작용 규칙을 일정한 시간에 적용할 수 있음);
strong confluence also known as one-step diamond property (if $c\rightarrow c_{1}$ and $c\rightarrow c_{2}$ , then $c_{1}\rightarrow c'$ and $c_{2}\rightarrow c'$ for some $c'$ ).

이 특성들은 함께 거대한 병렬 처리를 가능하게 한다.

상호작용 결합기

다른 상호작용 시스템을 시뮬레이션할 수 있는 가장 간단한 상호작용 시스템 중 하나는 상호작용 결합기 시스템이다.^[5]Its signature is $\Sigma =\{\epsilon ,\delta ,\gamma \}$ with ${\text{ar}}(\epsilon )=0$ and ${\text{ar}}(\delta )={\text{ar}}(\gamma )=2$ . Interaction rules for these agents are:

$\epsilon \bowtie \alpha [\epsilon ,\dots ,\epsilon ]$ [ $\epsilon \bowtie \alpha [\epsilon ,\dots ,\epsilon ]$ , … $\epsilon \bowtie \alpha [\epsilon ,\dots ,\epsilon ]$ $\epsilon \bowtie \alpha [\epsilon ,\dots ,\epsilon ]$ ${\displaystyle \epsilon \bowtie$ \ $\[\epsilon ,\epsilon ]}$ 지우기라고 함 $\epsilon \bowtie \alpha [\epsilon ,\dots ,\epsilon ]$ ;
$\delta [\alpha (x_{1},\dots ,x_{n}),\alpha (y_{1},\dots ,y_{n})]\bowtie \alpha [\delta (x_{1},y_{1}),\dots ,\delta (x_{n},y_{n})]$ called duplication;
$\delta [x,y]\bowtie \delta [x,y]$ [ $\delta [x,y]\bowtie \delta [x,y]$ , $\delta [x,y]\bowtie \delta [x,y]$ $\delta [x,y]\bowtie \delta [x,y]$ [ x $\delta [x,y]\bowtie \delta [x,y]$ , y $\delta [x,y]\bowtie \delta [x,y]$ Δ [ $\delta [x,y]\bowtie \delta [x,y]$ , y $]$ {\ $displaystyle \x [x,$ y $\delta [x,y]\bowtie \delta [x,y]$ ]\bowty $\tie [$ x, $\gamma [x,y]\bowtie \gamma [y,x]$ $\gamma [x,y]\bowtie \gamma [y,x]$ [ $,y$ δ $[\displaysty$ sty $\$ gamma $[x$

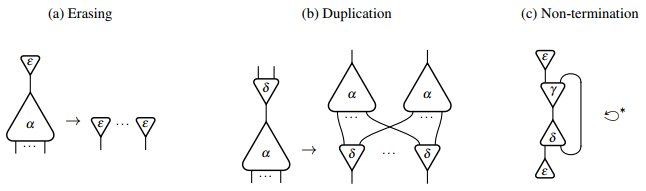
그래픽으로 지우기 및 복제 규칙은 다음과 같이 나타낼 수 있다.

그 자체로 감소하는 비파괴 상호작용 망의 예와 함께.상호작용 미적분학의 해당 구성에서 시작되는 무한 감소 순서는 다음과 같다.

${\displaystyle{\begin{정렬}&, \langle \varnothing)\ \delta(\epsilon ,x)=\gamma(x,\epsilon)\rangle \rightarrow \\&, \langle \varnothing))\epsilon =\gamma(x_{1},x_{2}),\ x=\gamma(y_{1},y_{2}),\ x=\delta(x_{1},y_{1}),\ \epsilon =\delta(x_{2},y_{2})\rangle \rightarrow ^{*}\\&, \langle \varnothing))x_{1}=\epsilon,\ x_{2}=\ep.silon ,\ x=\gamma (y_{1},y_{2}),\ x=\delta (x_{1},y_{1}),\ x_{2}=\epsilon ,\ y_{2}=\epsilon \rangle \rightarrow ^{*}\\&\langle \varnothing \ \ \delta (\epsilon ,x)=\gamma (x,\epsilon )\rangle \rightarrow \dots \end{aligned}}}$

비결정적 확장

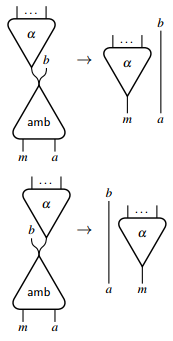
상호작용 그물은 본질적으로 결정론적이며 비결정론적 계산을 직접 모델링할 수 없다.비결정론적 선택을 표현하기 위해서는 상호작용 그물망을 확장할 필요가 있다.실제로 두 개의 주 포트와 다음과 같은 상호 작용 규칙을 가진 ${\text{amb}}$ ^[6] 에이전트 $({\$ 하나만 도입해도 충분하다.

이 고유 에이전트는 모호한 선택을 나타내며 임의 수의 주 포트에서 다른 에이전트를 시뮬레이션하는 데 사용할 수 있다.예를 들어, 다른 인수에 수행되는 계산과는 별개로, 인수가 하나라도 참일 경우 true를 반환하는 ${\text{ParallelOr}}$ ${\$ 부울 ${\text{ParallelOr}}$ 연산을 정의할 수 있다.

참고 항목

참조

^ Lafont, Yves (1990). "Interaction nets". Proceedings of the 17th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages. ACM: 95–108. doi:10.1145/96709.96718. ISBN 0897913434.
^ Mackie, Ian (2008). "An Interaction Net Implementation of Closed Reduction". Implementation and Application of Functional Languages: 20th International Symposium. Lecture Notes in Computer Science. 5836: 43–59. doi:10.1007/978-3-642-24452-0_3. ISBN 978-3-642-24451-3.
^ van Oostrom, Vincent; van de Looij, Kees-Jan; Zwitserlood, Marijn (2010). "Lambdascope: Another optimal implementation of the lambda-calculus" (PDF). Archived from the original (PDF) on 2017-07-06. {{cite journal}}:Cite 저널은 필요로 한다. journal=(도움말)
^ Fernández, Maribel; Mackie, Ian (1999). "A calculus for interaction nets". Principles and Practice of Declarative Programming. Lecture Notes in Computer Science. Springer. 1702: 170–187. doi:10.1007/10704567. ISBN 978-3-540-66540-3.
^ Lafont, Yves (1997). "Interaction Combinators". Information and Computation. Academic Press, Inc. 137 (1): 69–101. doi:10.1006/inco.1997.2643.
^ Fernández, Maribel; Khalil, Lionel (2003). "Interaction Nets with McCarthy's Amb: Properties and Applications". Nordic Journal of Computing. 10 (2): 134–162.

추가 읽기

Asperti, Andrea; Guerrini, Stefano (1998). The Optimal Implementation of Functional Programming Languages. Cambridge Tracts in Theoretical Computer Science. Vol. 45. Cambridge University Press. ISBN 9780521621120.
Fernández, Maribel (2009). "Interaction-Based Models of Computation". Models of Computation: An Introduction to Computability Theory. Springer Science & Business Media. pp. 107–130. ISBN 9781848824348.

외부 링크

de Falco, Marc. "tikz-inet. A set of tikz-based macros for drawing interaction nets".
de Falco, Marc. "INL. Interaction Nets Laboratory".
Vilaça, Miguel. "INblobs. An editor and interpreter for Interaction Nets".
Asperti, Andrea. "The Bologna Optimal Higher-Order Machine".
Salikhmetov, Anton. "JavaScript Engine for Interaction Nets".
Salikhmetov, Anton. "Macro Lambda Calculus".

[1] Lafont, Yves (1990). "Interaction nets". Proceedings of the 17th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages. ACM: 95–108. doi:10.1145/96709.96718. ISBN 0897913434.

[2] Mackie, Ian (2008). "An Interaction Net Implementation of Closed Reduction". Implementation and Application of Functional Languages: 20th International Symposium. Lecture Notes in Computer Science. 5836: 43–59. doi:10.1007/978-3-642-24452-0_3. ISBN 978-3-642-24451-3.

[3] van Oostrom, Vincent; van de Looij, Kees-Jan; Zwitserlood, Marijn (2010). "Lambdascope: Another optimal implementation of the lambda-calculus" (PDF). Archived from the original (PDF) on 2017-07-06. {{cite journal}}:Cite 저널은 필요로 한다. journal=(도움말)

[4] Fernández, Maribel; Mackie, Ian (1999). "A calculus for interaction nets". Principles and Practice of Declarative Programming. Lecture Notes in Computer Science. Springer. 1702: 170–187. doi:10.1007/10704567. ISBN 978-3-540-66540-3.

[5] Lafont, Yves (1997). "Interaction Combinators". Information and Computation. Academic Press, Inc. 137 (1): 69–101. doi:10.1006/inco.1997.2643.

[6] Fernández, Maribel; Khalil, Lionel (2003). "Interaction Nets with McCarthy's Amb: Properties and Applications". Nordic Journal of Computing. 10 (2): 134–162.

[1]

[2]

[3]

[4]

[5]

[6]

Search