역 거리 가중치

역 거리 가중치(IDW)는 알려진 산란 점 집합의 다변량 보간법을 위한 결정론적 방법의 일종이다. 알 수 없는 점에 할당된 값은 알려진 지점에서 사용할 수 있는 값의 가중 평균으로 계산된다.

가중치를 할당할 때 알려진 각 점까지의 거리("근거리 양")의 역에 의존하기 때문에 이러한 유형의 방법에 주어진 이름은 가중 평균에 의해 동기가 부여되었다.

문제의 정의

예상되는 결과는 스터디 영역에서 $u$ 알 수 없는 함수 $u$ $u$ 을(를) 별개로 할당하는 것이다.

u(x):x\to \mathb {R},\quad x\in {D} \subset \mathb {R} ^{n},

여기서 $\mathbf {D}$ ${\$ 는) 스터디 영역이다 $\mathbf {D}$ .

$N$ N $N$ 데이터 지점 집합을 튜플 목록으로 설명할 수 있다.

[(x_{1},u_{1}),(x_{2},u_{2}), ...,(x_{N},u_{N})]

기능은 「매끄러움」(연속적이고 한때는 다른 것)이며, 정확한 (u ( $u(x_{i})=u_{i}$ x $u(x_{i})=u_{i}$ ) $u(x_{i})=u_{i}$ = $u(x_{i})=u_{i}$ $u(x_{i})=u_{i}$ ${\$ 이며, 조사 중인 현상에 대한 사용자의 직관적인 기대에 부응하는 것이다 $u(x_{i})=u_{i}$ 더욱이, 그 기능은 합리적인 비용으로 컴퓨터 어플리케이션에 적합해야 한다(요즘에는 기본적인 구현이 아마도 병렬 자원을 사용할 것이다).

셰퍼드법

과거참조

1965년에 시작된 하버드 컴퓨터 그래픽 및 공간 분석 연구소에서는 다양한 과학자 집단이 모여 현재 지리 정보 시스템이라고 불리는 것을 다시 생각해 보았다.^[1]

실험실의 원동력인 하워드 피셔는 그가 SYMAP라고 부르는 개선된 컴퓨터 지도 프로그램을 구상했다. 처음부터 피셔는 보간법을 개선하기를 원했다. 그는 하버드 대학 신입생들에게 SYMAP에 대한 자신의 연구를 보여주었고, 그들 중 많은 학생들이 실험실 행사에 참여했다. 한 신입생인 도널드 셰퍼드 씨는 SYMAP에서 보간작업을 전면 개편하기로 결정했고, 그 결과 1968년부터 그의 유명한 기사가 나왔다.^[2]

셰퍼드의 알고리즘은 공간 분석으로 작업한 윌리엄 워츠 등 연구소의 이론적 접근법에도 영향을 받았다. 그는 거리의 지수를 가지고 여러 가지 실험을 실시하여 중력 모델에 더 가까운 것(-2의 엑스포트)을 결정했다. 셰퍼드는 기본적인 역 거리 가중치뿐만 아니라 장벽(허용 가능 및 절대적)을 보간으로 허용했다.

다른 연구 센터들은 이 시기에 보간 작업을 하고 있었는데, 특히 캔자스 대학과 그들의 Surface II 프로그램이었다. 그래도 SYMAP의 특징은 학부생이 프로그래밍을 했음에도 불구하고 최첨단의 것이었다.

기본형식

표면

z=\exp(-x^{2}-y^{2})

=

z=\exp(-x^{2}-y^{2})

z=\exp(-x^{2}-y^{2})

(

z=\exp(-x^{2}-y^{2})

-

z=\exp(-x^{2}-y^{2})

2

z=\exp(-x^{2}-y^{2})

-

z=\exp(-x^{2}-y^{2})

z=\exp(-x^{2}-y^{2})

)의

z=\exp(-x^{2}-y^{2})

산란 지점에서 다른 전력 파라미터 p에 대한 셰퍼드 보간법(\

displaystyle z=\exp

=\exp

(-x^{2}-y^{

2}){

2}}}

$i=1,2,...,N$ = $i=1,2,...,N$ , $i=1,2,...,N$ , $i=1,2,...,N$ . $i=1,2,...,N$ . . $i=1,2,...,N$ , N $i=1,2,...,N$ {\ $displaystyle$ i $=$ $1$ , 2, ... $i=1,2,...,N$ 에 $u_{i}=u(x_{i})$ 대해 샘플 $u$ = $u_{i}=u(x_{i})$ u = $u_{i}=u(x_{i})$ $u_{i}=u(x_{i})$ = $u_{i}=u(x_{i})$ $u$ = 1, 2, $..., }$ 을(를 $)$ 기반으로 $x$ 지정된 $i=1,2,...,N$ $지점$ x ${\$ $displaystyle$ $x}$ 에서 $u$ 보간 값 $u$ ${\displaystystyle u}$ 을 찾는 일반적인 형태는 보간 함수:

u(\mathbf {x} )={\begin{cases}{\dfrac {\sum _{i=1}^{N}{w_{i}(\mathbf {x} )u_{i}}}{\sum _{i=1}^{N}{w_{i}(\mathbf {x} )}}},&{\text{if }}d(\mathbf {x} ,\mathbf {x} _{i})\neq 0{\text{ for all }}i,\\u_{i},&{\text{if }}d(\mathbf {x} ,\mathbf {x} _{i})=0{\text{ for some }}i,\end{cases}}

어디에

{\displaystyle w_{i}(\mathbf {x} )={\frac {1}{1}{d(\mathbf {x},\mathbf {x} _{i}^{p}}}}}}}}}}}}}}}}}.

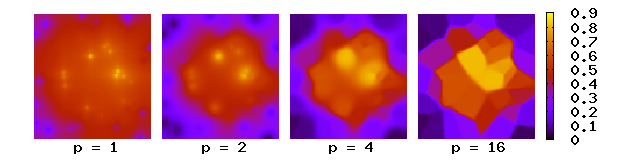
있나 단순한 IDW의 가중치 함수로 Shepard,[2]에 의해 정의된 카메라를 개재(임의의)점, 자이는 보간( 알려진)점, 알려진 점 자이 알 수 없는 점 x에 알려진 포인트 보간과p{p\displaystyle}에서 사용되는, N은 총 횟수보다 d{\displaystyle d}지정된 거리(미터 법의 연산자)를 의미한다. 는 power parameter라고 불리는 양의 실수.

여기서 중량은 보간점에서 거리가 증가함에 따라 감소한다. $p$ $p$ 의 값이 클수록 보간점에 가장 가까운 값에 더 큰 영향을 미치며 $p$ , 그 결과는 큰 p 값에 대해 거의 일정한 보간 값을 갖는 타일의 모자이크(보로노이 다이어그램)로 변한다. 2차원의 경우, 전력 매개변수 $p\leq 2$ $p\leq 2$ $p\leq 2$ $p\leq 2$ 은(는) 데이터 포인트의 $\rho$ 밀도 $\rho$ $\rho$ 과(는) $r_{0}$ 0 ${\displaystyle r_$ ${0$ $}$ $R$ 의 $r_{0}$ 거리 사이의 인접 포인트로 인해 보간된 값이 멀리 떨어져서 지배하게 된다 $p\leq 2$ $R$ 먹음직스럽게

\sum \sum _{j}w_{j}\cHB{0}^{R}{r^{p}}{r^}}=2\pi \rho \int_{r_{0}^{R}^{1-p}\,dr,

$R\rightarrow \infty$ → $【\displaystyle R\rightarrow \inforty$ }과 $R\rightarrow\infty$ p $【\displaystyle$ p $\leq$ 2 $】$ 에 대한 차이 $p\leq 2$ M 치수의 경우, $p\leq M$ $p\leq M$ $p\leq M$ 에 대한 동일한 주장이 있다 $p\leq M$ p 값을 선택하기 위해 보간에서 원하는 평활 정도, 정수 밀도와 분포 등을 고려할 수 있다.rpolated, 그리고 개별 샘플이 주변 샘플에 영향을 미칠 수 있는 최대 거리.

Shepard의 방법은 다음과 같이 정의된 보간점 {x, u}과(와) 보간점_i {x, u_i}의 i tupple 사이의 편차 측정과 관련된 기능을 최소화한 결과다.

\phi(\mathbf {x},u)=\좌측(\sum _{i=0}^{N}{\frac {(u-u_{i})^{d}{d},\mathbf {x}, {i}^{p}}}}}}^{frac {1},}}

최소 조건으로부터 파생된:

{\frac {\phi(\mathbf {x},u)}{\mathbf u}=0.

이 방법은 다른 차원 공간으로 쉽게 확장될 수 있으며 사실상 다차원 공간으로 라그랑주 근사치를 일반화한 것이다. 3변량 보간용으로 설계된 알고리즘의 변형 버전은 Robert J. Renka에 의해 개발되었으며 Toms 라이브러리에서 알고리즘 661로 Netlib에서 이용할 수 있다.

1차원 예제

4개의 산란 지점에서 1차원 보간법으로 p = 2 사용

우카지크-카르모스키 미터법

그러나 세파르트의 방법의 또 다른 수정이 우카지크에 의해 또한 실험 역학에 적용되도록 제안되었다. 제안된 가중치 함수는 다음과 같은 형태를 가지고 있었다.

w_{k}(\mathbf {x})={\frac {1}{1}{{**}(\mathbf {x},\mathbf {x} _{k})^{\frac {1}:{1},},

여기서 $D_{**}(\mathbf {x} ,\mathbf {x} _{k})$ $D_{**}(\mathbf {x} ,\mathbf {x} _{k})$ $D_{**}(\mathbf {x} ,\mathbf {x} _{k})$ ( $D_{**}(\mathbf {x} ,\mathbf {x} _{k})$ , $D_{**}(\mathbf {x} ,\mathbf {x} _{k})$ $D_{**}(\mathbf {x} ,\mathbf {x} _{k})$ ) ${\displaystyle D_{**}(\mathbf {x},\mathbf {x} _{k})$ 는 $D_{{**}}({\mathbf {x}},{\mathbf {x}}_{k})$ 보간점 측정에 대한 통계 오류 확률 분포와 관련하여 선택한 Uwkaszyk–Karmowsi 메트릭이다.

수정 셰퍼드 방법

셰퍼드 방법의 또 다른 수정은 (전체 샘플 대신) R-sphere 내에서 가장 가까운 이웃만 사용하여 보간 값을 계산한다. 이 경우 가중치는 약간 수정된다.

{\displaystyle w_{k}(\mathbf {x})(\mathbf {x},\max(0,R-d)(\mathbf {x},\mathbf {x} _{k})}{Rd(\mathbf {x},\mathbf {k}}}}}\rig)^{2}.

빠른 공간 검색 구조(kd-tree 등)와 결합하면 대규모 문제에 적합한 효율적인 N log N 보간법이 된다.

참조

^ Chrisman, Nicholas. "History of the Harvard Laboratory for Computer Graphics: a Poster Exhibit" (PDF).
^ Jump up to: ^a ^b Shepard, Donald (1968). "A two-dimensional interpolation function for irregularly-spaced data". Proceedings of the 1968 ACM National Conference. pp. 517–524. doi:10.1145/800186.810616.
^ Łukaszyk, S. (2004). "A new concept of probability metric and its applications in approximation of scattered data sets". Computational Mechanics. 33 (4): 299–304. doi:10.1007/s00466-003-0532-2.

참고 항목

커널 밀도 추정

[1] Chrisman, Nicholas. "History of the Harvard Laboratory for Computer Graphics: a Poster Exhibit" (PDF).

[shepardArticle-2] Jump up to: ^a ^b Shepard, Donald (1968). "A two-dimensional interpolation function for irregularly-spaced data". Proceedings of the 1968 ACM National Conference. pp. 517–524. doi:10.1145/800186.810616.

[3] Łukaszyk, S. (2004). "A new concept of probability metric and its applications in approximation of scattered data sets". Computational Mechanics. 33 (4): 299–304. doi:10.1007/s00466-003-0532-2.

[1]

[2]

Search