클라인 그래프
Klein graphs그래프 이론의 수학적 분야에서 클라인 그래프는 서로 다르지만 관련된 두 개의 정규 그래프로서 각각 84개의 가장자리를 가지고 있다.각각은 속 3의 방향성 표면에 내장되어 이중 그래프를 형성할 수 있다.
큐빅 클라인 그래프
| (쿠빅) | |
|---|---|
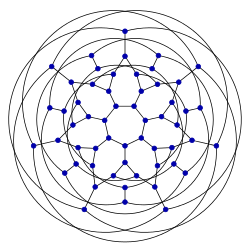 56Klein 그래프 | |
| 이름을 따서 명명됨 | 펠릭스 클라인 |
| 정점 | 56 |
| 가장자리 | 84 |
| 반지름 | 6 |
| 지름 | 6 |
| 둘레 | 7 |
| 자동형성 | 336 |
| 색수 | 3 |
| 색도 지수 | 3 |
| 책두께 | 3 |
| 대기열 번호 | 2 |
| 특성. | 대칭 큐빅 해밀턴어 케이리 그래프 |
| 그래프 및 모수 표 | |
이 그래프는 펠릭스 클라인의 이름을 딴 56개의 정점과 84개의 가장자리를 가진 3개의 정규 그래프다.
해밀턴 그래프다.색도 번호 3, 색도 지수 3, 반지름 6, 직경 6, 둘레 7을 가지고 있다.또한 3-Vertex 연결 그래프와 3-엣지 연결 그래프이기도 하다.책 두께 3과 줄 2가 있다.[1]
속3 오리엔테이블 표면(클라인 쿼틱으로 표현될 수 있음)에 내장할 수 있으며, 여기서 24개의 헵플리 기호 {7,3}8를 가진 "클레인 맵"을 형성한다.
포스터 인구조사에 따르면 F056B로 참조되는 클라인 그래프는 56개의 정점에 있는 유일한 입방 대칭 그래프로서 양립하지 않는다.[2]
28Vex Coxeter 그래프에서 파생될 수 있다.[3]
대수적 특성
클라인 그래프의 자동형 그룹은 순서 336의 그룹 PGL2(7)으로, PSL2(7)을 정상 서브그룹으로 한다.이 그룹은 반쪽 에지에 대해 트랜스적으로 작용하므로 클라인 그래프는 대칭 그래프다.
이 56-vertex 클라인 그래프의 특성 다항식은 x ( )( + 2) ( x - 2) ( + ) ( 2 - 2- ) ( - 2 -1 ) 8 x (x+ ()\)과 같다
갤러리
입체 클라인 그래프의 대체 도면이며, 색도 지수 3이 있는 해밀턴식임을 보여준다.
7-값 클라인 그래프
| (7-값) 클라인 그래프 | |
|---|---|
 24-Klein 그래프 | |
| 이름을 따서 명명됨 | 펠릭스 클라인 |
| 정점 | 24 |
| 가장자리 | 84 |
| 반지름 | 3 |
| 지름 | 3 |
| 둘레 | 3 |
| 자동형성 | 336 |
| 색수 | 4 |
| 색도 지수 | 7 |
| 특성. | 대칭 해밀턴어 |
| 그래프 및 모수 표 | |
이 그래프는 펠릭스 클라인의 이름을 딴 24개의 정점과 84개의 가장자리를 가진 7개의 정규 그래프다.
해밀턴 그래프다.색도 4번, 색도 지수 7번, 반지름 3, 직경 3번, 둘레 3번을 가지고 있다.
그것은 56개의 삼각형 면, 슐레플리 기호 {3,7}8[4]를 가진 "클레인 지도"의 이중을 이루는 속-3 오리엔테이블 표면에 내장될 수 있다.
교차로 배열{ ,4,,1, ,2,} 이([5]가) 있는 고유한 거리 정규 그래프지만 거리 변환 그래프는 아니다
대수적 특성
7-값 클라인 그래프의 자동형 집단은 큐빅 클라인 맵과 같은 순서 336의 그룹이며, 마찬가지로 반쪽 에지에서도 트랜시브하게 작용한다.
이 24-버전스 클라인 그래프의 특성 다항식은( - )( x+ ) ( - ) 과 같다[6]
참조
- ^ Wolz, Jessica; SAT를 이용한 엔지니어링 선형 레이아웃.2018년 튀빙겐 대학교 석사 논문
- ^ Conder, M.; Dobcsányi, P. (2002), "Trivalent symmetric graphs up to 768 vertices", J. Combin. Math. Combin. Comput., 40: 41–63.
- ^ Dejter, Italo. "From the Coxeter graph to the Klein graph". CiteSeer. CiteSeerX 10.1.1.188.2580.
{{cite journal}}:Cite 저널은 필요로 한다.journal=(도움말) - ^ Schulte, Egon; Wills, J. M. (1985). "A Polyhedral Realization of Felix Klein's Map {3, 7}8 on a Riemann Surface of Genus 3". J. London Math. Soc. s2-32 (3): 539–547. doi:10.1112/jlms/s2-32.3.539.
- ^ Brouwer, Andries; Cohen, Arjeh; Neumaier, Arnold (1989). Distance-Regular Graphs. Springer-Verlag. p. 386. ISBN 978-0-387-50619-7.
- ^ van Dam, E. R.; Haemers, W. H.; Koolen, J. H.; Spence, E. (2006). "Characterizing distance-regularity of graphs by the spectrum". J. Combin. Theory Ser. A. 113 (8): 1805–1820. doi:10.1016/j.jcta.2006.03.008.





