왜곡(광학)

v; t; 광학적 수차
	디포커스; 기울이다; 구면 수차; 난시; 혼수상태 ; 왜곡.; 페츠발장 곡률; 색수차

기하학 광학에서 왜곡은 직선 투영으로부터의 편차입니다. 즉, 장면의 직선이 이미지에서 직선으로 유지되는 투영입니다.그것은 광학적 수차의 한 형태이다.

반지름 왜곡

배럴

핀쿠션

콧수염

반지름 왜곡의 예

왜곡은 불규칙하거나 많은 패턴을 따를 수 있지만, 가장 일반적으로 발생하는 왜곡은 방사 대칭이거나 사진 렌즈의 대칭에서 발생하는 대략적인 왜곡입니다.이러한 반경 왜곡은 보통 배럴 왜곡 또는 핀추션 ^[1]왜곡으로 분류할 수 있습니다.

Barrel distortion: 배럴 왜곡에서는 광축으로부터의 거리에 따라 이미지 배율이 감소합니다.분명한 효과는 구체(또는 배럴)를 중심으로 매핑된 이미지의 효과입니다.어안렌즈는 반구면을 촬영하여 무한히 넓은 물체 평면을 유한한 이미지 영역으로 매핑하는 방법으로 이러한 왜곡 유형을 활용한다.줌 렌즈에서는, 렌즈의 초점 거리 범위의 중앙에서 배럴 왜곡이 나타나고,^[2] 범위의 광각 끝에서는 최악입니다.오목한(마이너스) 구면 렌즈는 배럴 왜곡이 발생하는 경향이 있습니다.
Pincushion distortion: 핀쿠션 왜곡에서는 광축으로부터의 거리에 따라 화상 배율이 증가합니다.가시적인 효과는 이미지 중심을 통과하지 않은 선이 핀추션처럼 이미지 중심을 향해 안쪽으로 휘어지는 것입니다.볼록(+) 구면 렌즈는 핀쿠션 왜곡이 있는 경향이 있습니다.
Mustache distortion: 콧수염 변형(수염 변형) 또는 복합 변형이라고도 하는 두 유형의 혼합물은 흔하지는 않지만 드물지는 않습니다.이미지 중심 부근에서 배럴 왜곡으로 시작해 이미지 주변으로 향하는 핀추션 왜곡으로 서서히 바뀌어 프레임 상부의 수평선이 핸들 바 수염처럼 보입니다.

수학적으로, 배럴과 핀쿠션 왜곡은 2차이며, 이는 중심으로부터의 거리 제곱에 따라 증가함을 의미합니다.콧수염 왜곡에서는 4차항(도 4)이 유의합니다.중앙에서는 2도 배럴 왜곡이 우세하지만, 가장자리에서는 핀쿠션 방향의 4도 왜곡이 우세합니다.다른 왜곡은 원칙적으로 가능한데, 가장자리에 있는 중앙과 배럴의 핀추션 또는 고차 왜곡(도 6, 8)이 있지만 일반적으로 실용적인 렌즈에서는 발생하지 않으며 고차 왜곡은 메인 배럴 및 핀추션 효과에 비해 작습니다.

발생.

단순한 팬(왼쪽)과 비교한 지구본 효과(오른쪽)의 시뮬레이션 애니메이션

사진술에서 왜곡은 특히 줌 렌즈, 특히 장거리 줌과 관련이 있지만, 초점 거리에 따라 다를 수 있습니다. 예를 들어 Canon EF 50mm f/1.4는 초점 거리가 매우 짧을 때 배럴 왜곡을 나타냅니다.배럴 왜곡은 광각 렌즈에서 볼 수 있으며 줌 렌즈의 광각 끝에서 자주 볼 수 있는 반면 핀쿠션 왜곡은 구형 또는 로우엔드 망원 렌즈에서 자주 볼 수 있습니다.콧수염 왜곡은 특정 역초점 렌즈를 사용하는 줌의 넓은 끝에서 특히 관찰되며, 최근에는 니콘 18–200 mm와 같은 대형 줌에서 관찰된다.

쌍안경 같은 시각 광학 기기로 특정 양의 핀쿠션 왜곡이 종종 발견되며, 지구 효과를 제거하는 역할을 한다.

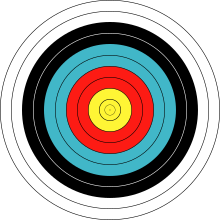
방사형 왜곡은 양궁 표적과 같이 동심원에 미치는 영향을 통해 이해할 수 있습니다.

이러한 왜곡을 이해하기 위해서는 이것들은 방사상의 결함이라는 것을 기억해야 한다.문제의 광학 시스템은 회전대칭(비방사상의 결함 제외)을 가지고 있기 때문에 실제로 올바른 테스트 이미지는 사격수의 표적과 같은 균일한 분리를 가진 동심원 세트이다.그런 다음 이러한 일반적인 왜곡이 실제로 개체에서 이미지로의 비선형 반지름 매핑을 의미함을 관찰할 수 있습니다.핀쿠션 왜곡은 실제로는 작은 반지름에 비해 큰 반지름에 대한 과장된 반지름 매핑일 뿐입니다.(객체에서 영상으로) 반지름 변환을 보여주는 그래프는 상단(맨 오른쪽)에서 더 가파릅니다.반대로 배럴 왜곡은 실제로 작은 반지름에 비해 큰 반지름에 대한 축소 반지름 매핑입니다.객체에서 이미지로의 반지름 변환을 보여주는 그래프는 상단(오른쪽 끝)에서 덜 가파릅니다.

색수차

파장에 따라 달라지는 반지름 왜곡을 "가로 색 수차" – "가로 색수차"라고 합니다. 왜냐하면 방사형이기 때문입니다. 색(파장)에 따라 달라지기 때문입니다.이로 인해 이미지 바깥쪽의 고대비 영역에 색상의 테두리가 생길 수 있습니다.이것은 축(종방향) 색수차와 혼동해서는 안 되며, 이는 필드 전체에 걸쳐 이상, 특히 보라색 프링의 원인이 된다.

용어의 출처

이러한 왜곡의 이름은 시각적으로 유사한 익숙한 물체에서 유래했습니다.

배럴 왜곡에서 직선은 배럴에서와 같이 중심에서 바깥쪽으로 돌출됩니다.
핀쿠션 왜곡에서는 사각형의 모서리가 쿠션처럼 가늘고 긴 점을 형성합니다.
콧수염 변형에서는 수평선이 중앙에서 위로 튀어나온 다음 프레임의 가장자리(프레임 상단에 있는 경우)에 접근할 때 반대 방향으로 구부러집니다(컬 핸들 바의 경우).

소프트웨어 수정

보정되지 않은 배럴 왜곡 포함(26mm)

소프트웨어로 배럴 왜곡 보정(이것이 ENIAC 컴퓨터)

주로 저차 방사형 구성요소에 ^[3]의해 지배되는 방사형 왜곡은 Conrady의 ^[5]초기 연구에 기초한 Brown-Conrady 모델이라고도 하는 Brown의 왜곡 ^[4]모델을 사용하여 보정할 수 있습니다.브라운-콘레이디 모델은 렌즈의 물리적 요소가 완벽하게 정렬되지 않아 발생하는 반지름 왜곡과 접선 왜곡을 모두 보정합니다.후자는 변위 왜곡이라고도 합니다.반지름 왜곡에 대한 자세한 내용은 Zhang을 참조하십시오^[6].브라운 콘레이디 왜곡 모델은

{\displaystyle{\begin{alignedat}{3}x_{\mathrm{마}}=x_{\mathrm{d}}&+(x_{\mathrm{d}}-x_{\mathrm{c}})(K_{1}r^{2}+K_{2}r^{4}+\cdots)+(P_{1}(r^{2}+2(x_{\mathrm{d}}-x_{\mathrm{c}})^{2})\\&, +2.P_ᆫ(x_{\mathrm{d}}-x_{\mathrm{c}})(y_{\mathrm{d}}-y_{\mathrm{c}}))(1+P_{3}r^{2}+P_{4}r^{4}\cdots)\\y_{\mathrm{마}}=y_{\mathrm{d}}&+(y_{\mat.hrm {d}-y_{\mathrm {c}}(K_{1}r^{2}+K_{2}r^{4}+\cdots)+(2P_{1}(x_{\mathrm {c}})-x_{\mathrm {c}-{d})-y})

어디에

$(x_{\mathrm {d} },\ y_{\mathrm {d} })$ $(x_{\mathrm {d} },\ y_{\mathrm {d} })$ , $(x_{\mathrm {d} },\ y_{\mathrm {d} })$ d ) $(x_{\mathrm {d} },\ y_{\mathrm {d} })$ { $displaystyle$ ( x $_$ { \ $mathrm$ { $d }$ , \ y _ { \ $mathrm$ { $d }$ } )는 $(x_{\mathrm {d} },\ y_{\mathrm {d} })$ 지정된 렌즈를 사용하여 이미지 평면에 투영된 왜곡된 이미지 포인트입니다.
$(x_{\mathrm {u} },\ y_{\mathrm {u} })$ $(x_{\mathrm {u} },\ y_{\mathrm {u} })$ u , $(x_{\mathrm {u} },\ y_{\mathrm {u} })$ u $(x_{\mathrm {u} },\ y_{\mathrm {u} })$ ) { $displaystyle$ ( x $_$ { \ $mathrm { u$ } , \ y _ { \ $mathrm { u }$ )는 $(x_{\mathrm {u} },\ y_{\mathrm {u} })$ 이상적인 핀홀카메라에 의해 투영되는 왜곡되지 않은 이미지 포인트입니다.
$(x_{\mathrm {c} },\ y_{\mathrm {c} })$ $(x_{\mathrm {c} },\ y_{\mathrm {c} })$ c , $(x_{\mathrm {c} },\ y_{\mathrm {c} })$ ) { $displaystyle$ ( x $_$ { \ $mathrm$ { $c }$ , \ y $_$ { \ $mathrm$ { $c }$ } )는 $(x_{\mathrm {c} },\ y_{\mathrm {c} })$ 왜곡 중심입니다.
$(\$ 은 $K_{n}$ $n^{\mathrm {th} }$ $(\$ n $^{\mathrm {th}})$ 방사 $n^{\mathrm {th} }$ $n^{\mathrm {th} }$ 계수입니다.
$(\$ 은 $P_{n}$ $n^{\mathrm {th} }$ $(\$ n $^{\mathrm {th}})$ 접선 $n^{\mathrm {th} }$ 왜곡 계수입니다.
$r$ {\ $displaystyle$ r $}$ ${\sqrt {(x_{\mathrm {d} }-x_{\mathrm {c} })^{2}+(y_{\mathrm {d} }-y_{\mathrm {c} })^{2}}}$ ( ${\sqrt {(x_{\mathrm {d} }-x_{\mathrm {c} })^{2}+(y_{\mathrm {d} }-y_{\mathrm {c} })^{2}}}$ x ${\sqrt {(x_{\mathrm {d} }-x_{\mathrm {c} })^{2}+(y_{\mathrm {d} }-y_{\mathrm {c} })^{2}}}$ - ${\sqrt {(x_{\mathrm {d} }-x_{\mathrm {c} })^{2}+(y_{\mathrm {d} }-y_{\mathrm {c} })^{2}}}$ ${\sqrt {(x_{\mathrm {d} }-x_{\mathrm {c} })^{2}+(y_{\mathrm {d} }-y_{\mathrm {c} })^{2}}}$ ) ${\sqrt {(x_{\mathrm {d} }-x_{\mathrm {c} })^{2}+(y_{\mathrm {d} }-y_{\mathrm {c} })^{2}}}$ 2 + ${\sqrt {(x_{\mathrm {d} }-x_{\mathrm {c} })^{2}+(y_{\mathrm {d} }-y_{\mathrm {c} })^{2}}}$ ( ${\sqrt {(x_{\mathrm {d} }-x_{\mathrm {c} })^{2}+(y_{\mathrm {d} }-y_{\mathrm {c} })^{2}}}$ d ${\sqrt {(x_{\mathrm {d} }-x_{\mathrm {c} })^{2}+(y_{\mathrm {d} }-y_{\mathrm {c} })^{2}}}$ - ${\sqrt {(x_{\mathrm {d} }-x_{\mathrm {c} })^{2}+(y_{\mathrm {d} }-y_{\mathrm {c} })^{2}}}$ ${\sqrt {(x_{\mathrm {d} }-x_{\mathrm {c} })^{2}+(y_{\mathrm {d} }-y_{\mathrm {c} })^{2}}}$ ) ${\sqrt {(x_{\mathrm {d} }-x_{\mathrm {c} })^{2}+(y_{\mathrm {d} }-y_{\mathrm {c} })^{2}}}$ 2 { $displaystyle { x$ _ { \ $mathrm$ { d } - $x$ _ { \ $mathrm { c$ } } )^{2 $}$ + ( y $_$ { \ $mathrm { c$ } $)$ } - y _ { { c } ${\sqrt {(x_{\mathrm {d} }-x_{\mathrm {c} })^{2}+(y_{\mathrm {d} }-y_{\mathrm {c} })^{2}}}$ } 、、、、 image image image image image image image image image image image image image and and and image and and and 。

배럴 왜곡은 일반적으로 K $(\$ 에 $K_{1}$ $K_{1}$ 음의 용어를 사용하는 반면 핀쿠션 왜곡은 양의 값을 가집니다.콧수염 왜곡에는 비단조 방사형 기하학 계열이 있으며, $일부$ r\ $displaystyle$ r의 $r$ 경우 시퀀스가 부호를 변경합니다.

반지름 왜곡을 모델링하기 위해 분할^[7] 모델은 일반적으로 브라운-콘라디의 짝수 차수 다항식 ^[8]모델보다 더 정확한 근사치를 제공한다.

{\mathrm {u} x_{\mathrm {c} + {\frac {x_{\mathrm {d} } - x_{\mathrm {c} } {1+K_{1}r^{2} + K_{2}^4+cdots\cdots} }

이전에 정의한 것과 동일한 파라미터를 사용합니다.반지름 왜곡의 경우 심각한 ^[8]왜곡을 보다 정확하게 설명하는 데 필요한 용어가 적기 때문에 이 분할 모델이 브라운-콘레이디 모델보다 선호된다.이 모델을 사용하면 보통 단일 항으로 대부분의 ^[9]카메라를 모델링할 수 있습니다.

소프트웨어는 이미지를 반대로 왜곡함으로써 이러한 왜곡을 수정할 수 있습니다.여기에는 왜곡방정식의 ^[3]비선형성으로 인해 중요하지 않은 각 왜곡된 픽셀에 대응하는 왜곡된 픽셀의 판별이 포함됩니다.적색, 녹색 및 청색에 대해 별도로 이러한 왜곡을 적용함으로써 측색 수차(보라색/녹색 주름)를 크게 줄일 수 있다.

왜곡 또는 왜곡 해제에는 일반적으로 분석 솔루션이 부족한 비선형 문제를 반전하거나 계수를 둘 다 사용해야 합니다.근사, 국소 선형화 및 반복 솔버와 같은 표준 접근법이 모두 적용됩니다.어떤 솔버가 바람직한지는 필요한 정확도와 사용 가능한 계산 리소스에 따라 달라집니다.

교정 완료

보정된 시스템은 렌즈/카메라 전송 기능 표에서 작동합니다.

Adobe Photoshop Lightroom 및 Photoshop CS5는 복잡한 왜곡을 수정할 수 있습니다.
PTlens는 복잡한 왜곡을 수정하는 Photoshop 플러그인 또는 독립 실행형 애플리케이션입니다.선형 왜곡뿐만 아니라 2도 이상의 비선형 구성 ^[10]요소도 보정합니다.
Lensfun은 렌즈 ^[11]^[12]왜곡을 보정하기 위해 데이터베이스와 라이브러리를 무료로 사용할 수 있습니다.
OpenCV는 컴퓨터 비전(멀티 언어, 멀티 OS)용 오픈 소스 BSD 라이센스 라이브러리입니다.카메라 ^[13]보정 모듈을 갖추고 있습니다.
DxO의 PhotoLab 소프트웨어는 복잡한 왜곡을 보정할 수 있으며 초점 거리를 고려합니다.
proDAD Defishr에는 Unwarp 툴과 Calibrationator 툴이 포함되어 있습니다.체커보드 패턴의 왜곡에 의해 필요한 언랩을 산출한다.
Micro Four Third 시스템 카메라 및 렌즈는 각 렌즈의 펌웨어에 저장된 보정 파라미터를 사용하여 자동 왜곡 보정을 수행하며 카메라 및 원시 컨버터 소프트웨어에 의해 자동으로 적용됩니다.이러한 렌즈의 대부분은, 이러한 자동 보정을 실시하지 않는 시스템에서는, 다른 렌즈에 비해 왜곡이 큰 것을 특징으로 하고 있습니다만, 소프트웨어에 의해서 보정된 최종 화상은,^[14] 경쟁하는 설계보다 왜곡이 현저하게 적은 것을 나타내고 있습니다.

설명서

수동 시스템에서는 왜곡 파라미터를 수동으로 조정할 수 있습니다.

Image Magick은 몇 가지 왜곡을 수정할 수 있습니다.예를 들어 일반적인 GoPro Hero3+ Silver 카메라의 어안 왜곡은 명령어로^[15] 수정할 수 있습니다.

convert distorted_image.jpg -distort barrel "0.06335 -0.18432 -0.13009" corrected_image.jpg

Photoshop CS2 및 Photoshop Elements(버전 5부터)에는 수동 렌즈 보정 필터가 포함되어 있어 간단한 (핀치션/배럴) 왜곡이 가능합니다.
Corel Paint Shop Pro Photo에는 간단한(배럴, 어안, 구면 및 핀쿠션) 왜곡을 위한 수동 렌즈 왜곡 효과가 포함되어 있습니다.
GIMP에는 수동 렌즈 왜곡 보정이 포함되어 있습니다(버전 2.4 이후).
PhotoPerfect는 일반적인 핀쿠션 조정 및 프린지 조정(빨강, 녹색, 파란색 이미지 부분의 크기 조정)을 위한 인터랙티브 기능을 갖추고 있습니다.
Hugin은 왜곡을 수정하는 데 사용할 수 있지만, Hugin의 주요 ^[16]용도는 아닙니다.

이미지를 처리하는 시스템 외에 비디오의 왜곡 파라미터를 조정하는 시스템도 있습니다.

「렌즈 보정」비디오 필터를 사용하는 FFMPEG.^[17]
노드 편집기를 사용하여 입력 노드와 출력 노드 사이에 "Distort/Lens Distribution" 노드를 삽입하여 블렌더합니다.

「」를 참조해 주세요.

레퍼런스

^ Paul van Walree. "Distortion". Photographic optics. Archived from the original on 29 January 2009. Retrieved 2 February 2009.
^ "Tamron 18-270mm f/3.5-6.3 Di II VC PZD". Retrieved 20 March 2013.
^ ^a ^b ^c de Villiers, J. P.; Leuschner, F.W.; Geldenhuys, R. (17–19 November 2008). "Centi-pixel accurate real-time inverse distortion correction" (PDF). 2008 International Symposium on Optomechatronic Technologies. SPIE. doi:10.1117/12.804771.
^ Brown, Duane C. (May 1966). "Decentering distortion of lenses" (PDF). Photogrammetric Engineering. 32 (3): 444–462. Archived from the original (PDF) on 12 March 2018.
^ Conrady, A. E. (1919). "Decentred Lens-Systems". Monthly Notices of the Royal Astronomical Society. 79 (5): 384. Bibcode:1919MNRAS..79..384C. doi:10.1093/mnras/79.5.384.
^ Zhang, Zhengyou (1998). A Flexible New Technique for Camera Calibration (PDF) (Technical report). Microsoft Research. MSR-TR-98-71.
^ Fitzgibbon, A. W. (2001). "Simultaneous linear estimation of multiple view geometry and lens distortion". Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR). IEEE. doi:10.1109/CVPR.2001.990465.
^ ^a ^b Bukhari, F.; Dailey, M. N. (2013). "Automatic Radial Distortion Estimation from a Single Image" (PDF). Journal of mathematical imaging and vision. Springer. doi:10.1007/s10851-012-0342-2.
^ Wang, J.; Shi, F.; Zhang, J.; Liu, Y. (2008). "A new calibration model of camera lens distortion". Pattern Recognition. Elsevier. doi:10.1016/j.patcog.2007.06.012.
^ "PTlens". Retrieved 2 January 2012.
^ "Lensfun". Retrieved 16 April 2022.
^ "lensfun - Rev 246 - /trunk/README". Archived from the original on 13 October 2013. Retrieved 13 October 2013.
^ "OpenCV". opencv.org/. Retrieved 22 January 2018.
^ Wiley, Carlisle. "Articles: Digital Photography Review". Dpreview.com. Archived from the original on 7 July 2012. Retrieved 3 July 2013.
^ "ImageMagick v6 Examples -- Lens Corrections".
^ "Hugin tutorial – Simulating an architectural projection". Retrieved 9 September 2009.
^ "FFmpeg Filters Documentation".

외부 링크

[van_Walree-1] Paul van Walree. "Distortion". Photographic optics. Archived from the original on 29 January 2009. Retrieved 2 February 2009.

[2] "Tamron 18-270mm f/3.5-6.3 Di II VC PZD". Retrieved 20 March 2013.

[devilliers-3] Villiers, J. P.; Leuschner, F.W.; Geldenhuys, R. (17–19 November 2008). "Centi-pixel accurate real-time inverse distortion correction" (PDF). 2008 International Symposium on Optomechatronic Technologies. SPIE. doi:10.1117/12.804771.

[brown-4] Brown, Duane C. (May 1966). "Decentering distortion of lenses" (PDF). Photogrammetric Engineering. 32 (3): 444–462. Archived from the original (PDF) on 12 March 2018.

[5] Conrady, A. E. (1919). "Decentred Lens-Systems". Monthly Notices of the Royal Astronomical Society. 79 (5): 384. Bibcode:1919MNRAS..79..384C. doi:10.1093/mnras/79.5.384.

[zhang-6] Zhang, Zhengyou (1998). A Flexible New Technique for Camera Calibration (PDF) (Technical report). Microsoft Research. MSR-TR-98-71.

[fitzgibbon-7] Fitzgibbon, A. W. (2001). "Simultaneous linear estimation of multiple view geometry and lens distortion". Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR). IEEE. doi:10.1109/CVPR.2001.990465.

[bukhari-8] Bukhari, F.; Dailey, M. N. (2013). "Automatic Radial Distortion Estimation from a Single Image" (PDF). Journal of mathematical imaging and vision. Springer. doi:10.1007/s10851-012-0342-2.

[wang-9] Wang, J.; Shi, F.; Zhang, J.; Liu, Y. (2008). "A new calibration model of camera lens distortion". Pattern Recognition. Elsevier. doi:10.1016/j.patcog.2007.06.012.

[10] "PTlens". Retrieved 2 January 2012.

[11] "Lensfun". Retrieved 16 April 2022.

[12] "lensfun - Rev 246 - /trunk/README". Archived from the original on 13 October 2013. Retrieved 13 October 2013.

[13] "OpenCV". opencv.org/. Retrieved 22 January 2018.

[14] Wiley, Carlisle. "Articles: Digital Photography Review". Dpreview.com. Archived from the original on 7 July 2012. Retrieved 3 July 2013.

[15] "ImageMagick v6 Examples -- Lens Corrections".

[16] "Hugin tutorial – Simulating an architectural projection". Retrieved 9 September 2009.

[17] "FFmpeg Filters Documentation".

[1]

[2]

[3]

[5]

[4]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

Search

왜곡(광학)

네임스페이스

더

목차

반지름 왜곡

발생.

색수차

용어의 출처

소프트웨어 수정

교정 완료

설명서

관련 현상

「」를 참조해 주세요.

레퍼런스

외부 링크

Search

왜곡(광학)

반지름 왜곡

발생.

색수차

용어의 출처

소프트웨어 수정

교정 완료

설명서

관련 현상

「 」를 참조해 주세요.

레퍼런스

외부 링크

「」를 참조해 주세요.