거리 측정
Distance measure| 시리즈의 일부 |
| 물리 우주론 |
|---|
거리 측정은 물리 우주론에서 두 물체 또는 우주의 사건 사이의 거리에 대한 자연스러운 개념을 제공하기 위해 사용됩니다.관측 가능한 양(먼 퀘이사의 광도, 먼 은하의 적색 편이, 우주 마이크로파 배경(CMB) 파워 스펙트럼의 음향 피크의 각도 크기 등)을 직접 관측할 수 없지만 계산에 더 편리한 다른 양에 연결하기 위해 종종 사용됩니다.퀘이사, 은하 등의 방사성 물질)여기서 설명하는 거리 측정치는 모두 낮은 적색 편이에서의 유클리드 거리에 대한 일반적인 개념으로 축소된다.
우주론에 대한 우리의 현재 이해에 따라, 이러한 측정치는 일반 상대성 이론의 맥락에서 계산되며, 여기서 프리드만-레미트레-로버톤-워커 해법은 우주를 묘사하기 위해 사용됩니다.
개요
우주론에는 작은 적색편이를 위해 점근적으로 하나씩 "거리"에 대한 몇 가지 다른 정의가 있습니다.빨간색 시프트는 항상 관측 가능하기 때문에 이러한 거리에 대한 표현은 시프트z {z의 함수로 작성될 때 가장 실용적입니다.스케일 a /( + 의 함수로도 쓸 수 있습니다 {{ a
이 문서의 나머지 부분에서는 달리 명시되지 않는 한 고유 속도는 무시할 수 있는 것으로 가정한다.
먼저 몇 가지 거리 측정에 대한 공식을 제공한 다음, 더 자세히 설명합니다."허블 거리"를 다음과 같이 정의합니다.
서c {\ c는 빛의 속도, 은 현재 Hubble 매개변수, h는 무차원 허블 상수이며 모든 거리는 z H z0})에 대해 점근입니다. 작은 z.
또한 무차원 허블 [1]파라미터도 정의합니다.
여기서 r m {\_{_{ λ \displaystyle \Omega _는 각각 현재의 방사 에너지 밀도, 물질 밀도, "암흑 에너지 밀도"의 정규화 값이다(후자는 우주 상수, 1- _ _{ _}}는 곡률을 결정합니다.된 적색 이동에서 허블 파라미터는 H E { H)=
대부분의 다른 공식의 기초가 되는 결합 거리 공식은 적분을 포함한다.일부 제한된 매개변수 선택(아래 참조)의 경우 결합 거리 적분은 폐쇄 분석 형식을 갖지만, 일반적으로, 특히 우리 우주의 매개변수에 대해서는 수치로만 해결책을 찾을 수 있습니다.우주론자들은 일반적으로 관찰자에서 물체까지의 거리를 LOS([2]시선)를 따라 적색 z(\z)로 측정할 때 다음과 같은 방법을 사용합니다.
- 결합 거리:
- 횡단 결합 거리:
- 각 직경 거리:
- 광도 거리:
- 광이동 거리:
대체 용어
피블스(1993)는 횡방향 공동 거리를 "각도 크기 거리"라고 부르는데, 각 지름 거리로 [1]오인해서는 안 된다. 기호 \chi r r이 결합 및 각 직경의 거리를 나타내기 위해 사용됩니다.때때로 광이동 거리는 "눈길 거리" 및/또는 "눈길 시간"[citation needed]이라고도 합니다.
세부 사항
고유 속도
실제 관측에서는 허블 흐름에 대한 지구의 움직임이 관측된 적색편이에 영향을 미칩니다.
레드시프트에는 사실 두 가지 개념이 있습니다.하나는 우주 마이크로파 배경에 의해 정의되는 "공생" 주변(허블 흐름)에 대해 지구와 물체가 모두 움직이지 않을 때 관측되는 적색 이동입니다.다른 하나는 관측된 물체의 고유 속도와 우리의 고유 속도에 따라 달라지는 실제 적색편이 측정값입니다.태양계는 Leo와 Crater 사이의 방향으로 약 370km/s의 속도로 이동하기 때문에, 그 방향으로 멀리 있는 물체는 1(표시 스타일 1하며, 반대 방향으로 멀리 있는 물체는 약 1.0012배 합니다.(태양 주위를 도는 지구의 운동 속도는 초속 30km에 불과합니다.)
결합 거리
기본 관측자, 즉 허블 흐름과 함께 움직이는 관측자 사이의 결합 C는 결합 거리가 우주의 팽창을 설명하므로 시간에 따라 변하지 않습니다.결합 거리는 시선(LOS)을 따라 가까운 기본 관측자의 적절한 거리를 통합함으로써 얻을 수 있는 반면, 적절한 거리는 일정한 우주 시간에서의 측정치가 산출하는 값이다.
표준 우주론에서, 결합 거리와 적절한 거리는 우주학자들이 물체 사이의 거리를 측정하기 위해 사용하는 밀접하게 연관된 두 개의 거리 측정 단위이다. 결합 거리는 현재 적절한 거리이다.
공역 거리(자신의 움직임을 약간 보정하는 것)는 시차에서 얻을 수 있는 거리입니다. 왜냐하면 시차는 현재 태양을 통과하고 멀리 있는 물체를 중심으로 360°를 곱한 원의 둘레에 대한 천문 단위의 비율과 같기 때문입니다.그러나 메가파섹 이상의 물체는 시차가 너무 작아서 측정할 수 없습니다(Gaia 우주 망원경은 가장 밝은 별의 시차를 7마이크로아크로초의 정밀도로 측정합니다). 따라서 우리 국부 은하군 밖에 있는 은하의 시차는 너무 작아서 측정할 수 없습니다.
δ m { _} = \ _{= 0}인 경우/ )인 경우 스케일 팩터를\ a로 치환하여 공역 거리의 정의에 대한 닫힌 형식이 있습니다.현재 우리 우주는 r k { _}=\ _}= 이 경우 다음과 같이 표시됩니다.
어디에
결합 거리는 물체나 우리가 특이한 속도를 가지지 않는 경우 관련되는 z 값을 사용하여 계산해야 합니다.
스케일 팩터와 함께 적절한 거리를 제공합니다.
적정 거리
적절한 거리는 우주의 팽창으로 인해 시간이 지남에 따라 변할 수 있는 우주론적 시간의 특정 순간에 멀리 있는 물체가 어디에 있는지와 대략 일치합니다.우주의 팽창에 따른 시간적 변화 없는 거리를 제공하는 결합 거리 요인(단 내 은하의 움직임과 같은 다른 국지적 요인에 의해 변경될 수 있음)입니다. 결합 거리는 현재 적절한 거리입니다.
횡방향 결합 거리
하늘에서 각도로 분리된 일정한 적색 편이 의 2개의 공동물체는 거리 ( 를 갖는다고 합니다. 여기서 횡단결합거리(\ display display distance d)는 적절한 값입니다리.y.
각지름 거리
의 xx}, 각도 크기({인 것으로 보이는 개체는 d ( x / {)= \의 각 직경 거리를 가집니다. 이는 일반적으로 눈금자 i를 관측하기 위해 사용됩니다.n 바리온 음향 진동의 맥락.
지구의 고유 속도를 계산할 때는 해당 경우에 해당하는 빨간색 시프트를 사용해야 태양계 운동을 방향에 따라 0.99867~1.00133의 비율로 보정해야 한다.(물체를 향해 속도 v로 이동하기 시작하면, 어느 거리에서든 해당 물체의 각 지름은 ( /)/ ( - /) . {\ { ( + / ) / ( 1 - v / c ) 。{ { ( 1 + c ) / ( 1 - v / c )} } 。)
광도 거리
원거리 물체의 고유 L({L을 알고 있는 플럭스 S({ S})를 측정하여 광도 거리를 계산하고 위의 식과 동일한 L / 4 †({) =L/4 S를 구한다. {{ 이 양은 우주의 팽창 가속도를 발견하기 위해 최초로 사용된 Ia형 초신성과 같은 표준 초의 측정에 중요합니다.
지구의 고유속도를 고려할 때, 이 경우에 해당하는 적색편이를 M, {에 해야 하지만 계수(+) {+는 측정된 적색편이를 사용해야 하며 물체의 고유속도에 을 곱하여 다시 보정해야 한다. /)/ (1 - /), {\ 여기서 v는 우리에게서 떨어진 객체의 고유 속도의 구성요소입니다.이렇게 하면 광도 거리는 Etherington의 상호성 정리(아래 참조)에 따라 (+ ),(\ (에각 직경 거리를 곱한 것과 같습니다. 여기서 z는 측정된 적색 편이입니다.
광이동 거리
이 d {\은 물체에서 관찰자에게 빛이 도달하는 데 걸린 시간과 빛의 속도를 곱한 시간입니다.예를 들어, 이 거리 측정에서 관측 가능한 우주의 반지름은 우주의 나이와 빛의 속도(1광년/년)를 곱한 값이 되며, 이는 약 138억 광년으로 밝혀집니다.
r m { displaystyle \_ {r= \ _ { m } =}이면 광이동 거리의 닫힌 형태 해법(우주론적 삼각함수인 경우 arcoshstyle \ { } } inversisplaystyle _ { m} = 0)이 있다.tant에는 다른 기호가 있습니다). r _{r}=\ _ }=인 경우, z 는 아니지만 d 는 폐쇄형 솔루션이 있습니다
두 거리 측정치가 평평한 우주에서 동일하도록 한계 k _ 0을 취함으로써 교차 결합 거리로부터 결합 거리를 회복한다는 점에 유의하십시오.
그러면 우주의 나이는 z T(z) / \ _ {{t이후 지금까지의 시간은 t ( d / t t(z이다.
Etherington 거리 이중성
Etherington의 거리-이중 방정식은 표준 초의 광도 거리와 각지름 거리 사이의 관계입니다. L ( + ) d {\ }=(12}
「 」를 참조해 주세요.
레퍼런스
- ^ a b Peebles, P. J. E. (1993). Principles of Physical Cosmology. Princeton University Press. pp. 310–320. Bibcode:1993ppc..book.....P. ISBN 978-0-691-01933-8.
- ^ David W. Hogg (2000). "Distance measures in cosmology". arXiv:astro-ph/9905116v4.
- ^ Staff (2022). "Cosmology Calculator". International Centre for Radio Astronomy Research. Retrieved 4 August 2022.
- ^ I.M.H. Etherington, "LX. 일반상대성이론의 거리 정의에 대하여", 철학잡지 제15권, S. 7(1933), 페이지 761-773.
- Scott Dodelson, 현대 우주론입니다.학술용 프레스(2003년).



 빛의
빛의  현재 Hubble 매개변수,
현재 Hubble 매개변수, 


 각각 현재의 방사 에너지 밀도, 물질 밀도, "
각각 현재의 방사 에너지 밀도, 물질 밀도, "






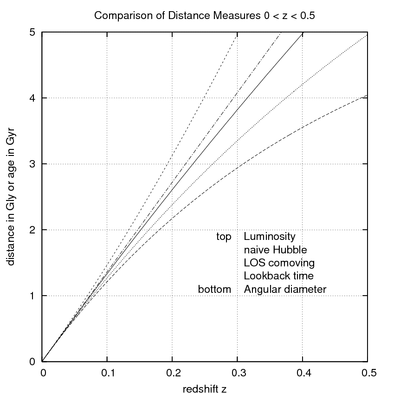


 Omega 파라미터의 합계가 1이 되도록 선택됩니다.
Omega 파라미터의 합계가 1이 되도록 선택됩니다.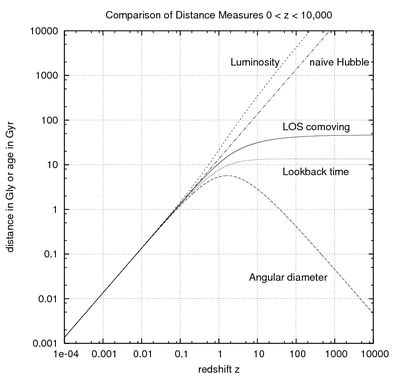

 결합 및 각 직경의 거리를 나타내기 위해 사용됩니다.때때로 광이동 거리는 "눈길 거리" 및/또는 "눈길 시간"[
결합 및 각 직경의 거리를 나타내기 위해 사용됩니다.때때로 광이동 거리는 "눈길 거리" 및/또는 "눈길 시간"[ , 반대 방향으로 멀리 있는 물체는 약 1.0012배
, 반대 방향으로 멀리 있는 물체는 약 1.0012배  결합 거리가 우주의 팽창을 설명하므로 시간에 따라 변하지 않습니다.결합 거리는 시선(LOS)을 따라 가까운 기본 관측자의 적절한 거리를 통합함으로써 얻을 수 있는 반면, 적절한 거리는 일정한 우주 시간에서의 측정치가 산출하는 값이다.
결합 거리가 우주의 팽창을 설명하므로 시간에 따라 변하지 않습니다.결합 거리는 시선(LOS)을 따라 가까운 기본 관측자의 적절한 거리를 통합함으로써 얻을 수 있는 반면, 적절한 거리는 일정한 우주 시간에서의 측정치가 산출하는 값이다. 

 경우 스케일 팩터를
경우 스케일 팩터를
![{\displaystyle d_{C}(z)=d_{H}\Omega _{m}^{-1/3}\Omega _{\Lambda }^{-1/6}[f((1+z)(\Omega _{m}/\Omega _{\Lambda })^{1/3})-f((\Omega _{m}/\Omega _{\Lambda })^{1/3})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b410fcf996358270541d9394cef6750c721e67f)


 분리된 일정한 적색 편이
분리된 일정한 적색 편이 
 적절한 값입니다
적절한 값입니다



 알고 있는
알고 있는 



 측정된 적색편이를 사용해야 하며
측정된 적색편이를 사용해야 하며

 물체에서 관찰자에게 빛이 도달하는 데 걸린 시간과 빛의
물체에서 관찰자에게 빛이 도달하는 데 걸린 시간과 빛의 
 경우, z
경우, z







