기계유사식

수학에서 기계와 같은 공식은 to를 많은 자릿수로 계산하는 데 널리 사용되는 기법이다.1706년 John Machin의 공식은 다음과 같습니다.

(\displaystyle\frac{pi}{4}=4\arctan{frac{1}{5}-\arctan{239})

소수점 100자리까지 ^[1] $100$ 를 계산하곤 했죠

기계와 유사한 공식은 다음과 같은 형태를 가집니다.

c_{0}{\frac {pi }{4}=\sum _{n=1}^{N}c_{n}\arctan {frac {a_{n}}{b_{n}}}}

(1)

$a_{n}$ 서 n $(\$ $b_{n}$ $(\$ $n$ })은 $b_{n}$ 양의 정수입니다. $c_{0}$ $a_{n}<b_{n}$ $a_{n}<b_{n}$ \ $displaystyle$ a _ { n $}$ < b $a_{n}<b_{n}$ _ { $a_{n}<b_{n}$ n $a_{n}<b_{n}$ , $c_{n}$ c $c_{n}$ \ $displaystyle c _$ { n } 은 $c_{n}$ $c_{0}$ 부호 없는 정수, $c_{0}$ 0 \ $displaystyle$ c _ { $0$ } 은 양의 정수입니다.

다음 공식은 arctangent에 대한 Taylor 시리즈 확장과 함께 사용됩니다.

\arctan x=\sum _{n=0}^{\infty}{\frac {(-1)^{n+1}x^{2n+1}=x-{\frac {x^{3}}{{3}}+{\frac {5}-{\frac {7}}}+{\frac {7}}}{{{\frac}}}}}}}}}}{{{{{\frac}}}}}}}}}}}}}}}}}}}}}}}}}}}}}

(2)

파생

아크탄젠트에 대한 각도 덧셈 공식은 다음과 같이 주장한다.

({displaystyle \arctan {a_{1}}{b_{1}}+\arctan {frac {a_{2}}{b_{2}=\arctan {a_{2}+a_{2}b_{1}{b_{1}}-{1}{1}}-{2}}_a})

(3)

한다면

({displaystyle - {\frac {a_{1}} {b_{1}} + {\frac {a_{2}} {b_{2}} <\frac {pi } {2}).}

식 3을 반복 적용함으로써 모든 기계 양식을 도출할 수 있다.예를 들어 Machin의 원래 공식 1의 파생은 다음과 같습니다.

({displaystyle} {frac {1} {5} &= arctan {frac {1} {5} + arctan {frac {1} {1+1\cdot 5} {5\cdot 5} {5\cdot 5} {5\cdot 1\cdot 1\cdot 1\cdot 1\cdot 1\cdot 1\cdot 1\cdot 1\cdot 1\cdot 1\cdot 1\cdot 1\cdot 1\cdot 1\cdot 1} =

결과, ★★★★★★★★★★★★★★★★★★★★」

(*displaystyle {frac {1} {5} &= 2 arctan { frac {1} {5} + 2 arctan { frac {5} + = arctan { frac {5} {12} + arctan {frac {5} {12} \ = arctan { frac5} )\end { aligned}}

''도 마찬가지입니다''

{\displaystyle{\begin{정렬}4\arctan{\frac{1}{5}}-{\frac{\pi}{4}}&=4\arctan{\frac{1}{5}}-\arctan{\frac{1}{1}}\\&,=4\arctan{\frac{1}{5}}+\arctan{\frac{)}{1}}\\&,=\arctan{\frac{120}{119}}+\arctan{\frac{)}{1}}\\&,=\arctan{\frac{120\cdot 1+())\cdot 119}{119\cdot 1-120\cdot())}}\\&,=\arctan{\frac{1}{239}},\end.{정렬}}}

{\frac {pi }{4}=4\arctan {\frac {1}{5}-\arctan {239}.

방정식 3을 시각화하는 통찰력 있는 방법은 두 개의 복소수를 곱하면 어떻게 되는지 상상하는 것입니다.

(b_{1}+a_{1}\mathrm {i})\cdot (b_{2}+a_{2}\mathrm {i})

{1}+displaystyle =b_{1}b_{2}+a_{1}b_{1}\mathrm {1}+mathrm {i}

1}1}displaystyle =(1}{2}-a_{1}_{1}+{1}{1}{1}_a}{b_1}+(a)_1})

(4)

복소수 $(b_{n}+a_{n}\mathrm {i} )$ n + $(b_{n}+a_{n}\mathrm {i} )$ $(b_{n}+a_{n}\mathrm {i} )$ i $){displaystyle (b_{n}+a_{n}\mathrm {i})}$ 과 $(b_{n}+a_{n}\mathrm {i} )$ (와) 관련된 각도는 다음과 같습니다.

({displaystyle\arctan{a_{n}}{b_{n}})

따라서 방정식 4에서 제품과 관련된 각도는 다음과 같습니다.

\arctan {a_{1}b_{2}+a_{2}b_{1}{b_{2}-a_{1}a_{2}}

이것은 방정식 3과 같은 식입니다.따라서, 방정식 3은 두 복소수를 곱하는 것은 관련된 각도를 더하는 것을 의미한다고 해석할 수 있다. (복소수 곱셈 참조)

표현:

{displaystyle c_{n}\arctan {frac {a_{n}}{b_{n}}}}

는 다음과 관련된 각도입니다.

(b_{n}+a_{n}\mathrm {i})^{c_{n}

식 1은 다음과 같이 다시 쓸 수 있습니다.

k\cdot (1+\mathrm {i})^{c_{0}=\display_{n=1}^{N}(b_{n}+a_{n}\mathrm {i})^{c_{n}}

$k$ 서 k $(\displaystyle$ k $)$ 는 $k$ 방정식의 양쪽에 있는 벡터 사이의 크기 차이를 설명하는 임의의 상수입니다.크기는 무시할 수 있으며 각도만 유의합니다.

복소수 사용

복소수를 사용하여 다른 수식을 생성할 수 있습니다.예를 들어 복소수 $(a+b\mathrm {i} )$ + b $)$ 의 각도({displaystyle $(a+b\mathrm {i})$ 는 $(a+b\mathrm {i} )$ $\arctan {\frac {b}{a}}$ $\arctan {\frac {b}{a}}$ a { $displaystyle\arctan\frac {b}{a}})$ 로 $\arctan {\frac {b}{a}}$ 나타내며, 복소수를 곱하면 그 각도를 더한다.a $a=b$ $({displaystyle$ a $=b})$ 이면 $a=b$ $\arctan {\frac {b}{a}}$ $\arctan {\frac {b}{a}}$ a $(\$ 는 $\arctan {\frac {b}{a}}$ 45도 또는 4 $(\$ ${\frac {\pi }{4}}$ 입니다 $\frac{\pi}{4}$ .즉, 실제 부분과 복소 부분이 같을 경우 아크탄젠트는 ${\frac {\pi }{4}}$ ({ $displaystyle\frac\pi}{4$ 가 됩니다.1의 아크탄젠트는 수렴 속도가 매우 느리기 때문에 곱하면 실제 부분과 가상의 부분이 같아집니다.예를 들어 ( $(2+\mathrm {i} )$ + $)$ { $style (2+\mathrm {i})$ $(3+\mathrm {i} )$ 및 $(2+\mathrm {i} )$ ( $)$ { $displaystyle (3+\mathrm {i$ 입니다 $(2+\mathrm {i} )$ 이것들을 곱하면 ( $5\mathrm {i})$ style $(5+$ 5\mathrm {i $(5+5\mathrm {i} )$ 이 됩니다.따라서 $\arctan {\frac {1}{2}}+\arctan {\frac {1}{3}}={\frac {\pi }{4}}$ 1 $\arctan {\frac {1}{2}}+\arctan {\frac {1}{3}}={\frac {\pi }{4}}$ + $\arctan {\frac {1}{2}}+\arctan {\frac {1}{3}}={\frac {\pi }{4}}$ 1 $\arctan {\frac {1}{2}}+\arctan {\frac {1}{3}}={\frac {\pi }{4}}$ $\arctan {\frac {1}{2}}+\arctan {\frac {1}{3}}={\frac {\pi }{4}}$ $4$ 4 $\arctan {\frac {1}{2}}+\arctan {\frac {1}{3}}={\frac {\pi }{4}}$ （ \ displaystyle \ $arctan$ \ $frac$ { ${$ } { } + \ $arctan$ \ $frac$ { $\arctan {\frac {1}{2}}+\arctan {\frac {1}{3}}={\frac {\pi }{4}}$ } { } = $arctan$ \ $pi$ } { $4$ 。

복소수를 사용하여 ${\frac {\pi }{4}}=4\arctan {\frac {1}{5}}-\arctan {\frac {1}{239}}$ 4 ${\frac {\pi }{4}}=4\arctan {\frac {1}{5}}-\arctan {\frac {1}{239}}$ 4 ${\frac {\pi }{4}}=4\arctan {\frac {1}{5}}-\arctan {\frac {1}{239}}$ 1 ${\frac {\pi }{4}}=4\arctan {\frac {1}{5}}-\arctan {\frac {1}{239}}$ - ${\frac {\pi }{4}}=4\arctan {\frac {1}{5}}-\arctan {\frac {1}{239}}$ 1 ${\frac {\pi }{4}}=4\arctan {\frac {1}{5}}-\arctan {\frac {1}{239}}$ （ $displaystyle$ \ $frac$ { $pi$ } { 4 ） = ${\frac {\pi }{4}}=4\arctan {\frac {1}{5}}-\arctan {\frac {1}{239}}$ 4 $arctan$ { $frac$ { $1 }$ - \ $arctan$ { $239 }$ = 4 arctan { $frac$ { 5 } } = 4 \ frac { frac { frac { 5} } you ${\frac {\pi }{4}}=4\arctan {\frac {1}{5}}-\arctan {\frac {1}{239}}$ you you you you you you you you you you you you you you you you you you you you you you you you you of you if if you you you $(5+\mathrm {i} )^{4}(239-\mathrm {i} )=(1+\mathrm {i} )\cdot 2^{2}\cdot 13^{4}$ $(5+\mathrm {i} )^{4}(239-\mathrm {i} )=(1+\mathrm {i} )\cdot 2^{2}\cdot 13^{4}$ + $(5+\mathrm {i} )^{4}(239-\mathrm {i} )=(1+\mathrm {i} )\cdot 2^{2}\cdot 13^{4}$ ) $(5+\mathrm {i} )^{4}(239-\mathrm {i} )=(1+\mathrm {i} )\cdot 2^{2}\cdot 13^{4}$ ( $(5+\mathrm {i} )^{4}(239-\mathrm {i} )=(1+\mathrm {i} )\cdot 2^{2}\cdot 13^{4}$ $(5+\mathrm {i} )^{4}(239-\mathrm {i} )=(1+\mathrm {i} )\cdot 2^{2}\cdot 13^{4}$ ) $(5+\mathrm {i} )^{4}(239-\mathrm {i} )=(1+\mathrm {i} )\cdot 2^{2}\cdot 13^{4}$ ( $(5+\mathrm {i} )^{4}(239-\mathrm {i} )=(1+\mathrm {i} )\cdot 2^{2}\cdot 13^{4}$ + $(5+\mathrm {i} )^{4}(239-\mathrm {i} )=(1+\mathrm {i} )\cdot 2^{2}\cdot 13^{4}$ ) $(5+\mathrm {i} )^{4}(239-\mathrm {i} )=(1+\mathrm {i} )\cdot 2^{2}\cdot 13^{4}$ $(5+\mathrm {i} )^{4}(239-\mathrm {i} )=(1+\mathrm {i} )\cdot 2^{2}\cdot 13^{4}$ 13 2 $(5+\mathrm {i} )^{4}(239-\mathrm {i} )=(1+\mathrm {i} )\cdot 2^{2}\cdot 13^{4}$ 13 $(5+\mathrm {i} )^{4}(239-\mathrm {i} )=(1+\mathrm {i} )\cdot 2^{2}\cdot 13^{4}$ 4 ( $style$ ( $5$ + \ $mathrm { i$ } )^ $4 =$ ( $1$ + \ $mathrm { i$ } )\ $cdot$ 2 $^{ 2$ \ $cdot$ 13 { $4$ } the $(5+\mathrm {i} )^{4}(239-\mathrm {i} )=(1+\mathrm {i} )\cdot 2^{2}\cdot 13^{4}$ 。실제대로 하면 실수는 $4\arctan {\frac {1}{5}}-\arctan {\frac {1}{239}}={\frac {\pi }{4}}~.$ 이 $4\arctan {\frac {1}{5}}-\arctan {\frac {1}{239}}={\frac {\pi }{4}}~.$ . ${239}} = flac {pi } {4} ~ .}$

레머 측도

기계와 유사한 공식의 계산 효율을 특징짓는 가장 중요한 매개변수 중 하나는 다음과 같이 정의된^[2] 레머 측정이다.

{\it {\lambda }}=\sum _{n=1}^{N}{\frac {1}{\log _{10}(b_{n}/a_{n})}}

{\it {\lambda }}=\sum _{n=1}^{N}{\frac {1}{\log _{10}(b_{n}/a_{n})}}

n

{\it {\lambda }}=\sum _{n=1}^{N}{\frac {1}{\log _{10}(b_{n}/a_{n})}}

=

{\it {\lambda }}=\sum _{n=1}^{N}{\frac {1}{\log _{10}(b_{n}/a_{n})}}

N

{\it {\lambda }}=\sum _{n=1}^{N}{\frac {1}{\log _{10}(b_{n}/a_{n})}}

{\it {\lambda }}=\sum _{n=1}^{N}{\frac {1}{\log _{10}(b_{n}/a_{n})}}

{\it {\lambda }}=\sum _{n=1}^{N}{\frac {1}{\log _{10}(b_{n}/a_{n})}}

( (

b

{\it {\lambda }}=\sum _{n=1}^{N}{\frac {1}{\log _{10}(b_{n}/a_{n})}}

/

{\it {\lambda }}=\sum _{n=1}^{N}{\frac {1}{\log _{10}(b_{n}/a_{n})}}

){

displaystyle {\it

{n }=\

sum _{n=1

}{\

frac

{

1}{\log _{

10}(

b_{

n}/

a_{

n

{\it {\lambda }}=\sum _{n=1}^{N}{\frac {1}{\log _{10}(b_{n}/a_{n})}}

르메르 측도를 최대한 작게 하기 위해서는 아크탄젠트 인수에서 양의 $a_{n}/b_{n}$ $a_{n}/b_{n}$ n $({$ 의 $a_{n}/b_{n}$ 비율을 줄이고 Machin-like 공식의 항 수를 최소화해야 한다.현재 n $=$ { $display a_{n}=1$ }에서 $a_{n}=1$ 가장 작은 것으로 알려진 레머의 측정값은 $\lambda \approx 1.51244$ 로 $인해$ $\lambda \approx 1.51244$ 1. $1444 {display44이다$ Chien-Lih(1997)^[4]는 그의 기계식 공식은 다음과 같다.모든 $a_{n}=1~.$ $a_{n}=1~.$ 가 n $a_{n}=1~.$ 때 기계식 $공식$ 에서 매우 일반적입니다. {{ $n} = 1~.}$

2항 공식

$a_{n}=1$ $a_{n}=1$ n $=$ $(\displaystyle a_{n$ }= $1$ 인 특수한 경우, 두 개의 ^[5]항만 있는 해는 정확히 4개입니다.이것들은

오일러:

(\displaystyle\frac{pi}{4}=\arctan(\frac{1}{2}}+\arctan(\frac {1}{3}))

헤르만:

{\displaystyle\frac{4}=2\arctan\frac{1}{2}-\arctan\frac{1}{7}

Hutton's(또는 Vega's^[5]):

{\displaystyle\frac{4}=2\arctan\frac{1}{3}+\arctan\frac{1}{7}

Machin's:

{\frac {\pi }{4}}=4\arctan {\frac {1}{5}}-\arctan {\frac {1}{239}}

4

{\frac {\pi }{4}}=4\arctan {\frac {1}{5}}-\arctan {\frac {1}{239}}

=

{\frac {\pi }{4}}=4\arctan {\frac {1}{5}}-\arctan {\frac {1}{239}}

{\frac {\pi }{4}}=4\arctan {\frac {1}{5}}-\arctan {\frac {1}{239}}

⁡

{\frac {\pi }{4}}=4\arctan {\frac {1}{5}}-\arctan {\frac {1}{239}}

-

{\frac {\pi }{4}}=4\arctan {\frac {1}{5}}-\arctan {\frac {1}{239}}

1

{\frac {\pi }{4}}=4\arctan {\frac {1}{5}}-\arctan {\frac {1}{239}}

（

displaystyle

）

{\frac {\pi }{4}}=4\arctan {\frac {1}{5}}-\arctan {\frac {1}{239}}

= 4

arctan

{

frac

{

{\frac {\pi }{4}}=4\arctan {\frac {1}{5}}-\arctan {\frac {1}{239}}

1

{\frac {\pi }{4}}=4\arctan {\frac {1}{5}}-\arctan {\frac {1}{239}}

} {

5

} - \

arctan

{ 1 }

239

}

$일반적$ 으로 분자 $a_{n}$ { $n}$ 의 $a_{n}$ 값이 제한되지 않는 경우에는 다른 솔루션이 무한히 많습니다.예를 들어 다음과 같습니다.

({displaystyle {frac } {4} = 22 arctan { frac {1} {28} + \ arctan { frac { 1744507482180368565127} {9864639521006153190241239})

또는

(\displaystyle\frac{pi}{4}=22\arctan(\frac{24478}{873121})+17\arctan(\frac{685601}{6904993)

(5)

예

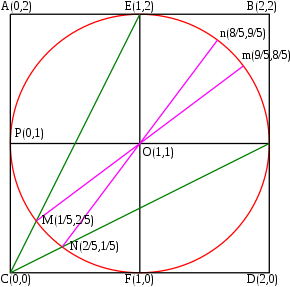
인접한 다이어그램은 아크탄젠트와 해당 영역 간의 관계를 보여줍니다.이 그림에서 다음을 볼 수 있습니다.

{\displaystyle{\begin{배열}{ 주어}{\rm{지역}}(PON)&, ={\rm{지역}}(계기용 변압 변류기)=\pi \times{\frac{MOF\angle}{2\pi}}=\angle MEF=\arctan{1\over 2}\\{\rm{지역}}(달의 변화)&, ={\rm{지역}}(NOF)=\arctan{1\over 3}\\{\rm{지역}}(플라스틱 광 케이블)&, ={\pi \over 4}=\arctan{1\over 2}+\arctan{1\over 3}\\{\rm{지역}}(월요일)&,=\arctan{1\over 7}\\\arctan{1\over 2}&.앰프, =\arctan{1)r 3000+\arctan {1 \over 7},\end {array}}

에 의해서도 찾을 수 있는 관계
복소수 내의 다음 계산

\displaystyle (3+\mathrm {i})(7+\mathrm {i})=21-1+(3+7)\mathrm {i}=10\cdot(2+\mathrm {i})}

더 많은 조건

2002년 $12억4100만엔$ 의 자릿수 기록은 도쿄대학의 야스마사 카나다가 취득했다.계산은 메인 메모리가 1테라바이트인 64노드 Hitachi 슈퍼컴퓨터에서 수행되었으며 초당 2조 번의 연산을 수행했습니다.다음 두 가지 방정식이 모두 사용되었습니다.

{\frac {4}=12\arctan {\frac {1} {4}+32\arctan {\frac {1}{57}-5\arctan {\frac {1}{239}+12\arctan {110443

다카노 기쿠오(1982년).

{\frac {4}=44\arctan {\frac {1} {57}+7\arctan {{239}-12\arctan {\frac {1}{682}+24\arctan {\frac {1}{4}

F. C. M. 슈퇴르메르(1896년)

동일한 결과를 얻을 수 있는지 확인할 수 있도록 두 개의 방정식이 사용됩니다. 방정식이 일부 아크탄젠트를 재사용하지만 모든 아크탄젠트를 한 번만 계산해야 하는 경우에는 유용합니다. 위의 57과 239의 재사용에 유의하십시오.

π에Machin-like 공식이 b2+1의 주요 factorisations 함께 세트에 있는 요소의 개수보단 다음arctan{\display arctangents의 선형 조합 ⁡ 1bn을 건설하는 선형 대수학이나 로렌스 리버모어 연구소 basis-reduction 알고리즘을 사용하여 더 이상 뚜렷한 최고급 제품을 사용한다 숫자를 찾아내 구성될 수 있습니다.s $tyle \arctan {1}{b_{n}}}:$ 정수 $\arctan {\frac {1}{b_{n}}}$ $b_{n}$ $b_{n}$ 의 역수 bn ${$ b_ ${$ n $b_{n}$ 예를 들어, 위의 Störmer 공식의 경우, 우리는

57^{2}+1=2\cdot 5^{3}\cdot 13

239^{2}+1=2\cdot 13^{4}

682^{2}+1=5^{3}\cdot 61^{2}

12943^{2}+1=2\cdot 5^{4}\cdot 13\cdot 61

소수점 2, 5, 13, 61만을 사용하여 네 개의 항을 사용합니다.

1993년 외르크 우베 아른트는^[6] 11항 공식을 발견했다.

{\displaystyle{\begin{정렬}{\frac{\pi}{4}}=&^;36462\arctan{\frac{1}{390112}}+135908\arctan{\frac{1}{485298}}+274509\arctan{\frac{1}{683982}}\\&,-39581\arctan{\frac{1}{1984933}}+178477\arctan{\frac{1}{2478328}}-114569\arctan{\frac{1}{3449051}}\\&,-146571\arctan{\frac{1}{18975991}}+61914\arctan{\frac{1}{22709274}}-6904.4\arctan{\frac {1}{24208144}\&-89431\arctan {1}{201229582}-43938\arctan {frac {1}{2189376182}\\end{aligned}}

11개의 $\{2,5,13,17,29,37,53,61,89,97,101\}.$ 소수점 $\{2,5,13,17,29,37,53,61,89,97,101\}.$ ({ $2, 5$ , $\{2,5,13,17,29,37,53,61,89,97,101\}.$ $\{2,5,13,17,29,37,53,61,89,97,101\}.$ $\{2,5,13,17,29,37,53,61,89,97,101\}.$ $\{2,5,13,17,29,37,53,61,89,97,101\}.$ $\{2,5,13,17,29,37,53,61,89,97,101\}.$ , $\{2,5,13,17,29,37,53,61,89,97,101\}.$ $\{2,5,13,17,29,37,53,61,89,97,101\}.$ 101 $\{2,5,13,17,29,37,53,61,89,97,101\}.$ ({ $displaystyle$ \, 5, $13, 17, 29, 37, 53,$ 61, $89, 97,$ $101$ \})를 사용합니다. $}$

위와 같은 $\displaystyle\arctan}$ 인수 $\arctan$ 중 10개가 Hwang Chien-Lih(2004)에 의해 발견되었으므로 두 인수 모두 동일한 결과를 얻을 수 있는지 확인하는 것이 더 쉽다.

{\displaystyle{\begin{정렬}{\frac{\pi}{4}}=&^;36462\arctan{\frac{1}{51387}}+26522\arctan{\frac{1}{485298}}+19275\arctan{\frac{1}{683982}}\\&,-3119\arctan{\frac{1}{1984933}}-3833\arctan{\frac{1}{2478328}}-5183\arctan{\frac{1}{3449051}}\\&,-37185\arctan{\frac{1}{18975991}}-11010\arctan{\frac{1}{22709274}}+3880\arctan{.\frac{1}{24208144}\&-16507\arctan({1}201229582})\arctan({frac {1}{2189376182}}\\\end{aligned})

이러한 공식은 첫 번째 공식 이후에 동일한 아크탄젠트를 모두 재사용합니다.이들은 $b$ +1이 102보다 작은 소수만으로 나누어질 수 있는 $숫자$ 를² 찾아서 구성됩니다.

$현재$ 알려진 가장 효율적인 기계식 계산식은 다음과 같습니다.

{\frac {pi } {4} = &\frac {1} {239} + 32 \ arctan {\frac {1} {1023} - 68 \ arctan {1} {5832} \ & + 12 \ arctan {\frac {1104

(황천리, 1997)

여기서 소수점 집합은 $\{2,5,13,229,457,1201\}.$ { $\{2,5,13,229,457,1201\}.$ , $\{2,5,13,229,457,1201\}.$ $\{2,5,13,229,457,1201\}.$ $\{2,5,13,229,457,1201\}.$ $\{2,5,13,229,457,1201\}.$ $\{2,5,13,229,457,1201\}.$ 입니다 $.$ {{ $displaystyle \{2,5,13,229,457,$ 1201 $\}.$ $}$

한층 더 개량된 것은,^[3] 에 기재된 「Todd's Process」를 사용하는 것입니다.이것에 의해, 다음과 같은 결과가 초래됩니다.

{\frac {pi } {4} = &\frac {1} {239} + 32 \ arctan {\frac {1} {1023} - 68 \ arctan {1} {5832} \ & + 12 \ arctan { { frac } {\ frac } {\ fractan {\ frac

(황젠리, 2003)

여기서 큰 소수 834312889110521은 마지막 두 지수의 b $+1$ 을_n² 나눈다.
M. Wetherfield 2004 발견

({displaystyle} {\frac {pi } {4} = &\ 83 arctan { frac {1} {1710} + 17 arctan { frac {1} 22 arctan {103697} \ & 24 arctan { frac { 2548} )\\\end {aligned}}

기타 방법

정수의 역수를 사용하여 $\pi$ {\ $displaystyle$ \ $pi}$ 에 $\pi$ 대한 기계식 공식을 도출하는 방법이 있다.하나는 다음 ^[7]공식에 의해 지정됩니다.

{\frac {pi } {4} = 2^{k-1} \ cdot \ arctan _ { frac {1} {A_{k}} + \ sum \ sum _ { m } \ arctan \ frac { 1 } { \ lfloor B _ { \ k , m } { \ fright } \ frac

어디에

a_{0}:=0

재귀적으로

a_{k}:=paramrt {2+a_{k-1}},\;A_{k}=\left\lfloor {frac {a_{k}}{\frecrt {2-a_{k-1}}}\right\loor

그리고.

B_{k,1}: = specfrac {2}{\leftfrac {A_{k}+\mathrm {i}}}{A_{k}-\mathrm {i}}}}\right}^2^{k-1}-\mathrm {i}}}-\mathrmathrm {i}}}

재귀적으로

{\displaystyle B_{k,m}:=frac {1+\left\lfloor B_{k,m-1}\rfloor B_{k,m-1}{\left\lfloor B_{k,m-1}}{\rfloor - B_{k,m-1}}}~}.

예: k $M=5$ $(\displaystyle$ k $=$ $M=5$ $)$ $M=5$ 및 M = $M=5$ 5(\ $displaystyle$ M=5 $)$ 의 $M=5$ 경우 다음을 얻을 수 있습니다.

{\displaystyle{\begin{정렬}{\frac{\pi}{4}}=&^;8\arctan{\frac{1}{10}}-\arctan{\frac{1}{84}}-\arctan{\frac{1}{21342}}\\&,-\arctan{\frac{1}{991268848}}-\arctan{\frac{1}{193018008592515208050}}\\&,-\arctan{\frac{1}{197967899896401851763240424238758988350338}}\\&,-\arctan{\frac{1}{1175738681681753529302777528441941267679.919150085370188369320142936782716885792397}\end {aligned}}

이것은, 다음의 MuPAD 코드로 확인할 수 있습니다.

z:=(10+I)^8*(84-I)*(21342-I)*(991268848-I)*(1930180085925152050-I)\*(19797896405176404242358988350338-I)\117576868686

의미.

{\displaystyle{\begin{정렬}z:=&, \,(10+\mathrm{나는})^{8}\cdot(84-\mathrm{나는})\cdot(21342-\mathrm{나는})\cdot(991268848-\mathrm{나는})\cdot(193018008592515208050-\mathrm{나는})\\&,\cdot(197967899896401851763240424238758988350338-\mathrm{나는})\\&, \cdot(117573868168175352930277752844194126767991915008537018836932014293678271636885792397-\mathrm{i.} \ \ \ ; = & , ( 1 + \ mathrm { i } ) \ cdot \ Re ( z ) ~ . \ end { aligned } }

효율성.

${\$ { $display$ style \ $pi$ $\pi$ 의 대규모 계산에서는 Taylor 시리즈의 용어를 한 번에 하나씩 추가하는 것보다 훨씬 빠르게 이진 분할 알고리즘을 사용하여 아크탄젠트를 계산할 수 있습니다.y-cruncher 등의 실제 구현에서는 term당 일정한 오버헤드가 비교적 크고 1 $1/\log b_{n}$ b n (\ $displaystyle 1/\log b_$ })에 비례하는 시간이 존재하며, 합계에서는 수익률 감소점이 3, 4 아크탄젠트 항을 넘어 나타나기 때문에 위의 슈퍼컴퓨터 계산에서는 4만 사용됩니다.term version 입니다.

특정 알고리즘의 실제 실행 시간을 추정하는 것은 이 섹션의 목적이 아닙니다.대신, 목적은 단지 두 개의 알고리즘을 서로 비교할 수 있는 상대적인 메트릭을 고안하는 것입니다.

$N_{d}$ d { $display style$ N _ { $d$ } $\pi$ 、\ $displaystyle$ \ $pi }$ 를 $\pi$ 계산하는 자리수로 $N_{d}$ .

N $N_{t}$ t { $displaystyle N$ _ { $t$ } be $N_{t}$ 、 Taylor ( ( ( ( (의 항 수를 $N_{t}$ 합니다(식 2 참조).

$($ Taylor 시리즈의 각 용어에 대해) $u_{n}$ 자릿수에 소요된 시간(\ $displaystyle u_{$ n $u_{n}$ })을 지정합니다.

Taylor 시리즈는 다음과 같은 경우에 수렴됩니다.

\displaystyle \left(\leftflac\frac {b_{n}}{a_{n}}\right)^{2}\right)^{N_{t}}=10^{N_{d}}

다음과 같이 됩니다.

({displaystyle N_{t}=N_{d}\quad({frac 10}{2\ln {b_{n}}})

Taylor 시리즈의 첫 번째 항에서는 모든 $N_{d}$ d $\$ 자리가 $N_{d}$ 처리되어야 합니다.그러나 Taylor 시리즈의 마지막 학기에는 처리해야 할 숫자가 한 자리밖에 남지 않았습니다.모든 중간항에서는 선형 보간법에 의해 처리되는 자릿수를 근사할 수 있다.따라서 합계는 다음과 같이 계산됩니다.

{N_{d}N_{t}}{2}

실행 시간은 다음과 같이 지정됩니다.

({displaystyle {mathit {time}}=snfrac {u_{n}N_{d}N_{t}}{2})

방정식을 조합하면 실행 시간은 다음과 같이 지정됩니다.

{{displaystyle {mathit {time}}=mathfrac {u_{d}}^{2}\ln 10}{4\ln {b_{n}}{a_{n}}}=mathfrac {k,u_{n}}{\ln}}}}=mathfrac {b_{n}{n}{n}}}}}}}}}}}}}{{\ln}}}}}}}}}}}

$k$ 서 k $(\displaystyle$ k $)$ 는 $k$ 다른 모든 상수를 합친 상수입니다.이는 상대적인 메트릭이므로k(\ $displaystyle$ k $)$ $k$ 은 $k$ 무시할 수 있습니다.

방정식 1의 모든 항에 걸친 총 시간은 다음과 같습니다.

{{displaystyle {mathit {time}}=\sum _{n=1}^{N}{\frac {u_{n}}{\ln {frac {b_{n}}}{a_{n}}}}}}

$u_{n}$ n \ $display$ style $u_{n}$ : 특정 $u_{n}$ 소프트웨어에 대한 자세한 지식이 없으면 정확하게 모델링할 수 $u_{n}$ .그럼에도 불구하고, 우리는 하나의 가능한 모델을 제시합니다.

소프트웨어는 대부분의 시간을 방정식 2에서 Taylor 시리즈를 평가하는데 소비합니다.프라이머리 루프는 다음 의사 코드로 요약할 수 있습니다.

1:\mathit {term}\display *=\display {a_{n}}^2

(\displaystyle 2:\mathit {term}\display /=\display - {b_{n}}^{2})

(\displaystyle 3:\mathit {tmp}\display =\display {mathit {term}\display /\display (2*n+1)}

(\displaystyle 4:\mathit {sum}\display +=\mathit {tmp})

이 특정 모델에서는 각 단계가 거의 동일한 시간이 걸린다고 가정합니다.사용하고 있는 소프트웨어에 따라서는, 이것은 매우 적절한 근사치이거나, 또는 빈약한 근사치일 수 있습니다.

시간 단위는 의사 코드의 한 단계가 하나의 단위에 대응하도록 정의됩니다.루프를 전체적으로 실행하려면 4단위의 시간이 필요합니다. $u_{n}$ n $\$ 은 $u_{n}$ (는) 4로 정의됩니다.

단, n $(\$ n $a_{n}$ })이 1과 $a_{n}$ 스텝1을 건너뛸 수 있습니다.루프는 3단위의 시간밖에 걸리지 않습니다. $u_{n}$ n $\$ 은 $u_{n}$ 3으로 $u_{n}$ 됩니다.

예를 들어 다음 방정식을 생각해 봅시다.

(\displaystyle\frac{pi}{4}=44\arctan(\frac{74684}{149113})+arctan(\frac{1}{239})-12\arctan(\frac{20138}{15351991})

(6)

다음 표는 각 항의 예상 시간을 보여 줍니다.

$a_{n}$	$b_{n}$	$({displaystyle {b_{n}}}{a_{n}}})$	$(\displaystyle\ln\frac{b_{n}}{a_{n}}})$	$u_{n}$	${mathit {time}$
74684	14967113	200.41	5.3003	4	0.75467
1	239	239.00	5.4765	3	0.54780
20138	15351991	762.34	6.6364	4	0.60274

총 시간은 0.75467 + 0.54780 + 0.60274 = 1.9052입니다.

이것을 방정식 5와 비교하세요.다음 표는 각 항의 예상 시간을 보여 줍니다.

$a_{n}$	$b_{n}$	$({displaystyle {b_{n}}}{a_{n}}})$	$(\displaystyle\ln\frac{b_{n}}{a_{n}}})$	$u_{n}$	${mathit {time}$
24478	873121	35.670	3.5743	4	1.1191
685601	69049993	100.71	4.6123	4	0.8672

총 시간은 1.1191 + 0.8672 = 1.9863입니다.

결론은 이 특정 모형에 기초하여 방정식 6이 방정식 5보다 약간 빠르다는 것입니다. 방정식 6이 더 많은 항을 가지고 있다는 사실과는 무관합니다.이 결과는 일반적인 추세의 전형이다.지배적인 $b_{n}$ 은 n ${$ $displaystyle$ $a_{n$ $}$ 과 $a_{n}$ b{displaystyle $b_{n$ 의 비율인데, 높은 비율을 달성하려면 추가 항을 추가해야 합니다.많은 경우 시간 내에 순절감이 발생합니다.

레퍼런스

^ Beckmann, Petr (1971). A History Of Pi. USA: The Golem Press. p. 102. ISBN 0-88029-418-3.
^ Lehmer, Derrick Henry (1938). "On Arccotangent Relations for π". American Mathematical Monthly. 45 (10): 657–664. doi:10.2307/2302434. JSTOR 2302434.
^ ^a ^b Wetherfield, Michael (2016). "The Enhancement of Machin's Formula by Todd's Process". The Mathematical Gazette. 80 (488): 333–344. doi:10.2307/3619567. JSTOR 3619567.
^ Chien-Lih, Hwang. "More Machin-Type Identities". The Mathematical Gazette. 81 (490). JSTOR 3618793.
^ ^a ^b Carl Størmer (1899). "Solution complète en nombres entiers de l'équation $m\arctan {\frac {1}{x}}+n\arctan {\frac {1}{y}}=k{\frac {\pi }{4}}$ " (PDF). Bulletin de la S.M.F. (in French). 27: 160–170.
^ Jörg Uwe Arndt: "Matters Computational" 섹션 32.5.2, 637페이지.
^ https://arxiv.org/pdf/2108.07718.pdf (표준)

외부 링크

Weisstein, Eric W. "Machin-like formulas". MathWorld.
상수 π
Machin의 MathPages 장점

[1] Beckmann, Petr (1971). A History Of Pi. USA: The Golem Press. p. 102. ISBN 0-88029-418-3.

[2] Lehmer, Derrick Henry (1938). "On Arccotangent Relations for π". American Mathematical Monthly. 45 (10): 657–664. doi:10.2307/2302434. JSTOR 2302434.

[todd-3] Wetherfield, Michael (2016). "The Enhancement of Machin's Formula by Todd's Process". The Mathematical Gazette. 80 (488): 333–344. doi:10.2307/3619567. JSTOR 3619567.

[4] Chien-Lih, Hwang. "More Machin-Type Identities". The Mathematical Gazette. 81 (490). JSTOR 3618793.

[Stormer-5] Carl Størmer (1899). "Solution complète en nombres entiers de l'équation $m\arctan {\frac {1}{x}}+n\arctan {\frac {1}{y}}=k{\frac {\pi }{4}}$ " (PDF). Bulletin de la S.M.F. (in French). 27: 160–170.

[6] Jörg Uwe Arndt: "Matters Computational" 섹션 32.5.2, 637페이지.

[7] ttps://arxiv.org/pdf/2108.07718.pdf (표준)

[1]

[2]

[4]

[5]

[6]

[3]

[7]

Search