메이즈 생성 알고리즘

Maze generation algorithm

미로 생성 알고리즘은 미로를 만드는 자동화된 방법입니다.

이 미로는 프림의 알고리즘을 수정한 것입니다.

그래프 이론 기반 방법

그래프 이론 기반 방법 애니메이션(랜덤화 깊이 우선 검색)

벽면을 사이에 두고 미리 정해진 셀 배열(가장 일반적으로 직사각형 그리드이지만 다른 배열도 가능)부터 시작하여 미로를 생성할 수 있습니다.이 사전 결정된 배열은 가장자리가 가능한 벽 부지를 나타내고 노드가 셀을 나타내는 연결된 그래프로 간주할 수 있다.메이즈 생성 알고리즘의 목적은 2개의 특정 노드 간의 경로를 찾기 어려운 서브그래프를 작성하는 것으로 간주할 수 있습니다.

하위 그래프가 연결되어 있지 않으면 검색 공간에 기여하지 않기 때문에 낭비되는 그래프 영역이 있습니다.그래프에 루프가 포함되어 있는 경우 선택한 노드 사이에 여러 경로가 있을 수 있습니다.이 때문에 메이즈 생성은 랜덤 스패닝트리를 생성하는 것으로 접근되는 경우가 많습니다.루프는 알고리즘 진행 중에 결과에 랜덤 에지를 추가하여 순진한 메이즈 솔버를 혼란시킬 수 있습니다.

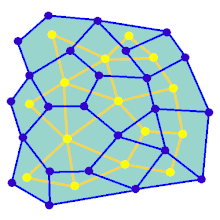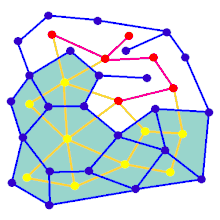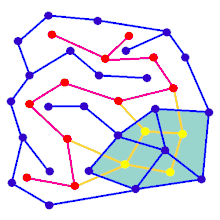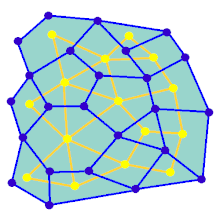
애니메이션은 직사각형 그리드에 없는 그래프에 대한 미로 생성 단계를 보여 줍니다.우선 컴퓨터는 랜덤 평면 그래프 G를 파란색으로, 이중 F를 노란색으로 작성한다.둘째, 컴퓨터는 경로를 빨간색으로 색칠하는 깊이 우선 탐색과 같은 선택된 알고리즘을 사용하여 F를 통과한다.트래버설 중에 빨간색 가장자리가 파란색 가장자리 위로 교차할 때마다 파란색 가장자리가 제거됩니다.마지막으로 F의 모든 정점을 방문하면 F를 지우고 G에서 입구용과 출구용 2개의 엣지를 제거한다.

무작위 깊이 우선 검색

깊이 우선 검색을 이용한 발전기 애니메이션
깊이 우선 검색을 사용한 제너레이터의 다른 애니메이션

"재귀적 역추적" 알고리즘이라고도 하는 이 알고리즘은 깊이 우선 검색 알고리즘의 무작위 버전입니다.

스택과 함께 자주 구현되는 이 접근 방식은 컴퓨터를 사용하여 미로를 생성하는 가장 간단한 방법 중 하나입니다.미로의 공간은 큰 셀 그리드(대형 체스판처럼)이며, 각 셀은 4개의 벽으로 시작합니다.랜덤 셀에서 시작하여 컴퓨터는 아직 방문되지 않은 랜덤 인접 셀을 선택합니다.컴퓨터는 두 셀 사이의 벽을 제거하고 새 셀을 방문한 것으로 표시하고 스택에 추가하여 역추적을 용이하게 합니다.컴퓨터는 이 과정을 계속하여 방문하지 않은 이웃이 없는 셀은 막다른 골목으로 간주됩니다.막다른 골목에서 비방문 네이버 셀에 도달할 때까지 경로를 역추적하여 이 새로운 비방문 셀을 방문함으로써 경로 생성을 계속합니다(새로운 접점을 작성).이 프로세스는 모든 셀이 참조될 때까지 계속되며, 이로 인해 컴퓨터는 처음부터 셀까지 역추적됩니다.우리는 모든 감방을 방문할 수 있습니다.

위에서 설명한 바와 같이 이 알고리즘은 일부 컴퓨터 아키텍처에서 스택오버플로우 문제를 일으킬 수 있는 딥 재귀와 관련되어 있습니다.이 알고리즘은 미로 자체에 역추적 정보를 저장함으로써 루프로 재배열할 수 있습니다.또, 임의의 시점에서 개시해, 최초로 역추적 하는 것으로, 솔루션을 재빠르게 표시할 수 있습니다.

수평 통과 바이어스

깊이 우선 검색으로 생성된 미로는 분기 계수가 낮고 긴 코리더가 많이 포함되어 있습니다.알고리즘은 역추적 전에 각 분기를 따라 가능한 한 멀리 탐색하기 때문입니다.

재귀적 구현

육각형 그리드에서 무작위 깊이 우선 검색

미로 생성의 깊이 우선 탐색 알고리즘은 역추적을 사용하여 자주 구현된다.이는 다음과 같은 재귀 루틴으로 설명할 수 있습니다.

  1. 현재 셀을 매개 변수로 지정
  2. 현재 셀을 방문한 것으로 표시
  3. 현재 셀에는 방문하지 않은 네이버셀이 있는데
    1. 방문하지 않은 이웃 중 하나를 선택합니다.
    2. 현재 셀과 선택한 셀 사이의 벽을 제거합니다.
    3. 선택한 셀에 대해 반복적으로 루틴 호출

지역 내 모든 초기 셀에 대해 한 번 호출됩니다.

반복적인 구현

첫 번째 접근법의 단점은 재귀의 깊이가 크다는 것입니다.최악의 경우 처리 중인 영역의 모든 셀에서 루틴이 반복되어야 하며, 이는 많은 환경에서 최대 재귀 스택 깊이를 초과할 수 있습니다.해결책으로서는 명시적 스택을 사용하여 동일한 백트래킹 방식을 구현할 수 있습니다.이 방법은 통상적으로 큰 폭으로 확장할 수 있습니다.

  1. 첫 번째 셀을 선택하고 방문한 것으로 표시한 후 스택에 푸시합니다.
  2. 스택이 비어 있지 않은 동안
    1. 스택에서 셀을 팝하여 현재 셀로 만듭니다.
    2. 현재 셀에 방문하지 않은 네이버가 있는 경우
      1. 현재 셀을 스택에 푸시합니다.
      2. 방문하지 않은 이웃 중 하나를 선택합니다.
      3. 현재 셀과 선택한 셀 사이의 벽을 제거합니다.
      4. 선택한 셀을 방문한 것으로 표시하고 스택에 푸시합니다.

랜덤화 Kruskal 알고리즘

Kruskal의 알고리즘을 사용하여 30x20 미로를 생성하는 애니메이션.

이 알고리즘은 Kruskal 알고리즘의 랜덤 버전입니다.

  1. 모든 벽의 리스트를 작성하고 각 셀에 대해 세트를 작성합니다.각 셀에는 그 셀이 1개만 포함됩니다.
  2. 각 벽에 대해 임의의 순서로:
    1. 이 벽으로 분할된 셀이 개별 세트에 속하는 경우:
      1. 현재 벽을 제거합니다.
      2. 이전에 분할된 셀 세트를 결합합니다.

셀 세트를 모델링하는 데 사용할 수 있는 몇 가지 데이터 구조가 있습니다.능률적인 실행이 disjoint-set 데이터 구조를 이용하고 2세트에 운영을 거의 지속적으로amortized 시간(특히 O(α(V)){\displaystyle O(\alpha(V))}때에 α())<>){\displaystyle)})의 설득력 있는 값에 대한, runnin하여 각 노조 5{\displaystyle \alpha())<. 5}을 수행할 수 있다gti이 알고리즘의 me는 기본적으로 미로에서 사용할 수 있는 벽의 수에 비례합니다.

벽의 리스트가 처음에 랜덤화 되든, 랜덤하지 않은 리스트에서 랜덤으로 선택되든, 어느 쪽이든 코드화가 간단합니다.

이 알고리즘의 효과는 동일한 가중치를 가진 그래프에서 최소 스패닝 트리를 생성하는 것이기 때문에 해결이 매우 쉬운 규칙적인 패턴을 생성하는 경향이 있습니다.

랜덤화 프림의 알고리즘

프림의 알고리즘을 사용하여 30x20 미로를 생성하는 애니메이션.

이 알고리즘은 Prim 알고리즘의 랜덤 버전입니다.

  1. 벽으로 가득 찬 그리드부터 시작하세요.
  2. 세포를 골라 미로의 일부로 표시해셀의 벽을 벽 목록에 추가합니다.
  3. 목록에 벽이 있는 경우:
    1. 목록에서 임의의 벽을 선택합니다.벽이 분할하는 셀 중 하나만 방문하면 다음과 같이 됩니다.
      1. 벽을 통로로 만들고 방문하지 않은 감방을 미로의 일부로 표시하십시오.
      2. 셀의 인접 벽을 벽 목록에 추가합니다.
    2. 목록에서 벽을 제거합니다.

랜덤 에지 가중치를 가진 그래프에서 고전적인 Prim을 실행하는 것만으로 Kruskal과 스타일적으로 동일한 미로를 만들 수 있습니다. 둘 다 최소 스패닝 트리 알고리즘이기 때문입니다.대신 이 알고리즘은 시작점에 가까운 가장자리의 유효 가중치가 낮기 때문에 스타일 변형을 도입합니다.

수정판

고전적인 Prim 알고리즘은 가장자리 목록을 유지하지만, 메이즈 생성의 경우 인접한 셀 목록을 유지할 수 있습니다.무작위로 선택한 셀에 기존 미로와 연결하는 가장자리가 여러 개 있는 경우 이러한 가장자리 중 하나를 임의로 선택합니다.이는 위의 엣지 기반 버전보다 약간 더 많은 분기가 발생하는 경향이 있습니다.

간이판

알고리즘은 모든 셀 또는 에지의 가중치를 추적하는 것이 아니라 이미 방문한 셀을 무작위로 선택하여 더욱 단순화할 수 있습니다.

보통 시작 셀로 가는 길은 비교적 쉽게 찾을 수 있지만 다른 곳에서는 찾기 어렵습니다.

윌슨 알고리즘

주요 기사:루프 소거 랜덤 워크

위의 모든 알고리즘에는 다양한 종류의 편견이 있습니다. 깊이 우선 검색은 긴 코리더에 치우친 반면, Kruskal/Prim의 알고리즘은 많은 짧은 막다른 골목에 치우쳐 있습니다.반면 Wilson의 [1]알고리즘은 루프 소거 랜덤 워크를 사용하여 모든 미로의 균일한 분포에서 치우치지 않은 표본을 생성합니다.

우리는 임의로 선택된 하나의 셀로 미로를 초기화함으로써 알고리즘을 시작한다.그런 다음 임의로 선택한 새로운 셀에서 시작하여 이미 미로 안에 있는 셀에 도달할 때까지 랜덤 워크를 수행합니다.그러나 임의의 시점에서 랜덤 워크가 자신의 경로에 도달하여 루프를 형성하면 루프가 경로에서 지워집니다.길이 미로에 닿으면 미로에 길을 더하면 돼그런 다음 다른 임의의 시작 셀에서 루프 소거 랜덤 워크를 수행하여 모든 셀이 채워질 때까지 반복합니다.

이 절차는 시작 셀을 임의로 선택하기 위해 어떤 방법을 사용하든 편견 없이 유지됩니다.그래서 우리는 항상 첫 번째 채워지지 않은 셀을 왼쪽에서 오른쪽으로 위에서 아래로 순서대로 선택할 수 있습니다. 단순함을 위해서요.

알더스 브로더 알고리즘

Aldous-Broder 알고리즘도 균일한 스패닝트리를 생성합니다.

  1. 랜덤 셀을 현재 셀로 선택하여 방문한 것으로 표시합니다.
  2. 방문하지 않은 셀이 있는 경우:
    1. 임의의 이웃을 선택합니다.
    2. 선택한 인접 라우터를 방문하지 않은 경우:
      1. 현재 셀과 선택한 인접 셀 사이의 벽을 제거합니다.
      2. 선택한 이웃을 방문한 것으로 표시합니다.
    3. 선택한 네이버를 현재 셀로 만듭니다.

재귀분할법

재귀 분할의 예시
원실 두 벽으로 나누기 벽에 난 구멍 계속 세분화... 완료된
순서 1
순서 2
순서 3
순서 4
순서 5

메즈는 다음과 같이 동작하는 알고리즘인 재귀 나눗셈으로 작성할 수 있습니다.벽이 없는 미로의 공간부터 시작하세요.여긴 방이라고 해챔버를 랜덤하게 배치된 벽(또는 여러 벽)으로 분할합니다. 각 벽에는 랜덤하게 배치된 통로 개구부가 있습니다.그런 다음 모든 챔버의 크기가 최소가 될 때까지 서브 챔버에서 이 과정을 반복하십시오.이 방법은 길고 직선적인 벽이 공간을 가로지르는 미로를 만들어 피해야 할 영역을 쉽게 파악할 수 있게 한다.

예를 들어, 직사각형 미로에서는 서로 수직인 두 개의 벽을 임의의 점에 만듭니다.이 두 개의 벽은 큰 방을 네 개의 벽으로 분리된 네 개의 작은 방으로 나눕니다.네 개의 벽 중 세 개를 무작위로 선택하고 세 개의 벽 각각에서 하나의 셀 폭 구멍을 엽니다.모든 챔버가 두 방향 중 하나의 셀 폭을 가질 때까지 반복하여 이 방법을 계속합니다.

단순한 알고리즘

Prim 알고리즘의 3D 버전입니다.수직 레이어에는 아래에서 위로 1~4의 라벨이 붙어 있습니다.위 계단은 "/", 아래 계단은 "\", 아래 계단은 "x"로 표시됩니다.이미지 설명에 소스 코드가 포함되어 있습니다.

2D 미로의 한 줄 또는 3D 미로의 한 평면을 저장하기에 충분한 메모리만 필요한 다른 알고리즘도 있습니다.Eller 알고리즘은 현재 행의 어떤 셀이 이전 행의 셀을 통해 연결되어 있는지 저장함으로써 루프를 방지하고 이미 [2]연결되어 있는2개의 셀 사이의 벽을 삭제하지 않습니다.Sidewinder 알고리즘은 맨 위 행 전체를 따라 열린 경로로 시작하여 후속 행은 위의 경로와 연결된 짧은 수평 경로로 구성됩니다.Sidewinder 알고리즘은 상향 [3]막다른 골목도 없기 때문에 아래에서 위로 푸는 것은 간단하다.시작 너비가 주어진다면 두 알고리즘 모두 무제한 높이의 완벽한 미로를 만듭니다.

대부분의 미로 생성 알고리즘은 최종 결과를 해결할 수 있도록 그 안에 있는 셀 간의 관계를 유지해야 합니다.그러나 단순히 연결된 유효한 미로는 각 셀에 독립적으로 초점을 맞추어 생성할 수 있습니다.바이너리 트리 미로는 표준 직교 미로이며, 각 셀은 항상 위로 또는 왼쪽으로 이어지는 통로를 가지지만 둘 다 가질 수 없습니다.바이너리 트리 미로를 만들려면 셀마다 동전을 던져 위로 이동할지 왼쪽으로 이동할지 결정합니다.항상 경계상의 셀에 대해 같은 방향을 선택하면 최종 결과는 왼쪽 상단 모서리가 뿌리가 있는 바이너리 트리처럼 보이는 유효한 단순 연결된 미로가 됩니다.Sidewinder와 마찬가지로 바이너리 트리 미로는 편향된 방향으로 막다른 골목은 없습니다.

코드를 사용하여 코모도어 64 BASIC에서 생성된 메이즈10 PRINT CHR$(205.5+RND(1)); : GOTO 10

각 셀에 동전을 던지는 관련 형태는 슬래시와 백슬래시 문자를 임의로 혼합하여 이미지를 만드는 것입니다.이는 단순히 연결된 유효한 미로를 생성하는 것이 아니라 닫힌 루프와 유니커설 통로를 선택하는 것입니다.Commodore 64의 설명서는 보다 부드러운 그래픽 모양을 위해 PETSCII 대각선 그래픽 문자를 대신 사용하여 이 알고리즘을 사용하는 BASIC 프로그램을 제공합니다.

셀룰러 오토마톤 알고리즘

특정 유형의 셀 오토마타를 사용하여 [4]미로를 생성할 수 있습니다.이러한 셀룰러 오토마타로서 잘 알려진 Maze와 Mazectric은 룰스트링 B3/S12345와 B3/[4]S1234를 가지고 있다.전자에서, 이것은 세포가 적어도 한 세대에서 다섯 개의 이웃을 가지고 있다면 다음 세대로 생존한다는 것을 의미한다.후자의 경우, 이것은 세포가 1개에서 4개의 이웃을 가지면 살아남는다는 것을 의미한다.만약 세포에 정확히 세 개의 이웃이 있다면, 그 세포는 태어난다.이는 콘웨이의 게임 오브 라이프와 비슷한데, 어떤 세대에서도 1, 4, 또는 5개의 살아있는 세포에 인접한 살아있는 세포가 없는 패턴은 [4]콘웨이와 동일하게 동작한다.그러나 큰 패턴의 경우 [4]Life와 매우 다르게 동작합니다.

무작위로 시작하는 패턴의 경우, 이러한 미로 생성 셀 오토마타는 복도를 따라 잘 정의된 벽이 있는 복잡한 미로로 진화합니다.규칙 B3/S1234를 가진 Mazecetric은 규칙 B3/S12345와 [4]비교하여 길고 직선적인 회랑을 생성하는 경향이 있습니다.이러한 셀 오토마톤 규칙은 결정론적이기 때문에 생성된 각 미로는 랜덤 시작 패턴에 의해 고유하게 결정됩니다.미로는 비교적 예측하기 쉬운 경향이 있기 때문에 이것은 중대한 결점입니다.

위에서 설명한 그래프 이론 기반 방법 중 일부와 마찬가지로, 이러한 셀 오토마타는 일반적으로 단일 시작 패턴에서 미로를 생성합니다. 따라서 일반적으로 시작 셀로 가는 길은 비교적 쉽게 찾을 수 있지만 다른 곳에서는 찾기 어렵습니다.

「 」를 참조해 주세요.

레퍼런스

  1. ^ Wilson, David Bruce (May 22–24, 1996). "Generating random spanning trees more quickly than the cover time". Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing. Symposium on Theory of Computing. Philadelphia: ACM. pp. 296–303. CiteSeerX 10.1.1.47.8598. doi:10.1145/237814.237880. ISBN 0-89791-785-5.
  2. ^ Jamis Buck (29 December 2010). "Maze Generation: Eller's Algorithm".
  3. ^ Jamis Buck (3 February 2011). "Maze Generation: Sidewinder Algorithm".
  4. ^ a b c d e Nathaniel Johnston; et al. (21 August 2010). "Maze - LifeWiki". LifeWiki. Retrieved 1 March 2011.

외부 링크