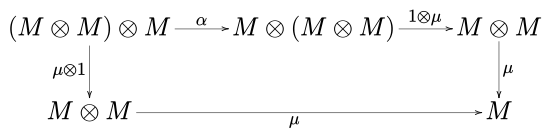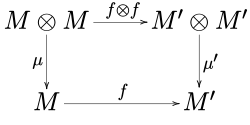모노이드(범주론)

범주론에서 수학의 한 가지, 단조(또는 단조형 물체, 또는 단조형 물체, 또는 내적 단조형, 대수형) (M, μ, η)은 두 가지 형태론과 함께 개체 M이다.

• μ: M ⊗ M → 곱셈이라 불리는 M,
• 例:I → M호출 단위,

오각형 도표처럼.

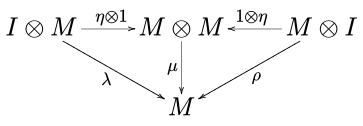
그리고 단조도

통근하다위의 표기법에서 1은 M의 정체성 형태론이고, 나는 단위 원소, α, λ, ρ은 각각 연관성, 왼쪽 정체성, 오른쪽 정체성이다.

단면체 범주 C의 코모노이드(단면체^op 범주 C)는 이중 범주 C의 모노이드(단면체)이다.

단면체 범주 C에 대칭 has이 있다고 가정한다.C의 모노이드 M은 μ o γ = μs일 때 역순이다.

예

• 세트(카르테시안 제품에서 유도된 단면체 구조와 함께)의 범주인 세트의 모노이드 물체는 통상적인 의미에서 단면체다.
• 위상공간(제품 위상에 의해 유도된 단상구조)의 범주인 위상공간(Top)의 모노이드 물체는 위상적 단상이다.
• 모노이드의 범주(모노이드의 직접적인 산물이 있는)에 있는 모노이드 물체는 단지 서로 교환하는 모노이드일 뿐이다.이것은 에크만-힐튼의 주장에서 쉽게 따라온다.
• 완전 조인-세밀릿수 Sup(카르트 제품에서 유도된 단일 구조로 된) 범주에 있는 모노이드 물체는 유니탈 퀀텀이다.
• 아벨 그룹의 범주인 (Ab, ⊗,_Z Z)에 있는 모노이드 물체는 고리다.
• 정류 링R의 경우, 단조로운 물체는
  • R에 대한 모듈 범주(R-Mod, ⊗,_R R)는 R-알지브라이다.
  • 등급이 매겨진 모듈의 범주는 등급이 매겨진 R-알지브라다.
  • R-모듈의 체인 콤플렉스의 범주는 차등 등급 대수다.
• K-벡터 공간의 범주인 K-Vect의 모노이드 물체(Again, 텐서 제품과 함께)는 K-algebra이고, 코모노이드 물체는 K-collgebra이다.
• 범주 C에 대해, 그 엔드포넌트의 범주 [C,C]는 구성과 아이덴티티 펑터 I에_C 의해 유도된 단면 구조를 가지고 있다.[C,C]의 모노이드 물체는 C의 모노이드 물체다.
• 유한한 제품을 가진 모든 범주의 경우, 모든 개체는 대각선 ${\displaystyle {형태론}_{}\Delta }$ X : ${\displaystyle X}$ → ${\displaystyle X}$ $×$X {\$displaystyle$ \$Delta$ _${X}$를 통해 코모노이드 객체가 된다.$X\to X\times$X$\}.$ coproducts가 유한한 범주에서 모든 객체는 $i{\displaystyle }$ ${\displaystyle d_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle i_{}}$ : ${\displaystyle X}$ : ${\displaystyle X{}_{}\bigsqcup }$ ${\displaystyle X}$→ X ${\displaystyle id_{X}\sqcup id_{X}:X\sqcup$X$\to$ X$}$를 통해 단일 객체가 된다$.$

모노이드의 범주

모노이드 범주 C에서 2개의 모노이드(M, μ, μ, μ')와 (M', μ', η')를 볼 때, 형태론 f : M → M '는 모노이드의 모노이드의 형태론이다.

• f o μ = μ' o(f μ f),
• f o η = η'이다.

즉, 다음 도표

,

통근하다

C에 있는 모노이드와 그 모노이드 형태론의 범주는 Mon이라고_C 쓰여 있다.^[1]

참고 항목

• Act-S, 세트에 작용하는 모노이드의 범주

참조

• 마티 킬프, 울리히 크나워, 알렉산더 5세Mikhalov, Monoids, Acts and Categories(2000), Walter de Gruyter, Berlin ISBN 3-11-015248-7