핵오버하우저 효과

핵 오버하우저 효과(NOE)는 스핀 활성 핵의 한 모집단(예: H, C, N 등)에서 교차 완화를 통해 다른 모집단으로 핵 스핀 분극이 전달되는 것이다.핵자기공명분광학(NMR)에서 NOE의 현상학적 정의는 RF장 조사에 의해 다른 NMR 공명이 포화되었을 때 발생하는 하나의 NMR 공명의 통합 강도(양 또는 음)의 변화이다.핵의 공진 강도 변화는 핵이 RF 섭동의 직접적인 영향을 받는 핵과 공간적으로 가깝기 때문이다.

NOE는 NMR 공명의 할당, 유기 및 생물학적 분자의 구조 또는 구성의 설명과 확인에 특히 중요하다.H 2차원 NOE SpectroopY(NOESY) 실험과 그 확장은 용액에서 단백질과 다른 생체 분자의 입체 화학을 식별하기 위한 중요한 도구인 반면, 고체 형태의 결정 X선 회절은 일반적으로 ^[1]입체 화학을 식별하기 위해 사용된다.^[2] ^[3] 이종핵 NOE는 양성자에 결합하는 탄소를 식별하고, 신호 대 잡음을 증가시키기 위해 그러한 탄소에 분극 개선을 제공하며, 이러한 탄소의 완화가 쌍극자-다이폴 완화 ^[4]메커니즘에 의해 제어되는 정도를 확인하기 위해 C NMR 분광학에서 특히 중요하다.

역사

NOE는 1953년 특정 ^[5]금속의 전도 전자의 극초단파 조사에 의해 핵 스핀 분극이 강화될 수 있다고 제안한 미국의 물리학자 앨버트 오버하우저의 이론 연구에서 발전했다.오버하우저가 예측한 전자핵 증강은 1953년 T. R. Carver와 C. P. Slichter에 의해 Li 금속에서 실험적으로 입증되었다.^[6] HF 분자의 핵 스핀만을 포함하는 오버하우저 효과에 대한 일반적인 이론적 근거와 실험적인 관찰은 1955년 ^[7]이오넬 솔로몬에 의해 발표되었다.1963년 카이저는 NOE의 또 다른 초기 실험 관찰을 사용하여 스칼라 결합 상수의 상대적 신호를 결정하고 에너지 수준 간 전환에 NMR 스펙트럼의 스펙트럼 라인을 할당하는 방법을 보여주었다.이 연구에서, 동일한 유기 분자의 두 번째 개별 양성자 집단이 ^[8]RF 조사에 의해 포화되었을 때 유기 분자의 ¹한 양성자 집단(H)의 공명이 향상되었다.NOE의 적용은 1965년 Anet과 Bourn에 의해 β, β-디메틸 아크릴산 및 디메틸 포름아미드에 대한 NMR 공명의 할당을 확인하기 위해 사용되었으며, 이를 통해 용액 내 유기 분자에 대한 구성 및 구성 정보를 얻을 수 있음을 보여주었다.^[9] 벨과 손더스는 1970년에 NOE 향상과 핵간 거리 사이의 직접적인 상관관계를 보고한 반면, 3회 이상의 스핀을 가진 분자의 핵간 거리에 대한 정량적 측정이 쉬르머 외 연구진에 의해 보고되었다.^[11]

리처드 R. 에른스트는 푸리에 변환과 2차원 NMR 분광학을 개발한 공로로 1991년 노벨 화학상을 수상했으며, 이는 곧 NOE, 특히 큰 생물학적 ^[12]분자의 측정에 적용되었다.2002년, Kurt Wuthrich는 수용액에서 생물학적 고분자의 3차원 구조를 결정하여 핵자기공명분광학 개발로 노벨 화학상을 수상하였으며, 2D NOE법(NOESY)을 사용하여 대형 생물학적 ^[13]고분자의 3차원 구조를 제한하는 방법을 증명하였다.아닐 쿠마르 교수는 생체분자에 ^[14]2차원 핵과잉효과(2D-NOE, 현재 NOESY로 알려져 있음) 실험을 최초로 적용하여 NMR 분광법에 의한 용액 내 생체분자의 3차원 구조를 결정하는 장을 열었다.

릴렉스

2 스핀에 대한 핵 스핀 에너지 수준 다이어그램1/2개의 핵.^[3]

H NOE 실험을 위한 정상 상태 펄스 시퀀스

NOE와 핵 스핀-래티스 완화는 밀접하게 관련된 현상이다.자기장 내 단일 스핀-1 nucleus2 핵에 대해 종종 α와 β로 표기되는 두 가지 에너지 레벨이 있으며, 각각 +122와 -122의 가능한 스핀 양자 상태에 대응한다.열평형에서 두 에너지 레벨의 모집단은 P와_β P에 의해_α 주어진 스핀 모집단과 함께 볼츠만 분포에 의해 결정된다.스핀 모집단이 전환 에너지 주파수에서 적절한 RF장에 의해 교란되면 스핀 모집단은 스핀-라티스 완화라고 불리는 프로세스에 의해 열 평형으로 돌아갑니다.α에서 β로의 이행 속도는 상태 α, P의_α 모집단에 비례하며 속도 상수 W를 갖는 1차 과정이다.연속적인 RF 조사(P = P)에_α_β 의해 스핀 모집단이 균등해지는 상태를 포화라고 하며 전이 확률은 에너지 수준 간의 모집단 차이에 따라 달라지기 때문에 공명이 사라진다.

NOE가 관련된 가장 단순한 경우, 2개의 스핀-1 nuclei2 핵, I와 S의 공명은 화학적으로 이동하지만 J결합은 아니다.이러한 시스템에 대한 에너지 다이어그램은 각각 αα, αβ, βα 및 β에 해당하는 I 및 S의 스핀 상태에 따라 달라지는 4가지 에너지 레벨을 가진다.W는 네 가지 에너지 수준 사이에서 전환이 발생할 단위 시간 당 확률 또는 다른 측면에서 해당 스핀 플립이 발생하는 속도입니다.αα β 및 αβ β에 대응하는₁^S W, αα β 및 βα β에 대응하는 W, βα β에 대응하는 제로 양자 전이 W₀, βα ββ에 대응하는 이중 양자 전이가 있다₁^I.

RF 조사는 관측 가능한 스펙트럼 라인을 생성하는 단일 양자 전이를 유도할 수 있지만(이른바 양자 역학 선택 규칙에 의해) 쌍극자 완화는 모든 경로를 통해 발생할 수 있다.이중극 메커니즘은 하나 이상의 스핀 플립이 발생하는 전환을 일으킬 수 있는 유일한 일반적인 완화 메커니즘입니다.구체적으로는 αα와 ββ 상태(W₂) 간 및 αβ와 βα 상태(W₀) 간 전이를 발생시킨다.

핵 S의 공진이 포화 $M_{S}=0$ 일 때 핵 $M_{S}=0$ 에 대해 실험적으로 관찰된 정상 상태 NOE( $M_{S}=0$ S $=$ 0 \ $displaystyle M_{S$ }= $0$ )는 다음과 같이 정의된다.

\displaystyle \eta _{I}^{S}=\left({\frac {M_{I}^{S}-M_{0)I}}{M_{0}I}}}\right)}

$M_{0I}$ 서 M 0 $M_{0I}$ { $displaystyle M$ _ { $0$ }I $}}$ 은 $M_{0I}$ 열평형상태에서 $(\$ displaystyle $I)$ 의 자화 $I$ (공진강도)입니다.NOE에 대한 분석식은 모든 완화 경로를 고려하고 솔로몬 방정식을 적용하여 얻을 수 있다.

\eta _{I}^{S}=black {M_{I}^{S}-M_{0}I}}{M_{0}I}}=frac_{S}{\gamma_{I}}{\frac_{frac_{IS}}{\rho _{I}}=hargfrac {\gamma _{I}}\left({\frac {W_{2}-W_{0}}){2}W_{1}^{I}+W_{0}+W_{2}}\right)

어디에

\rho _{I}=2W_{1}^{I}+W_{0}+W_{2}

W_{0}+W_{2}}

및

\rho _{I}=2W_{1}^{I}+W_{0}+W_{2}

\sigma _{IS}=W_{2}-W_{0}

\sigma _{IS}=W_{2}-W_{0}

S

\sigma _{IS}=W_{2}-W_{0}

\sigma _{IS}=W_{2}-W_{0}

2 -

\sigma _{IS}=W_{2}-W_{0}

(\

display style

\

display

_

\sigma _{IS}=W_{2}-W_{0}

)

IS}=W_{2}-W_{0

$\rho _{I}$ $I$ ( \ $displaystyle$ \ $rho$ _ { I $\rho _{I}$ } )는 스핀 s, $i$ I $\sigma _{IS}$ ( \ $displaystyle$ $1/T_{1}$ \ $sigma$ _ )의 존재로 인한 스핀 I의 총 세로 방향 쌍극자 $1/T_{1}$ ( $1/T_{1}$ / $T$ $1/T_{1}$ ( \ $displaystyle$ 1/ $T_$ { $1/T_{1}$ } ) $IS}$ 를 $\sigma _{IS}$ 교차완화율이라고 하며 $,$ $\gamma _{S}$ I \ display $style$ \ $gamma _$ { I $\gamma _{I}$ $},$ ② S \ display style $I$ \ $gamma$ _ ${$ $S}$ 는 $\gamma _{S}$ $S$ $각각$ I \ display $style$ I $},$ $S$ \ $display$ S $핵$ 의 특성 자기비이다.

축퇴된₁^S W 전이의 포화는 평형 모집단을 교란시켜 P = P_αβ, P_βα = P가_ββ 되도록_αα 한다.그러나 시스템의 완화 경로는 활성 상태로 유지되며 평형을 재정립하기 위해 작용한다. 단, 이러한 전환에 걸친 모집단 차이는 RF 조사에 의해 고정되는 반면 W 전환_I 간의 모집단 차이는 평형 값에서 변경되지 않기 때문에 W 전환은₁^S 무관하다.즉, 단일 양자 전이가 완화 경로로 활성화되어 있다면 S $(\displaystyle$ S $)$ $S$ 을 $S$ 포화시켜도 I $(\displaystyle$ I $)$ $I$ 의 $I$ 강도에 영향을 미치지 않습니다.따라서 I의 공진강도에 대한 NOE를 관찰하려면 $W_{0}$ 0 $($ W_ ${0})$ $W_{2}$ $W_{2}$ 2 $($ W_ ${2})$ 의 $W_{2}$ 기여가 중요해야 합니다.교차 완화 경로로 알려진 이러한 경로는 완화가 쌍극자-쌍극자 또는 스칼라 결합 상호작용에 의해 지배될 때만 스핀-락티스 이완에 상당한 기여를 하지만 스칼라 상호작용은 거의 중요하지 않으며 무시할 수 있는 것으로 가정된다.【 $\gamma _{I}=\gamma _{S}$ $=$ $\gamma _{I}=\gamma _{S}$ 】 $\gamma _{I}=\gamma _{S}$ 【 $\gamma _{I}=\gamma _{S}$ 】【 S 】【 $\gamma _{I}=\gamma _{S}$ I 】【 I 】= \ $gamma$ _ { $S$ 】의 경우, $W_{2}$ 2 $W_{2}$ 【 display $style W$ _ {2} $W_{2}$ 】의 $W_{2}$ 경우, S{ $display style$ S】의 $S$ $포화도는$ I= S 【 $display style$ $】$ 의 $I$ $공명$ 강도가 $W_{0}$ 하지만, $NOE$ 는 양수인 $W_{0}$ 는 0이다. $Yle$ W_ ${0}$ 는 $W_{0}$ 주요 완화 경로이며 $,$ S(\ $displaystyle$ S $)$ 를 $S$ $S$ 시키면 I $(\displaystyle$ I $)$ 공명 $I$ $I$ 가 감소하고 NOE가 음수입니다.

분자 운동

NOE가 양인지 음인지 여부는 회전 분자 운동 정도에 민감하게 좌우됩니다.^[3] 세 가지 쌍극 완화 경로는 여러 요인에 따라 스핀-래티스 완화 범위를 달리하는 데 기여한다.중요한 것은 δ₂, δ₁, δ의₀ 균형은 분자가 1라디안을 회전시키는 데 걸리는 시간인 분자 회전 상관 시간 $\tau _{c}$ c $\$ 에 따라 결정적으로 좌우된다는 것이다.NMR 이론은 전이 확률이 $\tau _{c}$ c \ $displaystyle$ \ $tau$ _ { $c$ } 및 $\tau _{c}$ Larmor 세차 주파수 $\omega$ \ $displaystyle$ \ obega $\omega$ 와 관계가 있음을 보여줍니다.

W_{1}^{I}\propto {3\tau _{c}}{(1+\Omega _{I}^{2}\tau _{c}^2}}}{\frac {1}{r^{6}}}

({displaystyle W_{0}\propto {frac {2\tau _{c}}}{(1+(((오메가 _{I}-\오메가 _{S})^{2}}}){\frac {1}{r^6}}}}}}

({displaystyle W_{2}\propto {frac {12\tau _{c}}}{(1+((오메가 _{I}+\오메가 _{S})^{2}}}}) {\frac {1}{r^6}}}}}

$r$ 서 r $\displaystyle$ r은 $r$ 2개의 스핀-1⁄2 핵을 분리하는 거리입니다.이완이 일어나려면 분자 텀블링의 빈도가 핵의 라모르 빈도와 일치해야 한다.이동성 용제에서는 분자 투하운동이 $\omega$ (\ $displaystyle \obe$ 보다 훨씬 빠르다.이 경우 $\omega \tau _{c}\ll 1$ $\omega \tau _{c}\ll 1$ $\omega \tau _{c}\ll 1$ (\ $displaystyle \obe \tau$ _ ${c}\$ 1)이라고 하는 극단적 협소한계이다.이러한 조건에서는, 「와_c₀ 2」가 「」와_c「」보다₁ 일치하기 때문에, W나 W보다₀ 더블₁ 퀀텀 완화₂ W가 효과적이다.γ가₂ 주요 완화 과정일 경우 양의 NOE가 발생한다.

W_{1}^{I}\propto \gamma _{I}^{2}\gamma _{S}^{2}{\frac {3\tau _{c}}{r^{6}}}

\displaystyle W_{0}\propto \gamma _{I}^{2}\gamma _{S}^{2}{\frac {2\tau _{c}}{r^{6}}}}

W_{2}\propto \gamma _{I}^{2}\gamma _{S}^{2}{\frac {12\tau _{c}}{r^{6}}}

_{I}^{S}(최대)=frac {\gamma _{I}}\left[{\frac {12\frac {c}}{r^{6}}-{\frac {2\frac {c}}{{r^6}}}}{\frac {\frc}}}}}}

이 식은 I = S인 동핵의 경우, 특히 H NMR의 경우, 관측할 수 있는 최대 NOE는 핵의 근접성에 관계없이 1\2이다.I s S인 이종핵의 경우, 최대 NOE는 1\2(θ_S/θ_I)로 주어지며, 이는 광대역 양성자 디커플링 조건에서 헤테로핵을 관찰할 때 주요 민감도 개선을 가져올 수 있다.유기화학에서 가장 중요한 예는 J 공명을 포화시키는 H를 디커플링하면서 C를 관찰하는 것이다.δ_S/θ_I 값은 4에 가깝습니다.이 값은 최대 200%의 NOE 강화로 NOE가 없을 때의 3배의 공진을 생성합니다.^[15] 많은 경우에, 탄소 원자는 연결된 양성자를 가지고 있으며, 이로 인해 이완은 쌍극자 이완에 의해 지배되고 NOE는 거의 최대치에 가까워진다.비양성자 탄소 원자의 경우 NOE 강화는 작은 반면, 다이폴-다이폴 상호작용 이외의 완화 메커니즘에 의해 완화되는 탄소의 경우 NOE 강화는 현저하게 감소할 수 있다.이것은 C NMR에서 중수소화 용제(예: CDCl₃)를 사용하는 하나의 동기이다. 중수소는 4극성 메커니즘에 의해 완화되기 때문에 교차 완화 경로가 없으며 NOE는 존재하지 않는다.또 다른 중요한 사례는 N으로, 자기장비의 값이 음의 값이다.종종 N개의 공명이 감소하거나 H핵이 분리될 때 NOE가 실제로 공명을 무효화할 수 있습니다.일반적으로 음의 NOE를 최소화하기 위해 양성자에서 N으로의 편파 전달을 수반하는 펄스 기법으로 그러한 스펙트럼을 취하는 것이 유리하다.

구조 설명

첫 번째 NOE는 아넷과 본에 의해 보고되었습니다.

핵간 거리에 대한 정상 상태 NOE의 관계가 복잡하지만, 완화 속도 및 분자 움직임에 따라 극단적으로 좁은 한계에서 빠르게 떨어지는 작은 분자의 경우, 양의 NOE의 반정량적 특성은 종종 측정값과 함께 많은 구조적 애플리케이션에 유용하다.J-커플링 상수의 ent.예를 들어 NOE 강화는 NMR 공진 할당을 확인하고, 구조 이성질체를 구별하며, 방향족 고리 치환 패턴 및 지방족 치환 구성을 식별하고, 입체구조 ^[3]선호도를 결정하기 위해 사용될 수 있다.

그럼에도 불구하고, 관측된 NOE에서 도출된 원자간 거리는 종종 ^[3]^[15]분자의 3차원 구조를 확인하는 데 도움을 줄 수 있다.이 적용에서 NOE는 화학적 결합이 아닌 공간을 통해 발생한다는 점에서 J 결합의 적용과 다르다.따라서 서로 가까운 원자는 NOE를 얻을 수 있는 반면 스핀 커플링은 원자가 2~3개의 화학적 결합으로 연결되어 있을 때만 관찰된다.그러나 δ_I^S(max)=122 관계는 NOE가 두 핵 I와 S 사이의 쌍극자-쌍극자 상호작용에 의해 100% 완화가 지배되는 이상적인 경우에만 적용되기 때문에 핵간 거리와 어떻게 관련이 있는지 불분명하다.실제로, ρI의 값은 오직 여자 1증가시킴으로써 W0과 W2의 영향력을 축소하는 데 기여하는 다른 경쟁 메커니즘,로부터 공헌들을 포함하고 있다.예를 들어 용매에 녹아 있는 산소를 주거나 상자성 금속 이온 불순물로electron-nuclear 상호 작용 때문에 때로는 편안함 약한 지형 추적 비행 고장의 관측을 금하고 있다.다른 완화 메커니즘의 존재 하에서 관찰된 NOE는 다음과 같이 주어진다.

\displaystyle \eta _{I = frac { frac }IS}}{\rho_{I}+\rho^{*}}}}

여기서 θ는^⋇ 교차 이완을 포함하지 않는 완화 메커니즘의 총 이완 속도에 대한 추가 기여도이다.극단적으로 좁은 한계에서 쌍극자 이완에 대해 동일한 이상적인 2회전 모델을 사용한다.

\displaystyle \rho _{I}\propto {frac _{c}}{r^{6}}

라는 것은 쉽게 알 수 있다

\displaystyle _{I}^{S}\propto \left({\frac {tau _{c}}{\rho ^{*}}\right){\frac {1}{r^{6}}}}}

따라서, 2 스핀 정상 상태 NOE는 외부 이완의 기여가 있을 때만 핵간 거리에 의존한다.Bell과 Saunders는 극단적으로 좁은 ^[10]한계에서 유사한 분자에 대해 엄격한 가정 θ^⋇/θ를_c 따르는 것이 거의 일정하다는 것을 보여주었다.따라서 정상상태 NOE 값의 비율을 취하면 핵간 거리 r에 대한 상대값을 얻을 수 있다.정상상태 실험은 많은 경우에 유용하지만, 상대적인 핵간 거리에 대한 정보만 제공할 수 있다.한편, NOE가 증가하는 초기 속도는 r에_IS⁻⁶ 비례하며, 이는 2D-NOESY와 같은 일시적인 실험을 통해 구조 정보를 얻기 위한 다른 보다 정교한 대안을 제공한다.

2차원 NMR

표준 2차원 NOESY 실험을 위한 펄스 시퀀스

코데인의 2D NOESY 스펙트럼

NOE를 측정하기 위해 2차원 NMR을 사용하는 동기는 다른 2-D 방법과 유사하다.최대 분해능은 영향을 받는 공명을 2차원에 분산시킴으로써 개선되므로 더 많은 피크가 분해되고 더 큰 분자를 관찰할 수 있으며 한 번의 측정으로 더 많은 NOE를 관찰할 수 있다.더 중요한 것은 분자 운동이 NOE가 0이거나 음일 때 중간 또는 느린 운동 상태에 있을 때, 정상 상태의 NOE 실험은 핵간 ^[3]거리와 관련될 수 있는 결과를 제공하지 못한다.

코데인 분자

NOSY(Nuclear Overhauser Effect Spectroscopy)는 교차완화 중인 핵 스핀을 식별하고 교차완화율을 측정하는 데 사용되는 2D NMR 분광법이다.H 쌍극자-다이폴 커플링은 용액 중 유기 분자에 대한 일차적인 교차완화 수단을 제공하기 때문에 교차완화 중인 스핀은 우주에서 서로 가까운 스핀이다.따라서 NOESY 스펙트럼의 교차 피크는 우주에서 서로 가까운 양성자를 나타낸다.이 점에서 NOESY 실험은 스핀-스핀 상관관계를 제공하기 위해 J-커플링에 의존하고 분자의 화학적 결합을 통해 어떤 H가 다른 H에 가까운지를 나타내는 COSY 실험과는 다르다.

기본 NOESY 시퀀스는 3개의 90° 펄스로 구성됩니다.첫 번째 펄스는 횡방향 스핀 자화를 생성합니다.스핀은 진화 시간₁ t 동안 세차되며, 2D 실험 과정에서 증가합니다.두 번째 펄스는 펄스 방향에 직교하는 가로 자화 성분과 동일한 세로 자화를 생성합니다.따라서 혼합기간 θ에_m 대한 초기조건을 생성하는 것이 목적이다.NOE 혼합 시간 동안 교차 완화를 통한 자화 전달이 발생할 수 있습니다.기본적인 NOESY 실험의 경우, δ는_m 2D 실험 내내 일정하게 유지되지만, 최적의 교차 완화율과 NOE 축적을 위해 선택됩니다.세 번째 펄스는 나머지 세로 자화로부터 가로 자화를 생성합니다.제3의 펄스 직후에 데이터 수집이 개시되어 펄스 지연시간₂ t의 함수로서 횡자화가 관찰된다.NOESY 스펙트럼은 t와₂ t에 대한₁ 2D 푸리에 변환에 의해 생성됩니다.혼합 시간이 증가함에 따라 일련의 실험을 수행하고 NOE 강화의 증가를 뒤따른다.가장 가까운 양성자는 NOE의 가장 빠른 축적 속도를 보여준다.

양성자 간 거리는 교차 피크 강도 분석을 통해 명확하게 할당된 잘 분해된 높은 신호 대 잡음 NOESY 스펙트럼에서 확인할 수 있다.이러한 값은 체적 통합을 통해 얻을 수 있으며, 프로톤 간 거리의 추정치로 변환할 수 있습니다.두 $원자$ $j$ 와 $i$ j $사이$ 의 거리는 크로스 피크 $V$ 와 스케일링 $상수$ c ${displaystyle$ c $}$ 에서 $j$ $V$ 계산할 수 있습니다.

\displaystyle r_{\text{NOE}}=\left({\frac {c}{V_{ij}}}\오른쪽)^{1/6}}

$c$ 서 c $\displaystyle$ c는 $c$ 알려진 고정 거리 측정을 기반으로 결정할 수 있습니다.거리 범위는 스펙트럼 내의 알려진 거리와 부피를 기반으로 보고할 수 있으며, 이는 $평균$ c $\displaystyle$ c\displaystyle c_ ${$ 와 표준 $c$ $c_{SD}$ $\$ {를 나타낸다. $SD$ NOESY 스펙트럼의 여러 영역(노이즈 $V_{\rm {err}}$ r $V_{\rm {err}}$ , {\rm ${err$ 측정값, 즉 $V_{\rm {err}}$ V $r {\rm$ {err}, 측정 오류 $m_{v}$ v $m_{v}$ {\ $displaystyle m_{v$ $파라미터$ x $(\displaystyle$ x $)$ 는 $x$ 알려진 모든 거리가 오차 범위 내에 있도록 설정됩니다.이는 NOESY 볼륨의 낮은 범위를 표시할 수 있음을 나타냅니다.

\displaystyle r_{\text{NOE lower}}=\leftfrac\frac {c-xc_{SD}}{\frac {1}{m_{v}}}V_{ij}+V_{\rm {err}}}}\right)^{1/6}

그리고 상한은

\displaystyle r_{\text{NOE higher}}=\leftfrac\frac {c+xc_{SD}}{\frac {1}{m_{v}}}V_{ij}-V_{\rm {err}}}}\right)^{1/6}

이러한 고정 거리는 연구된 시스템에 따라 달라집니다.예를 들어, 잠긴 핵산은 당에서 거리가 매우 작은 많은 원자를 가지고 있으며, 이를 통해 NMR은 LNA 분자역학 예측을 ^[16]벤치마킹할 수 있었다.그러나 RNA는 훨씬 더 입체적으로 유연한 당을 가지고 있으며,^[17] 하한과 상한의 광범위한 추정을 필요로 한다.

단백질 구조 특성화에서 NOE는 분자 내 거리에 제약을 만들기 위해 사용된다.이 방법에서 각 양성자 쌍은 격리되어 고려되며 NOESY 교차 피크 강도는 쌍둥이자리 메틸렌 양성자 쌍 또는 방향족 고리 양성자와 같은 고정 거리의 양성자 쌍으로부터의 기준 교차 피크와 비교된다.이 간단한 접근법은 스핀 확산 또는 불균일한 상관 시간의 영향에 상당히 둔감하며, 충분한 수의 NOE가 확인되었을 경우 일반적으로 단백질의 전역 접힘을 정의할 수 있다.NOESY 크로스 피크는 강, 중, 약으로 분류할 수 있으며 각각 약 2.5, 3.5, 5.0Ω의 상한 거리 구속으로 해석할 수 있다.그러한 제약조건은 ^[18]분자역학 최적화에 사용되어 단백질의 용액 상태 배열을 파악할 수 있다.전체 구조 결정은 화학적 이동과 NOESY 제약 조건을 모두 활용하는 다양한 NMR 실험과 최적화 방법에 의존합니다.

이종핵 NOE

몇 가지 실험 방법

NOE를 이용하는 1차원 및 2차원 NMR 실험 기법의 예는 다음과 같다.

NOESY, 핵과잉 사용자 효과 분석
HOESY, 헤테로핵오버하우저 효과 분광법
ROESY, 회전 프레임 핵오버하우저 효과 분석
TRNOE, 전이 핵오버하우저 효과
DPFGSE-NOE, 이중 펄스 자기장 경사 스핀 에코 NOE 실험

NOESY는 분자 내 원자의 상대적 방향, 예를 들어 단백질이나 다른 큰 생물학적 분자의 결정으로, 3차원 구조를 생성한다.HOESY는 서로 다른 원소의 원자 사이의 NOESY 교차 상관 관계입니다.ROESY는 일반 NOESY가 적용되지 않는 분자에 적용되는 0이 되는 것을 방지하기 위해 자화를 스핀 잠금하는 것을 포함합니다.TRNOE는 단백질에 대한 리간드 결합에서와 같이 동일한 용액에서 상호작용하는 두 개의 다른 분자 사이의 NOE를 측정합니다.^[19] DPFGSE-NOE 실험에서는 강한 신호를 억제하여 매우 작은 NOE를 검출할 수 있는 과도 실험입니다.

핵과잉 사용자 효과의 예

핵오버하우저^[20] 효과

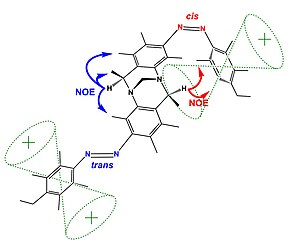
그림(위)은 핵과잉 사용자 효과 분광법이 전환 가능한 화합물의 구조를 어떻게 설명할 수 있는지를 보여준다.이 ^[20]예에서 {H}로 지정된 양성자는 전환 가능한 아조 그룹의 이성화 상태(cis 또는 trans)에 따라 두 세트의 NOE를 나타냅니다.트랜스 상태에서 양성자 {H}은 파란색 NOE를 나타내는 페닐기와는 거리가 멀고, 시스 상태는 페닐기 근처에서 양성자 {H}을 유지하여 새로운 NOE(빨간색 표시)의 출현을 초래한다.

또 다른 예(아래)에서는 NOE가 공진을 할당하고 구성을 결정하는 데 유용한 애플리케이션이 다당류입니다.예를 들어, 복합 글루칸은 특히 양성자 스펙트럼에서 다수의 중복 신호를 가지고 있다.따라서 신호 할당에는 NOESY를 포함한 2D NMR 실험을 활용하는 것이 유리합니다.예를 들어, 탄수화물의 NOE를 보세요.

탄수화물 연구의 동핵 NMR 기술.

「」를 참조해 주세요.

레퍼런스

^ Noggle, Joseph H.; Schirmer, Roger E. (1971). The Nuclear Overhauser Effect: Chemical Applications. Academic Press.
^ Neuhaus, David; Williamson, Michael P. (2000). The Nuclear Overhauser Effect in Structural and Conformational Analysis, 2nd ed. Wiley-VCH.
^ ^a ^b ^c ^d ^e ^f Claridge, Timothy D.W. (2016). High Resolution NMR Techniques in Organic Chemistry, 3rd ed. Elsevier. p. 315. ISBN 978-0080999869.
^ Kulhmann, Karl F.; Grant, David M.; Harris, Robin K. (1970). "Nuclear Overhauser Effects and ¹³C Relaxation Times in ¹³C {H} Double Resonance Spectra". Journal of Chemical Physics. 52 (7): 3439–3448. doi:10.1063/1.1673508.
^ Overhauser, Albert W. (1953). "Polarization of Nuclei in Metals". Physical Review. 92 (2): 411–5. doi:10.1103/PhysRev.92.411.
^ Carver, T.R.; Slichter, C.P. (1953). "Polarization of Nuclear Spins in Metals". Physical Review. 92 (1): 212–213. doi:10.1103/PhysRev.92.212.2.
^ Solomon, I (1955). "Relaxation Processes in a System of Two Spins" (PDF). Phys. Rev. 99 (2): 559. doi:10.1103/PhysRev.99.559.
^ Kaiser, R. (1962). "Use of the Nuclear Overhauser Effect in the Analysis of High‐Resolution Nuclear Magnetic Resonance Spectra". The Journal of Chemical Physics. 39 (1): 2435–2442. doi:10.1063/1.1734045.
^ ^a ^b Anet, F. A. L.; Bourn, A. J. R (1965). "Nuclear Magnetic Resonance Spectral Assignments from Nuclear Overhauser Effects". Journal of the American Chemical Society. 87 (22): 5250–5251. doi:10.1021/ja00950a048.
^ ^a ^b R.A., Bell; Saunders, J.K. (1970). "Correlation of the intramolecular nuclear Overhauser effect with internuclear distance". Can. J. Chem. 48 (7): 1114–1122. doi:10.1139/v70-184.
^ Schirmer, R.E.; Noggle, J.H.; Davis, J.P.; Hart, P.A. (1970). "Determination of molecular geometry by quantitative application of the nuclear Overhauser effect". J. Am. Chem. Soc. 92 (11): 3266–3273. doi:10.1021/ja00714a005.
^ "The Nobel Prize in Chemistry 1991". Nobelprize.org. Retrieved 2018-03-07.
^ "The Nobel Prize in Chemistry 2002". Nobelprize.org. Retrieved 2011-03-24.
^ Kumar, Anil; Ernst, R.R.; Wüthrich, K. (July 1980). "A two-dimensional nuclear Overhauser enhancement (2D NOE) experiment for the elucidation of complete proton-proton cross-relaxation networks in biological macromolecules". Biochemical and Biophysical Research Communications. 95 (1): 1–6. doi:10.1016/0006-291X(80)90695-6. PMID 7417242.
^ ^a ^b ^c Derome, Andrew E. (1987). Modern NMR Techniques for Chemistry Research. Pergamon. p. 106. ISBN 978-0080325149.
^ David E. Condon; Ilyas Yildirim; Scott D. Kennedy; Brendan C. Mort; Ryszard Kierzek; Douglas H. Turner (December 2013). "Optimization of an AMBER Force Field for the Artificial Nucleic Acid, LNA, and Benchmarking with NMR of L(CAAU)". J. Phys. Chem. B. 118 (5): 1216–1228. doi:10.1021/jp408909t. PMC 3917691. PMID 24377321.
^ Condon DE, Kennedy SD, Mort BC, Kierzek R, Yildirim I, Turner DH (June 2015). "Stacking in RNA: NMR of Four Tetramers Benchmark Molecular Dynamics". Journal of Chemical Theory and Computation. 11 (6): 2729–2742. doi:10.1021/ct501025q. PMC 4463549. PMID 26082675.
^ Braun, W.; Gō, N. (1985). "Calculation of Protein Conformations by Proton-Proton Distance Constraints A New Efficient Algorithm". J. Mol. Biol. 186 (3): 611–626. doi:10.1016/0022-2836(85)90134-2. PMID 2419572.
^ Ni, Feng; Scheraga, Harold A. (1994). "Use of the Transferred Nuclear Overhauser Effect To Determine the Conformations of Ligands Bound to Proteins". Accounts of Chemical Research. 27 (9): 257–264. doi:10.1021/ar00045a001. ISSN 0001-4842.
^ ^a ^b M. Kazem-Rostami, N. G. Akhmedov and S. Faramarzi (2019). "Molecular lambda shape light-driven dual switches: spectroscopic and computational studies of the photoisomerization of bisazo Tröger base analogs". Journal of Molecular Structure. 1178: 538–543. doi:10.1016/j.molstruc.2018.10.071.

외부 링크

[Noggle-1] Noggle, Joseph H.; Schirmer, Roger E. (1971). The Nuclear Overhauser Effect: Chemical Applications. Academic Press.

[Neuhaus-2] Neuhaus, David; Williamson, Michael P. (2000). The Nuclear Overhauser Effect in Structural and Conformational Analysis, 2nd ed. Wiley-VCH.

[Claridge-3] ^ ^a ^b ^c ^d ^e ^f Claridge, Timothy D.W. (2016). High Resolution NMR Techniques in Organic Chemistry, 3rd ed. Elsevier. p. 315. ISBN 978-0080999869.

[4] Kulhmann, Karl F.; Grant, David M.; Harris, Robin K. (1970). "Nuclear Overhauser Effects and ¹³C Relaxation Times in ¹³C {H} Double Resonance Spectra". Journal of Chemical Physics. 52 (7): 3439–3448. doi:10.1063/1.1673508.

[5] Overhauser, Albert W. (1953). "Polarization of Nuclei in Metals". Physical Review. 92 (2): 411–5. doi:10.1103/PhysRev.92.411.

[6] Carver, T.R.; Slichter, C.P. (1953). "Polarization of Nuclear Spins in Metals". Physical Review. 92 (1): 212–213. doi:10.1103/PhysRev.92.212.2.

[7] Solomon, I (1955). "Relaxation Processes in a System of Two Spins" (PDF). Phys. Rev. 99 (2): 559. doi:10.1103/PhysRev.99.559.

[8] Kaiser, R. (1962). "Use of the Nuclear Overhauser Effect in the Analysis of High‐Resolution Nuclear Magnetic Resonance Spectra". The Journal of Chemical Physics. 39 (1): 2435–2442. doi:10.1063/1.1734045.

[Anet-9] Anet, F. A. L.; Bourn, A. J. R (1965). "Nuclear Magnetic Resonance Spectral Assignments from Nuclear Overhauser Effects". Journal of the American Chemical Society. 87 (22): 5250–5251. doi:10.1021/ja00950a048.

[Bell-10] R.A., Bell; Saunders, J.K. (1970). "Correlation of the intramolecular nuclear Overhauser effect with internuclear distance". Can. J. Chem. 48 (7): 1114–1122. doi:10.1139/v70-184.

[11] Schirmer, R.E.; Noggle, J.H.; Davis, J.P.; Hart, P.A. (1970). "Determination of molecular geometry by quantitative application of the nuclear Overhauser effect". J. Am. Chem. Soc. 92 (11): 3266–3273. doi:10.1021/ja00714a005.

[12] "The Nobel Prize in Chemistry 1991". Nobelprize.org. Retrieved 2018-03-07.

[13] "The Nobel Prize in Chemistry 2002". Nobelprize.org. Retrieved 2011-03-24.

[14] Kumar, Anil; Ernst, R.R.; Wüthrich, K. (July 1980). "A two-dimensional nuclear Overhauser enhancement (2D NOE) experiment for the elucidation of complete proton-proton cross-relaxation networks in biological macromolecules". Biochemical and Biophysical Research Communications. 95 (1): 1–6. doi:10.1016/0006-291X(80)90695-6. PMID 7417242.

[Derome-15] Derome, Andrew E. (1987). Modern NMR Techniques for Chemistry Research. Pergamon. p. 106. ISBN 978-0080325149.

[16] David E. Condon; Ilyas Yildirim; Scott D. Kennedy; Brendan C. Mort; Ryszard Kierzek; Douglas H. Turner (December 2013). "Optimization of an AMBER Force Field for the Artificial Nucleic Acid, LNA, and Benchmarking with NMR of L(CAAU)". J. Phys. Chem. B. 118 (5): 1216–1228. doi:10.1021/jp408909t. PMC 3917691. PMID 24377321.

[Condon2015-17] Condon DE, Kennedy SD, Mort BC, Kierzek R, Yildirim I, Turner DH (June 2015). "Stacking in RNA: NMR of Four Tetramers Benchmark Molecular Dynamics". Journal of Chemical Theory and Computation. 11 (6): 2729–2742. doi:10.1021/ct501025q. PMC 4463549. PMID 26082675.

[18] Braun, W.; Gō, N. (1985). "Calculation of Protein Conformations by Proton-Proton Distance Constraints A New Efficient Algorithm". J. Mol. Biol. 186 (3): 611–626. doi:10.1016/0022-2836(85)90134-2. PMID 2419572.

[NiScheraga1994-19] Ni, Feng; Scheraga, Harold A. (1994). "Use of the Transferred Nuclear Overhauser Effect To Determine the Conformations of Ligands Bound to Proteins". Accounts of Chemical Research. 27 (9): 257–264. doi:10.1021/ar00045a001. ISSN 0001-4842.

[:0-20] M. Kazem-Rostami, N. G. Akhmedov and S. Faramarzi (2019). "Molecular lambda shape light-driven dual switches: spectroscopic and computational studies of the photoisomerization of bisazo Tröger base analogs". Journal of Molecular Structure. 1178: 538–543. doi:10.1016/j.molstruc.2018.10.071.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[11]

[12]

[13]

[14]

[15]

[10]

[16]

[17]

[18]

[19]

[20]

Search

핵오버하우저 효과

네임스페이스

더

목차

역사

릴렉스

분자 운동

구조 설명

2차원 NMR

이종핵 NOE

몇 가지 실험 방법

핵과잉 사용자 효과의 예

「」를 참조해 주세요.

레퍼런스

외부 링크

Search

핵오버하우저 효과

역사

릴렉스

분자 운동

구조 설명

2차원 NMR

이종핵 NOE

몇 가지 실험 방법

핵과잉 사용자 효과의 예

「 」를 참조해 주세요.

레퍼런스

외부 링크

「」를 참조해 주세요.