병렬 외장 메모리

PEM 모델

컴퓨터 과학에서 PEM(Parallel External Memory) 모델은 캐시 인식 외부 메모리 추상 머신입니다.^[1]이것은 싱글 프로세서 외장 메모리(EM) 모델과 병렬 컴퓨팅의 유사점입니다.마찬가지로 Parallel Random-Access Machine(PRAM; 병렬랜덤액세스 머신)에 대한 캐시 인식 유추입니다.PEM 모델은 다수의 프로세서와 각각의 개인 캐시 및 공유 메인메모리로 구성됩니다.

모델

정의.

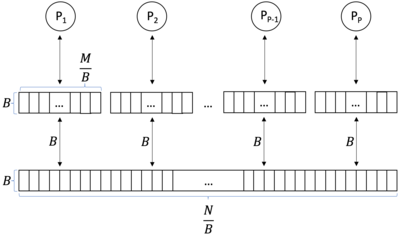
PEM 모델은^[1] EM 모델과 PRAM 모델의 조합입니다.PEM 모델은 P $\displaystyle$ P 프로세서와 $P$ 2레벨 메모리 계층으로 구성된 $계산$ 모델입니다.이 메모리 계층은 $크기$ N({ $displaystyle$ N})과 $N$ P({ $displaystyle$ P})의 $P$ 작은 내장 메모리(캐시)로 구성됩니다.CPU는 메인 메모리를 공유합니다.각 캐시는 1개의 프로세서 전용입니다.프로세서는 다른 프로세서의 캐시에 액세스할 수 없습니다.캐시의 $M$ 는 M $(\displaystyle$ M $)$ 으로 $M$ , 사이즈 $B$ (\ $displaystyle$ B $B$ 의 블록으로 분할되어 있습니다.프로세서는 캐시에 있는 데이터에 대해서만 작업을 수행할 수 있습니다.데이터는 메인 메모리와 캐시 간에 $크기$ B(\ $displaystyle$ B $B$ 블록으로 전송할 수 있습니다.

I/O의 복잡성

PEM 모델의 복잡도 척도는 메인 메모리와 ^[1]캐시 간의 병렬 블록 전송 수를 결정하는 I/O 복잡도입니다.병렬 블록 전송 중에는 각 프로세서가 블록을 전송할 수 있습니다.따라서 P $(\displaystyle$ $O(P)$ P $O(P)$ 프로세서가 $P$ 메인 메모리를 형성하는 B $(\$ $displaystyle$ B $)$ $B$ 의 $B$ 데이터 블록을 캐시에 병렬로 로드하는 $경우$ , 이는 O $P)$ 가 $O(P)$ O $(1)$ 의 $O(1)$ I/O 복잡도로 간주됩니다 $.$ PEM 모델 간의 $메인 데이터$ 전송을 최소화해야 합니다.캐시 내의 데이터를 가능한 한 많이 캐시하여 동작시킵니다.

읽기/쓰기 충돌

PEM 모델에서는, P프로세서간에 직접 통신 네트워크는 없습니다.프로세서는 메인 메모리를 통해 간접적으로 통신해야 합니다.복수의 프로세서가 메인 메모리내의 같은 블록에 액세스 하려고 하면, 동시에 읽기/쓰기^[1] 경합이 발생합니다.PRAM 모델과 마찬가지로 이 문제의 3가지 다른 변형이 고려됩니다.

동시 읽기 동시 쓰기(CRCW):메인 메모리의 같은 블록은, 복수의 프로세서로 동시에 읽고 쓸 수 있습니다.
동시 읽기 전용 쓰기(CREW):메인 메모리의 같은 블록을 복수의 프로세서로 동시에 읽어낼 수 있습니다.블록에 쓸 수 있는 프로세서는 한 번에 1개뿐입니다.
전용 읽기 전용 쓰기(EREW):메인 메모리의 같은 블록은, 복수의 프로세서로 동시에 읽거나 쓸 수 없습니다.한 번에 한 블록에 액세스할 수 있는 프로세서는 1개뿐입니다.

$다음$ 2개의^[1] 알고리즘은 P $P\leq B$ B(\ $displaystyle$ P\leq B $)$ 프로세서가 $P\leq B$ 같은 블록에 동시에 쓸 $P\leq B$ CREW 및 EREW 문제를 해결합니다.첫 번째 방법은 쓰기 작업을 직렬화하는 것입니다.블록에 기입하는 프로세서는 1개뿐입니다.그 결과 총 P $\style$ P $\display$ P\parallel $P$ block 전송이 $이루어집니다$ .두 번째 접근법에서는 O $O(\log(P))$ ( $O(\log(P))$ $O(\log(P))$ ( $O(\log(P))$ ) $O(\log(P))$ \ $displaystyle$ O ( \ $log$ ( $P$ ) } )패럴렐 $O(\log(P))$ 블록 전송과 각 프로세서에 대한 추가 블록이 $O(\log(P))$ 합니다.주요 아이디어는 쓰기 작업을 바이너리 트리 방식으로 예약하고 데이터를 점차 단일 블록으로 결합하는 것입니다.첫 번째 $P$ 에서P{ $displaystyle$ P $}$ 프로세서는 $P$ $블록$ 을 P/2{ $P/2$ P/2} $블록$ 으로 $P/2$ 합니다. $P/2$ 다음 $P/2$ /2 $(디스플레이 스타일$ P/2 $)$ 프로세서는 $P/2$ $P/2$ P/ $(디스플레이 스타일$ P/ $2)$ $P/2$ 을 $P/2$ $P/4$ P/4 $(디스플레이 스타일$ P/ $4$ 로 결합합니다. 이 절차는 모든 데이터가 하나의 블록에 결합될 때까지 계속됩니다.

다른 모델과의 비교


모델	멀티코어	캐시 인식
랜덤 액세스 머신(RAM)	아니요.	아니요.
Parallel Random-Access Machine(PRAM; 병렬 랜덤 액세스 머신)	네.	아니요.
외장 메모리(EM)	아니요.	네.
병렬 외장 메모리(PEM)	네.	네.

예

멀티웨이 파티션

$M=\{m_{1},...,m_{d-1}\}$ $M=\{m_{1},...,m_{d-1}\}$ { $M=\{m_{1},...,m_{d-1}\}$ , $M=\{m_{1},...,m_{d-1}\}$ . $M=\{m_{1},...,m_{d-1}\}$ . , $M=\{m_{1},...,m_{d-1}\}$ m $M=\{m_{1},...,m_{d-1}\}$ - 1 $}$ { $displaystyle$ M = \ { m $_$ { $1$ , ... m $_$ { d - 1 $M=\{m_{1},...,m_{d-1}\}$ } } a- $M=\{m_{1},...,m_{d-1}\}$ d-1 피벗의 벡터라고 합니다.A $(\displaystyle$ A $)$ 를 $A$ N개 요소의 순서없는 세트라고 $합니다$ . $A의$ d웨이^[1] 파티션은 세트 $\Pi =\{A_{1},...,A_{d}\}$ $\Pi =\{A_{1},...,A_{d}\}$ { $\Pi =\{A_{1},...,A_{d}\}$ 1 $\Pi =\{A_{1},...,A_{d}\}$ , $\Pi =\{A_{1},...,A_{d}\}$ . $\Pi =\{A_{1},...,A_{d}\}$ , $\Pi =\{A_{1},...,A_{d}\}$ d $}$ { $displaystyle$ \ $Pi$ = \ { A $_$ {1 $}$ 。 $A_{d}\}.$ 여기서 $\cup _{i=1}^{d}A_{i}=A$ i $\cup _{i=1}^{d}A_{i}=A$ $\cup _{i=1}^{d}A_{i}=A$ $\cup _{i=1}^{d}A_{i}=A$ $\cup _{i=1}^{d}A_{i}=A$ $\cup _{i=1}^{d}A_{i}=A$ \ $displaystyle$ \ $cup$ _ { i $\cup _{i=1}^{d}A_{i}=A$ = $1$ }^{ $d$ } $A_{i}=A}$ $A_{i}\cap A_{j}=\emptyset$ $A_{i}\cap A_{j}=\emptyset$ $A_{i}\cap A_{j}=\emptyset$ a A $1\leq i<j\leq d$ A j $A_{i}\cap A_{j}=\emptyset$ = \ $displaystyle$ A_ ${i}$ \ $cap$ A_ ${j$ $}$ = \ $emptyset$ } ( $1\leq i<j\leq d$ $1\leq i<j\leq d$ i $1\leq i<j\leq d$ i $）$ 。 $A_{i}$ \ $displaystyle$ 1 \ $leq$ $A_{i}$ $i$ $A_{i}$ $1\leq i<j\leq d$ 。구성 요소들의 나는{\displaystyle A_{나는}}는 것보다 m나는 − 1{\displaystyle m_{i-1}}와 m나는 2{\displaystyle m_{나는}^{2}보다} 작아진다. 다음에 algorithm[1]입력 N/P-sized 인접해 세그먼트 S1,으로 나눠져 있다. 큰 경우, SP{\displaystyle S_{1},...,S_{P}}mai에서 수입니다.n메모리. 프로세서i는 주로 $S_{i}$ i $(\$ 에서 동작합니다.멀티웨이 파티션알고리즘(PEM_DIST_SORT^[1])는 PEM 프리픽스 합계^[1] 알고리즘을 사용하여 $O\left({\frac {N}{PB}}+\log(P)\right)$ 의 $O\left({\frac {N}{PB}}+\log(P)\right)$ O ( $O\left({\frac {N}{PB}}+\log(P)\right)$ P $O\left({\frac {N}{PB}}+\log(P)\right)$ + log ) $O\left({\frac {N}{PB}}+\log(P)\right)$ ( $O\left({\frac {N}{PB}}+\log(P)\right)$ ) $O\left({\frac {N}{PB}}+\log(P)\right)$ \ $displaystyle O$ \ left ( { \ $frac$ { $O\left({\frac {N}{PB}}+\log(P)\right)$ N $O\left({\frac {N}{PB}}+\log(P)\right)$ } { $PB$ } + \ $log$ ( $P$ ) \ $right$ } I $O\left({\frac {N}{PB}}+\log(P)\right)$ /O 복잡도를 가진 프리픽스 합계를 계산합니다.이 알고리즘은 최적의 PRAM 프리픽스 합계 알고리즘을 시뮬레이트합니다.

// 각 프로세서 i에 대해 데이터  $S_{i}$   $S_{i}$ {\ $displaystyle S_{$ i $S_{i}$ }의 d-way 파티션을 병렬로 계산하여 M {\ $display$ M}을 $($ 를 $M$  $)$  캐시에 피벗하는 벡터를 읽습니다. $(\$ })를 $S_{i}$  d버킷으로  $S_{i}$ 하고  $M_{i}=\{j_{1}^{i},...,j_{d}^{i}\}$   $M_{i}=\{j_{1}^{i},...,j_{d}^{i}\}$   $=$  {  $M_{i}=\{j_{1}^{i},...,j_{d}^{i}\}$   $M_{i}=\{j_{1}^{i},...,j_{d}^{i}\}$ i $M_{i}=\{j_{1}^{i},...,j_{d}^{i}\}$ , $M_{i}=\{j_{1}^{i},...,j_{d}^{i}\}$ . ,  $M_{i}=\{j_{1}^{i},...,j_{d}^{i}\}$   $M_{i}=\{j_{1}^{i},...,j_{d}^{i}\}$ }({i}=\{ $j_{1}^{i},$  ... $j_{d}^{i}\})$ 를 $M_{i}=\{j_{1}^{i},...,j_{d}^{i}\}$  각 버킷의 항목 수로 합니다.end $\{M_{1},...,M_{P}\}$   $\{M_{1},...,M_{P}\}$ { M $\{M_{1},...,M_{P}\}$ 1 $\{M_{1},...,M_{P}\}$ , . ,  $\{M_{1},...,M_{P}\}$  P $}$  ({  $displaystyle$  $\{M_{1},...,M_{P}\}$ \ { $M$  _ {1} ,  $...$  ,  $M$  _ {  $P$  $\{M_{1},...,M_{P}\}$  $}$  )세트로 $\{M_{1},...,M_{P}\}$  $S_{i}$  PEM 프리픽스 합계를 동시에 실행합니다.// 프리픽스 합 벡터를 사용하여  $S_{i}$  프로세서i의  $S_{i}$  파티션을 오프셋 M  $M_{i-1}$ 에 병렬로 씁니다 $.$  $M_{i-1}$ -  $({$ M_{ $i-1})$  및 $M_{i-1}$   $({$   $({$ displaystyle  $M_{P})$ 에 $M_P$  저장된 프리픽스 합계를 사용하는 경우 마지막 프로세서 P는 버킷  $B$ 의벡터 B({ $displaystyle$ B})를 $B$  계산하여 반환합니다 $M_{i-1}$

만약 d의 벡터)O형이며 입력한 연속적인 메모리에 위치한다, 다음 d-way 분할 문제는 개별 공조 시스템 모델에 O형인(NPB+⌈ dB⌉<>를 사용하여 로그 ⁡(P)+d로그 ⁡(B)){\displaystyle O\left({\frac{N}{PB}}+\left\lc 해결될 수 있{\displaystyle d=O\left({\frac{M}{B}}\right)}피벗 M(MB).eil $\frac {d}$ { $B}$ \ right \ $rceil$ > \ $log$ ( $P$ ) + $d$ \ $log$ ( $B$ ) \ $right$ } I $O\left({\frac {N}{PB}}+\left\lceil {\frac {d}{B}}\right\rceil >\log(P)+d\log(B)\right)$ /O의 복잡성.마지막 버킷의 내용은 연속된 메모리에 위치해야 합니다.

선택.

$({displaystyle$ N $A$ $N$ $A$ 입니다.다음^[1] 코드는 다음을 사용합니다.PRAMSORT이 알고리즘은 O $O(\log N)$ N $)\displaystyle$ O $(\log$ N $O(\log N)$ 에서 실행되는 PRAM 최적 정렬 알고리즘입니다.SELECT캐시 최적 단일 패킷 선택 알고리즘입니다.

N이 $(\displaystyle$  N $\leq$  P $)$ 이면 $N\leq P$   $($   $)$  {\ $displaystyle$  { $PRAMSORT}(A,P)}$ 는 ${\texttt {PRAMSORT}}(A,P)$  $S_{i}$  A $[$  $](\$  $displaystyle$  A $[k$  $])$ 를 $A[k]$  $i$  반환한다 $.$  $isplaystyle m_{i}=syslogtextt {SELECT}(S_{i},{\frac {N}{2P}})$ 의 $m_{i}={\texttt {SELECT}}(S_{i},{\frac {N}{2P}})$  경우 //  ${\texttt {PRAMSORT}}(\lbrace m_{1},\dots ,m_{2}\rbrace ,P)$ PRAMSORT $({$ 1,  ${\texttt {PRAMSORT}}(\lbrace m_{1},\dots ,m_{2}\rbrace ,P)$   $},$   $)\displaystyle$ {\ $textt m_1},\brace_{2}$ 의 종료 $}}(A,m_{P/2$ }, $k\leq t$  $)$  $k\leq t$ k $t={\texttt {PEMPARTITION}}(A,m_{P/2},P)$  $k\leq t$ t  $t$  { $displaystyle k\leq$ t}이면 $k\leq t$   ${\texttt {PEMSELECT}}(A[1:t],P,k)$   ${\texttt {PEMSELECT}}(A[1:t],P,k)$ [ 1 ${\texttt {PEMSELECT}}(A[1:t],P,k)$ :  ${\texttt {PEMSELECT}}(A[1:t],P,k)$ ] ,  ${\texttt {PEMSELECT}}(A[1:t],P,k)$ , k  $)$  { $displaystyle$  {  $PEM SELECT$ }( $A$ [ 1 :  $t$ ] , $P$  , ${\texttt {PEMSELECT}}(A[1:t],P,k)$ k )를 ${\texttt {PEMSELECT}}(A[1:t],P,k)$  반환하고, 그렇지 않으면  ${\texttt {PEMSELECT}}(A[t+1:N],P,k-t)$ 은 1 ${\texttt {PEMSELECT}}(A[t+1:N],P,k-t)$ + $1$ 을 ${\texttt {PEMSELECT}}(A[t+1:N],P,k-t)$   ${\texttt {PEMSELECT}}(A[t+1:N],P,k-t)$ 합니다 ${\texttt {PEMSELECT}}(A[t+1:N],P,k-t)$

입력이 연속 메모리에 저장되어 있다고 가정하면PEMSELECT의 I/O 복잡도는 다음과 같습니다.

$({\frac {N}{PB}}+\log(PB)\cdot \log({\frac {N}{P}})})$

배포 정렬

배포 정렬은 $입력$ $목록$ A $(\$ $displaystyle$ N $)$ 를 $A$ $N$ 유사한 크기의 d $(\displaystyle$ d $)$ 개의 $d$ 분리된 버킷으로 $d$ 합니다.그런 다음 모든 버킷이 재귀적으로 정렬되고 결과가 완전히 정렬된 목록으로 결합됩니다.

P $P=1$ { $displaystyle$ P $=1}$ 인 $P=1$ 경우 작업은 캐시 최적 단일 정렬 알고리즘에 위임됩니다.

그 이외의 경우는, 다음의^[1] 알고리즘이 사용됩니다.

나는 병렬로{\displaystyle 나는}각 프로세서에 대한{A\displaystyle}에서 끓여샘플 4Nd{\displaystyle{\tfrac{4N}{\sqrt{d}}}}부분을 만약 M<>S나는{\displaystyle M<, S_{나는}}그때 d)M/B{\displaystyle d=M/B}부하 S나는{\displaystyle S_{나는}}에 M.  {\dis $Playstyle$  M $}$  - size $M$  page and sort page into  $d=|S_{i}|$  d $= S_$  ${i}$   $S_{i}$ 를 $d=|S_{i}|$  로드하고  $S_{i}$ 합니다 ${\sqrt {d}}/4$  정렬된 메모리의 d / 4 {  $displaystyle {d}$  / $4$  '번째 요소를 연속된  $R^{i}$  { $i$  $}$ 로 $S_{i}$  선택합니다(\ $displaystyle$  di} ） 。샘플의  $splaystyle R^{i$ }가 병렬로 종료되는 경우  $R^{1}\dots R^{P}$   $R^{1}\dots R^{P}$ …  $R^{1}\dots R^{P}$ {\ $displaystyle$  R $^{1$ }\ $dots$ R^{P $R^{1}\dots R^{P}$  $}$ 을(를) 단일 연속  ${\mathcal {R}}$ R  ${\$  $displaystyle$  ${\mathcal {R}}$ {\ $mathcal$  { ${\mathcal {R}}_{1}\dots {\mathcal {R}}_{\sqrt {d}}$ 로 ${\mathcal {R}}$  ${\sqrt {d}}$   ${\mathcal {R}}_{1}\dots {\mathcal {R}}_{\sqrt {d}}$ 한다 $.$  $\displaystyle {\displaystyle$  { $R}$ _ ${\sqrt$  {d $}}$  끝 ${\mathcal {R}}_{1}\dots {\mathcal {R}}_{\sqrt {d}}$  do $//\$  {\ $d$  $}$ 을 ${\sqrt {d}}$  ${\mathcal {M}}[j]$ 를) 찾습니다 $.\$ displaystyle { $M}[$ j ${\mathcal {M}}[j]$  $]$ 는 j  $j=1$   $j=1$ {\ $displaystyle$  j $=1$ }에서 $j=1$  ${\sqrt {d}}$  {d $}($ 으 ${\sqrt {d}}$ )로  $회전합니다.$  $j$   ${\mathcal {M}}[j]={\texttt {PEMSELECT}}({\mathcal {R}}_{i},{\tfrac {P}{\sqrt {d}}},{\tfrac {j\cdot 4N}{d}})$   ${\mathcal {M}}[j]={\texttt {PEMSELECT}}({\mathcal {R}}_{i},{\tfrac {P}{\sqrt {d}}},{\tfrac {j\cdot 4N}{d}})$   ${\mathcal {M}}[j]={\texttt {PEMSELECT}}({\mathcal {R}}_{i},{\tfrac {P}{\sqrt {d}}},{\tfrac {j\cdot 4N}{d}})$  ) ${\mathcal {M}}[j]={\texttt {PEMSELECT}}({\mathcal {R}}_{i},{\tfrac {P}{\sqrt {d}}},{\tfrac {j\cdot 4N}{d}})$ {\ $style$  ${mathcal$  { $M}}[j]= pemselecttextt$ {PEMSELECT $}({\mathcal$  { $R}_i},$  {\ $tfrac$  {P $}{\sqrt {$ d}}}),  ${\tfrac {$ j $\cdot 4N$  $}}}}}}}:$  인접한  $어레이$ 의 피벗의 엔드 팩 ${\mathcal {M}}[j]={\texttt {PEMSELECT}}({\mathcal {R}}_{i},{\tfrac {P}{\sqrt {d}}},{\tfrac {j\cdot 4N}{d}})$  ${\mathcal {B}}={\texttt {PEMMULTIPARTITION}}(A[1:N],{\mathcal {M}},{\sqrt {d}},P)$   ${\mathcal {B}}={\texttt {PEMMULTIPARTITION}}(A[1:N],{\mathcal {M}},{\sqrt {d}},P)$   ${\mathcal {B}}={\texttt {PEMMULTIPARTITION}}(A[1:N],{\mathcal {M}},{\sqrt {d}},P)$ ( ${\mathcal {B}}={\texttt {PEMMULTIPARTITION}}(A[1:N],{\mathcal {M}},{\sqrt {d}},P)$  [  ${\mathcal {B}}={\texttt {PEMMULTIPARTITION}}(A[1:N],{\mathcal {M}},{\sqrt {d}},P)$ :  ${\mathcal {B}}={\texttt {PEMMULTIPARTITION}}(A[1:N],{\mathcal {M}},{\sqrt {d}},P)$  , ${\mathcal {B}}={\texttt {PEMMULTIPARTITION}}(A[1:N],{\mathcal {M}},{\sqrt {d}},P)$  , ${\mathcal {B}}={\texttt {PEMMULTIPARTITION}}(A[1:N],{\mathcal {M}},{\sqrt {d}},P)$  , ${\mathcal {B}}={\texttt {PEMMULTIPARTITION}}(A[1:N],{\mathcal {M}},{\sqrt {d}},P)$ ) {  $displaystyle$ { $mathcal$ { B}} = $texttt$ {  $PEMMULTIPARTION}$  （  $A$ [  $1$ :  $N$ ] , { \  $mathcal$ {  $M$ } , { \  $sqrt }$   ${\mathcal {B}}={\texttt {PEMMULTIPARTITION}}(A[1:N],{\mathcal {M}},{\sqrt {d}},P)$ } ${\mathcal {B}}={\texttt {PEMMULTIPARTITION}}(A[1:N],{\mathcal {M}},{\sqrt {d}},P)$ ） sort 、 、 sort  $buckets$  sort 。 $O$  $O\left(\left\lceil {\tfrac {{\mathcal {B}}[j]}{N/P}}\right\rceil \right)$ ( $O\left(\left\lceil {\tfrac {{\mathcal {B}}[j]}{N/P}}\right\rceil \right)$ B [ $O\left(\left\lceil {\tfrac {{\mathcal {B}}[j]}{N/P}}\right\rceil \right)$  ] $O\left(\left\lceil {\tfrac {{\mathcal {B}}[j]}{N/P}}\right\rceil \right)$  / P  $O\left(\left\lceil {\tfrac {{\mathcal {B}}[j]}{N/P}}\right\rceil \right)$  ) $O\left(\left\lceil {\tfrac {{\mathcal {B}}[j]}{N/P}}\right\rceil \right)$ ( \  $displaystyle O$  \  $left$  $O\left(\left\lceil {\tfrac {{\mathcal {B}}[j]}{N/P}}\right\rceil \right)$ ( \ $left$  \  $lceil$ { \  $frac$ { \  $mathcal$ {  $B$  $}$  )를 ${\mathcal {B}}[j]$   $O\left(\left\lceil {\tfrac {{\mathcal {B}}[j]}{N/P}}\right\rceil \right)$ 하여 ${\texttt {PEMDISTSORT}}$ B ${\mathcal {B}}[j]$ [ ${\mathcal {B}}[j]$  $O\left(\left\lceil {\tfrac {{\mathcal {B}}[j]}{N/P}}\right\rceil \right)$  $]$ 의  $버킷$  j {\  $displaystyle {$ PEMDISTSORT ${\texttt {PEMDISTSORT}}$ }}를 ${\texttt {PEMDISTSORT}}$  $j$  lay 합니다 $.$  $버킷$  $j의$ 요소를 담당하는  ${N/$ P}\ $right$ \rceil $\right}$  프로세서 $O\left(\left\lceil {\tfrac {{\mathcal {B}}[j]}{N/P}}\right\rceil \right)$  $j$  $O\left(\left\lceil {\tfrac {{\mathcal {B}}[j]}{N/P}}\right\rceil \right)$ 끝 $:$

I/O의 복잡성PEMDISTSORT다음과 같습니다.

$(\displaystyle O\left(\left\lceil {PB})\rceil \left(\log _{d}P+\log _{M/B}{PB}}\right)+f(N,P,d)\cdot \{dP}\right}\right)$

어디에

$(\displaystyle f(N,P,d)=O\left(\log {PB}{sqrt {d}})\log {frac {N}{P}}+\left\lceil {frac {d}}\log P+{\sqrt {d}\lcrt {d}\lce)\left(오른쪽)$

프로세서의 수가 $f(N,P,d)=O\left(\left\lceil {\tfrac {N}{PB}}\right\rceil \right)$ $f(N,P,d)=O\left(\left\lceil {\tfrac {N}{PB}}\right\rceil \right)$ d) $f(N,P,d)=O\left(\left\lceil {\tfrac {N}{PB}}\right\rceil \right)$ O( $f(N,P,d)=O\left(\left\lceil {\tfrac {N}{PB}}\right\rceil \right)$ $f(N,P,d)=O\left(\left\lceil {\tfrac {N}{PB}}\right\rceil \right)$ P B $f(N,P,d)=O\left(\left\lceil {\tfrac {N}{PB}}\right\rceil \right)$ display $)(\$ f $(N, P,$ d) = $O\left(\left\lceil {PB})$ $M<B^{O(1)}$ $M$ $M<B^{O(1)}$ < $M<B^{O(1)}$ $f(N,P,d)=O\left(\left\lceil {\tfrac {N}{PB}}\right\rceil \right)$ \ $display$ 1 $($ $))$ 로 $f(N,P,d)=O\left(\left\lceil {\tfrac {N}{PB}}\right\rceil \right)$ 선택되었을 경우

$O\left({\frac {N}{PB}}\log _{M/B}{\frac {N}{B}}\right)$

기타 PEM 알고리즘


PEM 알고리즘	I/O의 복잡성	제약
머지소트^[1]	$O\left({\frac {N}{PB}}\log_{\frac {M}{B}}{\right}=textrm {sort}_{P}(N)$	$P\leq {N} {B^{2}}, M=B^{O(1)}$
리스트 랭킹^[2]	$O\left({\textrm {sort}}_{P}(N)\right)$	$P\leq {N/B^{2}}{\log B\cdot \log ^{O(1)}N}}, M=B^{O(1)}$
오일러 투어^[2]	$O\left({\textrm {sort}}_{P}(N)\right)$	$P\leq {N} {B^{2}}, M=B^{O(1)}$
식목^[2] 평가	$O\left({\textrm {sort}}_{P}(N)\right)$	$P\leq {B^{2}\log B\cdot \log ^{O(1)}N}, M=B^{O(1)}$
MST^[2] 검색	$\displaystyle O\left({\textrm {sort}_{P}(V)+{\textrm {sort}_{P}(E)\log {tfrac {V}{pB}}}\right})$	$p\leq {V + E }{B^{2}\log B\cdot \log ^{O(1)}N}}, M=B^{O(1)}}$

${\textrm {sort}}_{P}(N)$ 서 sort ${\textrm {sort}}_{P}(N)$ P ( ${\textrm {sort}}_{P}(N)$ ) ${\textrm {sort}}_{P}(N)$ { $style$ \ $textrm { sort$ } $_$ { $P$ } （ $N$ ）는 PEM ${\textrm {sort}}_{P}(N)$ 모델에서P { $display style$ P}프로세서를 $N$ $P$ $P$ 하여N개의 항목을 $N$ 하는 데 걸리는 시간입니다.

「」를 참조해 주세요.

Parallel Random-Access Machine(PRAM; 병렬 랜덤 액세스 머신)
랜덤 액세스 머신(RAM)
외장 메모리(EM)

레퍼런스

^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ^k ^l Arge, Lars; Goodrich, Michael T.; Nelson, Michael; Sitchinava, Nodari (2008). "Fundamental parallel algorithms for private-cache chip multiprocessors". Proceedings of the Twentieth Annual Symposium on Parallelism in Algorithms and Architectures - SPAA '08. New York, New York, USA: ACM Press: 197. doi:10.1145/1378533.1378573. ISBN 9781595939739.
^ ^a ^b ^c ^d Arge, Lars; Goodrich, Michael T.; Sitchinava, Nodari (2010). "Parallel external memory graph algorithms". 2010 IEEE International Symposium on Parallel & Distributed Processing (IPDPS). IEEE: 1–11. doi:10.1109/ipdps.2010.5470440. ISBN 9781424464425.

[:0-1] ^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ^k ^l Arge, Lars; Goodrich, Michael T.; Nelson, Michael; Sitchinava, Nodari (2008). "Fundamental parallel algorithms for private-cache chip multiprocessors". Proceedings of the Twentieth Annual Symposium on Parallelism in Algorithms and Architectures - SPAA '08. New York, New York, USA: ACM Press: 197. doi:10.1145/1378533.1378573. ISBN 9781595939739.

[:1-2] Arge, Lars; Goodrich, Michael T.; Sitchinava, Nodari (2010). "Parallel external memory graph algorithms". 2010 IEEE International Symposium on Parallel & Distributed Processing (IPDPS). IEEE: 1–11. doi:10.1109/ipdps.2010.5470440. ISBN 9781424464425.

[1]

[2]

v t 병렬 컴퓨팅
일반	분산 컴퓨팅 병렬 컴퓨팅 대규모 병렬화 클라우드 컴퓨팅 하이 퍼포먼스 멀티프로세서 멀티코어 프로세서 GPGPU 컴퓨터 네트워크 수축기 어레이
레벨	조금 설명 실 작업 데이터. 기억 고리 파이프라인
멀티스레딩	일시적 동시(SMT) 투기적(SpMT) 프리엠프티브 협동조합 클러스터화 멀티스레드(CMT) 하드웨어 스카우트
이론.	PRAM 모델 PEM 모델 병렬 알고리즘 분석 암달의 법칙 구스타프슨의 법칙 비용 효율 카르프-플랫 미터법 속도를 줄이세요. 스피드업
요소들	과정 실 파이버전 명령 창 어레이 데이터 구조
코디네이션	멀티프로세서 메모리 일관성 캐시 일관성 캐시 무효화 장벽 동기 응용 프로그램 체크 포인트
프로그래밍	스트림 처리 데이터 흐름 프로그래밍 모델 암묵적 병렬화 명시적 병렬화 동시성 논블로킹 알고리즘
하드웨어	플린의 분류법 SISD SIMD 어레이 처리(SIMT) 파이프라인 처리 연관 처리 미스테리 MIMD 데이터 흐름 아키텍처 파이프라인 프로세서 슈퍼스칼라 프로세서 벡터 프로세서 멀티프로세서 대칭의 비대칭의 기억 공유했습니다. 분산된 분산 공유 UMA NUMA 혼수 상태 대규모 병렬 컴퓨터 컴퓨터 클러스터 그리드 컴퓨터 하드웨어 액셀러레이션
API	아테지 PX 부스트 예배당 HPX Charm++ 칠크 코어레이 포트란 쿠다 드라이어드 C++ AMP 글로벌 어레이 GPUO펜 MPI OpenMP OpenCL OpenHMPP 오픈 ACC 병렬 확장 PVM 스레드 뗏목 립 ROCM UPC TBB ZPL
문제	자동 병렬화 교착 상태 결정론적 알고리즘 민망할 정도로 평행하다 병렬 속도 저하 레이스 조건 소프트웨어 록아웃 확장성 기아
카테고리: 병렬 컴퓨팅

Search

병렬 외장 메모리

네임스페이스

더

목차

모델

정의.

I/O의 복잡성

읽기/쓰기 충돌

다른 모델과의 비교

예

멀티웨이 파티션

선택.

배포 정렬

기타 PEM 알고리즘

「」를 참조해 주세요.

레퍼런스

Search

병렬 외장 메모리

모델

정의.

I/O의 복잡성

읽기/쓰기 충돌

다른 모델과의 비교

예

멀티웨이 파티션

선택.

배포 정렬

기타 PEM 알고리즘

「 」를 참조해 주세요.

레퍼런스

「」를 참조해 주세요.