직접 수량-영점 변환

다이렉트 쿼터 제로(DQZ 또는 DQ0^[1] 또는 DQO,^[2] 때로는 소문자) 변환 또는 제로 다이렉트^[3] 쿼터(0DQ 또는 ODQ, 때로는 소문자) 변환은 분석을 단순화하기 위한 노력으로 3원소 벡터 또는 3원소 매트릭스의 기준 프레임을 회전시키는 텐서다. DQZ 변환은 1929년 로버트 H. 박이 처음 제안한 클라크 변환과 파크 변환의 산물이다.^[4]

DQZ 변환은 흔히 3상 회로와 함께 전기 공학의 맥락에서 사용된다. 변환을 사용하여 AC 파형의 기준 프레임을 DC 신호가 되도록 회전시킬 수 있다. 그런 다음 실제 3상 AC 결과를 복구하기 위해 역변환을 수행하기 전에 이러한 DC 양에 대해 단순화된 계산을 수행할 수 있다. 예를 들어, DQZ 변환은 3상 동기식 기계에 대한 분석을 단순화하거나 3상 인버터의 제어를 위한 계산을 단순화하기 위해 자주 사용된다. 3상 동기식 기계의 분석에서 변환은 3상 스테이터와 로터 수량을 단일 회전 기준 프레임으로 전달하여 시간 변화 인덕턴스의 효과를 없애고 시스템을 선형 시간 변화 시스템으로 변환한다.

소개

DQZ 변환은 Park와 Clarke 변환 매트릭스로 만들어진다. 클라크 변환(Edith Clarke의 이름을 따서 명명)은 ABC 기준 프레임의 벡터를 αβ³의 기준 프레임으로 변환한다. 클라크 변환의 1차 값은 벡터의 세 가지 요소 모두에 공통적인 ABC 기준 벡터의 그 부분을 분리하는 것이다; 그것은 공통 모드 요소(즉, Z 구성요소)를 분리한다. 파워 인바리어스, 오른손잡이, 균일하게 크기가 조정된 클라크 변환 매트릭스는

KC=23⋅[1− 12− 12032− 32121212]{\displaystyle K_{C}={\sqrt{\frac{2}{3}}}\cdot{\begin{bmatrix}1&, -{\frac{1}{2}}&-{\frac{1}{2}}\\0&,{\frac{\sqrt{3}}{2}}&-{\frac{\sqrt{3}}{2}}\\{\frac{1}{\sqrt{2}}}&{\frac{1}{\sqrt{2}}}&a.융점.{\frac{1}{\sqrt${2}}:}\end{bmatrix$

ABC 기준 열 벡터를 XYZ 기준 프레임으로 변환하려면, 벡터를 Clarke 변환 매트릭스로 미리 곱해야 한다.

${\$$YZ}=K_{C}\cdot {\vec{u}}_{{{}}$$ABC$

그리고 XYZ 기준 열 벡터에서 ABC 기준 프레임으로 다시 변환하려면 역 Clarke 변환 매트릭스로 벡터를 미리 곱해야 한다.

${\$$ABC}=K_{C}^{-1}\cdot {\vec{u}}_{X$$YZ$

Park 변환(Robert H. Park의 이름)은 XYZ 기준 프레임의 벡터를 DQZ 기준 프레임으로 변환한다. Park 변환의 1차 값은 벡터의 기준 프레임을 임의 주파수로 회전시키는 것이다. Park 변환은 신호의 주파수 스펙트럼을 이동시켜 임의 주파수가 이제 "dc"로 나타나고 이전 dc가 임의 주파수의 음으로 나타나도록 한다. 공원 변환 매트릭스는

${\$$}}&\sin {\좌(\theta \우)}&0\\-\sin {\\좌(\theta \우)$$}}&\cos {\reft(\theta \right)}&0\0&0&1\end{bmatrix$

여기서 θ은 임의의 Ω 주파수의 순간 각이다. XYZ 기준 벡터를 DQZ 기준 프레임으로 변환하려면 기둥 벡터 신호를 주차 변환 매트릭스로 미리 곱해야 한다.

${\$$DQZ}=K_{P}\cdot u_{X$$YZ$

그리고 DQZ 기준 벡터에서 XYZ 기준 프레임으로 다시 변환하려면 칼럼 벡터 신호를 역 Park 변환 매트릭스로 미리 곱해야 한다.

${\$$YZ}=K_{P}^{-1}\cdot u_{{}$$DQZ$

Clarke와 Park는 함께 DQZ 변환을 형성한다.

${\displaystyle K_{CP}=K_{P}\cdot K_{C}}}$

${\displaystyle \to {\bmatrix}\cos {\reft(\theta \오른쪽)}}&\sin {\좌(\theta \우)}&0\\-\sin {\\좌(\theta \우)}&\cos {\left(\theta \right)}&0\\0&0&1\end{bmatrix}}\cdot {\sqrt {\frac {2}{3}}}{\begin{bmatrix}1&{\frac {-1}{2}}&{\frac {-1}{2}}\\0&{\frac {\sqrt {3}}{2}}&-{\frac {\sqrt {3}}{2}}\\{\frac {1}{\sqrt {2}}}&{\frac {1}{\sqrt {2}}}&{\frac {1}{\sqrt {2}}}\end{bmatrix}}}$

${\displaystyle \to {\sqrt {\frac {2}{3}}{\\properties{bmatrix}\cos {\reft}\coses {\\reft(\ta \오른쪽)}}&\cos {\왼쪽(\theta -{\frac {2\pi }{3}}\오른쪽)}&\cos {\left(\theta +{\frac {2\pi }{3}}\right)}\\-\sin {\left(\theta \right)}&-\sin {\left(\theta -{\frac {2\pi }{3}}\right)}&-\sin {\left(\theta +{\frac {2\pi }{3}}\right)}\\{\frac{\sqrt{2}}:{2}}:{\frac {\sqrt{2}}:}{{2}}:}}{\prac{2}}:\sqrt{bmatrix}}}}}}$

역변환:

${\displaystyle K_{CP}^{)}={\sqrt{\frac{2}{3}}}{\begin{bmatrix}\cos;{\frac{\sqrt{2}}{2}}\\\cos{\left(\theta-{\frac{2\pi}{3}}\right)}&{\frac{\sqrt{2}}{2}}\\\cos{\left(\theta+{\frac{2\pi}{3}}\right)}&, -\sin{\left(\thet -\sin{\left(\theta \right)}& -\sin{\left(\theta-{\frac{2\pi}{3}}\right)}&{\left(\theta \right)}&.한 +{\frac{2\pi}{3}}\\오른쪽)}&#{\frac {\sqrt{2}}:{2}}\end{bmatrix}}}}$

ABC 기준 벡터를 DQZ 기준 프레임으로 변환하려면 열 벡터 신호를 DQZ 변환 매트릭스로 미리 곱해야 한다.

${\$$DQZ}=K_{CP}\cdot u_{{$$ABC$

그리고 DQZ 기준 벡터에서 ABC 기준 프레임으로 다시 변환하려면 칼럼 벡터 신호를 역 DQZ 변환 매트릭스로 미리 곱해야 한다.

${\$$ABC}=K_{CP}^{-1}\cdot u_{{$$DQZ$

이 변환을 더 잘 이해하기 위해 변환의 파생이 포함되어 있다.

파생

공원 변환 파생

파크 변환은 도트 제품의 개념과 벡터의 다른 벡터에 대한 투영에 기초한다. First, let us imagine two unit vectors, ${\displaystyle {\hat {u}}_{D}}$ and ${\displaystyle {\hat {u}}_{Q}}$ (the unit vectors, or axes, of the new reference frame from the perspective of the old reference frame), and a third, arbitrary, vector ${\displaystyle {\vec {v}}_{XY}}$. 두 개의 단위 벡터와 임의 벡터를 기존 기준 프레임에서 데카르트 좌표 관점에서 정의할 수 있다.

${\displaystyle {\hat{u}_{D}=\cos {\왼쪽(\theta \오른쪽)}}{\hat{u}_{X}+\sin {\왼쪽(\theta \오른쪽)}}{\hat{u}}_{Y}}$

${\displaystyle {\hat{u}_{Q}=-\sin {\\왼쪽(\theta \오른쪽)}}{\hat{u}_{X}+\cos {\왼쪽(\theta \오른쪽)}}{\hat{u}}_{Y}}$

${\$$Y}=v_{X}{\hat {u}_{X}+v_{{}$$Y}{\hat{u}}_{$$Y$

$여기$서 ${\displaystyle {\stackrel{}{^}}_{}}$ ${\displaystyle X_{}}$ ${\$ $및$ ${\displaystyle {\stackrel{}{^}}_{}}$ ${\displaystyle Y_{}}$ ${\$$Y}$은 구좌표계의 단위기준 벡터로서$$^ ${\displaystyle X_{}}$ ${\$$displaystyle \theta}$은 ${\displaystyle {\stackrel{}{^}}_{}}$ X {\$displaystyle {\u}$$_{$$X}}}$와 ${\displaystyle {\stackrel{}{^}}_{}}$ ${\displaystyle D_{}}$ ${\$}} 단위 벡터(즉, 두 기준 프레임 사이의 각도) 사이의 각도이다$$. 임의 벡터를 두 개의 새로운 단위 벡터에 각각 투영하는 것은 도트 제품을 암시한다.

${\displaystyle v_{D}={\hat {u}_{D}\cdot {\v}}{XY}}$

${\displaystyle \to \cos(\theta \right)}v_{X}+\sin(\theta \right)v_{Y}}$

${\displaystyle v_{Q}={\hat {u}_{Q}\cdot {\vec{v}_{XY}}$

${\displaystyle \to }$- ${\displaystyle \sin }$ ${\displaystyle }$ (${\displaystyle \theta }$ ) ${\displaystyle v_{}}$ X${\displaystyle {}_{}}$+ ${\displaystyle \cos }$ ${\displaystyle }$ (${\displaystyle \theta }$ ) ${\displaystyle v_{}}$ Y ${\$ -$\sin$ {\\$to$ (\theta \rift$)v_{X}+\cos {\\reft(\theta \right)}v_{Y$

그래서 $v{\displaystyle {}_{}}$ ${\displaystyle D_{}}$ ${\$는 v${\displaystyle {\stackrel{}{}}_{}}$→ ${\displaystyle X_{}}$ Y ${\$의 투영이다.$Y{\displaystyle {\stackrel{}{}}_{}}$$}}$ ${\displaystyle {\stackrel{}{^}}_{}}$ ${\displaystyle D_{}}$ ${\$ 축에$$$$, v Q ${\$는 $v{\displaystyle {\stackrel{}{}}_{}}$→ ${\displaystyle X_{}}$ ${\displaystyle Y_{}}$ ${\$}의 투영이다.$Y{\displaystyle {\stackrel{}{}}_{}}$$}}$ ${\displaystyle {\stackrel{}{^}}_{}}$ ${\displaystyle Q_{}}$ ${\$ 축$$ 위에$$. $이러한{\displaystyle {}_{}}$ 새로운 벡터 구성 요소인 v ${\displaystyle D_{}}$ ${\$와 ${\displaystyle v_{}}$ $Q{\displaystyle {}_{}}$ ${\$는 함께 새로운 $벡터{\displaystyle {\stackrel{}{}}_{}}$ v${\displaystyle {\stackrel{}{}}_{}}$→ ${\displaystyle D_{}}$ ${\displaystyle Q_{}}$ ${\$를 구성한다$.$$DQ$ 원래의 벡터 $v{\displaystyle {\stackrel{}{}}_{}}$→ X ${\displaystyle Y_{}}$ ${\$$새로운$ DQ 기준 프레임의 측면에서$$ Y$}.$

위의$$ 양각 $\theta {\displaystyle }$ ${\displaystyle \theta }$이(가) 새 DQ 기준 프레임으로 전환될 때 임의 벡터가 뒤로 회전하는 원인이 된다는 점에 유의하십시오. 즉, 새로운 기준 프레임에 대한 그것의 각도는 이전 기준 프레임에 대한 그것의 각도보다 작다. 벡터가 아닌 기준 프레임이 앞으로 회전했기 때문이다. 실제로 기준 프레임의 전방 회전은 벡터의 마이너스 회전과 동일하다. 3상 전기 시스템과 같이 구형 기준 프레임이 전방으로 회전하는 경우, 결과 DQ 벡터는 정지 상태를 유지한다.

위의 연산은 단일 행렬 방정식으로 요약할 수 있다.

${\$$DQ}={\begin{bmatrix}\cos {\왼쪽(\$$theta \오른쪽)$$}}&\sin {\좌(\theta \우)\\-\sin {\좌(\theta \우)$$}}&\cos {\reft(\theta \right)}\$end{$bmatrix}\cdot {\v}_{XY$

이 텐서는 3차원 문제로 확장될 수 있으며, 여기서 회전하는 축은 영향을 받지 않는다. 다음 예에서 회전은 Z축에 관한 것이지만 어떤 축도 선택할 수 있었다.

${\$$}}&\sin {\좌(\theta \우)}&0\\-\sin {\\좌(\theta \우)$$}}&\cos {\reft(\theta \right)}&0\0&0&1\end{bmatrix$

선형 대수학적 관점에서 이것은 단순히 z축에 대한 시계방향 회전이며, 수학적으로 삼각차각 공식에 해당한다.

Clarke 변환 파생

ABC 단위 기준 벡터

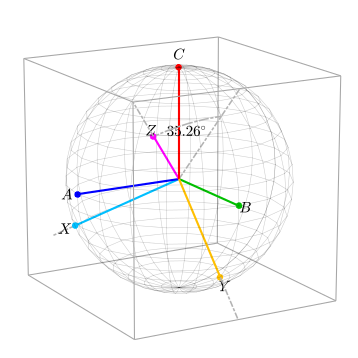
단위 벡터 A, B, C가 있는 3차원 공간을 고려한다. 아래 그림의 구체는 컨텍스트에 대한 참조 프레임의 스케일을 보여주는 데 사용되며, 박스는 회전 컨텍스트를 제공하는 데 사용된다.

일반적으로 전기공학(또는 3상 시스템을 사용하는 다른 맥락)에서는 3상 구성요소를 2차원적 시각으로 나타낸다. 그러나 세 단계가 독립적으로 변할 수 있다는 점을 감안할 때, 그들은 정의상 서로 직교한다. 이는 위의 그림과 같이 3차원적 관점을 내포하고 있다. 그래서 2차원적 원근법은 정말로 평면상에 3차원적 현실의 투영법을 보여주고 있다.

3상 문제는 일반적으로 이 평면 내에서 작동하는 것으로 설명된다. 현실적으로 문제는 균형상 문제(즉_A, v + v_C + v_B + v = 0)와 순 벡터일 가능성이 높다.

${\displaystyle {\vec{v}=v_{A}{\hat{u}}_{A}+v_{B}{\hat {u}_{B}+v_{C}{\hat {u}_{C}}{\hat {u}_{C}}}$

항상 이 비행기에 타고 있어

AYC' 단위 벡터

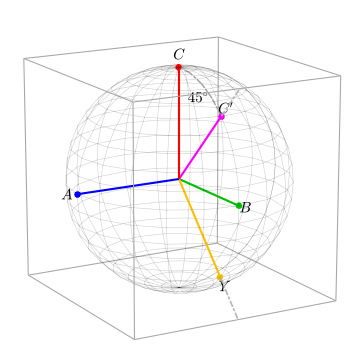
클라크 변환을 구축하기 위해 실제로 Park 변환을 두 단계로 나눠 사용한다. 우리의 목표는 상자 모서리로 C축을 회전시키는 것이다. 이렇게 하면 회전된 C축이 위에서 언급한 2차원 원근의 평면에 직교하게 된다. Clarke 변환을 구축하기 위한 첫 번째 단계는 A축에 대한 ABC 기준 프레임을 회전시켜야 한다. 그래서 이번에는 1이 공원 변환의 첫 번째 요소가 될 것이다.

${\displaystyle K_{1}={\begin{bmatrix}1&0\\\0&\cos {\\좌측(-{\frac {}\pi }}}{4}\우측)}}&\sin {\왼쪽{\frac {\pi }{4}}\오른쪽)}}\\0&-\sin {\frac{\frac {}{4}}\오른쪽)}}&\cos{\frac{\pi }{4}\오른쪽)\end{bmatrix}}}$

${\displaystyle \to {\begin{bmatrix}1&0&0\\0&{\frac {1}{\sqrt {2}}}&-{\frac {1}{\sqrt {2}}}\\0&{\frac {1}{\sqrt {2}}}&{\frac {1}{\sqrt {2}}}\end{bmatrix}}}$

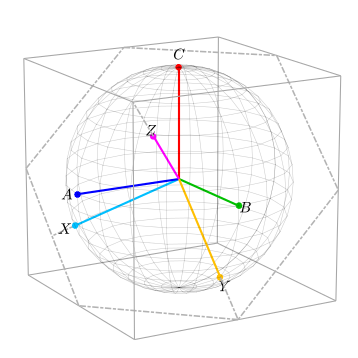
다음 그림은 어떤 벡터가 K₁ 행렬에 의해 사전 곱해질 때 ABC 기준 프레임이 AYC의 기준 프레임으로 회전하는 방법을 보여준다. C'와 Y축은 현재 박스 가장자리의 중간점을 가리키고 있지만, 기준 프레임의 크기는 변하지 않았다(즉, 구체는 커지거나 줄어들지 않았다).이는₁ K 텐서의 규격이 1:K₁ = 1이기 때문이다. 이것은 ABC 기준 프레임의 벡터가 AYC 기준 프레임으로 회전할 때 동일한 크기를 계속 갖는다는 것을 의미한다.

XYZ 단위 기준 벡터

다음으로, 다음의 텐서는 Y축에 대하여 새로운 Y축에 대한 벡터를 시계 반대 방향으로 회전시킨다(C'축이 상자의 모서리를 향하도록 각도를 선택했다).:

${\displaystyle K_{2}={\begin{bmatrix}\cos {\reft(\theta \right)}&0&-\sin(\theta \right)}\\0&1&0\\\sin {\왼쪽(\theta \오른쪽)&0&\cos {\왼쪽(\theta \오른쪽)\end{bmatrix}}}}$

${\displaystyle \theta }$= ${\displaystyle {\cos }^{}}$ -${\displaystyle 1^{}}$ ${\displaystyle {}^{}}$(${\displaystyle \sqrt{\frac{2}{}}}$ 3${\displaystyle \sqrt{}}$)${\displaystyle }$→ ${\displaystyle {35.26}^{}}$ ${\displaystyle {\circ }^{}}$ ${\$35.$26^{\cape$ $\},$

또는

${\displaystyle K_{2}={\begin{bmatrix}{\sqrt {\frac {2}{3}}}&0&-{\frac {1}{\sqrt {3}}}\\0&1&0\\{\frac {1}{\sqrt {3}}}&0&{\sqrt {\frac {2}{3}}}\end{bmatrix}}}$.

구 중심에서 상자 가장자리의 중간점까지의 거리는 √2이지만 구 중심에서 상자 가장자리까지의 거리는 √3이다. 그것이 바로 35.26° 각도가 나온 것이다. 각도는 도트 제품을 사용하여 계산할 수 있다. Let ${\displaystyle {\vec {m}}=\left(0,{\frac {\sqrt {2}}{2}},{\frac {\sqrt {2}}{2}}\right)}$ be the unit vector in the direction of C' and let ${\displaystyle {\vec {n}}=\left({\frac {1}{\sqrt {3}}},{\frac {1}{\sqrt {3}}},{\frac {1}{\s$$qrt {3}}}\right)}$ be a unit vector in the direction of the corner of the box at ${\displaystyle {\vec {n}}=\left(1,1,1\right)}$. Because ${\displaystyle {\vec {m}}\cdot {\vec {n}}= {\vec {m}} {\vec {n}} \cos \theta ,}$ where ${\displaystyle \theta }$${\displaystyle \theta}$은(는) $m{\displaystyle \stackrel{}{}}$→ ${\$과(와) $n{\displaystyle \stackrel{}{}}$→${\displaystyle {\vec {n}$ 사이의$$ 각도임.

${\displaystyle \left(0,{\frac {\sqrt {2}}{2}},{\frac {\sqrt {2}}{2}}\right)\cdot \left({\frac {1}{\sqrt {3}}},{\frac {1}{\sqrt {3}}},{\frac {1}{\sqrt {3}}}\right)=\cos \theta }$

${\displaystyle \cos \theta =0+{\frac{\sqrt{3}}}{2}{\\sqrt{3}}}}}{2}{\sqrt{3}}}}}}}}}{\sqrt{\sqrt{{}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

${\displaystyle \theta =\cos ^{-1}\left\sqrt {\frac {2}{3}}\오른쪽)}$

$\displaystyle \theta =35.26^{\reason }}$

K₂ 행렬의 표준도 1이므로 K 행렬이₂ 미리 곱한 벡터의 크기 역시 변경되지 않는다.

영점면

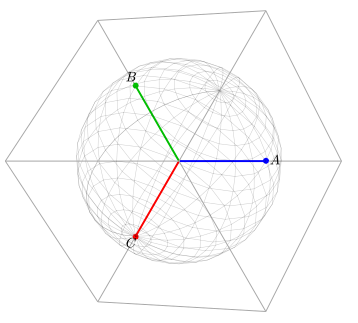
이 지점에서 Z축은 이제 공통 모드 성분이 없는 ABC 벡터를 찾을 수 있는 평면에 직교한다. 균형 잡힌 ABC 벡터 파형(공통 모드가 없는 벡터)은 이 평면을 돌아다닌다. 이 평면은 영점면이라고 불릴 것이며 육각형 윤곽으로 아래에 표시된다.

X와 Y 기준 벡터는 영면에 있다. X 축은 A 축의 영점 평면 투영과 평행하다는 점에 유의하십시오. X축은 A축이 영점 평면에 투영되는 것보다 약간 크다. √3/2 인수로 더 크다. 임의 벡터는 이 ABC 기준 프레임에서 XYZ 기준 프레임으로 변환하여 크기를 변경하지 않았다(즉, 구체는 크기를 변경하지 않았다). 이것은 클라크 변환의 파워 인바리어스 형태에 적용된다. 다음 그림은 ABC와 XYZ 기준 프레임의 공통 2차원 관점을 보여준다.

벡터의 크기가 바뀌지 않았지만, 벡터의 구성 요소의 크기(즉, X와 Y 구성 요소가 A, B, C 구성 요소보다 길다)는 것은 이상해 보일 수 있다. 아마도 이것은 공통 모드가 없는 벡터의 경우, Z 성분이 0이기 때문에 세 가지 값(A, B, C 성분)을 표현하는 데 필요한 것이 이제는 2개(X, Y 성분)만 들어간다는 것을 생각하면 직관적으로 이해할 수 있을 것이다. 따라서 X와 Y 성분 값은 보정하기 위해 더 커야 한다.

텐서 조합

파워 인바리어트 Clarke 변환 매트릭스는 K₁ 텐서와 K₂ 텐서의 조합이다.

KC)[230− 1301013023]⏟ K2⋅[100012− 1201212]⏟ K1{\displaystyle K_{C}=\underbrace{\begin{bmatrix}{\sqrt{\frac{2}{3}}}&0&, -{\frac{1}{\sqrt{3}}}\\0&, 1&, 0\\{\frac{1}{.\sqrt{3}}}$&0&{\sqrt {\frac {2}{3}}}\end{bmatrix}} _{K_{2}}\cdot \underbrace {\begin{bmatrix}1&0&0\\0&{\frac {1}{\sqrt {2}}}&-{\frac {1}{\sqrt {2}}}\\0&{\frac {1}{\sqrt {2}}}&{\frac {1}{\sqrt {2}}}\end{bmatrix}} _{K_{1}}}$,

또는

${\displaystyle K_{C}={\sqrt {\frac {2}{3}}}\cdot {\begin{bmatrix}1&-{\frac {1}{2}}&-{\frac {1}{2}}\\0&{\frac {\sqrt {3}}{2}}&-{\frac {\sqrt {3}}{2}}\\{\frac {1}{\sqrt {2}}}&{\frac {1}{\sqrt {2}}}&{\frac {1}{\sqrt {2}}}\end{bmatrix}}}$

→[26− 16− 16012− 12131313]{\displaystyle \to{\begin{bmatrix}{\frac{2}{\sqrt{6}}}&-{\frac{1}{\sqrt{6}}}&-{\frac{1}{\sqrt{6}}}\\0&,{\frac{1}{\sqrt{2}}}&-{\frac{1}{\sqrt{2}}}\\{\frac{1}{\sqrt{3}}}&{\frac{1}{\sqrt{3}}}&a.융점.{\frac{1}{\sqrt${3}}\end{bmatrix$

통과를 곱할 때 K_C 행렬의 아래쪽 행은 1/3이 아니라 1/2/3이라는 점에 유의하십시오(Edith Clarke는 전력 변수 사례에 1/3을 사용함). Z 성분은 A, B, C 성분의 평균이 아니다. 맨 아래 행 요소만 1/3로 변경하면 Z축을 따라 구가 찌그러진다. 즉, Z 성분이 X 및 Y 성분과 동일한 스케일링을 가지지 않을 것이다.

사물이 위에 쓰여 있듯이 클라크 변환 매트릭스의 규범은 여전히 1인데, 이는 ABC 벡터만 회전할 뿐 스케일은 하지 않는다는 것을 의미한다. 클라크의 원래 변신은 말할 수 없다.

(행렬_C 곱셈을 통해) K의 역행성이라는 것을 쉽게 확인할 수 있다.

${\displaystyle K_{C}^{-1}={\begin{bmatrix}{\frac {2}{\sqrt {6}}}&0&{\frac {1}{\sqrt {3}}}\\-{\frac {1}{\sqrt {6}}}&{\frac {1}{\sqrt {2}}}&{\frac {1}{\sqrt {3}}}\\-{\frac {1}{\sqrt {6}}}&-{\frac {1}{\sqrt {2}}}&{\frac {1}{\sqrt {3}}}\end{bmatrix}}}$

전력변수형식

X 축이 A 축의 영점 평면에 투영되도록 Clarke 변환 매트릭스를 스케일링하는 것이 바람직할 때도 있다. 이를 위해 component2/3의 스케일링 계수와 √1/라디칼을^[why?] 0 성분으로 균일하게 적용하여 전력 변수 Clarke 변환 행렬을 구한다.

${\displaystyle K_{\hat {C}}={\sqrt {\frac {2}{3}}}\cdot \underbrace {{\sqrt {\frac {2}{3}}}\cdot {\begin{bmatrix}1&-{\frac {1}{2}}&-{\frac {1}{2}}\\0&{\frac {\sqrt {3}}{2}}&-{\frac {\sqrt {3}}{2}}\\{\frac {1}{2}}&{\frac {1}{2}}&{\frac {1}{2}}\end{bmatrix}}} _{K_{C}}}$

${\displaystyle \to {\frac {2}{3}}{\begin{bmatrix}1&-{\frac {1}{2}}&-{\frac {1}{2}}\\0&{\frac {\sqrt {3}}{2}}&-{\frac {\sqrt {3}}{2}}\\{\frac {1}{2}}&{\frac {1}{2}}&{\frac {1}{2}}\end{bmatrix}}}$

또는

KC^)({\displaystyle K_{\hat{C}}={\begin{bmatrix}{\frac{2}{3}}&-{\frac{1}{3}}&-{\frac{1}{3}}\\0&,{\frac{1}{\sqrt{3}}}&-{\frac{1}{\sqrt{3}}}\\{\frac{1}{3}}&{\frac{1}{3}}&{\frac{1}{3}}\end{bmatrix}.}}.

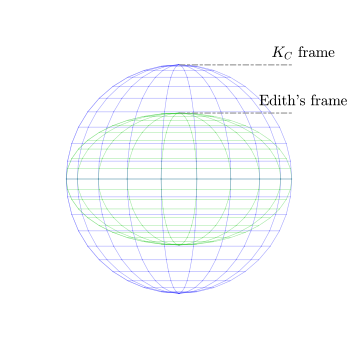
이것은 반드시 아래와 같이 sphere2/3의 인수로 구를 수축시킬 것이다. 이 새로운 X축은 정확히 A축이 영점 평면에 투영된 것이라는 점에 유의하십시오.

전력변수 클라크 변환의 경우, 임의 벡터의 크기는 ABC 기준 프레임에서보다 XYZ 기준 프레임에서 작지만(변환 표준은 √2/3) 개별 벡터 성분의 크기는 동일하다(공통 모드가 없는 경우). 예를 들어, 신호는

${\displaystyle {\bmatrix}A\\B\\C\end{bmatrix}={\begin{bmatrix}\cos(\\eft(\omega t\오른쪽)}}\\\cos(\omega t-{\frac {2\pi}{3}}\오른쪽)}}\\cos {\reft(\omega t+{\frac {2\pi }{3}\오른쪽)\end{bmatrix}}}}$

XYZ 기준 프레임에서

${\$$Y\\Z\end{bmatrix}={\begin{bmatrix}\cos(\왼쪽(\omega t\오른쪽)$$}}\\\cos(\omega t-{\frac {}}{2}}\오른쪽)$$}}\\0\end{bmatrix$

원본 구성 요소:1의 요소는 같은 크기 새로운 벡터. 많은 경우 그power-variant 클라크 변환의, 이것은 유리한 품질이다.

DQZ 변환

그 DQZ 변환 2차동 모드 구성 요소(즉, X, Y)과 동상 모드 구성 요소(즉, Z)로ABC-referenced 벡터 변환한 다음 어떤 일정한 각도에서 Z축에 대한 기준틀을 회전하려면 공원 변환을 적용하는 클라크 변환을 사용한다. 는 회전의 벡터로 직접 맞추어 져 있습니다 그 X요소가 되D성분과, 직접적인 구성 요소에 직각 각도에 있는 Y요소가 된 성분입니다. 그 DQZ 대해 변환은

${\displaystyle K_{CP}=K_{P}\cdot K_{C}}}$

→[왜냐면 ⁡(θ)죄 ⁡(θ)0− 죄 ⁡(θ)오리온 ⁡(θ)0001]⋅ 23[1− 12− 12032− 32121212]{\displaystyle \to{\begin{bmatrix}\cos{\left(\theta \right).}&\sin{\left(\theta \right)}&, 0\\-\sin{\left(\theta \right).}&\cos{\left(\theta \right)}&, 0\\0&, 0&, 1\end{bmatrix}}\cdot{\sqrt{\frac{2}{3}}}{\begin{bmatrix}1&,{\frac{)}{2}}&{\frac{)}{2}}\\0&,{\frac{\sqrt{3}}{2}}&-{\frac{\sqrt{3}}{2}}\\{\frac{1}{\sqrt{2}}}&{\frac{1}{\sqrt{2}}}&{\frac{1}{\sqrt{2}}}\end{bmatrix}}}.

코드 구현

연산 효율을 위해서는 클라크와 파크 변환을 분리해서 유지하면서 하나의 변환으로 결합하지 않는 것이 이치에 맞는다.

파워 인바리어스 클라크 변환의 연산 효율적 구현은

X = (2 * A – B – C) * (1 / sqrt(6)); Y = (B – C) * (1 / sqrt(2)); Z = (A + B + C) * (1 / sqrt(3)); 

그 반대인 반면에.

A = (1 / sqrt(3)) * Z; B = A – (1 / sqrt(6)) * X; C = B – (1 / sqrt(2)) * Y; B += (1 / sqrt(2)) * Y; A += (sqrt(2 / 3)) * X; 

전력 변수 클라크 변환의 연산 효율적 구현은

X = (2*A – B – C) * (1 / 3); Y = (B – C) * (1 / sqrt(3)); Z = (A + B + C) * (1 / 3); 

그 반대인 반면에.

A = X + Z; B = Z – (1 / 2) * X; C = B – (sqrt(3) / 2) * Y; B += (sqrt(3) / 2) * Y; 

분명히 상수 계수는 미리 계산될 수 있다.

Park 전환의 컴퓨팅 효율적 구현은

공동의 = cas(세타); si = 죄를 짓다(세타);  D = 공동의*X + si*Y; Q = 공동의*Y - si*X; 

그 반대인 반면에.

공동의 = cas(세타); si = 죄를 짓다(세타);  X = 공동의*D - si*Q; Y = si*D + 공동의*Q; 

파크 변환과 역 파크 변환을 모두 사용할 경우 계산하는 것이 타당하다.

예

전기 시스템에서는, 매우 자주 A, B, C 값이 순 벡터가 회전하는 방식으로 진동한다. 균형 잡힌 시스템에서 벡터는 Z축을 중심으로 돌고 있다. 이러한 회전으로 인해 abc 값에서 대부분의 변화가 취소되고 보다 미세한 변형이 더 명백해지도록 기준 프레임을 회전시키는 것이 매우 자주 도움이 된다. 이것은 현재 시스템을 선형 시간 변화 시스템으로 변환하기 때문에 믿을 수 없을 만큼 유용하다.

DQZ 변환은 세 개의 개별 정현상 위상 수량을 정현상 위상 수량과 동일한 각도로 회전하는 두 축에 투영하는 것으로 기하학적 용어로 생각할 수 있다.

위에 나타낸 것은 동기식 기계의 스테이터에 적용되는 DQZ 변환이다. 세 개의 권선이 120도로 분리되어 있다. 3상 전류는 크기가 같으며, 120도씩 서로 분리된다. 3상 전류는 해당 위상 전압을 $\Delta {\displaystyle }$ ${\displaystyle \delta }$만큼 지연시킨다$.$ DQ 축은 위상 전압 및 전류와 동일한 각도 속도인$$$\Omega {\displaystyle }$ ${\displaystyle \omega }$에 해당하는 각 속도로 회전하는 것으로 나타난다. D축은 기준으로 선택한 위상 A 권선과 함께$$ 각도 $\theta {\displaystyle }$= ${\displaystyle \Omega }$ ${\displaystyle t}$ ${\displaystyle \theta =\omega t}$을 만든다. 전류 ${\displaystyle I_{}}$ ${\$와 $I{\displaystyle {}_{}}$ ${\displaystyle Q_{}}$ ${\$는 일정한$$ dc량이다.

다른 변환과의 비교

박태환의 변신

당초 박 대표가 제시한 변혁은 위에서 제시한 변혁과 다소 차이가 있다. 박씨의 변환 q축은 d축, qd0보다 앞서 있으며, $\theta {\displaystyle }$ ${\displaystyle \theta }$각은$$ 다음과 같이 위상 a축과 q축 사이의 각이다.

${\displaystyle P={\frac {2}{3}}{\begin{bmatrix}\cos(\theta )&\cos(\theta -{\frac {2\pi }{3}})&\cos(\theta +{\frac {2\pi }{3}})\\\sin(\theta )&\sin(\theta -{\frac {2\pi }{3}})&\sin(\theta +{\frac {2\pi }{3}})\\{\frac {1}{2}}&{\frac {1}{2}}&{\frac {1}{2}}\end{bmatrix}}}$

그리고

${\displaystyle P^{-1}={\begin{bmatrix}\cos(\theta )&\sin(\theta )&1\\\cos(\theta -{\frac {2\pi }{3}})&\sin(\theta -{\frac {2\pi }{3}})&1\\\cos(\theta +{\frac {2\pi }{3}})&\sin(\theta +{\frac {2\pi }{3}})&1\end{bmatrix}}}$

D. 홈즈와 T. Lipo, 전력 변환기의 펄스 폭 변조: 원리 및 실습, Wiley-IEEE Press, 2003 및

P. 크라우스, O. 와신축과 S. 수드호프, 전기 기계 및 구동 시스템 분석, 2차 개정, 피스카타웨이, NJ: IEEE 프레스, 2002.

αβγ 변환

dqo 변환은 개념적으로 αβγ 변환과 유사하다. dqo 변환은 회전하는 2축 기준 프레임에 위상 수량을 투영하는 반면, αβγ 변환은 정지해 있는 2축 기준 프레임에 위상 수량을 투영하는 것으로 생각할 수 있다.

참조

인라인 참조

일반참조

참고 항목

• 대칭 성분
• ${\displaystyle \alpha }$ ${\displaystyle \beta }$ ${\displaystyle \gamma }$ ${\displaystyle \alpha \beta$\gamma \$gamma }$ 변환$$
• 벡터 제어(모터)