푸시다운 오토마톤

이 글은 검증을 위해 추가 인용문이 필요합니다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선하는 데 도움을 주십시오. 조달되지 않은 자재는 제거될 수 있습니다.출처 : '푸시다운 오토마톤'– 뉴스 · 신문 · 서적 · 학자 · JSTOR (2022년 4월) (이 템플릿 메시지 삭제 방법 및 삭제 시기 확인)

이론 컴퓨터 과학의 한 분야인 계산 이론에서 푸쉬다운 오토마톤(PDA)은 스택을 사용하는 오토마톤의 한 종류입니다.

푸시다운 오토마타는 기계로 계산할 수 있는 것에 대한 이론에서 사용됩니다.그것들은 유한 상태 기계보다 더 능력이 있지만 튜링 기계보다 더 능력이 떨어진다(아래 참조).결정론적 푸시다운 오토마타는 모든 결정론적 문맥 자유 언어를 인식할 수 있는 반면 비결정론적 문맥 자유 언어는 모든 문맥 자유 언어를 인식할 수 있으며, 전자는 파서 설계에 자주 사용된다.

"푸시다운"이란 작업은 상단 요소 이외에는 작동하지 않기 때문에 구내식당의 트레이 디스펜서처럼 스택이 "밀려 내려가는" 것으로 간주될 수 있다는 사실을 말합니다.반면 스택 자동화는 더 깊은 요소에 대한 액세스와 운영을 허용합니다.스택 오토마타는 푸시다운 ^[1]오토마타보다 훨씬 큰 언어 세트를 인식할 수 있습니다.네스트된 스택오토마톤은 풀액세스를 가능하게 하고 스택된 값을 단일 유한기호가 아닌 서브스택 전체로 할 수도 있습니다.

비공식적인 설명

유한 상태 기계는 입력 신호와 현재 상태만 확인합니다. 즉, 사용할 스택이 없습니다.이행에 따른 결과로서 새로운 상태가 선택됩니다.Pushdown Automaton(PDA)은 다음 두 가지 점에서 유한 상태 기계와 다릅니다.

1. 스택 상단을 사용하여 어떤 전환을 수행할지 결정할 수 있습니다.
2. 이행의 일부로서 스택을 조작할 수 있습니다.

푸시다운 오토마톤은 소정의 입력 문자열을 왼쪽에서 오른쪽으로 읽는다.각 단계에서 입력 기호, 현재 상태 및 스택 상단의 기호를 기준으로 테이블을 인덱싱하여 전환을 선택합니다.푸시다운 오토마톤은 이행의 일부로서 스택을 조작할 수도 있습니다.조작은 특정 기호를 스택의 맨 위로 푸시하거나 스택의 맨 위에서 팝업하는 것입니다.자동화는 스택을 무시하고 그대로 둘 수도 있습니다.

조합: 입력 기호, 현재 상태 및 스택 기호를 지정하면 자동화는 다른 상태로의 이행에 따라 선택적으로 스택을 조작(푸시 또는 팝)할 수 있습니다.

모든 상황에서 이러한 이행 액션이 1개라도 가능한 경우, 자동화는 결정론적 푸시다운 오토마톤(DPDA)이라고 불립니다.일반적으로 몇 가지 동작이 가능한 경우 자동화는 일반 또는 비확정론적 PDA라고 불립니다.지정된 입력 문자열은 여러 구성 시퀀스 중 하나로 비확정론적 푸시다운 자동화를 유도할 수 있습니다.입력 문자열 전체를 읽은 후 이들 중 하나가 수용 가능한 구성으로 이어질 경우, 후자는 th에 속한다고 합니다.자동화에 의해 받아들여지는 e언어.

형식적 정의

We use standard formal language notation: ${\displaystyle \Gamma ^{*}}$ denotes the set of finite-length strings over alphabet ${\displaystyle \Gamma }$ and ${\displaystyle \varepsilon }$ denotes the empty string.

PDA는 공식적으로 7 태플이라고 정의됩니다.

${\displaystyle M}$ ${\displaystyle =}$ (${\displaystyle Q}$ ,${\displaystyle \mathrm{\sigma }}$ , ${\displaystyle \mathrm{\gamma }}$, 0 ,${\displaystyle {q\mathrm{}}_{}}$0 ,${\displaystyle Z}$ ,${\displaystyle F}$) ( $displaystyle$ M = ( $Q$, \ $Sigma$, \ $Gamma$, \ displaystyle , $q$_ {$0$ ,$Z$ , $F$) 。여기서$$,

• $(\displaystyle$ Q$)$는 유한한 상태의 집합입니다.
• $δ(\displaystyle$\Sigma$$)는 입력 알파벳이라고 하는 유한 집합입니다.
• $δ(\displaystyle$\Gamma$$)는 스택알파벳이라고 불리는 유한세트입니다.
• ${\$ {$displaystyle$ \ delta$$${\displaystyle \}}$는${\displaystyle }$Q${\displaystyle }$× (${\displaystyle \mathrm{\sigma }}$ { ${\displaystyle {\mathrm{}}^{}}$ ${\displaystyle \}}$ ) ×$Q$ ( \ $sigma$\ $cup$\ { \ $varepsilon \$ $}$ \ $times$ \$Gamma ^$ { * } )의 유한 서브셋입니다$.$
• ${\displaystyle {q\mathrm{}}_{}}$ 0$(\displaystyle q_{$0}\$in$ Q$)$는 시작 상태입니다.
• ${\displaystyle }$Z${\displaystyle \mathrm{\gamma }}$display \ $display Z$\ $in$ \ Gamma $}$는 초기 스택 기호입니다.
• ${\displaystyle Fq}$Q(\$displaystyle$ F$\subseteq)$는 수용 상태의 집합입니다.

요소$({\displaystyle p}$ , a${\displaystyle }$,${\displaystyle A}$ ,${\displaystyle q}$ ,${\displaystyle }$α ) ${\displaystyle \in }$ ${\$ （$p$ ,$a$ ,$A$ ,$q$ , \$alpha$）\$in \delta$}는 M$${\$displaystyle$ M$\}$의 천이입니다.$입력{\displaystyle }$ ${\displaystyle \mathrm{P}}$ ${\displaystyle \in }$$$ { $displaystyle$ p$\in$ Q$\}$의 의미를 가집니다.$({displaystyle$ A$\in \Gamma$$\}$는 최상위 스택 기호로서$,$ $상태$를$$$q$\$displaystyle$q$\},$ $pop{\displaystyle }$ A$\backslash$$displaystyle$ A로 $변경$하고, ${\displaystyle \mathrm{\alpha }}$$$ display${\displaystyle }$display \ $displaystyle \in \Gamma$ ${\displaystyle ^\{*\}}$를 눌러 $대체$할 수 있습니다$.)$변환 관계는 PDA가 입력으로부터 문자를 읽거나 입력이 ^{[citation needed]}변경되지 않은 상태로 진행할 수 있도록 공식화하기 위해 사용됩니다.

많은^{[2]: 110} 텍스트에서 전이 관계는 (등가) 공식화로 대체된다.

• ${\$ {$displaystyle$ \ delta$$}는 Q${\displaystyle }$× ($ε$ ${\displaystyle \{}$ ${\displaystyle )}$ } ) ×$γ$\ $times$$$( \ $Sigma$ \$cup$ \ { \$varepsilon$ \ $})\times$ \ Gamma$$$$$}$을$Q$×${$의 유한 $서브셋$에 매핑하는 $변환{\displaystyle }$ 함수입니다$.$

$여기$서 ${\displaystyle \S }$ ( ${\displaystyle p}$,${\displaystyle a}$ , A$$) { $displaystyle \delta ($ p ,$a$ , $A$) 에는$$, 스택상의$$A$${\$displaystyle$ p$$}$상태$에서 가능한 모든 액션이 포함되어 있습니다.또$,$ 입력상의 A {\$displaystyle$ a$}$를 $읽어냅니다{\displaystyle }$.${\displaystyle 예}$를 들어${\displaystyle ,}$(${\displaystyle q,}$a${\displaystyle }$) ${\displaystyle =}${ ($,$ ${\displaystyle B}$${\displaystyle A}$ ) $=$ \ { ($q, a,$A)\{(q,$B)\}$${\displaystyle \in }${${\displaystyle }$(${\displaystyle q}$, B A ) ${\displaystyle \}}$ ,${\displaystyle }$(${\displaystyle q,}$ ${\displaystyle BA}$ ) $style$ ${\displaystyle P}$,$$A )${\displaystyle 。}$$$\$delta$ 이 정의에서는 유한성이 필수적입니다$.$

계산

푸시다운 자동화의 의미를 공식화하기 위해 현재 상황에 대한 설명이 도입된다.$Q\times \Sigma ^{*}\times \Gamma$^{*}\$times$ \$displaystyle$M의 $현재{\displaystyle }$ 상태를 포함한 임의의 3-tuple${\displaystyle }$($p,$,${\displaystyle {\mathrm{}}^{})\in {\mathrm{}}^{}}$ × ${\displaystyle {}^{}}$ \ $displaystyle$( p, $w,$ \ $beta$) ${\$ \ Gamma ^{*}$${ { { { { { {$${ { is$$ is is is is is is is is is is any any any any any an an any any any any any any any any any any any any any any any any any any any any이행관계 ${\$ { $display$style \ $delta$} $trans$ 、$$M \ $display style$\ $vdash$_ { $M$} $of$ descript descript the the the the theionsionsionsionsionsionsionsions ${\displaystyle {the}_{}}。{\displaystyle {}_{}}$${\displaystyle \mathrm{명령어}(p}$ , ${\displaystyle a}$, ${\displaystyle A}$, ${\displaystyle q}$, α ) $∈$ \ $displaystyle ($${\displaystyle p}$ ,$a$ , A ,$$${\displaystyle q}$ , \$alpha )$\ $in$ \ delta$$$$}${\displaystyle m_{}M{}_{}}$(${\displaystyle q}$ , ${\displaystyle x}$ ,$$ ) \ $displaystyle ($ p ,$A$ \$gamma$ ) \ $dash$ { $Q$, \ dash $}$$mma$

일반적으로 푸시다운 오토마타는 특정 순간 설명$({\displaystyle p}$ ,${\displaystyle w}$ ,${\displaystyle }$β )$${$display$style ($p$ ,$w$ , \ $beta$ )$$} 에는$$ 몇 가지 가능한 단계가 있을 수 있다는 것을 의미합니다.이러한 단계는 모두 계산에서 선택할 수 있습니다.각 단계에서 위의 정의를 사용하면 항상 단일 기호(스택의 상단)가 팝업되어 필요한 수의 기호로 대체됩니다.그 결과 스택이 비어 있을 때는 스텝이 정의되지 않습니다.

푸시다운 오토마톤의 연산은 스텝의 시퀀스입니다.연산은 초기 $상태{\displaystyle {}_{}}$ ${\displaystyle {q\mathrm{}}_{}}$ 0$({$0$$})에서 시작되며, 스택의 초기 스택 $기호{\displaystyle }$Z({$displaystyle$Z})와$$ 입력 테이프의 $문자열{\displaystyle }$w({$displaystyle$w})로$$ 시작됩니다.따라서 초기 설명$q 0, w,$을 사용하여 허용 모드는 두 가지가 있습니다.푸쉬다운 오토마톤은 최종 상태로 받아들여집니다.즉, 입력 내용을 읽은 후 오토마톤이 승인 상태에 도달하거나(${\displaystyle }$$${\$displaystyle$ F$}),$ 또는 빈 스택$($ by {\$displaystyle \varepsilon})$으로 받아들여집니다.즉, 입력 내용을 읽은 후 오토마톤이 스택을 비웁니다.첫 번째 수용 모드에서는 내부 메모리(스테이트)가 사용되고 두 번째 수용 모드에서는 외부 메모리(스택)가 사용됩니다.

정식으로 정의하다

1. $L$ ${\displaystyle (}$M ) $=$ { ${\displaystyle w}$ ${\displaystyle \in }$ ${\displaystyle {\sigma \mathrm{}}_{}}$ ${\displaystyle {\ast }^{}{}^{}{}_{}}$ （${\displaystyle {}_{}q}$0 ,${\displaystyle w}$ , Z )$f$M${\displaystyle {}_{}^{}{f}_{}^{}}$ ${\displaystyle （}$ f ,${\displaystyle }$）$$ ${\displaystyle w}$ \ $in$\ Sigma ^ { * } ( $q _$ 0 $, w$, $Z$) \ $vdash$_ { M }$（$ \ $vilon$ ） 、 $。$
2. ${\displaystyle N}$(${\displaystyle M}$ ) ${\displaystyle =}$ { ${\displaystyle w}$ ${\displaystyle \in }$ ${\displaystyle {\sigma \mathrm{}}_{}}$ ∗ ${\displaystyle \ast {}^{}}$ （${\displaystyle {}_{}q}$0 ,${\displaystyle w}$ , ${\displaystyle {}_{}}$ )${\displaystyle {}_{}^{}}$ M ${\displaystyle q}$ ${\displaystyle （}$ q ,$0$ ,${\displaystyle }$w , Z$){$ $style$N ( M ) = \ { w$$\$in$ \ Sigma ^ { * } ( $q _ 0$, w , Z ) \ $vdash$_ { M $}$（ \ $arevilon$） 、 \ 。

${\displaystyle {여기}_{}^{}}$서${\displaystyle {}_{}^{}}$M ${\$ { $display$style \ $vdash _${ $M$$}^{$ * }은$$$$ 스텝 관계$M$의 재귀적 및 전이적 폐쇄를 나타냅니다.즉, 연속되는 스텝의 수(0, 1 또는 그 이상)를 의미합니다.

각각의 푸시다운 오토마톤에 대해서, 이 2개의 언어는 관계가 없습니다.동일할 수도 있지만, 통상은 그렇지 않습니다.자동 사양에는 의도된 수용 모드도 포함되어야 합니다.모든 푸시다운 오토마타를 인계받으면 두 허용 조건 모두 동일한 언어 패밀리를 정의합니다.

정리.각 푸시다운 $오토마톤{\displaystyle }$ M$({displaystyle$M})에$$ 대해 L${\displaystyle (M)}$ $=$이 $되도록{\displaystyle }$ 푸시다운 $오토마톤{\displaystyle {}^{}}$ M$({$$displaystyle$ M$')$을 구성할 수 있으며, 각 푸시다운 $오토마톤{\displaystyle }$M({$displaystyle$ M$')$에 대해 L$(M$) = N$(M$이 되도록 푸시다운 오토마톤 M({displaystyle M')을 $구성$할 수 있습니다${\displaystyle {.}^{}}$$=$

예

다음으로 언어${\displaystyle }${${\displaystyle 0^{}}$ ${\displaystyle {}^{}{\mathrm{}}^{}}$ 1 ${\displaystyle n^{}n}$ n ${\displaystyle 0}$ 0${\displaystyle \}}${ $displaystyle$\ { $0$^ { $n$} $1 ^$ { n } \ mid $n$ \ $geq$ 0$$\ } 를 최종 상태로 인식하는 PDA 의 정식 설명을 나타냅니다.

${\displaystyle M}$ ${\displaystyle =}$ (${\displaystyle }$Q ,${\displaystyle \text{σ}\mathrm{}}$ , ,${\displaystyle \text{γ}\mathrm{}}$ , ,${\displaystyle {q\mathrm{}}_{}}$0 ,${\displaystyle \text{Z}}$ ,${\displaystyle \text{F}}$ )$${ $displaystyle$ M = ( $Q ,$ \ $Sigma ,$ \ $Gamma ,$ \ displaystyle } 、 \ displaystyle $M$= ( Q , \ Sigma , \ \ \ Gamma , \ 、 \ \ { $0$, \ \ 0 , \ $F$)$$} 、 \ Z , \ F ) 。 。 、 。 。 。 。 。

• 상태: ${\displaystyle Q=\{p,q,r\}}$
• 입력 알파벳: ${\displaystyle \Sigma =\{0,1\}}$
• 스택 알파벳: $(\displaystyle \Gamma =\{A,Z\})$
• 시작 상태: ${\displaystyle q_{0}=p}$
• 시작 스택 기호: Z
• 수용 상태: ${\displaystyle F=\{r\}}$

이행관계$$©(\$displaystyle \delta)$는 다음 6가지 명령으로 구성됩니다.

${\displaystyle (p}$ ,${\displaystyle 0}$ ,${\displaystyle Z}$ ,${\displaystyle p}$ , ${\displaystyle AZ}$) ( $displaystyle ( p$ , $0 , Z$ ,$p$ , $AZ )$,

${\displaystyle (p}$ ,${\displaystyle 0}$ ,${\displaystyle A}$ ,${\displaystyle p}$ , ${\displaystyle A}$)$$( $displaystyle ( p$ , $0 , A$ ,$p$ , $AA )$,

${\displaystyle (p}$ , ${\displaystyle 、}$ ${\displaystyle Z}$ ,${\displaystyle q}$ ,${\displaystyle Z}$ ) {$displaystyle$( $p$, \ $epsilon , Z$ ,$q$ , $Z$)$$} ,

${\displaystyle (p}$ , ${\displaystyle 、}$ ${\displaystyle A}$,${\displaystyle q}$ ,${\displaystyle A}$) { $displaystyle$( $p$, \ $epsilon , A$ ,$q$ ,$A$ )$$} ,

${\displaystyle (\mathrm{q}}$ ,${\displaystyle }$1 ,${\displaystyle A}$ ,${\displaystyle q}$ ,${\displaystyle }$" )$$( $displaystyle ( q$ , 1,$A$ ,$q$ , \ $epsilon$) $\}$ ,

${\displaystyle (q}$ , "${\displaystyle }$,${\displaystyle }$Z ,${\displaystyle r}$ ,${\displaystyle Z}$ )$${ $displaystyle ( q$ , \ $epsilon , Z$ ,$r$ , $Z$)$$} 。

즉, 처음 두 명령은 상태 p에서 기호 0을 읽을 때마다 1개의 A가 스택에 푸시된다고 합니다.다른 A 위에 누르는 기호 A를 AA로 대체한다(또한 마찬가지로 기호 A를 Z 위에 누르는 것도 마찬가지).

세 번째와 네 번째 명령은 자동화가 언제든지 상태 p에서 상태 q로 이동할 수 있다고 말합니다.

다섯 번째 명령에서는 상태 q에서 기호 1을 읽을 때마다 A가 하나 팝된다고 합니다.

마지막으로, 여섯 번째 명령은 스택이 단일 Z로 구성되어 있는 경우에만 기계가 상태 q에서 수용 상태 r로 이동할 수 있다고 말한다.

PDA에 일반적으로 사용되는 표현은 없는 것 같습니다.여기서는 명령어$({\displaystyle p,}$ $a, A$${\displaystyle ,}$${\displaystyle }$q$,$$)$를 ${\displaystyle 상태}$ p에서 상태 ${\displaystyle q}$로${\displaystyle }$엣지$(\$$displaystyle$$a$$; A/\alpha$로 표시)($$읽기 a; 치환$$A를 α\$displaystyle \alpha$로 $표시{\displaystyle }$)$$로 나타냅니다.

계산 프로세스의 이해

다음으로 상기의 PDA가 다른 입력 문자열로 어떻게 계산되는지를 나타냅니다.스텝 기호 $「\displaystyle\vdash」$의 서브스크립트 M은 생략되어 있습니다.

PDA 및 컨텍스트프리 언어

모든 문맥 없는 문법은 동등한 비결정론적 푸시다운 오토마톤으로 변환될 수 있습니다.문법의 파생 과정은 가장 왼쪽에 있는 방식으로 시뮬레이션됩니다.문법에 의해 비터미널이 고쳐지는 경우 PDA는 최상위 비터미널을 스택에서 가져와 문법 규칙(확장)의 오른쪽 부분으로 대체합니다.문법이 터미널 기호를 생성하는 경우, PDA는 스택의 맨 위에 있는 기호(일치)일 때 입력에서 기호를 읽습니다.어떤 의미에서 PDA의 스택은 파생 트리의 사전 순서 트래버스에 대응하는 문법의 미처리 데이터를 포함한다.

기술적으로 문맥이 없는 문법이 주어졌을 때 PDA는 단일 상태 1을 가지며, 그 전이 관계는 다음과 같이 구성된다.

1. ${\displaystyle }$$각{\displaystyle }$ ${\displaystyle \mathrm{규칙}A}$ ${\displaystyle \to }$α ${\displaystyle \{\backslash }$$style$A${\displaystyle \backslash }$$to$\alpha $}$ (1 , \$varepsilon$ , A , 1 , \$alpha )$ (1$$ , \$displaystyle$ ( 1$,$ $\varepsilon$,$A , 1$, \alpha )$$） ${\displaystyle 。}$
2. ${\displaystyle (1}$, ${\displaystyle a}$, ${\displaystyle \mathrm{a}}$ , a${\displaystyle }$, ${\displaystyle 1}$ , ${\displaystyle )}$ ) $)(각$ 단말기의 {displaystyle $(1, a$, $a,$ 1, $\varepsilon$))는$,$ 「\$displaystyle$a}($$일치)」를 $나타냅니다{\displaystyle }$.

PDA는 빈 스택으로 받아들인다.첫 번째 스택 기호는 문법의 시작 ^{[citation needed]}기호입니다.

Greibach normal 형식의 문맥 없는 문법의 경우, 각 문법 규칙 A → a에 대해 (1,a,A)를 정의하면 동등한 비결정론적 푸쉬다운 ^{[2]: 115} 오토마톤도 생성된다.

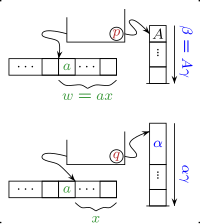
반대로 주어진 PDA에 대한 문법을 찾는 것은 쉽지 않습니다.요령은 PDA의 두 상태를 문법의 비말단으로 코드화하는 것이다.

정리.각 푸시다운 $오토마톤{\displaystyle }$M(\$displaystyle$ M$)$에 대해 N${\displaystyle (M)}$ $=$ $)$ {$displaystyle$ N$(M$)=$L(G$^{[2]: 116} 이 $되도록{\displaystyle }$ 문맥이 없는 $문법{\displaystyle }$G(\$displaystyle$G)를$$ 구성할 수 있습니다.

결정론적 푸시다운 오토마톤(DPDA)에 의해 받아들여지는 문자열의 언어를 결정론적 컨텍스트프리 언어라고 부릅니다.모든 문맥이 없는 언어가 결정론적인 ^{[note 1]}것은 아닙니다.그 결과, DPDA는 PDA의 완전히 약한 변형입니다.일반 언어에서도 크기가 폭발적으로 증가하는 문제가 있습니다.$재귀{\displaystyle }$ $함수{\displaystyle }$f\$displaystyle$f$$\$displaystyle$ n\$displaystyle$ n$\backslash$displaystyle n$\displaystyle$ n\displaystyle n$\$displaystyle n\$display$ style n}의 최소 DPDA가${\displaystyle }$^[4]f(\$displaystyle$ f$(n)$ $상태$를 갖는 정규 언어)를 나타냅니다$$.많은 비정규 PDA에서 동등한 DPDA는 무제한의 상태를 필요로 합니다.

2개의 스택에 액세스 할 수 있는 유한 오토마톤은 튜링 ^{[2]: 171} 머신과 동등한 파워의 디바이스입니다.선형유계오토마톤은 푸쉬다운오토마톤보다 강력하지만 ^{[note 2]}튜링기계보다는 덜 강력한 장치이다.

PDA 및 튜링 머신

푸쉬다운 오토마톤은 다음과 같이 2개의 테이프가 있는 '제한된' 튜링 머신(TM)과 계산상 동등합니다.첫 번째 테이프에서는 TM은 입력을 읽고 왼쪽에서 오른쪽으로만 이동할 수 있습니다(변경할 수 없습니다).두 번째 테이프에서는 데이터를 '푸시'하고 '팝'할 수만 있습니다.또는 각 단계에서 실행할 수 있는 유일한 조작은 문자열의 왼쪽 끝 문자(팝)를 삭제하거나 문자열의 왼쪽 끝 문자(푸시)에 왼쪽 문자를 추가하는 것(푸시) 중 하나뿐이라는 제약에 따라 읽기, 쓰기, 좌우로 이동할 수 있습니다.

PDA가 TM보다 약하다는 것은 '팝' 절차로 일부 데이터가 삭제된다는 것으로 요약할 수 있습니다.PDA를 TM만큼 강력한 PDA로 만들기 위해서는 '팝'을 통해 손실된 데이터를 어딘가에 저장해야 합니다.두 번째 스택을 도입함으로써 이를 달성할 수 있습니다.전항의 PDA의 TM 모델에서는, 이것은 3개의 테이프가 있는 TM에 상당합니다.첫 번째 테이프는 읽기 전용 입력 테이프이고, 두 번째와 세 번째 테이프는 '푸시 앤 팝'(스택)이러한 PDA가 임의의 TM을 시뮬레이트 하기 위해서, 양쪽의 스택을 비운 채로, 첫 번째 테이프에 PDA의 입력을 제공합니다.그런 다음 입력 테이프에서 첫 번째 스택으로 모든 입력을 푸시합니다.입력 전체가 첫 번째 스택으로 전송되면 일반 TM과 같이 진행됩니다.테이프상에서 오른쪽으로 이동하면 첫 번째 스택에서 심볼이 튀어나와 두 번째 스택에 (업데이트될 가능성이 있음) 심볼이 삽입되고 왼쪽으로 이동하면 두 번째 스택에서 심볼이 튀어나와 (업데이트될 가능성이 있음) 심볼이 삽입됩니다.첫 번째 스택따라서 모든 TM을 시뮬레이트할 수 있는 2개의 스택이 있는 PDA가 있습니다.

Generalized Pushdown Automaton(GPDA)

GPDA는 기존의 길이의 문자열 전체를 스택에 쓰거나 문자열 전체를 한 번에 스택에서 삭제하는 PDA입니다.

GPDA는 공식적으로 6-튜플로 정의된다.

${\displaystyle M=(Q,\Sigma,\Gamma,\gamma,\q_{0},\F)}$

$여기$서 Q${\displaystyle ,}$ ${\displaystyle \mathrm{\sigma },{}_{}}$, ${\displaystyle {q\mathrm{}}_{}}$ 0$(\$ Q$,\Sigma,\Gamma,,q_{0$ 및 $(\displaystyle$ F$)$는 PDA와 동일하게 정의됩니다.

${\$ { $displaystyle$} , \ $delta{\displaystyle }$$$}${\displaystyle }$: Q ×${\displaystyle {\mathrm{}}_{}}$ ×${\displaystyle {}^{\mathrm{}}q}$P ( ${\displaystyle {\mathrm{}}^{}}$×$display$ ) 。{ $display style Q$ \ $times$ \ $Sigma$_ { \ $epsilon }$ \ $times$ \ Gamma$^$ { * } \ $longrightarrow$P ( $Q$ \ $times$ \ Gamma $^$ * )

전환 함수입니다.

GPDA의 계산 규칙은 ${\displaystyle a_{}}$+ $(\$ $및{\displaystyle {}_{}}$ b${\displaystyle i_{}}$ + $(\$이 기호가 아닌 문자열이라는 점을 제외하고 PDA와 동일합니다.

GPDA와 PDA는 언어를 PDA로 인식하면 GPDA로 인식한다는 점에서 동등하다.

다음 시뮬레이션을 사용하여 GPDA와 PDA의 동등성에 대한 분석 증거를 작성할 수 있습니다.

(${\displaystyle {q\mathrm{}}_{}1}$, ${\displaystyle {}_{},}$ ${\displaystyle {}_{}{}_{}}$ 1 ${\displaystyle {x\mathrm{}}_{}}$ 2${\displaystyle {}_{}{}_{}}$ x${\displaystyle {}_{}{m}_{}}$ ) ${\displaystyle (}$ ( ${\displaystyle {q\mathrm{}}_{}}$ 2,${\displaystyle {}_{}{}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ y${\displaystyle }$2 .${\displaystyle }$. ${\displaystyle y_{}}$ n )$${ $display$ style $\delta$( $q$_ {1$}$ $,$ w , $x _ {$2$} \ cdot$ x _ { $m$} \ $long$ rightarrow ( $q _$ { 2 ,$y$ _ { 1 }$y$ _ { 2 . $2$} ) 。$y_{n}}$는 GPDA의 천이입니다.

$여기$서 ${\displaystyle {}_{}}$ 1,${\displaystyle {}_{}{q\mathrm{}}_{}}$ 2${\displaystyle q}$ ${\displaystyle Q}$, w ${\displaystyle \in }$ 、 ${\displaystyle {\sigma }_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {}_{}{}_{}{1\mathrm{}}_{}}$, x${\displaystyle {}_{}{2\mathrm{}}_{}}$,${\displaystyle \dots ,}$ ${\displaystyle x_{}}$ m${\displaystyle {}_{}{}^{}}$、 、 ${\displaystyle 0}$、 ${\displaystyle {}_{}{}_{}{}_{}}$,${\displaystyle \dots ,{}_{}{y}_{}}$ 2 、 …, ${\displaystyle y{}^{}}$n${\displaystyle {}^{}{}_{}}$ 0$$ 0 \ $display q_{1$}, $q_{2$}\$inQ, \in\sigma$ _ _ _ _ _ _ 。

PDA 에 대해서, 다음의 트랜지션을 설정합니다.

${\displaystyle{\begin{배열}{lcl}\delta '(q_{1},w,x_{1})&, \longrightarrow&(p_{1},\epsilon)\\\delta '(p_{1},\epsilon ,x_{2})&, \longrightarrow&(p_{2},\epsilon)\\&, \vdots &, \\\delta '(p_{m-1},\epsilon ,x_{m})&, \longrightarrow&(p_{m},\epsilon)\\\delta '(p_{m},\epsilon ,\epsilon)&, \longrightarrow&(p_{m+1},y_{n}.)\\\delta '(p_{m+1},\epsilon ,\epsilon)&\longrightarrow &(p_{m+2},y_{n-1})\\vdots &\longrightarrow &(p_{m+n-1},\ilon,\ilon)\longrightarrow &(q_{2},y_{1}).\end {array}}$

스택 오토마톤

푸시다운 오토마타의 일반화로서 Ginsburg, Greibach 및 Harrison(1967)은 스택 오토마타를 조사했습니다.스택 오토마타는 입력 문자열에서 왼쪽 또는 오른쪽으로 추가 스텝(슬립아웃을 방지하기 위해 특별한 엔드마커 기호로 둘러싸임)하여 스택 내에서 스텝 업 또는 다운할 수 있습니다.^[5][6]스택 오토마톤이 스택에서 팝업되지 않으면 비지우기라고 불립니다.비결정적, 비삭제적 스택오토마타에 의해 받아들여지는 언어의 클래스는 NSPACE(n²)입니다.NSPACE(n)는 상황에 맞는 ^[1]언어의 상위 집합입니다.결정론적 비삭제 스택오토마타가 받아들이는 언어 클래스는 DSPACE(n'log(n))^[1]입니다.

교체식 푸시다운 오토마타

APDA(Alternating Pushdown Automaton)는 상태가 설정된 푸시다운 자동화입니다.

• ${\displaystyle Q}$ ${\displaystyle =}$ ${\displaystyle {}_{}}$ $=$Q ∀∀$Q 、$ { \ $exists$} \ $cup$ Q _ { \ $for$ } $。$$여기$서 Q${\displaystyle {\mathrm{}}_{}}$、 ${\displaystyle {}_{}}$ ${\displaystyle {}_{}}$ \ $display style$ Q _ { \ $exists$} \ $cap Q$_ { \ $forall$ } = \ $emptyset$ $\}$ 。

Q$(\$ $및$ Q$(\$ $상태$는 존재론적 응답이라고 불립니다.보편적실존상태에서 APDA는 비결정적으로 다음 상태를 선택하고 결과 계산 중 적어도 하나가 받아들여지면 받아들인다.유니버설 상태에서는 APDA는 모든 다음 상태로 이동하고 모든 결과 계산이 허용되는지 여부를 승인합니다.

이 모델은 찬드라, 코젠, 스톡마이어에 ^[7]의해 소개되었다.Ladner, Lipton 및 Stockmeyer는^[8] 이 모델이 EXPTIME과 동등하다는 것을 증명했다. 즉, 지수 시간 알고리즘에 의해 결정될 수 있는 경우에만 일부 APDA에 의해 언어가 허용된다.

아이지코위츠와 카민스키는^[9] 비결정론적 PDA와 같은 방식으로 결합문법에 해당하는 동기식 교대 푸시다운 오토마타(SAPDA)를 도입했다.

「 」를 참조해 주세요.

• 스택 머신
• 문맥 자유 문법
• 유한 오토마톤
• 카운터 오토마톤
• 큐오토마톤

메모들

레퍼런스

• Michael Sipser (1997). Introduction to the Theory of Computation. PWS Publishing. ISBN 0-534-94728-X. 섹션 2.2: 푸시다운 오토마타, 페이지 101–114.
• Jean-Michel Autebert, Jean Berstel, Luc Boasson, Context-Free Languages and Push-Down Automata, in: G. Rozenberg, A. Saloma(에드), 정식언어 핸드북, Vol.1, Springer-Verlag, 1997-174.

외부 링크

• JFLAP, 비결정적 푸시다운 오토마타를 포함한 여러 유형의 오토마타를 위한 시뮬레이터
• CoAn, 비결정적 푸시다운 오토마타(C++, Windows, Linux, MacOS)를 포함한 여러 종류의 머신에 대한 또 다른 시뮬레이터