재귀 최소 제곱 필터

재귀 최소 제곱(RLS)은 입력 신호와 관련된 가중 선형 최소 제곱 비용 함수를 최소화하는 계수를 재귀적으로 찾는 적응형 필터 알고리즘이다. 이 접근법은 평균 제곱 오차를 줄이는 것을 목표로 하는 최소 평균 제곱(LMS)과 같은 다른 알고리즘과 대조적이다. RLS의 도출에서 입력 신호는 결정론적인 것으로 간주되는 반면, LMS 및 유사한 알고리즘의 경우 그것들은 확률론적인 것으로 간주된다. RLS는 대부분의 경쟁사와 비교했을 때 매우 빠른 컨버전스를 보인다. 그러나 이러한 이점은 높은 계산 복잡성의 비용으로 발생한다.

동기

RLS는 가우스에 의해 발견되었지만 Plackett이 1821년부터 가우스의 원작을 재발견한 1950년까지 사용되지 않거나 무시되었다. 일반적으로 RLS는 적응형 필터로 해결할 수 있는 모든 문제를 해결하는 데 사용될 수 있다. 예를 들어, 신호 $d{\displaystyle (n}$) ${\displaystyle d(n)}$이(가) 에코이(가)를 통해 전송되어$$ 신호 d(n)가 다음과 같이 수신되도록 한다고 가정해 보십시오.

${\displaystyle x(n)=\sum _{k=0}^{qb_{n}(k)d(n-k)+v(n)}$

여기서 $v{\displaystyle }$(${\displaystyle n}$) ${\displaystyle v(n)}$은(는) 가법 노이즈를 나타낸다$$. RLS 필터의 목적은$$$p{\displaystyle }$+ ${\displaystyle 1}$ ${\displaystyle p+1}$-tap$$ FIR 필터, w ${\$을(를) 사용하여$$ 원하는 신호 $d{\displaystyle (n}$) ${\displaystyle$d$(n)}$을(를) 복구하는 것이다.

${\displaystyle d(n)\ 관련 \sum _{k=0}^{p}w(k)x(n-k)=\mathbf {w}^{\mathit{T}\mathbf {x} _{n}}}}}$

여기서 $x{\displaystyle {\mathbf{}}_{}}$ ${\displaystyle {}_{}}$=${\displaystyle }$[${\displaystyle }$( ${\displaystyle n}$) x${\displaystyle }$( ${\displaystyle \mathrm{n}}$- 1${\displaystyle }$)${\displaystyle }$… x${\displaystyle }$( ${\displaystyle n}$- ${\displaystyle p}$) ${\displaystyle {}^{}}$ ${\displaystyle T^{}}$ ${\$ \quadots $\quad x(n-p)]^$${T}$은${\displaystyle (}$는$)$ p${\displaystyle }$+ ${\displaystyle 1}$ {\$displaystyle p+1}$의 가장 $최근$ x ($){\displaystyle x(n)}$ 샘플을 포함하는 열 벡터 입니다$.$ 복구된 원하는 신호의 추정치는 다음과 같다.

${\dyplaystyle {\d}(n)=\sum _{k=0}^{p}w_{n}x(k)x(n-k)=\mathbf {w}_{n}^{n}{n}^{n}^{\mathbf{T}_{n}}}}}}}}}}}*mathbf {n}$

목표는 필터 $w{\displaystyle \mathbf{}}$ ${\${n$}$의 파라미터를 추정하는 것이며, $매번$$$ ${\displaystyle {}_{}}$$${\$displaystyle \$${\displaystyle {\}\}\},}_{}}$ ${\displaystyle {\mathrm{w}}_{}}$ +$$1 {\$displaystyle$ \$mathbf {w}$$_{n$+1}에 ${\displaystyle {}_{}}$적응된 $최소$ 제곱 추정치를 $참조$한다.$레이스타일 \mathbf{w} _{n}$ 역시 아래와 같이 컬럼 벡터로서$$, 전치(transpose)인 w {${\displaystyle {\mathit{}}_{}^{}}$ ${\$는 행 벡터다. The matrix product ${\displaystyle \mathbf {w} _{n}^{\mathit {T}}\mathbf {x} _{n}}$ (which is the dot product of ${\displaystyle \mathbf {w} _{n}}$ and ${\displaystyle \mathbf {x} _{n}}$) is ${\displaystyle {\hat {d}}(n)}$, a scalar. d ${\displaystyle \stackrel{}{^}}$( ${\displaystyle n}$)${\displaystyle }$- ${\displaystyle d}$( n${\displaystyle }$) ${\displaystyle {\d}(n)-d(n)}$이(가) 일부 최소 제곱 의미에서 크기가 작을$$ 경우 추정치는 "좋음"이다.

$시간$이 진화할수록 ${\displaystyle {\mathrm{w}}_{}}$ ${\displaystyle {}_{}}$${\displaystyle {}_{}}$+$$1 ${\$$displaystyle \mathbf$ {$w} _$${n$$+$$1}$에 대한 새로운 추정치를 찾기 위해 최소 제곱 알고리즘을 완전히 다시 수행하지 않는 것이 바람직하다$.$

RLS 알고리즘의 이점은 행렬을 반전시킬 필요가 없기 때문에 계산 비용을 절감할 수 있다는 것이다. 칼만 필터와 같은 결과 이면에 직관력을 제공한다는 점도 장점이다.

토론

RLS 필터의 이면에 있는 아이디어는 새 데이터가 도착하면 필터를 ${\displaystyle {}_{}}$하고$$n {\$displaystyle \mathbf$${w}$ _{$n}$의 필터 계수를 적절하게 선택하여$$ 비용 함수 $C{\displaystyle }$ {\$displaystyle C}$를 최소화하는 것이다. 오류 신호 $e{\displaystyle (n}$) ${\displaystyle e(n)}$ 및$$ 원하는 신호 $d{\displaystyle (n)}$ ${\displaystyle d(n)}$은(는) 아래의 음의 피드백 다이어그램에서 정의된다$$.

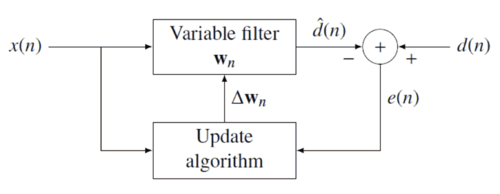
오류는 ${\displaystyle \mathrm{암묵적}}$으로 추정 $d{\displaystyle \stackrel{}{}}$ ${\displaystyle \stackrel{}{^}}$( n${\displaystyle }$) ${\displaystyle {\d}(n)}$을(를) 통한 필터 계수에 따라 달라진다$.$

${\displaystyle e(n)=d(n)-{\hat {d}(n)}$

따라서 가중 최소 제곱 오차 $함수{\displaystyle }$ C$${\$displaystyle C$ - 최소화하고자 하는 비용 함수 -${\displaystyle }e{\displaystyle }$ (${\displaystyle n}$ )$${\$displaystyle$ e$(n)}$의 함수도 필터 계수에 따라 달라진다$$.

${\displaystyle C(\mathbf {w} _{n}=\sum _{i=0}^{n}}\lambda ^{n-i}e^{2}(i)}$

여기서 < {\$displaystyle$0<\$displayda \leq 1}$은 오래된 오류 샘플에 기하급수적으로 적은 가중치를 주는 "변수 인자"이다.

${\displaystyle {}_{}}$ 벡터 $w{\displaystyle {\mathbf{}}_{}}$ ${\$의 모든 항목 $k{\displaystyle }$ ${\displaystyle k}$에 대한 부분파생상품을 취하고 결과를$$ 0으로 설정하여 비용함수를 최소화한다.

${\displaystyle {\frac {\partial C(\mathbf {w} _{n})}{\partial w_{n}(k)}}=\sum _{i=0}^{n}\,2\lambda ^{n-i}e(i)\,{\frac {\partial e(i)}{\partial w_{n}(k)}}={-}\sum _{i=0}^{n}\,2\lambda ^{n-i}e(i)\,x(i-k)=0\qquad k=0,1,\cdots ,p}$

다음으로 e (${\displaystyle n}$) ${\displaystyle e(n)}$을(를) 오류 신호의 정의로 대체하십시오$$.

${\displaystyle \sum \sum \{i=0}^{n-i}\왼쪽[d(i)-\sum _{l=0}w_{n}x(i-l)\right]x(i-k)=0\qquad k=0,1,\cdots,p}$

방정식 산출물 재배열

${\displaystyle \sum _{l=0}^{p}w_{n}(l)\left[\sum _{i=0}^{n}\lambda ^{n-i}\,x(i-l)x(i-k)\right]=\sum _{i=0}^{n}\lambda ^{n-i}d(i)x(i-k)\qquad k=0,1,\cdots ,p}$

이 형식은 행렬 단위로 표현할 수 있다.

${\dplaystyle \mathbf {R} _{x}(n)\,\mathbf {w} _{n}=\mathbf {r} _{dx}(n)}$

where ${\displaystyle \mathbf {R} _{x}(n)}$ is the weighted sample covariance matrix for ${\displaystyle x(n)}$, and ${\displaystyle \mathbf {r} _{dx}(n)}$ is the equivalent estimate for the cross-covariance between ${\displaystyle d(n)}$ and ${\displaystyle x(n)$$\}\}$ 이 식을 바탕으로 비용 함수를 최소화하는 계수를 다음과 같이 찾아낸다.

${\displaystyle \mathbf {w} _{n}=\mathbf {R} _{x}^{-1(n)\,\mathbf {r} _{dx}(n)}$

이것이 토론의 주된 결과다.

λ 선택

$\lambda {\displaystyle }$ ${\displaystyle \lambda }$이(가) 작을수록 공분산 행렬에 대한 이전 표본의 기여도가 작다. 이는 필터가 최근 샘플에 더 민감하게 반응하게 만들며, 이는 필터 공효과의 변동이 더 크다는 것을 의미한다. $\lambda {\displaystyle }$= ${\displaystyle 1}$ ${\displaystyle \lambda =1}$ 케이스는$$ 성장하는 윈도우 RLS 알고리즘으로 불린다. 실제로 $\lambda {\displaystyle }$ ${\displaystyle \lambda }$은(는) 대개 0.98과 1 사이에서 선택된다$$.^[1] 타입 II 최대우도 추정을 사용하면 데이터 집합에서 최적 ${\displaystyle \lambda }$을(를) 추정할 수 있다$$.^[2]

재귀 알고리즘

논의 결과 비용 함수를 최소화하는 계수 벡터를 결정하기 위한 단일 방정식이 도출되었다. 이 섹션에서는 양식의 재귀적 솔루션을 도출하고자 한다.

${\displaystyle \mathbf {w} _{n}=\mathbf {w} _{n-1}+\Delta \mathbf {w} _{n-1}$

where ${\displaystyle \Delta \mathbf {w} _{n-1}}$ is a correction factor at time ${\displaystyle {n-1}}$. We start the derivation of the recursive algorithm by expressing the cross covariance ${\displaystyle \mathbf {r} _{dx}(n)}$ in terms of ${\displaystyle \mat$$hbf {r} _{dx}(n-1)}$

${\displaystyle \mathbf {r} _{dx}(n)}$	${\displaystyle =\sum _{i=0}^{n}\\da ^{n-i}d(i)\mathbf {x}(i)}$
	${\displaystyle =\sum _{i=0}^{n-1}\mathda ^{n-i}d(i)\mathbf {x}(i)+\mathda ^{0d(n)\mathbf {x}(n)}$
	${\displaystyle =\mathbf {r} _{dx}(n-1)+d(n)\mathbf {x}(n)}$

여기서 $x{\displaystyle \mathbf{}}$( ${\displaystyle i}$) ${\displaystyle \mathbf {x}(i)}$은(는) $p{\displaystyle }$+ ${\displaystyle 1}$ ${\$ 치수$$ 데이터 벡터임

${\displaystyle \mathbf {x}(i)=[x(i),x(i-1),\reason,x(i-p)]^{T}$

마찬가지로 $우리$는 R ${\displaystyle {}_{}}$(${\displaystyle }$n ) ${\displaystyle \mathbf {R} _{x}(n)$을 R ${\displaystyle {}_{}}$(${\displaystyle \mathrm{n}}$ ${\displaystyle -}$ 1${\displaystyle }$)$${\$displaystyle \mathbf {R} _{x}(n-1$) 단위로 표현한다.

${\displaystyle \mathbf {R} _{x}(n)}$	${\displaystyle =\sum _{i=0}^{n}\lambda ^{n-i}\mathbf {x}(i)\mathbf {x}^{T}(i)}$
	${\displaystyle =\lambda \mathbf {R} _{x}(n-1)+\mathbf {x}(n)\mathbf {x}^{T}(n)}$

계수 벡터를 생성하기 위해 결정론적 자동 공분산 행렬의 역행렬에 관심이 있다. 그 일에는 우드베리 매트릭스 정체성이 유용하다. 와 함께

$(\displaystyle A}$	${\displaystyle =}$ ${\displaystyle \lambda }$ ${\displaystyle {\mathbf{}}_{}}$ ${\displaystyle {}_{}}$( ${\displaystyle \mathrm{n}}$- ${\displaystyle 1}$) ${\displaystyle =\lambda \mathbf {R} _{x}(n-1$)는${\displaystyle }$(${\displaystyle p}$+ ${\displaystyle 1}$) ${\displaystyle (p+1)$-by-$$${\displaystyle p}$+ ${\displaystyle 1}$) ${\displaystystyle (p+1$)}이다$.$
$U}$	${\displaystyle =}$ ${\displaystyle x\mathbf{}}$( ${\displaystyle n}$) ${\displaystyle =\mathbf {x}(n)}$은$({\displaystyle }$는) (${\displaystyle p}$+ ${\displaystyle 1}$) ${\displaystyle (p+1)$-by-1$$(열 벡터)
$(\displaystyle V}$	${\displaystyle =}$ ${\displaystyle {\mathbf{}}^{}}$ ${\displaystyle {}^{}n}$ ${\displaystyle )}$ ${\displaystyle =\mathbf {x} ^{T}(n)}$은(는) 1-by${\displaystyle p}$+ ${\displaystyle 1}$) ${\displaystyle(p+1)}($행 벡터)
$(\displaystyle C)$	${\displaystyle =}$ ${\displaystyle {\mathbf{}}_{}}$ ${\displaystyle {\mathrm{}}_{}}$ ${\$}는$$ 1-by-1 ID 행렬이다.

우드베리 매트릭스 정체성은 다음과 같다.

${\displaystyle \mathbf {R} _{x}^{-1}(n)}$	${\displaystyle =}$	${\displaystyle \left[\lambda \mathbf {R} _{x}(n)+\mathbf {x}(n) ^{T}(n)\right]^{-1}$
	${\displaystyle =}$	${\displaystyle \lambda ^{-1}\mathbf {R} _{x}^{-1}(n-1)}$
		${\displaystyle -\lambda ^{-1}\mathbf {R} _{x}^{-1(n-1)\mathbf {x}(n)}$
		${\displaystyle \left\{1+\mathbf {x} ^{T}(n)\lambda ^{-1}\mathbf {R} _{x}^{-1}(n-1)\mathbf {x} (n)\right\}^{-1}\mathbf {x} ^{T}(n)\lambda ^{-1}\mathbf {R} _{x}^{-1}(n-1)}$

표준 문헌에 부합하기 위해, 우리는 정의한다.

${\displaystyle \mathbf {P}(n)}$	${\displaystyle =\mathbf {R} _{x}^{-1}(n)}$
	${\displaystyle =\lambda ^{-1}\mathbf {P}(n-1)-\mathbf {g}(n)\mathbf {x}^{T}(n)\lambda ^{-1}\mathbf {P}(n-1)}$

여기서 게인 벡터 $g{\displaystyle (n}$) ${\displaystyle g(n)}$은(는)

${\displaystyle \mathbf {g}(n)}$	${\displaystyle =\lambda ^{-1}\mathbf {P}(n-1)\mathbf {x}\n)\mathbf {x}{1+\mathbf {x}^{T}(n-1)\mathbf {x}\right\1}{1}-1}{1}-1}:{1}-1}:{1}-1}*mathb^-1}:{1}-}-}-1}$
	${\displaystyle =\mathbf {P}(n-1)\mathbf {x}(왼쪽)\{\lambda +\mathbf {x}^{T}(n-1)\mathbf {x}(n)\right\}^{-1}:{-1}$

다음 단계로 ${\displaystyle \mathrm{넘어가기}}$ 전에 g${\displaystyle }$(n$$) {\$displaystyle \mathbf$ {$g}($n)}을(를) 다른 형태로$$ 가져와야 한다$.$

${\displaystyle \mathbf {g}\좌측\{1+\mathbf {x}^{T}(n)\lambda^{-1}\mathbf {P}(n-1)\mathbf {x}\오른쪽\}}}}$	${\displaystyle =\lambda ^{-1}\mathbf {P}(n-1)\mathbf {x}(n)}$
${\displaystyle \mathbf {g}+\mathbf {g}(n)\mathbf {x}^{T}(n)\lambda ^{-1}\mathbf {P}(n-1)\mathbf {x}(n)}$	${\displaystyle =\lambda ^{-1}\mathbf {P}(n-1)\mathbf {x}(n)}$

왼쪽에서 두 번째 항을 뺀 값

${\displaystyle \mathbf {g}(n)}$	${\displaystyle =\lambda ^{-1}\mathbf {P}(n-1)\mathbf {x}-\mathbf {g}(n)-\mathbf {x}^{T}(n)\lambda ^{-1}\mathb {P}\mathb {xf {x}(n)}}$
	${\displaystyle =\lambda ^{-1}\왼쪽[\mathbf {P}-\mathbf {g}(n)\mathbf {x}^{T}(n)\mathbf {P}(n-1)\right]\mathbf {x}(n)}$

$P{\displaystyle \mathbf{}(n}$) ${\displaystyle \mathbf {P}(n)}$의 재귀적 정의에서 원하는$$ 형식이 다음과 같다.

${\displaystyle \mathbf {g}(n)=\mathbf {P}(n)\mathbf {x}(n)}$

이제 우리는 재발을 완료할 준비가 되었다. 논의한 바와 같이

${\displaystyle \mathbf {w} _{n}}$	${\displaystyle =\mathbf {P}(n)\,\mathbf {r} _{dx}(n)}$
	${\displaystyle =\lambda \mathbf {P}(n)\\mathbf {r} _{dx}(n-1)+d(n)\mathbf {P}\mathbf {x}(n)}$

두 번째 단계는 $r{\displaystyle {\mathbf{}}_{}}$ ${\displaystyle d_{}}$ ${\displaystyle {}_{}}$( n${\displaystyle }$) ${\displaystyle \mathbf {r} _{dx}(n)}$의 재귀적 정의에서 따옴$.$ 다음은 P ${\displaystyle (n}$ ${\displaystyle )}$ ${\$$displaysty \mathbf {P$$}$의 대체 형태와 $함께{\displaystyle \mathbf{}}$ p$$ ($n{\displaystyle \mathbf{}}$)의 재귀적 정의를 통합하고 g $)$를 얻는다.

${\displaystyle \mathbf {w} _{n}}$	${\displaystyle =\lambda \left[\lambda ^{-1}\mathbf {P} (n-1)-\mathbf {g} (n)\mathbf {x} ^{T}(n)\lambda ^{-1}\mathbf {P} (n-1)\right]\mathbf {r} _{dx}(n-1)+d(n)\mathbf {g} (n)}$
	${\displaystyle =\mathbf {P} (n-1)\mathbf {r} _{dx}(n-1)-\mathbf {g} (n)\mathbf {x} ^{T}(n)\mathbf {P} (n-1)\mathbf {r} _{dx}(n-1)+d(n)\mathbf {g} (n)}$
	${\displaystyle =\mathbf {P} (n-1)\mathbf {r} _{dx}(n-1)+\mathbf {g} (n)\left[d(n)-\mathbf {x} ^{T}(n)\mathbf {P} (n-1)\mathbf {r} _{dx}(n-1)\right]}$

${\displaystyle {}_{}}$ -${\displaystyle 1_{}}$= ${\displaystyle P\mathbf{}}$ (${\displaystyle }$n${\displaystyle }$- ${\displaystyle 1}$) r ${\displaystyle {}_{}}$ (${\displaystyle {}_{}{n}_{}}$- ${\displaystyle 1}$ )${\displaystyle \mathbf {w} _{n-1}=\mathbf {P}(n-1)\mathbf {$r$} _{dx}($n-1)을$$사용하여 업데이트$$ 방정식에 도달한다.

${\displaystyle \mathbf {w} _{n}}$	${\displaystyle =\mathbf {w} _{n-1}+\mathbf {g}(n)\왼쪽[d(n)-\mathbf {x}^{T}(n)\mathbf {w} _{n-1}\right]}$
	${\displaystyle =\mathbf {w} _{n-1}+\mathbf {g}(n)\mathbf(n)}$

여기서 $\alpha {\displaystyle }$( ${\displaystyle n}$)${\displaystyle }$= ${\displaystyle d}$(${\displaystyle }$n )${\displaystyle }$- ${\displaystyle {\mathbf{}}^{}}$ T${\displaystyle {}^{}}$(${\displaystyle n}$ ${\displaystyle )}$ ${\displaystyle {}_{}}$- ${\displaystyle 1_{}}$ $(\$는 선행 오류다. 후미 오류와 비교하십시오. 필터가 업데이트된 후 계산된 오류:

${\displaystyle e(n)=d(n)-\mathbf {x}^{T}(n)\mathbf {w} _{n}}$

그 말은 우리가 보정 계수를 찾았다는 겁니다.

${\displaystyle \Delta \mathbf {w} _{n-1}=\mathbf {g}(n)\alpha(n)}$

이러한 직관적인 만족도 결과는 보정 계수가 가중 인자 $,{\displaystyle \lambda }$를 통해 원하는 감도를 제어하는 오차와 게인 벡터 모두에 정비례한다는 것을 나타낸다$.$

RLS 알고리즘 요약

p-th 순서 RLS 필터에 대한 RLS 알고리즘은 다음과 같이 요약할 수 있다.

매개 변수:	${\displaystyle p}$= ${\displaystyle$ p$=}$필터$$ 순서
	${\displaystyle \lambda }$= ${\displaystyle \lambda =}$잊는$$ 요인
	${\displaystyle \Delta }$= ${\displaystyle \delta =}$ 값을$$ 초기화하여 $P{\displaystyle \mathbf{}}$(${\displaystyle 0}$) ${\displaystyle \mathbf {P} (0)}$
초기화:	${\displaystyle \mathbf{w}}$( ${\displaystyle n}$)${\displaystyle }$= ${\displaystyle 0}$ ${\displaystyle \mathbf {w}(n)=0$
	${\displaystyle x}$( ${\displaystyle k}$)${\displaystyle }$= ${\displaystyle 0,}$ ${\displaystyle k}$=${\displaystyle }$- p${\displaystyle }$,${\displaystyle }$…${\displaystyle }$,${\displaystyle }$- ${\displaystyle 1}$ ${\displaystyle x(k)=0,k=-p,\cHB,-1$
	${\displaystyle d(k)=0,k=-p,\filename ,-1}$
	${\displaystyle }$$P{\displaystyle }$${\displaystyle }$( ${\displaystyle 0}$)${\displaystyle }$= ${\displaystyle \Delta }$ ${\displaystyle I}$ ${\displaystyle \mathbf {P} (0)=\delta I}$ 여기서$$ I ${\$$displaystyle$ $I$$}$은 순위 p + $1$의$ID$ ${\displaystyle \mathrm{행렬}}$이다$.$
계산:	$n{\displaystyle }$= ${\displaystyle 1}$,${\displaystyle 2}$,${\displaystyle }$…의 경우, ${\displaystyle n=1,2,\dots }$
	${\displaystyle \mathbf {x}(n)=\left[{\put}x(n)\x(n-1)\\\vdots \\x(n-p)\end{nd}\right]}}$
	${\displaystyle \alpha(n)=d(n)-\mathbf {x}^{T}(n)\mathbf {w}(n-1)}$
	${\displaystyle \mathbf {g}(n)=\mathbf {P}(n-1)\mathbf {x}(n)\lambda +\mathbf {x}^{T}(n-1)\mathbf {x}(n)\mathbf {x}{-1}^{-1}}}}}}}:{-1}}}}}}}}}}}}}}}}}}}}}}}}:{-1}$
	${\displaystyle \mathbf {P}(n)=\lambda ^{-1}-\mathbf {g}-\mathbf {g}(n)-\mathbf {x}^{T}(n)\lambda ^{-1}\mathbf {P}(n-1)}$
	${\displaystyle w\mathbf{}}$( ${\displaystyle n}$)${\displaystyle }$= w${\displaystyle }$( ${\displaystyle \mathrm{n}}$- ${\displaystyle 1}$)${\displaystyle }$+ ${\displaystyle \alpha \mathbf{}}$( n${\displaystyle }$) g ${\displaystyle (n}$) ${\displaystyle \mathbf {w}(n)=\mathbf {w}(n-1)+\\\n)\mathbf$ {$g}(n$

$P{\displaystyle }$ ${\displaystyle P}$에 대한 재귀는 대수 리카티 방정식을 따르며$$ 따라서 Kalman 필터와 평행선을 그린다.^[3]

격자 재귀 최소 제곱 필터(LRLS)

Lattice Recursive Lest Square 적응 필터는 산술 연산(순서 N)이 적게 필요하다는 점을 제외하고 표준 RLS와 관련이 있다.^[4] 기존 LMS 알고리즘보다 빠른 수렴율, 모듈형 구조, 입력상관 매트릭스의 고유값 스프레드 변화에 대한 불감증 등 추가적인 장점을 제공한다. 기술된 LRLS 알고리즘은 사후 오류에 기초하며 정규화된 형태를 포함한다. The derivation is similar to the standard RLS algorithm and is based on the definition of ${\displaystyle d(k)\,\!}$. In the forward prediction case, we have ${\displaystyle d(k)=x(k)\,\!}$ with the input signal ${\displaystyle x(k-1)\,\!}$ as the most up to date sample. 후진 예측 사례는 $d{\displaystyle }$( ${\displaystyle k}$)${\displaystyle }$= ${\displaystyle x}$( ${\displaystyle k}$- ${\displaystyle \mathrm{i}}$- 1${\displaystyle }$) $displaystyle d(k)=x(k-i-1)\,\!}$이며$,$ 여기서 나는 우리가 예측하고자 하는 과거의 표본의 지수이고, 입력 신호 $x{\displaystyle }$ ${\displaystyle (k}$ ${\displaystyle )}$ $displaystysty x(k)\,\!}$은 가장 최근의 표본이다.^[5]

매개 변수 요약

${\displaystyle {\kappa }_{}}$ ${\displaystyle f_{}}$( ${\displaystyle k}$, ${\displaystyle i}$) $displaystyle \kappa _{f}(k,i)\,\!}$은(는) 전방반사 계수임

${\displaystyle {\kappa }_{}}$ ${\displaystyle b_{}}$( k${\displaystyle }$, ${\displaystyle i}$) $displaystyle \kappa _{b}(k,i)\,\!}$은(는) 역반사 계수다.

${\displaystyle e_{}}$ ${\displaystyle f_{}}$( ${\displaystyle k}$, ${\displaystyle i}$) $displaystyle e_{f}(k,i)\,\!}$은(는) 후방의 전방 예측 오류를 나타낸다$$.

${\displaystyle e_{}}$ ${\displaystyle b_{}}$( ${\displaystyle k}$, ${\displaystyle i}$) $displaystyle e_{b}(k,i)\,\!}$은(는) 후방의 역방향 예측 오류를 나타낸다$$.

${\displaystyle {\xi }_{}^{}}$ ${\displaystyle {b{}_{}}_{}^{}}$ ${\displaystyle {m_{}}_{}^{}}$ ${\displaystyle {{\mathrm{in}}_{}}_{}^{}}$ ${\displaystyle {{}_{}}_{}^{}}$( ${\displaystyle k}$, i${\displaystyle }$) $displaystyle \xi _{b_}^{d}(k,i)\,\!}$은(는) 최소 최소값 후진 예측 오류임

${\displaystyle {\xi }_{}^{}}$ ${\displaystyle {f{}_{}}_{}^{}}$ m ${\displaystyle {i_{}}_{}^{}}$ ${\displaystyle {n_{}}_{}^{}}$ ${\displaystyle {{}_{}}_{}^{}}$( ${\displaystyle k}$, ${\displaystyle i}$) $displaystyle \xi _{f_}^{d}(k,i)\,\!}$은(는) 최소 최소 최소값 전방 예측 오류임

${\displaystyle \gamma }$(${\displaystyle k}$, ${\displaystyle i}$) $displaystyle \gamma(k,i)\,\!}$은(는) priori 오류와 properi 오류 사이의 변환 계수다$$.

${\displaystyle v_{}}$ ${\displaystyle i_{}}$( ${\displaystyle k}$) $displaystyle v_{i}(k)\,\!}$은(는) 피드포워드 승수 계수다.

${\displaystyle ϵ}$ $displaystyle \epsilon \,\!}$은(는) 0.01일 수 있는 작은 양의 상수임

LRLS 알고리즘 요약

LRLS 필터 알고리즘은 다음과 같이 요약할 수 있다.

초기화:
	i = 0,1,...,N의 경우
	${\displaystyle \Delta (}$- ${\displaystyle 1}$,${\displaystyle i}$)${\displaystyle }$= ${\displaystyle {}_{}}$ ${\displaystyle D_{}}$- ${\displaystyle 1}$,${\displaystyle i}$)${\displaystyle }$= ${\displaystyle 0}$ $displaystyle \delta(-1,i)=\delta _{D}(-1,i)=0\,\!}($k < 0의 경우 x(k) = 0))
	${\displaystyle \xi _{b_{min}^{d}(-1,i)=\xi _{f_{min}^{d}(-1,i)=\엡실론}}$
	$\displaystyle \property(-1,i)=1\,\!}$
	${\displaystyle e_{b}(-1,i)=0\,\!}$
	끝
계산:
	k ≥ 0의 경우
	$\displaystyle \cHB(k,0)=1\,\!}$
	${\displaystyle e_{b}(k,0)=e_{f}(k,0)=x(k)\,\!}$
	${\displaystyle \xi_{b_{min}^{d}(k,0)=\x^{d}(k,0)=x^{2}(k)+\xi \f_}^{d}(k-1,0)\,\!}$
	${\displaystyle e(k,0)=d(k)\,\!}$
	i = 0,1,...,N의 경우
	${\displaystyle \property(k,i)=\frac(k-1,i)+{\frac {e_{b}(k-1,i)e_{f}{\property(k-1,i)}}{\i(k-1,i)}}}}}}}}}$
	${\displaystyle \cHB(k,i+1)=\i(k,i)-{\frac {e_{b}^{2}(k,i)}{\xi _{b_}^{d}(k,i)}}}}}}$
	${\displaystyle \kappa _{b}(k,i)={\frac {\frac(k,i)}{\xi_{f_{min}^{d}(k,i)}}}}}}$
	${\displaystyle \kappa _{f}(k,i)={\frac {\frac(k,i)}{\xi_{b_{min}^{d}(k-1,i)}}}}}}}$
	${\displaystyle e_{b}(k,i+1)=e_{b}(k-1,i)-\kappa_{b}(k,i)_{f}(k,i)\,\!}$
	${\displaystyle e_{f}(k,i+1)=e_{f}(k,i)-\appa_{f}(k,i)_{b}(k-1,i)\,\!}$
	${\displaystyle \xi _{b_{min}^{d}(k,i+1)=\xi _{b_{min}^{d}(k-1,i)-\capa _{b}(k,i)}$
	${\displaystyle \xi _{f_{min}^{d}(k,i+1)=\xi _{f_{min}^{d}(k,i)-\cappa _{f}(k,i)}$
	피드포워드 필터링
	${\displaystyle \delta _{D}(k,i)=\lambda \delta _{D}(k-1,i)+{\frac {e(k,i)_{b}{\gamma(k,i)}}}{\gamma(k,i)}}}}}}}}}}}}}}}:}$
	${\displaystyle v_{i}(k)={\frac {\delta _{D}(k,i)}{\xi _{b_{min}^{d}(k,i)}}}}}}$
	${\displaystyle e(k,i+1)=e(k,i)-v_{i}(k)e_{b}(k,i)\,\!}$
	끝
	끝

정규화된 격자 재귀 최소 제곱 필터(NLRLS)

LRLS의 정규화된 형태는 재귀와 변수가 적다. 알고리즘의 내부 변수에 정규화를 적용하여 크기를 1로 제한하여 유지할 수 있다. 이는 일반적으로 높은 계산 부하를 수반하는 분할 및 제곱근 연산의 수 때문에 실시간 애플리케이션에서는 사용되지 않는다.

NLRLS 알고리즘 요약

NLRLS 필터에 대한 알고리즘은 다음과 같이 요약할 수 있다.

초기화:
	i = 0,1,...,N의 경우
	${\displaystyle \stackrel{\text{'}}{\Delta }}$(${\displaystyle }$- ${\displaystyle 1}$,${\displaystyle i}$)${\displaystyle }$= ${\displaystyle 0}$ $displaystyle {\$displaystyle {\$overline{\\\(1,i)=0\,\}($만약 x($$k) = d(k) = 0(k) = k < 0)))
	${\displaystyle {\delta }_{D}(-1,i)=0\,\!}$
	${\displaystyle {\overline{e}_{b}(-1,i)=0\,\!}$
	끝
	${\displaystyle \ex}^{x}^{2}(-1)=\dda \ \ma_{d}^{2}(-1)=\epsilon \,\!}$
계산:
	k ≥ 0의 경우
	${\displaystyle {}_{}^{}\sigma }$ ${\displaystyle x_{}^{}}$ ${\displaystyle {}_{}^{}}$( k${\displaystyle }$)${\displaystyle }$= ${\displaystyle {}_{}^{}}$ ${\displaystyle x_{}^{}}$ ${\displaystyle {}_{}^{}}$( ${\displaystyle \mathrm{k}}$- ${\displaystyle 1}$)${\displaystyle }$+ ${\displaystyle {x\mathrm{}}^{}}$ ${\displaystyle 2}$ (${\displaystyle {}^{}}$k${\displaystyle }$) $displaystyle \sigma _{x}^{2}(k)=\lambda \sigma \{x}^{x$}($k-1)+x^{2(k)\,\}($입력 신호 에너지)
	${\displaystyle {\sigma }_{}^{}}$ ${\displaystyle d_{}^{}}$ ${\displaystyle {}_{}^{}}$(${\displaystyle k}$) = ${\displaystyle d_{}^{}}$ d ${\displaystyle {}_{}^{}}$(${\displaystyle }$k -${\displaystyle 1}$) + ${\displaystyle {d\mathrm{}}^{}}$ 2 ( )$디스플레이$ 스타일 $\sigma$ \sigma $_{d}^{2}(k)=\lambda \sigma \{d}^{d$}($k-1)+d^{2(k)\!}($참조 신호 에너지)
	${\displaystyle {{e}_{b}(k,0)={\overline{e}_{f}(k,0)={\frac {x(k)}{\x}}}}{x}(k)\!}$
	${\displaystyle {\overline{e}(k,0)={\frac {d(k)}{\d(k)}}{\d(k)}}\,\!}$
	i = 0,1,...,N의 경우
	${\displaystyle {\overline {\cHB}{b}^{2}{1-{\overline{e}_{b}^{ni) (1-{\overline{e}_{f}^{2}(k,i))}}}+{\overline{e}_{b}(k-1,i){\overline{e}_{f}(k,i)}}$
	${\displaystyle {\overline {e}}_{b}(k,i+1)={\frac {{\overline {e}}_{b}(k-1,i)-{\overline {\delta }}(k,i){\overline {e}}_{f}(k,i)}{\sqrt {(1-{\overline {\delta }}^{2}(k,i))(1-{\overline {e}}_{f}^{2}(k,i))}}}}$
	${\displaystyle {\overline {e}}_{f}(k,i+1)={\frac {{\overline {e}}_{f}(k,i)-{\overline {\delta }}(k,i){\overline {e}}_{b}(k-1,i)}{\sqrt {(1-{\overline {\delta }}^{2}(k,i))(1-{\overline {e}}_{b}^{2}(k-1,i))}}}}$
	피드포워드 필터
	${\displaystyle {\delta }}{D}(k,i)={\overline {\delta }}{D}}}{{delta }}}{delta }}{{b}^{ni){1-{{\overline{}}}{e,i){}}}}+{\overline{e}(k,i){\overline{e}_{b}(k,i)}}$
	${\displaystyle {\overline{e}(k,i+1)={\frac {1}{1}{\coverline{e}_{b}^{2}(k,i))(1-{{\overline {\delta }}}{D,i){2}(k,i)}}}[{\overline {{e}(k,i)-{\overline{\delta }}}{D}(k,i){\overline{e}_{b}(k,i)]}}}$
	끝
	끝

참고 항목

• 적응 필터
• 커널 적응 필터
• 최소 평균 제곱 필터
• 제로 강제 이퀄라이저

참조

• Hayes, Monson H. (1996). "9.4: Recursive Least Squares". Statistical Digital Signal Processing and Modeling. Wiley. p. 541. ISBN 0-471-59431-8.
• 사이먼 헤이킨, 프렌티스 홀, 2002, ISBN 0-13-048434-2
• M.H.A 데이비스, R.B.빈터, 확률적 모델링 및 제어, 스프링거, 1985년 ISBN 0-412-16200-8
• 웨이펑 류, 호세 프린시페, 사이먼 헤이킨, 커널 적응 필터링: 종합 소개, 존 와일리, 2010, ISBN 0-470-44753-2
• R.L. Plackett, 1950, Biometrica, 37, 149-157, ISSN 0006-3444의 최소 제곱의 일부 이론
• C.F.Gauss, Theoryia combinationis warnosiae, 1821, Werke, 4. Gottinge

메모들