나선 최적화 알고리즘

나선은 글로벌(파란색)과 집중(빨간색) 동작을 공유한다.

수학에서 Spiral Optimization(SPO) 알고리즘은 자연에서 Spiral 현상에 의해 영감을 받은 메타휴리스틱이다.

최초의 SPO 알고리즘은 2차원 나선형 모델을 기반으로 한 2차원 구속되지 않는^[1] 최적화를 위해 제안되었다.이것은 2차원 나선형 모델을 n차원 나선형으로 일반화함으로써 n차원 문제로 확대되었다.^[2]SPO 알고리즘에는 주기적인 강하 방향^[3] 설정과 수렴 설정 등 효과적인 설정이 있다.^[4]

은유

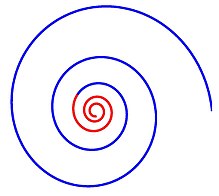
나선형 현상에 집중하게 된 동기는 로그 나선형을 생성하는 역학들이 다변화와 심화 행동을 공유한다는 통찰 때문이었다.다양화 동작은 글로벌 검색(탐색)에 효과가 있을 수 있으며, 강화 동작은 현재 발견된 양호한 솔루션(탐색)을 중심으로 집중적인 검색을 가능하게 한다.

알고리즘.

Spiral Optimization(SPO) 알고리즘

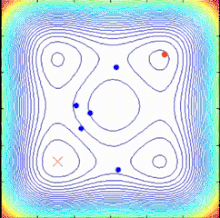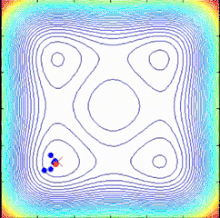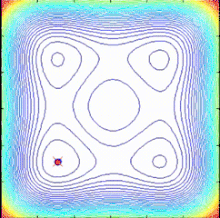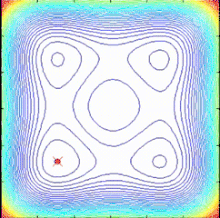
SPO 알고리즘은 객관적 함수 구배가 없는 다중점 검색 알고리즘으로 결정론적 동적 시스템으로 설명할 수 있는 다중 나선 모델을 사용한다.검색 지점이 현재 가장 좋은 지점으로 정의되는 공통 중심을 향한 로그 나선 궤적을 따르므로 더 나은 해결책을 찾을 수 있고 공통 센터를 업데이트할 수 있다.

최대 반복 $k_{\max }$ ${\$ 종료 기준)에 따른 최소화 문제에 대한 일반 SPO 알고리즘은 다음과 같다.

0) Set the number of search points  $m\geq 2$  and the maximum iteration number  $k_{\max }$ . 1) Place the initial search points  $x_{i}(0)\in \mathbb {R} ^{n}~(i=1,\ldots ,m)$  and determine the center  $x^{\star }(0)=x_{i_{\text{b}}}(0)$  $x^{\star }(0)=x_{i_{\text{b}}}(0)$ ,  ${\displaystyle \displaystyle i_{\text{b}}=\mathop {\text{argmin}} _{i=1,\ldots ,m}\{f(x_{i}(0))$  $\}}}$ 을 $\displaystyle i_{\text{b}}=\mathop {\text{argmin}} _{i=1,\ldots ,m}\{f(x_{i}(0))\}$ 를) $k=0$ 한  $k=0$  k $k=0$ = 0 {\ $displaystyle k$ 0 $}$  . 2) 규칙으로 $r(k)$  스텝 $r(k)$   $(k$  ){\ $displaystyle$ r(k)}을(를) 결정한다.3) Update the search points:  ${\displaystyle x_{i}(k+1)=x^{\star }(k)+r(k)R(\theta )(x_{i}(k)-x^{\star }(k))\quad (i=1,\ldots ,m).$ }4):)⋆(k+1)={x나는 b(k+1)(나는 b 만약 f(x(k+1))<>이름()⋆(k))),)⋆(k)( 그렇지 않으면),{\displaystyle x^{\star}(k+1)={\begin{경우}x_{i_{\text{b}}}(k+1)&,{\big(}{\text{만약}}f(x_{i_{\text{b}}}(k+1))<>f(x^{\star}(k)){\b은 센터를 업데이트합니다.ig)},\\x^만약 k= km그리고 4.9초 만 맥스{\displaystyle k=k_{\max{\star}(k)&,{\big(}{\text{ 그렇지 않으면}}{\big)},\end{경우}}}제가 거기 b)argmin 나는 1정도,…, m⁡{f(x나는(k+1))}{\displaystyle\displaystyle i_{\text{b}}=\mathop{\text{argmin}}_{i=1,\ldots ,m}\{f(x_{나는}(k+1)))}}. 5). k:=k+1{\displaystyle k:=k+1}설정합니다. }}만족한 다음  $x^{\star }(k)$   $x^{\star }(k)$ (  $){\displaystyle x^{\star }(k)}$ 을(를) 종료하고 출력한다 $x^{\star }(k)$  그렇지 않으면 2단계로 돌아가십시오.

설정

검색 성능은 복합 회전 행렬 $R(\theta )$ ( $R(\theta )$ ) ${\displaystyle$ R $(\theta$ $R(\theta )$ 단계 비율 $r(k)$ ( $r(k)$ k ) ${\displaystyle r(k$ 및 초기 지점 $x_{i}(0)~(i=1,\ldots ,m)$ i $x_{i}(0)~(i=1,\ldots ,m)$ ( $x_{i}(0)~(i=1,\ldots ,m)$ = $x_{i}(0)~(i=1,\ldots ,m)$ , $x_{i}(0)~(i=1,\ldots ,m)$ , $x_{i}(0)~(i=1,\ldots ,m)$ , $x_{i}(0)~(i=1,\ldots ,m)$ $displaystysty x_{i}(0)~(i=1,\ldots ,m)}$ 의 설정에 따라 달라진다 $x_{i}(0)~(i=1,\ldots ,m)$

설정 1(주기적 강하 방향 설정)

이 설정은 최대 반복 $k_{\max }$ ${\$ 아래의 높은 치수 문제에 효과적인 설정이다 $k_{\max }$ $R(\theta )$ ( $R(\theta )$ ) $R(\theta )$ 과 $R(\theta )$ x $x_{i}(0)~(i=1,\ldots ,m)$ ( $x_{i}(0)~(i=1,\ldots ,m)$ ${\displaystyle x_{i}(0)~(i=1,\ldots ,m)$ 의 조건을 함께 $x_{i}(0)~(i=1,\ldots ,m)$ 사용하면 나선형 모델이 주기적으로 하강 방향을 생성하도록 보장할 수 있다. $r(k)$ ( $r(k)$ ) ${\displaystyle$ r $(k)}$ 의 조건은 검색 종료 $k_{\max }$ $k_{\max }$ ${\$ 에 따른 주기적인 하강 방향을 활용하는 데 효과가 $r(k)$ 있다 $k_{\max }$

$R(\theta )$ ( $R(\theta )$ ) ${\displaystyle R(\$ $R(\theta )={\begin{bmatrix}0_{n-1}^{\top }&-1\\I_{n-1}&0_{n-1}\\\end{bmatrix}}$ $)}$ 을(를) $R(\theta )={\begin{bmatrix}0_{n-1}^{\top }&-1\\I_{n-1}&0_{n-1}\\\end{bmatrix}}$ 과 같이 $R(\theta )$ 설정하십시오. R ( $R(\theta )={\begin{bmatrix}0_{n-1}^{\top }&-1\\I_{n-1}&0_{n-1}\\\end{bmatrix}}$ ) $R(\theta )={\begin{bmatrix}0_{n-1}^{\top }&-1\\I_{n-1}&0_{n-1}\\\end{bmatrix}}$ = [ $R(\theta )={\begin{bmatrix}0_{n-1}^{\top }&-1\\I_{n-1}&0_{n-1}\\\end{bmatrix}}$ - $R(\theta )={\begin{bmatrix}0_{n-1}^{\top }&-1\\I_{n-1}&0_{n-1}\\\end{bmatrix}}$ I $R(\theta )={\begin{bmatrix}0_{n-1}^{\top }&-1\\I_{n-1}&0_{n-1}\\\end{bmatrix}}$ - $R(\theta )={\begin{bmatrix}0_{n-1}^{\top }&-1\\I_{n-1}&0_{n-1}\\\end{bmatrix}}$ $R(\theta )={\begin{bmatrix}0_{n-1}^{\top }&-1\\I_{n-1}&0_{n-1}\\\end{bmatrix}}$ - $R(\theta )={\begin{bmatrix}0_{n-1}^{\top }&-1\\I_{n-1}&0_{n-1}\\\end{bmatrix}}$ $R(\theta )={\begin{bmatrix}0_{n-1}^{\top }&-1\\I_{n-1}&0_{n-1}\\\end{bmatrix}}$ - 1 $R(\theta )={\begin{bmatrix}0_{n-1}^{\top }&-1\\I_{n-1}&0_{n-1}\\\end{bmatrix}}$ {\ $displaystyle$ R $(\theta )={\begin{bmatrix}0_{n-1}^{\$ n-1}-1\\top $}-$ 1\\\\\\\\1 $\$ pa\n\\n\\\n\\\\\n\\\\n\\\\\pa\n\\ $n-$ \ $I_{n-1}&0_{n-1}\\\end{bmatrix}}}$ where $I_{n-1}$ is the $(n-1)\times (n-1)$ identity matrix and $0_{n-1}$ is the $(n-1)\times 1$ zero vector.
$x_{i}(0)\in \mathbb {R} ^{n}$ 지점 $x_{i}(0)\in \mathbb {R} ^{n}$ ( 0 ) $^$ R n {\ $displaystyle x_{i}(0)\in \mathb$ { $(i=1,\ldots ,m)$ $}^{n$ $(i=1,\ldots ,m)$ = 1 $(i=1,\ldots ,m)$ , $(i=1,\ldots ,m)$ … , $(i=1,\ldots ,m)$ ) ${\displaystyle (i=$ 1,\ $ldots$ ,m $)}$ 을(으) 임의로 $(i=1,\ldots ,m)$ 배치하여 다음 조건을 충족하십시오.

${\displaystyle \min _{i=1,\ldots ,m}\{\max _{j=1,\ldots ,m}{\bigl \{}{\text{rank}}{\bigl [}d_{j,i}(0)~R(\theta )d_{j,i}(0)~~\cdots ~~R(\theta )^{2n-1}d_{j,i}(0){\b$ $d_{j,i}(0)=x_{j}(0)-x_{i}(0)$ $]}{\bigr \}}{\$ $d_{j,i}(0)=x_{j}(0)-x_{i}(0)$ $\}}}}{{{$ $d_{j,i}(0)=x_{j}(0)-x_{i}(0)$ ) = $d_{j,i}(0)=x_{j}(0)-x_{i}(0)$ ( $d_{j,i}(0)=x_{j}(0)-x_{i}(0)$ ) - $d_{j,i}(0)=x_{j}(0)-x_{i}(0)$ ( $d_{j,i}(0)=x_{j}(0)-x_{i}(0)$ ) $d_{j,i}(0)=x_{j}(0)-x_{i}(0)$ {\ $displaystyle d_{j,i$ }( $0)=x_-x_{i$ 이 조건은 거의 임의의 배치로 충족되므로 실제로는 아무런 점검도 되지 않는다는 점에 유의하십시오.

2단계에서 $r(k)$ $r(k)$ ( $r(k)=r={\sqrt[{k_{\max }}]{\delta }}~~~~{\text{(constant value)}}$ $){\displaystyle r(k)}$ 을(를) $r(k)=r={\sqrt[{k_{\max }}]{\delta }}~~~~{\text{(constant value)}}$ 과 같이 설정하십시오. r $r(k)=r={\sqrt[{k_{\max }}]{\delta }}~~~~{\text{(constant value)}}$ ( $r(k)=r={\sqrt[{k_{\max }}]{\delta }}~~~~{\text{(constant value)}}$ ) $r(k)=r={\sqrt[{k_{\max }}]{\delta }}~~~~{\text{(constant value)}}$ = r $r(k)=r={\sqrt[{k_{\max }}]{\delta }}~~~~{\text{(constant value)}}$ = $r(k)=r={\sqrt[{k_{\max }}]{\delta }}~~~~{\text{(constant value)}}$ $r(k)=r={\sqrt[{k_{\max }}]{\delta }}~~~~{\text{(constant value)}}$ $r(k)=r={\sqrt[{k_{\max }}]{\delta }}~~~~{\text{(constant value)}}$ ( $r(k)=r={\sqrt[{k_{\max }}]{\delta }}~~~~{\text{(constant value)}}$ ${\$ $\delta =1/k_{\max }$ = $\delta =1/k_{\max }$ / k $\delta =1/k_{\max }$ ${\displaystyle \max$ }, $\delta >0$ $\delta =10^{-3}$ = 1 $\delta =10^{-3}$ {\ $max$ }, Δ = $\delta =10^{-3}$ - 3 ${\$ ^{-3 $}$ 등 충분히 작은 $r(k)=r={\sqrt[{k_{\max }}]{\delta }}~~~~{\text{(constant value)}}$ $\delta >0$ = $\delta >0$ {\ $displaystystyle$ \p = 10 $^{-3$ ^[3]

설정 2(융합 설정)

This setting ensures that the SPO algorithm converges to a stationary point under the maximum iteration $k_{\max }=\infty$ . The settings of $R(\theta )$ and the initial points $x_{i}(0)~(i=1,\ldots ,m)$ are the same with the ab과대설정 1. $r(k)$ ( $r(k)$ ) $r(k)$ 의 설정은 다음과 $r(k)$ 같다.

2단계 0으로 r(k){\displaystyle r(k)}설정:;(k^{\star}\leqqk\leqq k^{\star}+2n-1),\\h&,(k\geqq k^{\star}+2n),\end{경우}}}이 k({\displaystyle k^{\star}}은 i. r(k)){1(k⋆ ≦ k≦ k⋆+2n− 1), h(k≧ k+2⋆ n),{\displaystyle r(k)={\begin{경우}1& 따르terationwhen the center is newly updated at Step 4) and $h={\sqrt[{2n}]{\delta }},\delta \in (0,1)$ such as $\delta =0.5$ . Thus we have to add the following rules about $k^{\star }$ to the Algorithm:

•(1단계)

k^{\star }=0

k^{\star }=0

=

k^{\star }=0

{\displaystyle

k

^{\star }=0}

.

• (4) x

x^{\star }(k+1)\neq x^{\star }(k)

(

x^{\star }(k+1)\neq x^{\star }(k)

+

x^{\star }(k+1)\neq x^{\star }(k)

)

x^{\star }(k+1)\neq x^{\star }(k)

x^{\star }(k+1)\neq x^{\star }(k)

(

x^{\star }(k+1)\neq x^{\star }(k)

) { (k )

x^{\star }(k+1)\neq x^{\star }(k)

\

displaystyle

x

^{}(k+1)\neq

x

^{\star }}}}

k^{\star }=k+1

=

k^{\star }=k+1

+ 1 {\

displaystyle

k

^{\star}=k+1

^[4]

미래 작품

위의 설정을 가진 알고리즘은 결정론적이다.따라서 일부 랜덤 연산을 통합하면 이 알고리즘이 글로벌 최적화를 위해 강력해진다.크루즈-두아르테 외 연구진은 나선형 탐색 궤도에 확률적 장애를 포함시킴으로써 그것을 증명했다.^[5]그러나 이 문은 더 이상의 연구에 열려 있다.
$k_{\max }$ 문제 등급(k max ${\$ 포함 $k_{\max }$ 에 따라 다변화와 심화 완화곡선 사이의 적절한 균형을 찾기 위해서는 성능을 향상시키는 것이 중요하다.

확장된 작품

SPO의 단순한 구조와 개념 때문에 많은 확장된 연구가 진행되어 왔다. 이러한 연구들은 SPO의 글로벌 검색 성과와 제안된 새로운 응용을 향상시키는데 도움을 주었다.^[6]^[7]^[8]^[9]^[10]^[11]

참조

^ Tamura, K.; Yasuda, K. (2011). "Primary Study of Spiral Dynamics Inspired Optimization". IEEJ Transactions on Electrical and Electronic Engineering. 6 (S1): 98–100. doi:10.1002/tee.20628.
^ Tamura, K.; Yasuda, K. (2011). "Spiral Dynamics Inspired Optimization". Journal of Advanced Computational Intelligence and Intelligent Informatics. 132 (5): 1116–1121. doi:10.20965/jaciii.2011.p1116.
^ ^a ^b Tamura, K.; Yasuda, K. (2016). "Spiral Optimization Algorithm Using Periodic Descent Directions". SICE Journal of Control, Measurement, and System Integration. 6 (3): 133–143. Bibcode:2016JCMSI...9..134T. doi:10.9746/jcmsi.9.134.
^ ^a ^b Tamura, K.; Yasuda, K. (2020). "The Spiral Optimization Algorithm: Convergence Conditions and Settings". IEEE Transactions on Systems, Man, and Cybernetics: Systems. 50 (1): 360–375. doi:10.1109/TSMC.2017.2695577. S2CID 126109444.
^ 크루즈-두아르테, J.M., 마틴-디아즈, I, 무노즈-민자레스, J.U. 산체스-갈린도, L.A., 아비나-세르반테스, J. G. 가르시아-페레스, A. & 코레아-셀리, C. R. (2017)확률적 나선형 최적화 알고리즘에 관한 1차 연구. 2017 IEEE 국제 전력, 전자 및 컴퓨팅(ROPC), 1–6. https://doi.org/10.1109/ROPEC.2017.8261609
^ Nasir, A. N. K.; Tokhi, M. O. (2015). "An improved spiral dynamic optimization algorithm with engineering application". IEEE Trans. Syst.,Man, Cybern., Syst. 45 (6): 943–954. doi:10.1109/tsmc.2014.2383995. S2CID 24253496.
^ Nasir, A. N. K.; Ismail, R.M.T.R.; Tokhi, M. O. (2016). "Adaptive spiral dynamics metaheuristic algorithm for global optimisation with application to modelling of a flexible system" (PDF). Appl. Math. Modell. 40 (9–10): 5442–5461. doi:10.1016/j.apm.2016.01.002.
^ Ouadi, A.; Bentarzi, H.; Recioui, A. (2013). "multiobjective design of digital filters using spiral optimization technique". SpringerPlus. 2 (461): 697–707. doi:10.1186/2193-1801-2-461. PMC 3786071. PMID 24083108.
^ Benasla, L.; Belmadani, A.; Rahli, M. (2014). "Spiral optimization algorithm for solving combined economic and Emission Dispatch". Int. J. Elect. Power & Energy Syst. 62: 163–174. doi:10.1016/j.ijepes.2014.04.037.
^ Sidarto, K. A.; Kania, A. (2015). "Finding all solutions of systems of nonlinear equations using spiral dynamics inspired optimization with clustering". Journal of Advanced Computational Intelligence and Intelligent Informatics. 19 (5): 697–707. doi:10.20965/jaciii.2015.p0697.
^ Kaveh, A.; Mahjoubi, S. (October 2019). "Hypotrochoid spiral optimization approach for sizing and layout optimization of truss structures with multiple frequency constraints". Engineering with Computers. 35 (4): 1443–1462. doi:10.1007/s00366-018-0675-6. S2CID 54457145.

[tamura11a-1] Tamura, K.; Yasuda, K. (2011). "Primary Study of Spiral Dynamics Inspired Optimization". IEEJ Transactions on Electrical and Electronic Engineering. 6 (S1): 98–100. doi:10.1002/tee.20628.

[tamura11b-2] Tamura, K.; Yasuda, K. (2011). "Spiral Dynamics Inspired Optimization". Journal of Advanced Computational Intelligence and Intelligent Informatics. 132 (5): 1116–1121. doi:10.20965/jaciii.2011.p1116.

[tamura16a-3] Tamura, K.; Yasuda, K. (2016). "Spiral Optimization Algorithm Using Periodic Descent Directions". SICE Journal of Control, Measurement, and System Integration. 6 (3): 133–143. Bibcode:2016JCMSI...9..134T. doi:10.9746/jcmsi.9.134.

[tamura17a-4] Tamura, K.; Yasuda, K. (2020). "The Spiral Optimization Algorithm: Convergence Conditions and Settings". IEEE Transactions on Systems, Man, and Cybernetics: Systems. 50 (1): 360–375. doi:10.1109/TSMC.2017.2695577. S2CID 126109444.

[5] 크루즈-두아르테, J.M., 마틴-디아즈, I, 무노즈-민자레스, J.U. 산체스-갈린도, L.A., 아비나-세르반테스, J. G. 가르시아-페레스, A. & 코레아-셀리, C. R. (2017)확률적 나선형 최적화 알고리즘에 관한 1차 연구. 2017 IEEE 국제 전력, 전자 및 컴퓨팅(ROPC), 1–6. https://doi.org/10.1109/ROPEC.2017.8261609

[nasir15a-6] Nasir, A. N. K.; Tokhi, M. O. (2015). "An improved spiral dynamic optimization algorithm with engineering application". IEEE Trans. Syst.,Man, Cybern., Syst. 45 (6): 943–954. doi:10.1109/tsmc.2014.2383995. S2CID 24253496.

[nasir16a-7] Nasir, A. N. K.; Ismail, R.M.T.R.; Tokhi, M. O. (2016). "Adaptive spiral dynamics metaheuristic algorithm for global optimisation with application to modelling of a flexible system" (PDF). Appl. Math. Modell. 40 (9–10): 5442–5461. doi:10.1016/j.apm.2016.01.002.

[ouadi13a-8] Ouadi, A.; Bentarzi, H.; Recioui, A. (2013). "multiobjective design of digital filters using spiral optimization technique". SpringerPlus. 2 (461): 697–707. doi:10.1186/2193-1801-2-461. PMC 3786071. PMID 24083108.

[benasla14a-9] Benasla, L.; Belmadani, A.; Rahli, M. (2014). "Spiral optimization algorithm for solving combined economic and Emission Dispatch". Int. J. Elect. Power & Energy Syst. 62: 163–174. doi:10.1016/j.ijepes.2014.04.037.

[sidarto15a-10] Sidarto, K. A.; Kania, A. (2015). "Finding all solutions of systems of nonlinear equations using spiral dynamics inspired optimization with clustering". Journal of Advanced Computational Intelligence and Intelligent Informatics. 19 (5): 697–707. doi:10.20965/jaciii.2015.p0697.

[KavehMahjoubi-11] Kaveh, A.; Mahjoubi, S. (October 2019). "Hypotrochoid spiral optimization approach for sizing and layout optimization of truss structures with multiple frequency constraints". Engineering with Computers. 35 (4): 1443–1462. doi:10.1007/s00366-018-0675-6. S2CID 54457145.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

Search