기준 대기 모델

기준 대기 모델은 대기의 이상적인 가스 특성(명칭: 압력, 온도, 밀도 및 분자량)이 어떻게 변화하는지, 주로 고도의 함수로서, 그리고 때로는 위도, 연중무휴 등의 함수로서도 설명한다. 정적 대기 모델은 시간을 제외하고 더 제한된 영역을 가진다. 세계기상기구는 "국제협약에 의해 대략 연중 중위도 조건을 대표하는 대기온도, 압력, 밀도의 가상적인 수직분포"로 정의한다.

대표적인 사용법은 압력 고도계 교정, 항공기 성능 계산, 항공기 및 로켓 설계, 탄도표, 기상도 등의 기초가 된다."^[1]

예를 들어, 미국 표준 대기는 해발 고도 함수로써 공기 온도, 압력 및 질량 밀도에 대한 값을 도출한다.

다른 정적 대기 모델에는 다른 출력이 있을 수도 있고, 고도 이외의 입력에 의존할 수도 있다.

기본 가정

대기를 구성하는 기체는 보통 이상적인 기체로 가정되는데, 이는 다음과 같다.

\rho ={\frac {MP}{RT}}

여기서 ρ은 질량 밀도, M은 평균 분자량, P는 압력, T는 온도, R은 이상적인 기체 상수다.

이 가스는 소위 "정전기"의 힘에 의해 제자리에 고정된다. 즉, 특정 고도에 있는 기체의 특정 층에 대해, 무게의 하향(행성을 향한) 힘, 그 위 층의 압력에 의해 작용하는 하향 힘, 그리고 아래 층의 압력에 의해 작용하는 상향 힘 등, 모두 합이 0이다. 수학적으로 이것은 다음과 같다.

PA-(P+{\text{d}P)A-(\rho A{d}h)g_{0}=0\,

{\d}P=-g_{0}\rho {\text}h\,

마지막으로, 시스템을 설명하는 이러한 변수는 시간에 따라 변하지 않는다. 즉, 정적 시스템이다.

g_0, 여기서 중력 가속도는 표준 중력(지구 표면이나 다른 큰 몸의 중력으로 인한 평균 가속도)과 같은 값을 갖는 상수로 사용된다. 단순성의 기초는 위도, 고도 또는 위치에 따라 달라지지 않는다. 이 모든 요인에 의한 변동은 약 1%에서 최대 50km이다. 보다 복잡한 모델, 이러한 변형을 설명하십시오.

몇 가지 예

모델에 따라 일부 가스 성질은 고도에 대해 일정하게 취급될 수 있다.

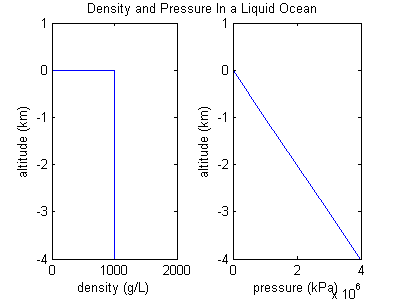
오션 예

만약 기체의 밀도가 지속된다면, 그것은 실제로 기체처럼 동작하지 않는 것이다. 대신에 그것은 압축할 수 없는 액체, 즉 액체처럼 행동하고 있고, 이 상황은 더 바다처럼 보인다. 밀도가 일정하다고 가정할 때, 머리 위의 대양의 무게는 그 깊이와 정비례하기 때문에, 압력 대 고도 그래프는 유지된 경사를 가질 것이다.

등온-변방성 근사치 및 척도 높이

이 대기 모델은 분자량과 온도 모두 광범위한 고도에 걸쳐 일정하다고 가정한다. 그러한 모델을 등온(정온)이라고 할 수 있다. 이상적인 가스 법칙에 대한 방정식에 일정한 분자량과 일정한 온도를 삽입하면 남은 두 변수인 밀도와 압력이 서로만 의존하는 결과를 낳는다. 이러한 이유로, 이 모델은 바롯이방성(밀도는 압력에 의해서만 달라진다)이라고도 불릴 수 있다.

등온-변환성 모델의 경우 밀도와 압력은 고도의 지수함수로 판명된다. P 또는 ρ이 초기값의 1/e로 떨어지기 위해 필요한 고도의 증가를 스케일 높이라고 한다.

H={\frac {RT}{Mg_{0}}}}

여기서 R은 이상적인 기체 상수, T는 온도, M은 평균 분자량, g는₀ 행성 표면의 중력 가속도다. 지구 대기의 특성으로 T=273 K와 M=29 g/mol 값을 사용했을 때 H = RT/Mg = (8.315*273)/ (29*9.8) = 7.99, 또는 약 8km로, 공교롭게도 에베레스트 산의 대략적인 높이에 해당한다.

등온 대기의 경우 ( $(1-{\frac {1}{e}})$ - $(1-{\frac {1}{e}})$ e $){\displaystyle (1-{\frac{1}{e})}$ 또는 대기 $(1-{\frac {1}{e}})$ 총 질량의 약 63%가 행성 표면과 하나의 척도 높이 사이에 존재한다. (특정 고도 이하의 총 공기 질량은 밀도 함수에 대해 통합하여 계산한다.)

대양의 예를 들면, 바다의 윗부분이나 "표면"의 밀도가 급격히 변화했다. 그러나 가스로 만들어진 대기의 경우 등가스의 급격한 전환이나 가장자리가 없다. 가스 대기는 우주가 될 정도로 얇아질 때까지 점점 더 밀도가 낮아진다.

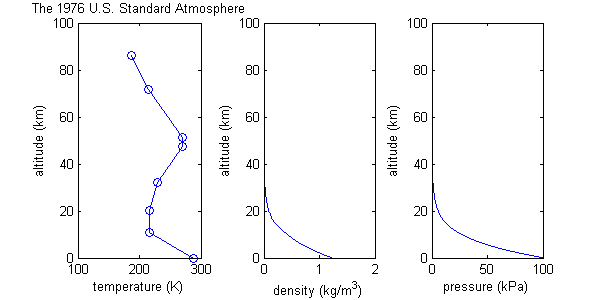
미국 스탠더드 분위기

미국 표준 대기 모형은 이상적인 기체 거동, 일정한 분자 중량을 포함한 등온-발광성 모델과 많은 동일한 가정으로 시작하지만, 보다 현실적인 온도 함수를 정의함으로써 달라지는데, 직선으로 연결된 8개의 데이터 지점, 즉 일정한 온도 구배 영역으로 구성되어 있다. (se)e 그래프) 물론 실제 대기는 이런 정확한 모양을 가진 온도분포를 가지고 있지는 않다. 온도 함수는 근사값이다. 압력 및 밀도에 대한 값은 이 온도 함수를 기반으로 계산되며, 일정한 온도 구배는 수학의 일부를 더 쉽게 만드는 데 도움이 된다.

NASA 지구 기준 대기 모델

NASA 지구 지구 기준 대기 모델(Earth-GRAM)은 표준 대기와는 달리 지리적 변동성, 광범위한 고도(궤도 고도에 대한 표면) 및 다른 월과 시간을 허용하는 설계 기준 대기권을 제공하기 위해 마셜 우주 비행 센터에 의해 개발되었다. 또한 난류 및 기타 대기 섭동 현상으로 인한 대기 매개변수의 공간 및 시간 섭동을 시뮬레이션할 수 있다. 그것은 포트란으로 쓰여진 컴퓨터 코드로 이용할^[2] 수 있다.^[3] GRM 시리즈는 금성, 화성, 해왕성, 토성 달 타이탄에 대한 대기 모델도 포함하고 있다.^[4]

지오포텐셜 고도

중력 가속도 g(z)는 위로 이동하면 행성의 중심에서 멀어지는 것을 의미하기 때문에 고도에 따라 감소한다.

g(z)={\frac {gm_{e}}{(r_{e}+z)^{2}}}

g 감소의 이 문제는 실제 기하학적 고도 z에서 "지오포텐셜 고도" h라고 불리는 추상화 h로 변환하는 것을 정의함으로써 다룰 수 있다.

h={\frac {r_{e}z}{r_{e}+z}}

h는 재산을 가지고 있다.

{\frac {}{}}g(z)dz=g_{0}dh

(

{\frac {}{}}g(z)dz=g_{0}dh

)

{\frac {}{}}g(z)dz=g_{0}dh

{\frac {}{}}g(z)dz=g_{0}dh

=

{\frac {}{}}g(z)dz=g_{0}dh

0

{\frac {}{}}g(z)dz=g_{0}dh

h

{\daystyle {\frac{}{}}{{}g

g_{0}=g(0)={\frac {Gm_{e}}{{r_{e}}^{2}}}

z)dz=g_{

g_{0}=g(0)={\frac {Gm_{e}}{{r_{e}}^{2}}}

}dh}

g_{0}=g(0)={\frac {Gm_{e}}{{r_{e}}^{2}}}

서

{\frac {}{}}g(z)dz=g_{0}dh

g

g_{0}=g(0)={\frac {Gm_{e}}{{r_{e}}^{2}}}

=

g_{0}=g(0)={\frac {Gm_{e}}{{r_{e}}^{2}}}

g_{0}=g(0)={\frac {Gm_{e}}{{r_{e}}^{2}}}

g_{0}=g(0)={\frac {Gm_{e}}{{r_{e}}^{2}}}

{\

}}:{

r_{

e}^

2}}:

00

}

기본적으로 중력이 고도에 따라 감소하는 대기를 통해 시험 질량을 z 높이까지 들어올리는 작업량이 gm이 해발에서 값인 g0과 동일하게 유지되는 대기를 통해 동일한 질량을 h 높이까지 들어올리는 작업량과 동일하다는 것이다.

이 지오포텐셜 고도 h는 정수 방정식에서 기하학적 고도 z 대신 사용된다.

공통 모델

미국 스탠더드 분위기는 가장 일반적인 모델 중 하나이다.
국제표준분위기(International Standard Freatment)는 관련 국제표준이다.
제트 표준 대기
NRLMSISE-00은 대기 과학에서 자주 사용되는 NRL의 최신 모델이다.
자키아 참조 대기(Jacchia Reference Freasure)는 여전히 우주선 역학에서 흔히 사용되는 구형 모델이다.

참고 항목

참조

^ National Oceanic and Atmospheric Administration; National Aeronautics and Space Administration; United States Air Force (October 1976), U. S. Standard Atmosphere, 1976 (PDF), Washington, D.C.: U. S. Government Printing Office, p. xiv
^ "Earth Global Reference Atmospheric Model (Earth-Gram) 2010", Software Catalog 2015–2016, NASA – Technology Transfer Program, retrieved 16 August 2016
^ Leslie, F.W.; Justus, C.G. (June 2011), The NASA Marshall Space Flight Center Earth Global Reference Atmospheric Model—2010 Version (PDF), NASA/TM—2011–216467, Marshall Space Flight Center, Alabama: National Aeronautics and Space Administration, retrieved 15 August 2016
^ Justh, Hilary L.; Justus, C. G.; Keller, Vernon W. (2006), "Global Reference Atmospheric Models, Including Thermospheres, for Mars, Venus and Earth", AIAA/AAS Astrodynamics Specialists Conference; 21–24 Aug. 2006; Keystone, CO; United States, doi:10.2514/6.2006-6394, hdl:2060/20060048492

외부 링크

[1] National Oceanic and Atmospheric Administration; National Aeronautics and Space Administration; United States Air Force (October 1976), U. S. Standard Atmosphere, 1976 (PDF), Washington, D.C.: U. S. Government Printing Office, p. xiv

[2] "Earth Global Reference Atmospheric Model (Earth-Gram) 2010", Software Catalog 2015–2016, NASA – Technology Transfer Program, retrieved 16 August 2016

[3] Leslie, F.W.; Justus, C.G. (June 2011), The NASA Marshall Space Flight Center Earth Global Reference Atmospheric Model—2010 Version (PDF), NASA/TM—2011–216467, Marshall Space Flight Center, Alabama: National Aeronautics and Space Administration, retrieved 15 August 2016

[4] Justh, Hilary L.; Justus, C. G.; Keller, Vernon W. (2006), "Global Reference Atmospheric Models, Including Thermospheres, for Mars, Venus and Earth", AIAA/AAS Astrodynamics Specialists Conference; 21–24 Aug. 2006; Keystone, CO; United States, doi:10.2514/6.2006-6394, hdl:2060/20060048492

[1]

[2]

[3]

[4]

Search