스텝 감지

통계 및 신호 처리에서 스텝 감지(스텝 스무딩, 스텝 필터링, 변속 감지, 점프 감지 또는 에지 감지라고도 함)는 시계열 또는 신호의 평균 수준에서 갑작스러운 변화(스텝, 점프, 변속)를 찾는 과정이다.보통 변경검출 또는 변경점검출로 알려진 통계적 방법의 특수한 경우로 간주된다.종종 단계가 작고 시계열은 어떤 종류의 소음으로 인해 변질되는데, 이것은 그 단계가 소음으로 가려질 수 있기 때문에 문제를 어렵게 만든다.따라서 통계 및/또는 신호 처리 알고리즘이 필요한 경우가 많다.null

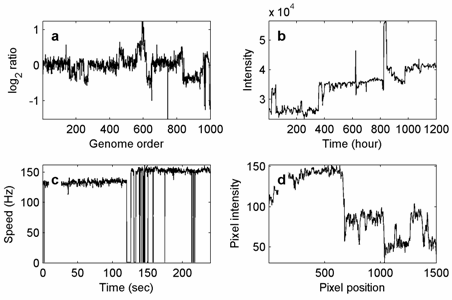
이번 조치로 탐지 문제가 다국어 및 여러 과학 기술적 맥락에서, 통계적 프로세스 control[1](그 관리도 가장 직접적으로 관련 법)에서 예를 들어, 탐험 지구 물리학(어디서 문제가 층서 zones[2]에well-log 녹화에서 제외 시켜야는 것이다), 유전학에서의 마이크로 어레이를 분리시키는(그 문제 d에서 발생한다ata에유사한 복사 번호 체계^[3]) 및 생물물리학(시간 위치 추적에^[4] 기록된 분자 기계의 상태 전환).2D 신호의 경우 이미지 처리를 위해 에지 검출 관련 문제가 집중적으로 연구됐다.^[5]null

알고리즘

데이터가 도착하는 대로, 그리고 도착하는 대로 스텝 탐지를 실시해야 할 때, 보통 온라인 알고리즘이 사용되며,^[6] 이는 순차 분석의 특별한 사례가 된다.그러한 알고리즘은 평균의 변화에 적용되는 고전적인 누적합[CUSUM] 방법을 포함한다.^[7]

이와는 대조적으로, 오프라인 알고리즘은 데이터가 수신된 지 오래 후에 잠재적으로 데이터에 적용된다.디지털 데이터에서 스텝 감지를 위한 대부분의 오프라인 알고리즘은 하향식, 상향식, 슬라이딩 윈도우 또는 글로벌 방식으로 분류할 수 있다.null

하향식

이러한 알고리즘은 단계가 없다는 가정에서부터 시작하여 가능한 후보 단계를 한 번에 하나씩 도입하고, 각 후보가 일부 기준(예: 추정된 조각 상수 신호의 최소 제곱 적합도 등)을 최소화하는 기준을 찾기 위해 시험한다.예를 들어, 지구물리학적 문제에서 처음 연구된 단계적 점프 배치 알고리즘이 현대의 생물물리학에서 최근 사용법을 찾아냈다.^[2][8]null

상향식

상향식 알고리즘은 하향식 방법에 대한 "반대" 접근방식을 취하며, 먼저 디지털 신호의 모든 샘플 사이에 단계가 있다고 가정하고, 이후 모든 후보 병합에 대해 테스트한 일부 기준에 따라 연속적으로 단계를 병합한다.null

미닫이창

신호의 작은 "창"을 고려함으로써, 이 알고리즘은 윈도우 내에서 스텝이 발생했다는 증거를 찾는다.윈도우가 시계열을 가로질러 한 번에 한 단계씩 "슬라이드"된다.스텝에 대한 증거는 예를 들어 2-표본 학생의 t-검정을 사용하여 통계적 절차에 의해 시험된다.또는 중위수 필터와 같은 비선형 필터를 신호에 적용한다.이러한 필터는 갑작스러운 단계를 유지하면서 소음을 제거하려고 시도한다.null

글로벌

글로벌 알고리즘은 전체 신호를 한 번에 고려하고, 어떤 종류의 최적화 절차에 의해 신호의 단계를 찾으려고 시도한다.알고리즘에는 파장 방법 ^[9]및 볼록 최적화 방법을 사용하는 총 변화 디노잉이 포함된다.단계를 마르코프 체인으로 모델링할 수 있는 곳에서는 히든 마르코프 모델도 자주 사용된다(생물물리학계에서^[10] 인기 있는 접근법).평균의 고유 값이 몇 개만 있는 경우 k-평균 군집화도 사용할 수 있다.null

스텝 감지를 위한 선형 대 비선형 신호 처리 방법

단계와 (독립적) 노이즈에는 이론적으로 무한한 대역폭이 있고 푸리에 기초가 중복되기 때문에, 단계 탐지에 대한 신호 처리 접근법은 일반적으로 로우패스 필터와 같은 고전적인 스무딩 기법을 사용하지 않는다.대신 대부분의 알고리즘은 명시적으로 비선형적이거나 시간 변동을 일으킨다.^[11]null

스텝 감지 및 조각상수 신호

스텝 검출의 목적은 신호의 평균에서 일련의 순간 점프를 찾는 것이기 때문에, 원하는, 기저에 있는 평균 신호는 조각처럼 일정하다.이러한 이유로, 단계 검출은 노이즈에 의해 손상된 조각상수 신호를 복구하는 문제로 이익적으로 볼 수 있다.조각과 같은 상수 신호에는 두 가지 보완 모델이 있다. 즉, 노트가 몇 개 있는 0도 스플라인 또는 몇 개의 고유한 수준을 가진 레벨 세트로 한다.따라서 스텝 감지를 위한 많은 알고리즘은 0도 스플라인 피팅 또는 레벨 세트 복구 방법 중 하나로 가장 잘 이해된다.null

레벨 세트 복구로 단계 감지

평균의 고유 값이 몇 개만 있는 경우 k-평균 군집화 또는 평균 이동과 같은 군집화 기법이 적합하다.이러한 기법은 기초적인 조각의 상수 신호에 대한 레벨 세트 설명을 찾는 방법으로 가장 잘 이해된다.null

0도 스플라인 피팅으로 스텝 감지

많은 알고리즘이 층계를 감지하기 위해 노이즈 신호에 0도 스플라인을 명시적으로 적합시키지만(단계별 점프 배치 방법^[2][8] 포함), 일부 변환 후 스플라인 피팅 방법으로도 볼 수 있는 다른 인기 알고리즘(예:^[12] 총 변동 디노잉)도 있다.null

조각별 상수 디노이즈에 의한 일반화된 스텝 감지

위에서 언급한 모든 알고리즘은 특정한 상황에서 특정한 장단점을 가지고 있지만, 이러한 스텝 감지 알고리즘의 수가 놀라울 정도로 많은 것은 보다 일반적인 알고리즘의 특수한 경우다.^[11]이 알고리즘은 글로벌 기능의 최소화를 포함한다.^[13]

${\displaystyle H[m]=\sum _{i=1}^{N}\sum _{j=1}{j=1}^{n}\Lambda (x_{i}-m_{j}-m_{j},x_{i}-x_{j},i-j)}$

(1)

여기서 x for_i i = 1, ...., N은 길이 N의 이산 시간 입력 신호, m은_i 알고리즘의 신호 출력이다.출력 신호 m에 대해 H[m]를 최소화하는 것이 목표다.$\lambda {\displaystyle \mathrm{}}$ ${\$ 함수의 형태가 특정 알고리즘을 결정한다$$.예를 들어, 다음을 선택하십시오.

${\displaystyle \Lambda ={\frac {1}{2}}\왼쪽 x_{i}-m_{j}\오른쪽 ^{2}I(i-j=0)+\gamma \왼쪽 m_{i}-m_{j}\오른쪽 I(i-j=1)}$

여기서 조건 S가 거짓인 경우 I(S) = 0이고, 그 이외의 조건 S가 정규화 $매개{\displaystyle }$ 변수 ${\displaystyle \gamma }$을(를) 사용하여 총 변동 데노화 알고리즘을 얻는다$.$ 마찬가지로:

${\displaystyle \Lambda =\min \left\{\frac {1}{1}2}}\왼쪽 m_{i}-m_{j}\right ^{2},W\right\}}}}}$

입력 신호 x로 초기화된 적응형 스텝 크기 오일러 통합기를 사용할 때 평균 시프트 알고리즘으로 유도한다.^[13]여기서 W > 0은 평균 시프트 커널의 지원을 결정하는 파라미터다.또 다른 예는 다음과 같다.

${\displaystyle \Lambda ={\frac {1-\exp(-\beta m_{i}-m_{j} ^{2}/2)}{\beta }}{\cdot I(i-j \leq W)}}$

양자 필터로 이어지며, 여기서 > ${\$은 톤 커널 파라미터, W는 공간 커널 지원이다.그러나 또 다른 특별한 경우는 다음과 같다.

${\displaystyle \Lambda ={\frac {1}{2}}\왼쪽 x_{i}-m_{j}\오른쪽 ^{2}I(i-j=0)+\\gamma \왼쪽 m_{i}-m_{j}\오른쪽 ^{0}I(i-j=1)}$

신호에 0도 스플라인을 탐욕스럽게 맞추려는 알고리즘 그룹을 지정한다.^[2][8]여기서 ${\displaystyle x^{}}$ ${\displaystyle 0^{\mathrm{}}}$ ${\$ x$\우측 ^{$0}}은(는) 0으로 정의되고 다른 하나는 0으로 정의된다$$.null

$\lambda {\displaystyle \mathrm{}}$ ${\$의 특정 선택에 의해 정의된 등식 (1)의 많은 함수들은$$ 볼록하다. 볼록 최적화 방법을 사용하여 최소화할 수 있다.여전히 다른 것들은 비컨벡스지만 이러한 기능들을 최소화하기 위한 다양한 알고리즘이 고안되었다.^[13]null

Potts 모델을 사용한 스텝 감지

스텝 감지를 위한 고전적인 변동 방법은 Potts 모델이다.비컨벡스 최적화 문제에 의해 주어진다.

${\displaystyle u^{*}=\arg \min _{u\in \mathb {R}^{{N}}\nabla u\ \{0}+\ u-x\{p}^{p}}}}}}$

The term ${\displaystyle \ \nabla u\ _{0}=\#\{i:u_{i}\neq u_{i+1}\}}$ penalizes the number of jumps and the term ${\displaystyle \ u-x\ _{p}^{p}=\sum _{i=1}^{N} u_{i}-x_{i} ^{p}}$ measures fidelity to data x.변수 > > 0은 규칙성과 데이터 충실도 사이의 절충을 제어한다.미니마이저 $∗{\$은(는) 조각처럼 일정하므로 경사가 0이 아닌 위치 steps ${\displaystyle {}^{}}\ast {\displaystyle \mathrm{}}$${\displaystyle }$${\$${\displaystyle }$$p{\displaystyle }$ = ${\displaystyle 2}$$${\$displaystyle p=1}$의 경우 Pots 문제의 정확한 해결책을 제공하는 빠른 알고리즘이 있다$$.${\displaystyle O}$( ${\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$)${\displaystyle O(N^{2})}$.

참고 항목

• 시계열 분할

참조

외부 링크

• PWCTools: 조각처럼 일정한 디노이즈로 스텝을 감지할 수 있는 유연한 Matlab 및 Python
• Pottslab: Potts 모델에 기초한 조각 상수 추정을 위한 Mattlab 도구 상자