응력 강도 계수 K {\displaystyle K} 균열 끝이나 노치 부근의 응력 상태("스트레스 강도")를 예측하기 위해 골절 역학 에서 사용된다.[1] 균질하고 선형적 인 탄성물질에 주로 적용되는 이론적 구조로 부서지기 쉬운 재료의 고장 기준을 제공하는 데 유용하며, 손상내성 규율에서 중요한 기법이다. 크랙 팁에서 소량 양보
K {\displaystyle K} 노치 의 크기 및 위치, 재료에 대한 하중의 크기와 분포에 따라 다음과 같이 쓸 수 있다.[2] [3]
K = σ π a f ( a / W ) {\displaystyle K=\sigma {\sqrt {\pi a}\,f(a/W)}
여기 f W {\displaystyle f(a/W)} {\displaystyle a} 시료 {\displaystyle W} σ {\displaystyle \sigma (
선형 탄성 이론은 균열 팁 부근의 극좌표 ( r { displaystyle \sigma _{ij})
σ i j ( r , θ ) = K 2 π r f i j ( θ ) + h i g h e r o r d e r t e r m s {\displaystyle \sigma _{ij}(r,\theta )={\frac {K}{\sqrt{2\pi r}}\,f_{ij}(\theta )+\,\,\,\\rm {higher\,orderms}}}} 여기서 K {\displaystyle K} × {\displaystyle \times } 1/2 단위 포함f displaystyle f_ }} 이론적으로 r {\displaystyle r} σ i j {\ displaystyle \sigma _{ij} ∞ {\displaystyle \infty } [5] 그러나 일반적으로 가소성 은 재료의 항복 강도를 초과하는 응력에서 발생하며 선형 탄성 용액은 더 이상 적용되지 않기 때문에 실질적으로 이 관계는 끝(작은 r {\displaystyle }) 그럼에도 크랙팁 플라스틱 존이 균열 길이에 비해 작을 경우 균열 팁 부근의 점근 응력 분포가 여전히 적용 가능하다.
다양한 모드의 응력 강도 계수 Mode I, Mode II 및 Mode III 균열 하중 1957년 G. 어윈 은 균열 주위의 응력이 응력 강도 인자 라는 스케일링 인자의 관점에서 표현될 수 있다는 것을 발견했다. 그는 임의 하중에 따른 균열이 세 가지 유형의 선형 독립 균열 모드로 해결될 수 있다는 것을 발견했다.[6] 이러한 하중 유형은 그림에서와 같이 모드 I, II 또는 III로 분류된다. 모드 I은 균열 표면이 직접 분리되는 개방(텐실 ) 모드다. 모드 II는 균열 표면이 균열의 선행 가장자리에 수직인 방향으로 서로 미끄러지는 슬라이딩(평면 내 전단 ) 모드다. 모드 III는 균열 표면이 서로 상대적이며 균열의 앞쪽 가장자리에 평행하게 이동하는 찢김(반면 전단) 모드다. 모드 I은 엔지니어링 설계에서 가장 일반적인 부하 유형이다.
세 가지 모드에 대한 응력 강도 계수를 지정하기 위해 다른 첨자를 사용한다. 모드 I의 응력 강도 계수는 KI {\ displaystyle K_{\rm{I}} 모드 II 응력 강도 계수, K I {\ displaystyle K_{\rm II III {\ displaystyle K_{\rm }} ( 이러한 요인은 공식적으로 다음과 같이 정의된다.[7]
K I = 임이 있는 r → 0 2 π r σ y y ( r , 0 ) K I I = 임이 있는 r → 0 2 π r σ y x ( r , 0 ) K I I I = 임이 있는 r → 0 2 π r σ y z ( r , 0 ) . {\displaystyle {\begin}K_{\rm {I}&=\lim_{r\rightarrow 0}{\sqrt{2\pi r}\\sigma _{y}(r,0)\K_{\rm {\rm} II}&=\lim _{r\오른쪽 화살표 0}{{r\sqrt{2\pi r}\\sigma _{yx}(r,0)\\\\rm {III}&=\lim_{r\오른쪽 화살표 0}{r\sqr\sqrt{2\pi r}\,\}\sigma _{{yz},r,r,0},},0\c,}\c,}\c. \end{정렬}}} 응력 및 변위장 방정식 KI {\ displaystyle K_{\rm{I}} [6]
{ σ x x σ y y σ x y } = K I 2 π r cos θ 2 { 1 − sin θ 2 sin 3 θ 2 1 + sin θ 2 sin 3 θ 2 sin θ 2 cos 3 θ 2 } {\displaystyle \left\{{\begin{aligned}\sigma _{xx}\\\sigma _{yy}\\\sigma _{xy}\end{aligned}}\right\}={\frac {K_{\rm {I}}}{\sqrt {2\pi r}}}\cos {\frac {\theta }{2}}\left\{{\begin{aligned}1-\sin {\frac {\theta }{2}}\sin {\frac {3\theta }{2}}\\1+\sin {\frac {\theta }{2}}\sin {\frac {3\theta }{2}}\\\sin {\frac {\theta }{2}}\cos {\frac {3\theta }{2}}\end{aligned}}\right\}} 그리고
{ σ r r σ θ θ σ r θ } = K I 2 π r cos θ 2 { 1 + sin 2 θ 2 cos 2 θ 2 sin θ 2 cos θ 2 } {\displaystyle \left\{{\begin{aligned}\sigma _{rr}\\\sigma _{\theta \theta }\\\sigma _{r\theta }\end{aligned}}\right\}={\frac {K_{\rm {I}}}{\sqrt {2\pi r}}}\cos {\frac {\theta }{2}}\left\{{\begin{aligned}1+\sin ^{2}{\frac {\theta }{2}}\\\cos ^{2}{\frac {\theta }{2}}\\\sin {\frac {\theta }{2}}\cos {\frac {\theta }{2}}\end{aligned}}\right\}} σ z z = ν 1 ( σ x x + σ y y ) = ν 1 ( σ r r + σ θ θ ) {\displaystyle \sigma _{zz}=\nu _{1}(\sigma _{xx}+\sigma _{yy})=\nu _{1}(\sigma _{rr}+\sigma _{\theta \theta })} σ z σ z σ z σ z 0 {\displaystyle \sigma _ma _{ sigma _{rz sigma _{\teta }=0} 변비는
{ u x u y } = K I 2 E r 2 π { ( 1 + ν ) [ ( 2 κ − 1 ) cas θ 2 − cas 3 θ 2 ] ( 1 + ν ) [ ( 2 κ + 1 ) 죄를 짓다 θ 2 − 죄를 짓다 3 θ 2 ] } {\displaystyle \left\{\begin}u_{x}\u_{y}\end}{y}}}={\fract}{K_{\rm{I}}}{2}}{2} E}}{\sqrt {\frac {r}{2\pi }}}\left\{{\begin{aligned}(1+\nu )\left[(2\kappa -1)\cos {\frac {\theta }{2}}-\cos {\frac {3\theta }{2}}\right]\\(1+\nu )\left[(2\kappa +1)\sin {\frac {\theta }{2}}-\sin {\frac {3\theta }{2}}\right]\end{aligned}}\right\}} { u r u θ } = K I 2 E r 2 π { ( 1 + ν ) [ ( 2 κ − 1 ) cas θ 2 − cas 3 θ 2 ] ( 1 + ν ) [ − ( 2 κ + 1 ) 죄를 짓다 θ 2 + 죄를 짓다 3 θ 2 ] } {\displaystyle \left\{\begin{ligned}u_{r}\u_{\theta }\ended}}\right\}={\fract}{K_{\rm {I}}}{2} E}}{\sqrt {\frac {r}{2\pi }}}\left\{{\begin{aligned}(1+\nu )\left[(2\kappa -1)\cos {\frac {\theta }{2}}-\cos {\frac {3\theta }{2}}\right]\\(1+\nu )\left[-(2\kappa +1)\sin {\frac {\theta }{2}}+\sin {\frac {3\theta }{2}}\right]\end{aligned}}\right\}} u z = − ( ν 2 z E ) ( σ x x + σ y y ) = − ( ν 2 z E ) ( σ r r + σ θ θ ) {\displaystyle u_{z}=-\left({\frac {\nu _{2}z}{E}}\right)(\sigma _{xx}+\sigma _{yy})=-\left({\frac {\nu _{2}z}{E}}\right)(\sigma _{rr}+\sigma _{\theta \theta })} 여기서, 평면 응력 조건의 경우
κ 3 ν ν {\ displaystyle \capa ={\frac {(3-\nu )}}}}, ν 1 0 {\displaystyle \nu _ {1}=0 ν 2 {\displaystyleane nu nu nu 그리고 평면 변형용.
κ 4 ν {\displaystyle \kappa (3-4\nu )}, ν ν {\displaystyle \nu _{1}=\nu }, ν 0 {\displaystyle \nu nu 2}=0 모드 II의 경우
{ σ x x σ y y σ x y } = K I I 2 π r { − 죄를 짓다 θ 2 ( 2 + cas θ 2 cas 3 θ 2 ) 죄를 짓다 θ 2 cas θ 2 죄를 짓다 3 θ 2 cas θ 2 ( 1 − 죄를 짓다 θ 2 죄를 짓다 3 θ 2 ) } {\displaystyle \left\{\begin{arged}\sigma _{xx}\\\\sigma _{y}\nd{xy}\light\}={\fract}{K_{\rm} II}}}{\sqrt {2\pi r}}}\left\{{\begin{aligned}-\sin {\frac {\theta }{2}}(2+\cos {\frac {\theta }{2}}\cos {\frac {3\theta }{2}})\\\sin {\frac {\theta }{2}}\cos {\frac {\theta }{2}}\sin {\frac {3\theta }{2}}\\\cos {\frac {\theta }{2}}(1-\sin {\frac {\theta }{2}}\sin {\frac {3\theta }{2}})\end{aligned}}\right\}} 그리고
{ σ r r σ θ θ σ r θ } = K I I 2 π r { sin θ 2 ( 1 − 3 sin 2 θ 2 ) − 3 sin θ 2 cos 2 θ 2 cos θ 2 ( 1 − 3 sin 2 θ 2 ) } {\displaystyle \left\{{\begin{aligned}\sigma _{rr}\\\sigma _{\theta \theta }\\\sigma _{r\theta }\end{aligned}}\right\} ={\frac {K_{\rm { II}}}{\sqrt {2\pi r}}}\left\{{\begin{aligned}\sin {\frac {\theta }{2}}(1-3\sin ^{2}{\frac {\theta }{2}})\\-3\sin {\frac {\theta }{2}}\cos ^{2}{\frac {\theta }{2}}\\\cos {\frac {\theta }{2}}(1-3\sin ^{2}{\frac {\theta }{2}})\end{aligned}}\right\}} σ z z = ν 1 ( σ x x + σ y y ) = ν 1 ( σ r r + σ θ θ ) {\displaystyle \sigma _{zz}=\nu _{1}(\sigma _{xx}+\sigma _{yy})=\nu _{1}(\sigma _{rr}+\sigma _{\theta \theta })} σ z σ z σ z σ z 0 {\displaystyle \sigma _ma _{ sigma _{rz sigma _{\teta }=0} { u x u y } = K I I 2 E r 2 π { ( 1 + ν ) [ ( 2 κ + 3 ) 죄를 짓다 θ 2 + 죄를 짓다 3 θ 2 ] − ( 1 + ν ) [ ( 2 κ − 3 ) cas θ 2 + cas 3 θ 2 ] } {\displaystyle \left\{\begin}u_{x}\\u_{y}\end}\ligned}\right\}={\fract {K_{\rm} II}}}{2E}}{\sqrt {\frac {r}{2\pi }}}\left\{{\begin{aligned}(1+\nu )\left[(2\kappa +3)\sin {\frac {\theta }{2}}+\sin {\frac {3\theta }{2}}\right]\\-(1+\nu )\left[(2\kappa -3)\cos {\frac {\theta }{2}}+\cos {\frac {3\theta }{2}}\right]\end{aligned}}\right\}} { u r u θ } = K I I 2 E r 2 π { ( 1 + ν ) [ − ( 2 κ − 1 ) 죄를 짓다 θ 2 + 3 죄를 짓다 3 θ 2 ] ( 1 + ν ) [ − ( 2 κ + 1 ) cas θ 2 + 3 cas 3 θ 2 ] } {\displaystyle \left\{\begin}u_{r}\u_{\theta }\ended{regated}}\right\}={\fract {K_{\rm {} II}}}{2E}}{\sqrt {\frac {r}{2\pi }}}\left\{{\begin{aligned}(1+\nu )\left[-(2\kappa -1)\sin {\frac {\theta }{2}}+3\sin {\frac {3\theta }{2}}\right]\\(1+\nu )\left[-(2\kappa +1)\cos {\frac {\theta }{2}}+3\cos {\frac {3\theta }{2}}\right]\end{aligned}}\right\}} u z = − ( ν 2 z E ) ( σ x x + σ y y ) = − ( ν 2 z E ) ( σ r r + σ θ θ ) {\displaystyle u_{z}=-\left({\frac {\nu _{2}z}{E}}\right)(\sigma _{xx}+\sigma _{yy})=-\left({\frac {\nu _{2}z}{E}}\right)(\sigma _{rr}+\sigma _{\theta \theta })} 마지막으로, 모드 III의 경우
{ σ x z σ y z } = K I I I 2 π r { − 죄를 짓다 θ 2 cas θ 2 } {\displaystyle \left\{{\begin{aligned}\sigma _{xz}\\\sigma _{yz}\end{aligned}}\right\}={\frac {K_{\rm {III}}}{\sqrt {2\pi r}}}\left\{{\begin{aligned}-\sin {\frac {\theta }{2}}\\\cos {\frac {\theta }{2}}\end{aligned}}\right\}} { σ r z σ θ z } = K I I I 2 π r { 죄를 짓다 θ 2 cas θ 2 } {\displaystyle \left\{{\begin{aligned}\sigma _{rz}\\\sigma _{\theta z}\end{aligned}}\right\}={\frac {K_{\rm {III}}}{\sqrt {2\pi r}}}\left\{{\begin{aligned}\sin {\frac {\theta }{2}}\\\cos {\frac {\theta }{2}}\end{aligned}}\right\}} with σ x x = σ y y = σ r r = σ θ θ = σ z z = σ x y = σ r θ = 0 {\displaystyle \sigma _{xx}=\sigma _{yy}=\sigma _{rr}=\sigma _{\theta \theta }=\sigma _{zz}=\sigma _{xy}=\sigma _{r\theta }=0}
u z = 2 K I I I E r 2 π { 2 ( 1 + ν ) sin θ 2 } {\displaystyle u_{z}={\frac {2K_{\rm {III}}}{E}}{\sqrt {\frac {r}{2\pi }}}\left\{2(1+\nu )\sin {\frac {\theta }{2}}\right\}} u u u u θ 0 {\displaystyle u_{x}=u_{y}={r}=u_ teta }=0}
에너지 방출률 및 J-적분율과의 관계 평면 응력 조건에서 순수 모드 I 또는 순수 모드 II 하중의 균열에 대한 변형 에너지 방출 속도 (G {\ 스타일 G}
G I = K I 2 ( 1 E ) {\displaystyle G_{\rm {I}=K_{\rm {I}^{2}\왼쪽({\frac {1}{E}\오른쪽)} G I I = K I I 2 ( 1 E ) {\displaystyle G_{\rm { II}}}=K_{\rm { II}^{2}\왼쪽({\frac {1}{E}\오른쪽)} 여기 E {\displaystyle E} 영의 계량형 이고 mod {\displaystyle \nu} 포아송 비율이다. 재료는 등방성, 균질, 선형 탄성인 것으로 가정한다. 균열은 초기 균열 방향을 따라 확장되는 것으로 가정되었다.
평면 변형 조건의 경우 등가 관계가 약간 더 복잡하다.
G I = K I 2 ( 1 − ν 2 E ) {\displaystyle G_{\rm{I}=K_{\rm{I}^{2}\왼쪽({\frac {1-\nu ^{2}}-{E}\오른쪽)\,},} G I I = K I I 2 ( 1 − ν 2 E ) . {\displaystyle G_{\rm { II}}}=K_{\rm { II}^{2}\왼쪽({\frac {1-\nu ^{2}}:{E}\오른쪽)\, } 순수 모드 III 로딩의 경우,
G I I I = K I I I 2 ( 1 2 μ ) = K I I I 2 ( 1 + ν E ) {\displaystyle G_{\rm {III}=K_{\rm {II}^{2}\왼쪽({\frac {1}{2\mu }}}\오른쪽) =K_{\rm{II}^{2}\왼쪽({\frac {1+\nu }{E}\오른쪽)} 여기서 μ[\displaystyle \mu } 전단 계수 다. 평면 변형률의 일반 하중의 경우 선형 조합은 다음을 지탱한다.
G = G I + G I I + G I I I . {\displaystyle G=G_{\rm {I}+G_{\rm {II}+G_{\rm {II}\,.} 세 가지 모드에 대한 기여도를 추가하여 평면 스트레스에 대해서도 유사한 관계를 얻는다.
위의 관계는 또한 J-적분성 을 스트레스 강도 인자에 연결하는 데 사용될 수 있다.
G = J = ∫ Γ ( W d x 2 − t ⋅ ∂ u ∂ x 1 d s ) . {\displaystyle G=J=\int _{\Gamma }왼쪽(W~dx_{2}-\mathbf {t} \cdot {\cfrac {\partial \mathbf {u}{}{\partial x_{1}~ds\rig)\, } 임계 응력 강도 계수 응력 강도 계수 K {\displaystyle K Y {\displaystyle Y}( 어떤 모드 상황에서든 응력 강도는 재료에 가해지는 하중에 정비례한다. 재료로 매우 날카로운 균열, 즉 V노트 를 만들 수 있다면 KI {\ 디스플레이스타일 K_{\mathrm{I}}}}} 평면 변형률 에서 모드 I 로딩에 대해 결정된 이 임계값을 재료의 임계 파괴 강도(KI {\ displaystyle K_{\mathrm{Iic K I c {\ displaystyle K_{\mathrm {Iic}}}}}}} 3/2 )에 곱한 응력 단위가 있다 KI c {\ displaystyle K_{\mathrm {Ic}} KI c {\ displaystyle K_{\mathrm {Ic}}}}} Mode I 임계 응력 강도 계수 KI c {\ displaystyle K_{\mathrm {Iic
광택은 균열을 감지할 수 없다. 일반적으로 균열이 보이면 응력 강도 인자에[citation needed 의해 예측된 임계 응력 상태 에 매우 가깝다.
G-크리온 G-기준 은 임계 응력 강도 계수(또는 파괴 강도)와 세 가지 모드의 응력 강도 계수를 연관시키는 파괴 기준이다. 이 고장 기준은 다음과[8]
K c 2 = K I 2 + K I I 2 + E ′ 2 μ K I I I 2 {\displaystyle K_{\rm{c}^{2}=K_{\rm{I}^{2}+K_{\rm {} II}^{2}+{\frac {E'}{2\mu }}}}\,K_{\rm{II}^{2}} 여기서 K c {\ displaystyle K_{\rm {c}} E ′ E 1 ν {\displaystyle '=E/(1-\nu ^{2}) 평면 스트레스 의 경우E ′ E {\displaystystyle '=E} 평면 스트레스 에 대한 임계 응력 강도 계수는 흔히 c {\ displaystyle K_{\rm{c}} .
예 무한 플레이트: 균일 단축 응력 무한영역의 페니모양 균열 유한판: 균일 단축 응력 균열이 폭 2 b [\displaystyle 2b} 2 h [\displaystyle 2h} ,
K I = σ π a [ 1 − a 2 b + 0.326 ( a b ) 2 1 − a b ] . {\displaystyle K_{\rm {I}}=\sigma {\sqrt {\pi a}}\left[{\cfrac {1-{\frac {a}{2b}}+0.326\left({\frac {a}{b}}\right)^{2}}{\sqrt {1-{\frac {a}{b}}}}}\right]\,. } 균열이 너비 d ≠ {\displaystyle d\neq b}), A 의 응력 강도 계수는 직렬 확장에[7] [9] .
K I A = σ π a [ 1 + ∑ n = 2 M C n ( a b ) n ] {\displaystyle K_{\rm { IA}}=\sigma {\pi a}\좌측[1+\sum _{n=2}^{M}C_{n}\좌측({\frac {a}{b}\우측) ^{n}\right]} 여기 Cn {\ displaystyle C_{n} displaystyle d} [7] : 6 , B 에 대해 유사한(동일하지는 않지만) 식을 찾을 수 있다. A 와 B 의 응력 강도 인자에 대한 대체 표현은 다음과 같다.
K I A = σ π a Φ A , K I B = σ π a Φ B {\displaystyle K_{\rm { IA}}=\sigma {\sqrt {\pi a}\,\Phi _{A}\,\rm {IB}}=\sigma {\sqrt {\pi a}\,\Phi _{B}}}}} 어디에
Φ A := [ β + ( 1 − β 4 ) ( 1 + 1 4 초 α A ) 2 ] 초 α A Φ B := 1 + [ 초 α A B − 1 1 + 0.21 죄를 짓다 { 8 햇볕에 그을리다 − 1 [ ( α A − α B α A + α B ) 0.9 ] } ] 디스플레이 스타일 {\displaystyle}\ Phi _{A}&:=\left[\beta +\left({\frac {1-\beta }{4}}\right)\left(1+{\frac {1}{4{\sqrt {\sec \alpha _{A}}}}}\right)^{2}\right]{\sqrt {\sec \alpha _{A}}}\\\Phi _{B}&:=1+\left[{\frac {{\sqrt {\sec \alpha _{AB}}}-1}{1+0.21\sin \left\{8\,\tan ^{-1}\left[\left({\frac {\alpha _{A}-\alpha _{B}}{\alpha _{A}+\alpha _{B}}}\right)^{0. 9}\오른쪽]\오른쪽\}\오른쪽]\끝{정렬}}} 와 함께
β := 죄를 짓다 ( π α B α A + α B ) , α A := π a 2 d , α B := π a 4 b − 2 d ; α A B := 4 7 α A + 3 7 α B . {\displaystyle \beta :=\sin \left({\frac \pi \alpha _{B}}}\alpha _{A}+\alpha _{B}\right)~~~,~~\frac {\pi a}{2d},~~ 알파 _{B: ={\frac {\pi a}{4b-2d}~~\alpha _{AB}={\frac {4}{7}\,\alpha _{A}+{3}}}\frac _{B}\, \alpha _{B}\, } 위의 표현에서 d {\displaystyle d} 지점 에 가장 가까운 경계까지의 거리입니다 d b {\displaystyle d=b} 단순화 되지 않는다는 점에 유의하십시오.
단축 응력 하에서 플레이트의 가장자리 균열 무한 플레이트: 이축 응력장 내 기울어진 균열 평면 내력 하에서의 플레이트 균열 길이 2 a {\displaystyle 2a} 2 × b {\displaystyle 2a} . x {\ displaystyle F_{x} F displaystystyle F_{y }} x, {\displaysty
판이 위치가 상대적 가까운 , 즉, 판 무한대 간주 있다. 이 경우 균열 팁 B 에서 F x {\ displaystyle F_{x}} x {\displaystyle x=a
K I = F x 2 π a ( κ − 1 κ + 1 ) [ G 1 + 1 κ − 1 H 1 ] K I I = F x 2 π a [ G 2 + 1 κ + 1 H 2 ] {\displaystyle {\begin{aligned}K_{\rm {I}}&={\frac {F_{x}}{2{\sqrt {\pi a}}}}\left({\frac {\kappa -1}{\kappa +1}}\right)\left[G_{1}+{\frac {1}{\kappa -1}}H_{1}\right]\ \K_{\rm { II}}&={\frac{F_{x}}{2{\\sqrt{\pi a}}}}}}\왼쪽[G_{2}+{\frac {1}{\appa +1}}}}}} H_{2}\오른쪽]\end{aigned}} 어디에
G 1 = 1 − 레 [ a + z z 2 − a 2 ] , G 2 = − 임 [ a + z z 2 − a 2 ] H 1 = 레 [ a ( z ¯ − z ) ( z ¯ − a ) z ¯ 2 − a 2 ] , H 2 = − 임 [ a ( z ¯ − z ) ( z ¯ − a ) z ¯ 2 − a 2 ] {\displaystyle {\reasoned} G_{1}&=1-{\text{Re}}\left[{\frac {a+z}{\sqrt {z^{2}-a^{2}}}}\right]\,,\,\,G_{2}=-{\text{Im}}\left[{\frac {a+z}{\sqrt {z^{2}-a^{2}}}}\right]\ \H_{1}&={\text{Re}}\left[{\frac {a({\bar {z}}-z)}{({\bar {z}}-a){\sqrt {{\bar {z}}^{2}-a^{2}}}}}\right]\,,\,\,H_{2}=-{\text{Im}}\left[{\frac {a({\bar {z}}-z)}{({\bar {z}}-a){\sqrt {{\bar {z}}^{2}-a^{2}}}}}\right]\end{aligned}}} with z = x + i y {\displaystyle z=x+iy} z ¯ = x − i y {\displaystyle {\bar {z}}=x-iy} κ = 3 − 4 ν {\displaystyle \kappa =3-4\nu } plane strain , κ = ( 3 − ν ) / ( 1 + ν ) {\displaystyle \kappa =(3-\nu )/(1+\nu )} plane stress , and ν {\displaystyle \nu } Poisson's ratio . 팁 B 의F y {\ displaystyle F_{y}
K I = F y 2 π a [ G 2 − 1 κ + 1 H 2 ] K I I = − F y 2 π a ( κ − 1 κ + 1 ) [ G 1 − 1 κ − 1 H 1 ] . {\displaystyle{\begin}K_{\rm{I}&={\frac{F_{F_{pi a}}}{2}\좌측[G_{2}-{1}{\frac{1}{\cappa +1}}}}}} H_{2}\오른쪽]\ \K_{\rm { II}}&=-{\frac{F_{y}}{2{\\sqrt{\pi a}}}}}\좌측({\fract {\cappa -1}{\cappa +1}\우측)\좌측[G_{1}-{\frappa -1}-{\1}{\H_{1}}\1}\우측],\우측],. \end{정렬}}} 팁 A (x {\displaystyle x=-a} 위치 (x y displaystyle { x}} ,
K I ( − a ; x , y ) = − K I ( a ; − x , y ) , K I I ( − a ; x , y ) = K I I ( a ; − x , y ) . {\displaystyle K_{\a;x,y}=-K_{\rm {I}}(a;-x,y)\\\,\,K_{\rm {II}(-a;x,y)=K_{\rm {II}(a;x,y)\, .} 마찬가지로 로드 y displaystyle F_{y
K I ( − a ; x , y ) = K I ( a ; − x , y ) , K I I ( − a ; x , y ) = − K I I ( a ; − x , y ) . {\displaystyle K_{\a;x,y}=K_{\rm{{I}}}(-x,y)\\\, K_{\rm {II}(-a;x,y)={\rm {II}(a;-x,y)\, .} 구성 요소 F x {\ displaystyle F_{x} F y {\ displaystyle F_{y}} .
접시에 장전된 균열 균열이 y 0 {\displaystyle y=0 } a x {\displaystyle -a>에 F displaystyle F_{y} B 지점의 응력 강도 계수는 다음과[7] .
K I = F y 2 π a a + x a − x , K I I = − F x 2 π a ( κ − 1 κ + 1 ) . {\displaystyle K_{\rm{I}={\frac {F_{y}}{2}{\\pi a}}{{{\pi}}}{\frac {a+x}}}\,\, K_{\rm {}}} II}}=-{\frac {{F_{x}}{2{\\sqrt{\pi a}}}}}\왼쪽({\frac {\cappa -1}{\cappa +1}\오른쪽)\, } 힘 x {\displaystyle -a<a 팁 B의 응력 강도 계수는 다음과 같다.
K I = 1 2 π a ∫ − a a F y ( x ) a + x a − x d x , K I I = − 1 2 π a ( κ − 1 κ + 1 ) ∫ − a a F y ( x ) d x , . {\displaystyle K_{\rm {I}={\frac {1}{2{\\sqrt{\pi a}}}\int _{-a}^{a}} F_{y}(x)\,{\sqrt {a+x}{a-x}}\,{\rm {d}x\,\,K_{\rm} II}}=-{\frac{1}{2{\\sqrt{\pi a}}}}\왼쪽({\frac {\cappa -1}{\cappa +1}\오른쪽)\int_{-a}^{a} F_{y}(x)\,{\rm {d}x,\, }
콤팩트 장력 시료 단일 모서리 노치 휨 시료 참고 항목 참조 ^ a b Anderson, T. L. (2005). Fracture mechanics: fundamentals and applications . CRC Press. ^ Soboyejo, W. O. (2003). "11.6.2 Crack Driving Force and Concept of Similitude". Mechanical properties of engineered materials ISBN 0-8247-8900-8 OCLC 300921090 . ^ Janssen, M. (Michael) (2004). Fracture mechanics ISBN 0-203-59686-2 OCLC 57491375 . ^ Hiroshi Tada ; P. C. Paris ; George R. Irwin (February 2000). The Stress Analysis of Cracks Handbook (3rd ed.). American Society of Mechanical Engineers.^ a b c Liu, M.; et al. (2015). "An improved semi-analytical solution for stress at round-tip notches" (PDF) . Engineering Fracture Mechanics . 149 : 134–143. ^ a b Suresh, S. (2004). Fatigue of Materials . Cambridge University Press. ISBN 978-0-521-57046-6 ^ a b c d e f g Rooke, D. P.; Cartwright, D. J. (1976). Compendium of stress intensity factors . HMSO Ministry of Defence. Procurement Executive. ^ Sih, G. C.; Macdonald, B. (1974), "Fracture mechanics applied to engineering problems-strain energy density fracture criterion", Engineering Fracture Mechanics , 6 (2): 361–386, doi :10.1016/0013-7944(74)90033-2 ^ 이시다, M, 1966, 편심 균열된 스트립의 장력에 대한 응력 강도 계수 , ASME 적용 역학 섹션의 거래, v. 88, p.94. ^ Kathiresan, K.; Brussat, T. R.; Hsu, T. M. (1984). Advanced life analysis methods. Crack Growth Analysis Methods for Attachment Lugs . Flight Dynamics Laboratory, Air Force Wright Aeronautical Laboratories, AFSC W-P Air Force Base, Ohio. ^ a b Sih, G. C.; Paris, P. C. & Erdogan, F. (1962), "Crack-tip stress intensity factors for the plane extension and plate bending problem", Journal of Applied Mechanics , 29 : 306–312, Bibcode :1962JAM....29..306S , doi :10.1115/1.3640546 ^ Erdogan, F. (1962), "On the stress distribution in plates with collinear cuts under arbitrary loads", Proceedings of the Fourth US National Congress of Applied Mechanics , 1 : 547–574 ^ a b Bower, A. F. (2009). Applied mechanics of solids . CRC Press.
외부 링크 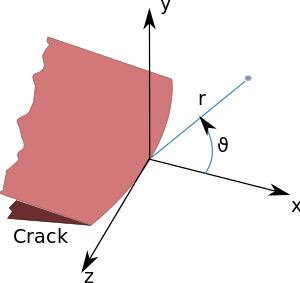


 균열 길이의 시료 기하학 종속 함수,
균열 길이의 시료 기하학 종속 함수, 


















![{\displaystyle \left\{{\begin{aligned}u_{x}\\u_{y}\end{aligned}}\right\}={\frac {K_{\rm {I}}}{2E}}{\sqrt {\frac {r}{2\pi }}}\left\{{\begin{aligned}(1+\nu )\left[(2\kappa -1)\cos {\frac {\theta }{2}}-\cos {\frac {3\theta }{2}}\right]\\(1+\nu )\left[(2\kappa +1)\sin {\frac {\theta }{2}}-\sin {\frac {3\theta }{2}}\right]\end{aligned}}\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f0e25b45c681a87a29ae2bf742923a7939601ec)
![{\displaystyle \left\{{\begin{aligned}u_{r}\\u_{\theta }\end{aligned}}\right\}={\frac {K_{\rm {I}}}{2E}}{\sqrt {\frac {r}{2\pi }}}\left\{{\begin{aligned}(1+\nu )\left[(2\kappa -1)\cos {\frac {\theta }{2}}-\cos {\frac {3\theta }{2}}\right]\\(1+\nu )\left[-(2\kappa +1)\sin {\frac {\theta }{2}}+\sin {\frac {3\theta }{2}}\right]\end{aligned}}\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2877b9da2e423a9465b1ecf02ca8ba8228b88c4a)









![{\displaystyle \left\{{\begin{aligned}u_{x}\\u_{y}\end{aligned}}\right\}={\frac {K_{\rm {II}}}{2E}}{\sqrt {\frac {r}{2\pi }}}\left\{{\begin{aligned}(1+\nu )\left[(2\kappa +3)\sin {\frac {\theta }{2}}+\sin {\frac {3\theta }{2}}\right]\\-(1+\nu )\left[(2\kappa -3)\cos {\frac {\theta }{2}}+\cos {\frac {3\theta }{2}}\right]\end{aligned}}\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38ef402da0c84b331d381c44a1ea1707e71a2518)
![{\displaystyle \left\{{\begin{aligned}u_{r}\\u_{\theta }\end{aligned}}\right\}={\frac {K_{\rm {II}}}{2E}}{\sqrt {\frac {r}{2\pi }}}\left\{{\begin{aligned}(1+\nu )\left[-(2\kappa -1)\sin {\frac {\theta }{2}}+3\sin {\frac {3\theta }{2}}\right]\\(1+\nu )\left[-(2\kappa +1)\cos {\frac {\theta }{2}}+3\cos {\frac {3\theta }{2}}\right]\end{aligned}}\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2da73f4a50588bd21c7a43fb7890366b8bec9b81)









 재료의
재료의 


 (는)
(는) 





 (는) 골절강성이며,
(는) 골절강성이며, 








![K_{{{\rm {I}}}}=\sigma {\sqrt {\pi a}}\left[{\cfrac {1-{\frac {a}{2b}}+0.326\left({\frac {a}{b}}\right)^{2}}{{\sqrt {1-{\frac {a}{b}}}}}}\right]\,.](https://wikimedia.org/api/rest_v1/media/math/render/svg/25cc4dadb6371c8239b7ebca823e25b13d2ffeb3)

![K_{{{\rm {IA}}}}=\sigma {\sqrt {\pi a}}\left[1+\sum _{{n=2}}^{{M}}C_{n}\left({\frac {a}{b}}\right)^{n}\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/71eaed2d5214af8609ee2614e072a831dff9bb27)



![{\begin{aligned}\Phi _{A}&:=\left[\beta +\left({\frac {1-\beta }{4}}\right)\left(1+{\frac {1}{4{\sqrt {\sec \alpha _{A}}}}}\right)^{2}\right]{\sqrt {\sec \alpha _{A}}}\\\Phi _{B}&:=1+\left[{\frac {{\sqrt {\sec \alpha _{{AB}}}}-1}{1+0.21\sin \left\{8\,\tan ^{{-1}}\left[\left({\frac {\alpha _{A}-\alpha _{B}}{\alpha _{A}+\alpha _{B}}}\right)^{{0.9}}\right]\right\}}}\right]\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97a81ceb7c9a5bbd82590c76afd49d6690a9c74a)






![{\displaystyle K_{\rm {I}}=\sigma {\sqrt {\pi a}}\left[1.122-0.231\left({\frac {a}{b}}\right)+10.55\left({\frac {a}{b}}\right)^{2}-21.71\left({\frac {a}{b}}\right)^{3}+30.382\left({\frac {a}{b}}\right)^{4}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d8ceaef43b7ab34b12662c8847e580f260cb701)


![K_{{{\rm {I}}}}=\sigma {\sqrt {\pi a}}\left[{\frac {1+3{\frac {a}{b}}}{2{\sqrt {\pi {\frac {a}{b}}}}\left(1-{\frac {a}{b}}\right)^{{3/2}}}}\right]\,.](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7a0366ab9b177d5a2d15ce70349ef83e9456f1f)





 (는)
(는) 








![{\begin{aligned}K_{{{\rm {I}}}}&={\frac {F_{x}}{2{\sqrt {\pi a}}}}\left({\frac {\kappa -1}{\kappa +1}}\right)\left[G_{1}+{\frac {1}{\kappa -1}}H_{1}\right]\\K_{{{\rm {II}}}}&={\frac {F_{x}}{2{\sqrt {\pi a}}}}\left[G_{2}+{\frac {1}{\kappa +1}}H_{2}\right]\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9df6165ba8ba56686979fe76299274dd25540945)
![{\begin{aligned}G_{1}&=1-{\text{Re}}\left[{\frac {a+z}{{\sqrt {z^{2}-a^{2}}}}}\right]\,,\,\,G_{2}=-{\text{Im}}\left[{\frac {a+z}{{\sqrt {z^{2}-a^{2}}}}}\right]\\H_{1}&={\text{Re}}\left[{\frac {a({\bar {z}}-z)}{({\bar {z}}-a){\sqrt {{{\bar {z}}}^{2}-a^{2}}}}}\right]\,,\,\,H_{2}=-{\text{Im}}\left[{\frac {a({\bar {z}}-z)}{({\bar {z}}-a){\sqrt {{{\bar {z}}}^{2}-a^{2}}}}}\right]\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0255e5aec3179e43fd82a04e723ef65dff683f6f)




![{\begin{aligned}K_{{{\rm {I}}}}&={\frac {F_{y}}{2{\sqrt {\pi a}}}}\left[G_{2}-{\frac {1}{\kappa +1}}H_{2}\right]\\K_{{{\rm {II}}}}&=-{\frac {F_{y}}{2{\sqrt {\pi a}}}}\left({\frac {\kappa -1}{\kappa +1}}\right)\left[G_{1}-{\frac {1}{\kappa -1}}H_{1}\right]\,.\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f91850cc6735cb02154d8d82ca2b502090d7a67)










![{\begin{aligned}K_{{{\rm {I}}}}&={\frac {P}{B}}{\sqrt {{\frac {\pi }{W}}}}\left[16.7\left({\frac {a}{W}}\right)^{{1/2}}-104.7\left({\frac {a}{W}}\right)^{{3/2}}+369.9\left({\frac {a}{W}}\right)^{{5/2}}\right.\\&\qquad \left.-573.8\left({\frac {a}{W}}\right)^{{7/2}}+360.5\left({\frac {a}{W}}\right)^{{9/2}}\right]\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a74d53e379ebf47cf3ea5f1a45619a1e78dcc4ad)
 (는) 적용 하중,
(는) 적용 하중,  (는) 시료의 두께,
(는) 시료의 두께, 
![{\begin{aligned}K_{{{\rm {I}}}}&={\frac {4P}{B}}{\sqrt {{\frac {\pi }{W}}}}\left[1.6\left({\frac {a}{W}}\right)^{{1/2}}-2.6\left({\frac {a}{W}}\right)^{{3/2}}+12.3\left({\frac {a}{W}}\right)^{{5/2}}\right.\\&\qquad \left.-21.2\left({\frac {a}{W}}\right)^{{7/2}}+21.8\left({\frac {a}{W}}\right)^{{9/2}}\right]\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/466d7f6e915a160e93963497a9016099b626cae6)



