스트립 패킹 문제

스트립 패킹 문제는 2차원 기하학적 최소화 문제다.축 정렬 직사각형 세트와 경계가 있는 폭과 무한 높이의 스트립이 주어진 경우 직사각형의 높이를 최소화하는 중첩되지 않은 패킹을 스트립으로 결정한다.이 문제는 절단 및 포장 문제로서 Waecher 외 연구진에 따르면 개방형 치수 문제로 분류된다.^[1]

이 문제는 일정 기간 동안 메모리의 연속적인 부분을 필요로 하는 작업을 모델링하는 스케줄링 영역에서 발생한다.또 다른 예는 산업 제조업 분야인데, 직사각형 조각은 가로는 고정되어 있지만 길이가 무한대인 한 장의 재료(예: 천이나 종이)에서 잘라내야 하며, 낭비되는 재료는 최소화하고자 한다.

이 문제는 1980년에 처음 연구되었다.^[2]그것은strongly-NP지 않는 한 P는 NP{P=NP\displaystyle}이 비율 3/2{3/2\displaystyle}보다 작게 다항 시간 근사 알고리즘이 존재한다. 그러나 가장 근접한 비율 지금까지( 검은 성주 하렌은(알에 의한 다항 시간 알고리즘에 의해 이루어진 어렵다.[3]cm는(5/3+ε){\displaystyle(5/3+\varepsil. $)}$ 에 $(5/3+\varepsilon )$ 근사 비율 $3/2$ / 2 $3/2$ 을(를) 가진 알고리즘이 있는지 여부를 묻는 공개 질문 $3/2$

정의

스트립 패킹 문제의 $I=({\mathcal {I}},W)$ I $I=({\mathcal {I}},W)$ = $I=({\mathcal {I}},W)$ ( $I=({\mathcal {I}},W)$ , $I=({\mathcal {I}},W)$ ) ${\displaystyle$ I $=({\mathcal {I},W)}$ 은 폭 $W=1$ = 1 $W=1$ 및 무한 높이의 $W=1$ 스트립과 직사각형 항목의 ${\mathcal {I}}$ I ${\$ { $I}$ 로 구성된다.Each item $i\in {\mathcal {I}}$ has a width $w_{i}\in (0,1]\cap \mathbb {Q}$ and a height $h_{i}\in (0,1]\cap \mathbb {Q}$ . A packing of the items is a mapping that maps each lower-left corner of an item $i\in {\mathcal {I}}$ $i\in {\mathcal {I}}$ to a position $(x_{i},y_{i})\in ([0,1-w_{i}]\cap \mathbb {Q} )\times \mathbb {Q} _{\geq 0}$ inside the strip.나의 집합에서 나는 ∈ 나는}{\displaystyle i\in{{나는\mathcal} 위치 항목의 내부의 점}은 지점 n(나는)){(), y)∈ Q×Q)나는 <^<>)나는 나는, y 나는 < w+, 베<>y 나는 + hi}{\displaystyle \mathrm{inn}(나는)=\{(x, y)\in \mathbb{Q}\times{Q}x_{나는}< \mathbb, x<, x_{나는}+w_{나는},y_{나는}<.;y<, y_{나는}+h_{나는}\}}. 내부 포인트를 공유하면 2개(위치) 항목이 겹친다.패킹의 높이는 $\max\{y_{i}+h_{i}|i\in {\mathcal {I}}\}$ { $\max\{y_{i}+h_{i}|i\in {\mathcal {I}}\}$ i + $\max\{y_{i}+h_{i}|i\in {\mathcal {I}}\}$ $\max\{y_{i}+h_{i}|i\in {\mathcal {I}}\}$ I $\max\{y_{i}+h_{i}|i\in {\mathcal {I}}\}$ {\ $displaystyle \max\{y_}+h_{$ i}+ $h_{i}$ i\ $in$ {\ $mathcal {I}\}}$ 으로 정의된다 $\max\{y_{i}+h_{i}|i\in {\mathcal {I}}\}$ 포장 높이를 최소화하면서 스트립 내부 물건의 겹치지 않는 패킹을 찾는 것이 목적이다.

이 정의는 모든 다항 시간 알고리즘에 사용된다.의사-폴리놈 시간 및 FPT-알고리즘의 경우 표기법 단순화를 위해 정의가 약간 변경된다.이 경우 나타나는 모든 크기는 필수적이다.특히 스트립의 너비는 1보다 큰 임의의 정수 숫자로 주어진다.이 두 정의는 동일하다는 점에 유의하십시오.

변형

스트립 패킹 문제는 여러 가지 변종이 연구되어 왔다.이러한 변형은 물체의 기하학적 구조, 문제의 크기, 품목을 회전할 수 있는 경우 및 포장 구조와 관련이 있다.^[4]

항목의 지오메트리:이 문제의 표준 변종에서 주어진 항목 세트는 직사각형으로 구성된다.종종 고려되는 하위 사례에서 모든 항목은 정사각형이어야 한다.이 변종은 이미 스트립 패킹에 대한 첫 번째 논문에서 고려되었다.^[2]또한 모양이 원형 또는 심지어 불규칙한 곳에 변형이 연구되었다.후자의 경우, 우리는 불규칙한 스트립 패킹에 대해 말한다.

치수:다르게 언급되지 않았을 때 스트립 패킹 문제는 2차원 문제다.그러나, 그것은 또한 3차원 혹은 더 많은 차원으로 연구되어 왔다.이 경우 물체는 초직각이며, 스트립은 한 차원 개방되고 나머지 차원에 경계된다.

회전:고전적인 스트립 패킹 문제에서는 아이템을 회전시킬 수 없다.그러나 90도 회전이 허용되거나 임의의 각도가 허용되는 경우 변형이 연구되었다.

패킹 구조:일반적인 스트립 패킹 문제에서 패킹의 구조는 무관하다.단, 패킹 구조에 관한 명시적 요건이 있는 어플리케이션도 있다.이 요건들 중 하나는 수평 또는 수직 가장자리부터 가장자리 절단까지 스트립에서 항목을 절단할 수 있어야 한다.이런 종류의 절단을 허용하는 패킹을 기요틴 패킹이라고 한다.

경도

스트립 패킹 문제는 모든 품목이 동일한 높이 1을 가질 때 특별한 경우로서 빈 패킹 문제를 포함한다.For this reason, it is strongly NP-hard and there can be no polynomial time approximation algorithm, which has an approximation ratio smaller than $3/2$ unless $P=NP$ . Furthermore, unless $P=NP$ , there cannot be a pseudo-polynomial time algorithm that has a강력한 NP-완전 3파티션 문제의 감소로 증명할 수 있는 $5/4$ ^[5] $/$ 4 $보다$ 작은 n 근사 비율.항목을 90도 회전할 수 있는 경우에도 하한 $3/2$ / $3/2$ $3/2$ 및 $3/2$ $5/4$ / $5/4$ $5/4$ 을 $5/4$ (를) 유지하십시오.또한,^[6] 스트립 패킹은 최적 패킹 높이에 의해 매개변수화되었을 때 W[1]-hard라는 것이 Ashok 외 연구진에 의해 입증되었다.

최적 솔루션의 속성

최적의 해결책에는 두 가지 사소한 하한선이 있다.첫 번째는 가장 큰 아이템의 높이다. $h_{\max }(I):=\max\{h(i)|i\in {\mathcal {I}}\}$ $h_{\max }(I):=\max\{h(i)|i\in {\mathcal {I}}\}$ ( $h_{\max }(I):=\max\{h(i)|i\in {\mathcal {I}}\}$ ) $h_{\max }(I):=\max\{h(i)|i\in {\mathcal {I}}\}$ $h_{\max }(I):=\max\{h(i)|i\in {\mathcal {I}}\}$ { $h_{\max }(I):=\max\{h(i)|i\in {\mathcal {I}}\}$ ( $h_{\max }(I):=\max\{h(i)|i\in {\mathcal {I}}\}$ ) $h_{\max }(I):=\max\{h(i)|i\in {\mathcal {I}}\}$ $h_{\max }(I):=\max\{h(i)|i\in {\mathcal {I}}\}$ $h_{\max }(I):=\max\{h(i)|i\in {\mathcal {I}}\}$ } ${\displaystyle h_{\max }(I):$ $=\max\{h(i)$ i $\in {\mathcal{I$ 그리고 그것은 그것을 지탱한다.

$OPT(I)\geq h_{\max }(I)$ $OPT(I)\geq h_{\max }(I)$ $OPT(I)\geq h_{\max }(I)$ ( $OPT(I)\geq h_{\max }(I)$ ) $OPT(I)\geq h_{\max }(I)$ h $OPT(I)\geq h_{\max }(I)$ ( $OPT(I)\geq h_{\max }(I)$ ) ${\displaystyle OPT(I)\geq h_{\max }(I$

또 다른 하한은 항목의 전체 면적에 의해 주어진다. $\mathrm {AREA} ({\mathcal {I}}):=\sum _{i\in {\mathcal {I}}}h(i)w(i)$ $\mathrm {AREA} ({\mathcal {I}}):=\sum _{i\in {\mathcal {I}}}h(i)w(i)$ $\mathrm {AREA} ({\mathcal {I}}):=\sum _{i\in {\mathcal {I}}}h(i)w(i)$ $\mathrm {AREA} ({\mathcal {I}}):=\sum _{i\in {\mathcal {I}}}h(i)w(i)$ ( $\mathrm {AREA} ({\mathcal {I}}):=\sum _{i\in {\mathcal {I}}}h(i)w(i)$ ) $\mathrm {AREA} ({\mathcal {I}}):=\sum _{i\in {\mathcal {I}}}h(i)w(i)$ $\mathrm {AREA} ({\mathcal {I}}):=\sum _{i\in {\mathcal {I}}}h(i)w(i)$ $\mathrm {AREA} ({\mathcal {I}}):=\sum _{i\in {\mathcal {I}}}h(i)w(i)$ $\mathrm {AREA} ({\mathcal {I}}):=\sum _{i\in {\mathcal {I}}}h(i)w(i)$ I $\mathrm {AREA} ({\mathcal {I}}):=\sum _{i\in {\mathcal {I}}}h(i)w(i)$ ( $\mathrm {AREA} ({\mathcal {I}}):=\sum _{i\in {\mathcal {I}}}h(i)w(i)$ ) $\mathrm {AREA} ({\mathcal {I}}):=\sum _{i\in {\mathcal {I}}}h(i)w(i)$ w {\ $displaystyle \mathrm {ARIA}({\mathcal {I}):$ $=\sum _{i\in {\mathcal{I}}h(i)w(i)}$ 그러면 $\mathrm {AREA} ({\mathcal {I}}):=\sum _{i\in {\mathcal {I}}}h(i)w(i)$ 이 값이 유지된다.

$OPT(I)\geq \mathrm {AREA} ({\mathcal {I}})/W$ $OPT(I)\geq \mathrm {AREA} ({\mathcal {I}})/W$ T $OPT(I)\geq \mathrm {AREA} ({\mathcal {I}})/W$ ( I $OPT(I)\geq \mathrm {AREA} ({\mathcal {I}})/W$ ) $OPT(I)\geq \mathrm {AREA} ({\mathcal {I}})/W$ $OPT(I)\geq \mathrm {AREA} ({\mathcal {I}})/W$ R $OPT(I)\geq \mathrm {AREA} ({\mathcal {I}})/W$ $OPT(I)\geq \mathrm {AREA} ({\mathcal {I}})/W$ ( $OPT(I)\geq \mathrm {AREA} ({\mathcal {I}})/W$ ) $OPT(I)\geq \mathrm {AREA} ({\mathcal {I}})/W$ / $OPT(I)\geq \mathrm {AREA} ({\mathcal {I}})/W$ ${\displaystyle OPT(I)\geq \mathrm {ARIA}({\mathcal {I})/W$ .

다음의 두 가지 하한은 특정 품목을 스트립에서 서로 옆에 배치할 수 없다는 사실에 주목하며, ${\mathcal {O}}(n\log(n))$ ${\mathcal {O}}(n\log(n))$ ${\mathcal {O}}(n\log(n))$ $){\displaystyle{\mathcal{O}}(n\log(n))})$ 로 계산할 수 있다 ${\mathcal {O}}(n\log(n))$ ^[7] 첫 번째 하한은 품목은 비상승 높이에 의해 정렬된다고 가정한다.Define $k:=\max\{i:\sum _{j=1}^{k}w(j)\leq W\}$ . For each $l>k$ define $i(l)\leq k$ the first index such that ${\displaystyle w(l)+\sum _{j=1}^{i(l)}w(j)>$ $W}$ 그렇다면 그것은 지탱하고 있다 $w(l)+\sum _{j=1}^{i(l)}w(j)>W$

${\displaystyle OPT(I)\geq \max\{h(l)+h(i(l)) l>k\wedge w(l)+\sum _{j=1}^{i(l)}w(j)>$ $W$ ^[7]

두 번째 하한에 대해서는 항목 집합을 세 집합으로 분할하십시오. $\alpha \in [1,W/2]\cap \mathbb {N}$ $\alpha \in [1,W/2]\cap \mathbb {N}$ [ $\alpha \in [1,W/2]\cap \mathbb {N}$ , $\alpha \in [1,W/2]\cap \mathbb {N}$ / $\alpha \in [1,W/2]\cap \mathbb {N}$ $\alpha \in [1,W/2]\cap \mathbb {N}$ $\alpha \in [1,W/2]\cap \mathbb {N}$ $\alpha \in [1,W/2]\cap \mathbb {N}$ ${\$ 을(를) 자르고 $\alpha \in [1,W/2]\cap \mathbb {N}$ ${\mathcal {I}}_{1}(\alpha ):=\{i\in {\mathcal {I}}|w(i)>W-\alpha \}$ 1 ( ${\mathcal {I}}_{1}(\alpha ):=\{i\in {\mathcal {I}}|w(i)>W-\alpha \}$ ) ${\mathcal {I}}_{1}(\alpha ):=\{i\in {\mathcal {I}}|w(i)>W-\alpha \}$ { ${\mathcal {I}}_{1}(\alpha ):=\{i\in {\mathcal {I}}|w(i)>W-\alpha \}$ ∈ I ${\mathcal {I}}_{1}(\alpha ):=\{i\in {\mathcal {I}}|w(i)>W-\alpha \}$ ( ${\mathcal {I}}_{1}(\alpha ):=\{i\in {\mathcal {I}}|w(i)>W-\alpha \}$ ) ${\mathcal {I}}_{1}(\alpha ):=\{i\in {\mathcal {I}}|w(i)>W-\alpha \}$ > ${\mathcal {I}}_{1}(\alpha ):=\{i\in {\mathcal {I}}|w(i)>W-\alpha \}$ - ${\mathcal {I}}_{1}(\alpha ):=\{i\in {\mathcal {I}}|w(i)>W-\alpha \}$ ${\mathcal {I}}_{1}(\alpha ):=\{i\in {\mathcal {I}}|w(i)>W-\alpha \}$ ${\displaystyle$ { $I}{1}(\mathcalpha }).$ $=\{i\in {\mathcal {I}w(i)$ $W-\alpha$ ${\mathcal {I}}_{1}(\alpha ):=\{i\in {\mathcal {I}}|w(i)>W-\alpha \}$ ${\mathcal {I}}_{2}(\alpha ):=\{i\in {\mathcal {I}}|W-\alpha \geq w(i)>W/2\}$ ${\mathcal {I}}_{2}(\alpha ):=\{i\in {\mathcal {I}}|W-\alpha \geq w(i)>W/2\}$ ( ${\mathcal {I}}_{2}(\alpha ):=\{i\in {\mathcal {I}}|W-\alpha \geq w(i)>W/2\}$ ) ${\mathcal {I}}_{2}(\alpha ):=\{i\in {\mathcal {I}}|W-\alpha \geq w(i)>W/2\}$ { I ${\mathcal {I}}_{2}(\alpha ):=\{i\in {\mathcal {I}}|W-\alpha \geq w(i)>W/2\}$ ${\mathcal {I}}_{2}(\alpha ):=\{i\in {\mathcal {I}}|W-\alpha \geq w(i)>W/2\}$ ${\mathcal {I}}_{2}(\alpha ):=\{i\in {\mathcal {I}}|W-\alpha \geq w(i)>W/2\}$ - ${\mathcal {I}}_{2}(\alpha ):=\{i\in {\mathcal {I}}|W-\alpha \geq w(i)>W/2\}$ α ${\mathcal {I}}_{2}(\alpha ):=\{i\in {\mathcal {I}}|W-\alpha \geq w(i)>W/2\}$ ( ${\mathcal {I}}_{2}(\alpha ):=\{i\in {\mathcal {I}}|W-\alpha \geq w(i)>W/2\}$ ) ${\mathcal {I}}_{2}(\alpha ):=\{i\in {\mathcal {I}}|W-\alpha \geq w(i)>W/2\}$ > W ${\mathcal {I}}_{2}(\alpha ):=\{i\in {\mathcal {I}}|W-\alpha \geq w(i)>W/2\}$ / ${\mathcal {I}}_{2}(\alpha ):=\{i\in {\mathcal {I}}|W-\alpha \geq w(i)>W/2\}$ ${\displaystyle {\mathcal {I}_{2}(\alpha ):$ $=\{i\in {\mathcal {I}W-\alpha \geq w(i)$ $W/2\},$ 및 ${\mathcal {I}}_{3}(\alpha ):=\{i\in {\mathcal {I}}|W/2\geq w(i)>\alpha \}$ ${\mathcal {I}}_{3}(\alpha ):=\{i\in {\mathcal {I}}|W/2\geq w(i)>\alpha \}$ ${\mathcal {I}}_{3}(\alpha ):=\{i\in {\mathcal {I}}|W/2\geq w(i)>\alpha \}$ ) ${\mathcal {I}}_{3}(\alpha ):=\{i\in {\mathcal {I}}|W/2\geq w(i)>\alpha \}$ { ${\mathcal {I}}_{3}(\alpha ):=\{i\in {\mathcal {I}}|W/2\geq w(i)>\alpha \}$ ${\mathcal {I}}_{3}(\alpha ):=\{i\in {\mathcal {I}}|W/2\geq w(i)>\alpha \}$ ${\mathcal {I}}_{3}(\alpha ):=\{i\in {\mathcal {I}}|W/2\geq w(i)>\alpha \}$ W ${\mathcal {I}}_{3}(\alpha ):=\{i\in {\mathcal {I}}|W/2\geq w(i)>\alpha \}$ / ${\mathcal {I}}_{3}(\alpha ):=\{i\in {\mathcal {I}}|W/2\geq w(i)>\alpha \}$ ≥ ${\mathcal {I}}_{3}(\alpha ):=\{i\in {\mathcal {I}}|W/2\geq w(i)>\alpha \}$ ( ${\mathcal {I}}_{3}(\alpha ):=\{i\in {\mathcal {I}}|W/2\geq w(i)>\alpha \}$ ) > ${\mathcal {I}}_{3}(\alpha ):=\{i\in {\mathcal {I}}|W/2\geq w(i)>\alpha \}$ ${\mathcal {I}}_{3}(\alpha ):=\{i\in {\mathcal {I}}|W/2\geq w(i)>\alpha \}$ ${\displaystyle {\mathcal {I}_{3}(\alpha ):$ $=\{i\in {\mathcal {I}W/2\geq$ w $(i)>\alpha$ 그러면 이 값이 고정된다.

${\displaystyle OPT(I)\geq \max _{\alpha \in [1,W/2]\cap \mathbb {N} }{\Bigg \{}\sum _{i\in {\mathcal {I}}_{1}($ $\alpha )\cup {\mathcal {I}}_{2}(\alpha )}h(i)+\left({\frac {\sum _{i\in {\mathcal {I}}_{3}(\alpha )h(i)w(i)-\sum _{i\in {\mathcal {I}}_{2}(\alpha )}(W-w(i))h(i)}}{$ $W}}\오른쪽)_{{+}{\$ $(x)_{+}:=\max\{x,0\}$ $OPT(I)\geq \max _{\alpha \in [1,W/2]\cap \mathbb {N} }{\Bigg \{}\sum _{i\in {\mathcal {I}}_{1}(\alpha )\cup {\mathcal {I}}_{2}(\alpha )}h(i)+\left({\frac {\sum _{i\in {\mathcal {I}}_{3}(\alpha )h(i)w(i)-\sum _{i\in {\mathcal {I}}_{2}(\alpha )}(W-w(i))h(i)}}{W}}\right)_{+}{\Bigg \}}$ ^[7] 여기서 ( x $(x)_{+}:=\max\{x,0\}$ ) $(x)_{+}:=\max\{x,0\}$ + : $(x)_{+}:=\max\{x,0\}$ = $(x)_{+}:=\max\{x,0\}$ { $(x)_{+}:=\max\{x,0\}$ $(x)_{+}:=\max\{x,0\}$ $(x)_{+}:=\max\{x,0\}$ $(x)_{+}:=\max\{x,0\}$ $x\in \mathbb {R}$ x $(x)_{+}:=\max\{x,0\}$ $x\in \mathbb {R}$ $x\in \mathbb {R}$ ${\$

반면 스타인버그는^[8] 최적의 용액의 높이가 다음과 같이 상한선을 둘 수 있음을 보여 주었다.

$OPT(I)\leq 2\max\{h_{\max }(I),\mathrm {AREA}({\mathcal {I})/W\}$

More precisely he showed that given a $W\geq w_{\max }({\mathcal {I}})$ and a $H\geq h_{\max }(I)$ then the items ${\mathcal {I}}$ can be placed inside a box with width $W$ and height $H$ $H$ 만일

$WH\geq 2\mathrm {AREA} ({\mathcal {I}})+(2w_{\max }({\mathcal {I}})-W)_{+}(2h_{\max }(I)-H)_{+}$ , where $(x)_{+}:=\max\{x,0\}$ .

다항 시간 근사 알고리즘

이 문제가 NP-hard이기 때문에 이 문제에 대한 근사 알고리즘이 연구되었다.대부분의 경험적 접근법은 $[\displaystyle 3}$ 과 $3$ 2 $[\displaystyle 2}$ 사이의 근사 비율을 가지고 있다 $2$ $[\displaystyle 2}$ 미만의 비율로 알고리즘을 찾는 것은 어려워 보이며 $2$ , 해당 알고리즘의 실행 시간과 설명에 있어 복잡성이 증가한다.지금까지 달성한 최소 근사비는 $(5/3+\varepsilon )$ ( $(5/3+\varepsilon )$ / $(5/3+\varepsilon )$ + $(5/3+\varepsilon )$ ) $(5/3+\varepsilon )$ 입니다 $(5/3+\varepsilon )$

다항식 시간 근사치 개요
연도	이름	근사보증	출처
1980	상향 왼쪽 정렬(BL)	$3OPT(I)$	베이커 ^[2]외
1980	넥스트핏 감소-높이(NFDH)	$2OPT(I)+h_{\max }(I)\leq 3OPT(I)$	커피만 ^[9]외
	퍼스트핏 감소-높이(FFDH)	$1.7 디스플레이 스타일OPT(I)+h_{\max }(I)\leq 2.7OPT(I)}$
	SF(Split-Fit)	$(\displaystyle 1.5)OPT(I)+2h_{\max }(I)}$
1980		$2OPT(I)+h_{\max }(I)/2\leq 2.5OPT(I)$	노예제^[10]
1981	분할 알고리즘(SP)	$3OPT(I)$	골란^[11]
1981	혼성알고릿옴	$(4/3)OPT(I)+7{\frac {1}{18}h_{\max }(I)$	골란^[11]
1981	업다운(UD)	$(5/4)OPT(I)+6{\frac {7}{8}h_{\max }(I)$	베이커 ^[12]외
1994	리버스핏	$2OPT(I)$	슈어마이어^[13]
1997		$2OPT(I)$	스타인버그^[8]
2000		$(1+\varepsilon )OPT(I)+{\mathcal {O}(1/\varepsilon ^{2}h_{\max }(I)}$	케년, 레밀라^[14]
2009		$1.9396OPT(I)$	하렌, 반 스티^[15]
2009		${\displaystyle(1+\varepsilon )OPT(I)+h_{\max }(I)}$	얀센, 솔리스오바^[16]
2011		$(1+\varepsilon )OPT(I)+{\mathcal {O}(\log(1/\varepsilon )/\varepsilon )h_{\max }(I)$	부게렛 ^[17]외
2012		$(1+\varepsilon )OPT(I)+{\mathcal {O}(\log(1/\varepsilon )/\varepsilon )h_{\max }(I)$	스비리덴코^[18]
2014		$[\displaystyle (5/3+\varepsilon )OPT(I)}$	하렌 ^[3]외

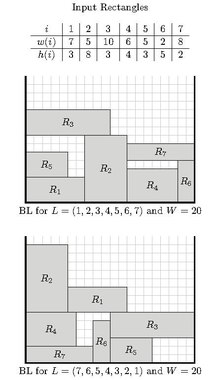
하단 위 왼쪽 정렬(BL)

Bottom-Up Left-Justified 알고리즘에 의해 생성된 솔루션의 예.

이 알고리즘은 베이커 외 연구진에 의해 처음 설명되었다.^[2]다음과 같이 작동한다.

$L$ $L$ 을(를) 직사각형 항목의 순서가 되도록 $L$ 한다.알고리즘은 주어진 순서에 따라 순서를 반복한다.고려된 각 항목 $r\in L$ $r\in L$ $r\in L$ $r\in L$ 에 대해 가장 아래 위치를 검색하여 배치한 다음 가능한 한 왼쪽으로 이동시킨다 $r\in L$ 따라서 가장 왼쪽 아래 좌표 $(x,y)$ , $(x,y)$ )에 $r$ $r$ ${\$ $displaystyle$ $r}$ 을(를 $)$ 배치한다 $(x,y)$ $.$

이 알고리즘에는 다음과 같은 속성이 있다.

이 알고리즘의 근사 비율은 상수로 경계를 지정할 수 없다.좀 더 정밀하게 그들은 각 M을, 0{\displaystyle M>0}이 장방형 항목의 목록을 나는{L\displaystyle}폭 증가하고 명령에 따라 존재하는지 보여 주는 것처럼 BL(L)/OPT(L)>M{\displaystyle BL(L)(L)&gt을 말한다.M}, 포장을 연사 alg을 통해 이 곳에서는 B나는(L){BL(L)\displaystyle}은 높이.Orithm 및 $OPT(L)$ $OPT(L)$ $OPT(L)$ ( L $OPT(L)$ ) $OPT(L)$ 은 $L$ $L$ 에 대한 최적 용액의 높이 입니다 $OPT(L)$ $L$ ^[2]
폭을 줄여 항목을 주문하는 경우, $BL(L)/OPT(L)\leq 3$ L $BL(L)/OPT(L)\leq 3$ ( $BL(L)/OPT(L)\leq 3$ ) $BL(L)/OPT(L)\leq 3$ / $BL(L)/OPT(L)\leq 3$ $BL(L)/OPT(L)\leq 3$ $BL(L)/OPT(L)\leq 3$ ( L $BL(L)/OPT(L)\leq 3$ ) $BL(L)/OPT(L)\leq 3$ $BL(L)/OPT(L)\leq 3$ $BL(L)/OPT(L)\leq 3$ ^[2].
품목이 모두 정사각형이고 폭을 줄여서 정렬된 경우, $BL(L)/OPT(L)\leq 2$ L $BL(L)/OPT(L)\leq 2$ ( $BL(L)/OPT(L)\leq 2$ L ) $BL(L)/OPT(L)\leq 2$ / $BL(L)/OPT(L)\leq 2$ P $BL(L)/OPT(L)\leq 2$ ( $BL(L)/OPT(L)\leq 2$ ) $BL(L)/OPT(L)\leq 2$ 2 ${\displaystyle BL(L)/OPT(L)\leq 2$ ^[2] .
$\delta >0$ > $\delta >0$ ${\displaystyle \delta$ > $0$ 에 대해, B $BL(L)/OPT(L)>3-\delta$ ( $BL(L)/OPT(L)>3-\delta$ ) $BL(L)/OPT(L)>3-\delta$ / $BL(L)/OPT(L)>3-\delta$ $BL(L)/OPT(L)>3-\delta$ $BL(L)/OPT(L)>3-\delta$ ( $BL(L)/OPT(L)>3-\delta$ ) $BL(L)/OPT(L)>3-\delta$ > $BL(L)/OPT(L)>3-\delta$ - $BL(L)/OPT(L)>3-\delta$ $BL(L)/OPT(L)3-\delta$ 과 같이 폭을 줄여서 주문한 직사각형 $L$ L ${\displaystyle$ L $}$ 이 존재한다 $BL(L)/OPT(L)>3-\delta$ ^[2]
$\delta >0$ > $\delta >0$ ${\displaystyle \delta >0$ 에 대해, B $BL(L)/OPT(L)>2-\delta$ ( $BL(L)/OPT(L)>2-\delta$ ) / $BL(L)/OPT(L)>2-\delta$ P $BL(L)/OPT(L)>2-\delta$ ( $BL(L)/OPT(L)>2-\delta$ ) > $BL(L)/OPT(L)>2-\delta$ - $BL(L)/OPT(L)>2-\delta$ {\ $displaystyle BL(L)/OPT(L)$ > $2-\delta$ }과 같이 폭을 줄여서 정렬된 $목록$ L ${\displaystystyle L}$ 이 $L$ 존재한다 $BL(L)/OPT(L)>2-\delta$ ^[2]
각 ε 들어(0,1]{\displaystyle \varepsilon \in(0,1 해결}, 인스턴스는 사각형 각각의 주문 나는 유일한 사각형이 포함된{\displaystyle L}BL의 비율이 나는 존재하)/OPT(L)>1211+ε{\displaystyle BL(L)(L)>,{\frac{12}{11+\varepsilon}}}, 즉, 연사 페니 사례 존재하 ∈없oes품목의 가능한 모든 주문을 반복해도 최적점을 찾지 못한다.^[2]

넥스트핏 감소 높이(NFDH)

동일한 인스턴스에 적용된 NFDH 및 FFDH의 예

이 알고리즘은 1980년 ^[9]Coffman 등이 처음 설명한 것으로 다음과 같이 동작한다.

${\mathcal {I}}$ ${\$ 을(를) 지정된 직사각형 항목 집합으로 설정하십시오 ${\mathcal {I}}$ .먼저 알고리즘은 높이를 높이지 않는 순서로 항목을 정렬한다.그런 다음 $(0,0)$ ( $(0,0)$ , 0 $(0,0)$ ) ${\displaystyle (0,0$ 위치에서 시작하여 다음 항목이 스트립의 오른쪽 테두리와 겹칠 때까지 알고리즘은 항목을 스트립에 서로 옆에 배치한다.이 시점에서 알고리즘은 현재 레벨에서 가장 높은 아이템의 상단에 새로운 레벨을 정의하고, 이 새로운 레벨에서 아이템을 서로 옆에 배치한다.

이 알고리즘에는 다음과 같은 속성이 있다.

실행 시간은 ${\mathcal {O}}(|{\mathcal {I}}|\log(|{\mathcal {I}}|))$ ${\mathcal {O}}(|{\mathcal {I}}|\log(|{\mathcal {I}}|))$ ${\mathcal {O}}(|{\mathcal {I}}|\log(|{\mathcal {I}}|))$ ( I $){\displaystyle {\mathcal {O}({\mathcal {I})}({\mathcal {I})$ 로 한정할 수 있으며, ${\mathcal {O}}(|{\mathcal {I}}|)$ 이 ${\mathcal {O}}(|{\mathcal {I}}|\log(|{\mathcal {I}}|))$ O $I$ 로 이미 정렬된 경우 ${\mathcal {O}}(|{\mathcal {I}}|)$
For every set of items ${\mathcal {I}}$ , it produces a packing of height $NFDH({\mathcal {I}})\leq 2OPT({\mathcal {I}})+h_{\max }\leq 3OPT({\mathcal {I}})$ , where $h_{\max }$ is the largest height o ${\mathcal {I}}$ ${\$ 의 항목 ${\mathcal {I}}$ ^[9]
For every $\varepsilon >0$ there exists a set of rectangles ${\mathcal {I}}$ such that ${\displaystyle NFDH({\mathcal {I}} )>(2-\varepsilon )OPT({\mathcal {I}}).$ $}$ ^[9]
생산되는 포장재는 단두대 포장이다.이는 항목들이 일련의 수평 또는 수직 가장자리 절단을 통해 얻을 수 있다는 것을 의미한다.

퍼스트핏 감소 높이(FFDH)

1980년 ^[9]Coffman 등이 처음 설명한 이 알고리즘은 NFDH 알고리즘과 유사하게 작동한다.그러나 다음 항목을 배치할 때 알고리즘은 아래부터 위까지 레벨을 스캔하여 항목이 들어갈 첫 번째 레벨에 배치한다.새로운 레벨은 그 아이템이 이전의 어떤 것과도 맞지 않는 경우에만 개방된다.

이 알고리즘에는 다음과 같은 속성이 있다.

실행 시간은 최대 $|{\mathcal {I}}|$ $displaystyle$ ${\mathcal {O$ $}({\mathcal$ ${I$ $}^{2$ $})$ 레벨이 있으므로 $|{\mathcal {I}}|$ ${\mathcal {O}}(|{\mathcal {I}}|^{2})$ 2)로 제한될 수 있다.
항목 ${\mathcal {I}}$ ${\$ $FFDH({\mathcal {I}})\leq 1.7OPT({\mathcal {I}})+h_{\max }\leq 2.7OPT({\mathcal {I}})$ $}}$ 의 모든 세트에 대해 ${\mathcal {I}}$ $FFDH({\mathcal {I}})\leq 1.7OPT({\mathcal {I}})+h_{\max }\leq 2.7OPT({\mathcal {I}})$ F $FFDH({\mathcal {I}})\leq 1.7OPT({\mathcal {I}})+h_{\max }\leq 2.7OPT({\mathcal {I}})$ D $FFDH({\mathcal {I}})\leq 1.7OPT({\mathcal {I}})+h_{\max }\leq 2.7OPT({\mathcal {I}})$ ( $FFDH({\mathcal {I}})\leq 1.7OPT({\mathcal {I}})+h_{\max }\leq 2.7OPT({\mathcal {I}})$ ) $FFDH({\mathcal {I}})\leq 1.7OPT({\mathcal {I}})+h_{\max }\leq 2.7OPT({\mathcal {I}})$ 1 $FFDH({\mathcal {I}})\leq 1.7OPT({\mathcal {I}})+h_{\max }\leq 2.7OPT({\mathcal {I}})$ $FFDH({\mathcal {I}})\leq 1.7OPT({\mathcal {I}})+h_{\max }\leq 2.7OPT({\mathcal {I}})$ $FFDH({\mathcal {I}})\leq 1.7OPT({\mathcal {I}})+h_{\max }\leq 2.7OPT({\mathcal {I}})$ $FFDH({\mathcal {I}})\leq 1.7OPT({\mathcal {I}})+h_{\max }\leq 2.7OPT({\mathcal {I}})$ ( I $FFDH({\mathcal {I}})\leq 1.7OPT({\mathcal {I}})+h_{\max }\leq 2.7OPT({\mathcal {I}})$ ) $FFDH({\mathcal {I}})\leq 1.7OPT({\mathcal {I}})+h_{\max }\leq 2.7OPT({\mathcal {I}})$ + h $FFDH({\mathcal {I}})\leq 1.7OPT({\mathcal {I}})+h_{\max }\leq 2.7OPT({\mathcal {I}})$ 2 $FFDH({\mathcal {I}})\leq 1.7OPT({\mathcal {I}})+h_{\max }\leq 2.7OPT({\mathcal {I}})$ O $FFDH({\mathcal {I}})\leq 1.7OPT({\mathcal {I}})+h_{\max }\leq 2.7OPT({\mathcal {I}})$ $FFDH({\mathcal {I}})\leq 1.7OPT({\mathcal {I}})+h_{\max }\leq 2.7OPT({\mathcal {I}})$ ( $){\displaysty FFDH({mathcal {I})\leq$ 1.7의 패킹을 생성한다 $.$ $OPT({\mathcal{I})+h_{\max }\leq$ $OPT({\mathcal{I$ 여기서 $h_{\max }$ $h_{\max }$ ${\$ 는 $h_{\max }$ ${\mathcal {I}}$ ${\$ 에서 항목의 가장 ${\mathcal {I}}$ ^[9]큰 높이 입니다.
Let $m\geq 2$ . For any set of items ${\mathcal {I}}$ and strip with width $W$ such that $w(i)\leq W/m$ for each $i\in {\mathcal {I}}$ , it holds that $FFDH({\mathcal {I}})\leq \left(1+1/m\right)OPT({\mathcal {I}})+h_{\max }$ ${\$ $OPT({\mathcal {I}})+h_{\max }}$ . Furthermore, for each $\varepsilon >0$ , there exists such a set of items ${\mathcal {I}}$ with ${\displaystyle FFDH({\mathcal {I}})>\left(1+1/m-\varepsilon \right)$ $OPT({\mathcal {I$ ^[9]
만약 제가 모든 항목}}는 정사각형{\displaystyle{{나는\mathcal}, OPT(3/2)FFDH(나는)≤(나는)을 보유하고 있+h({\displaystyle FFDH({{나는}\mathcal})\leq(3/2)OPT({{나는}\mathcal})+h_{\max}}. 게다가, 각 ε>0{\displaystyle \varepsilon>0}, 존재하는 일련의 사각형 나 {\d $Isplaystyle {\mathcal {I$ $FFFDH({\mathcal {I}) 왼쪽(3/2-\varepsilon \right)$ 과 ${\mathcal {I}}$ 같이 $({\$ mathcal {I $FFDH({\mathcal {I}})>\left(3/2-\varepsilon \right)OPT({\mathcal {I}})$ 를 $표시$ 한다. $OPT({\mathcal {I$ ^[9]
생산되는 포장재는 단두대 포장이다.이는 항목들이 일련의 수평 또는 수직 가장자리 절단을 통해 얻을 수 있다는 것을 의미한다.

SF(Split-Fit 알고리즘)

이 알고리즘은 처음에 Coffman 등이 기술했다.^[9]항목 ${\mathcal {I}}$ ${\$ 과 ${\mathcal {I}}$ (와 $)$ 너비 $W$ {\ $displaystyle W}$ 인 스트립의 경우 다음과 같이 작동한다 $W$

$m\in \mathbb {N}$ $m\in \mathbb {N}$ N ${\$ 을(를) 결정하십시오 $m\in \mathbb {N}$ 이 정수 중 가장 큰 정수(예: 주어진 직사각형의 너비는 $W/m$ $W/m$ 이하임 $W/m$ ).
Divide ${\mathcal {I}}$ into two sets ${\mathcal {I}}_{wide}$ and ${\mathcal {I}}_{narrow}$ , such that ${\mathcal {I}}_{wide}$ contains all the items ${\displaystyle i\in {\mathcal {I$ $}}}$ with a width $w(i)>W/(m+1)$ while ${\mathcal {I}}_{narrow}$ contains all the items with $w(i)\leq W/(m+1)$ .
${\mathcal {I}}_{wide}$ ${\mathcal {I}}_{wide}$ i ${\mathcal {I}}_{wide}$ ${\mathcal {I}}_{wide}$ {\ $displaystyle$ {\ $mathcal {I}_{wide}}$ 을(를) 주문하고 ${\mathcal {I}}_{wide}$ ${\mathcal {I}}_{narrow}$ 는 ${\mathcal {I}}_{narrow}$ ${\mathcal {I}}_{narrow}$ w ${\$ {\ $mathcal{I}_{narrow}$ 을(를) 높이지 않은 높이로 ${\mathcal {I}}_{narrow}$ 주문한다.
${\mathcal {I}}_{wide}$ ${\mathcal {I}}_{wide}$ ${\mathcal {I}}_{wide}$ ${\mathcal {I}}_{wide}$ ${\$ 의 항목을 FFDH 알고리즘으로 포장하십시오 ${\mathcal {I}}_{wide}$ .
총 너비가 $W(m+1)/(m+2)$ + 1 $W(m+1)/(m+2)$ ) $W(m+1)/(m+2)$ / $W(m+1)/(m+2)$ ( $W(m+1)/(m+2)$ + 2 $W(m+1)/(m+2)$ ) $W(m+1)/(m+2)$ 보다 큰 모든 쉘프가 더 좁은 쉘프 아래에 오도록 $W(m+1)/(m+2)$ FFDH에 의해 구성된 레벨/쉘프를 다시 정렬하십시오.
이렇게 하면 의 $R$ 직사각형 영역 $R$ $R$ 이( $W/(m+2)$ W $W/(m+2)$ / ( $W/(m+2)$ + $W/(m+2)$ ) $W/(m+2)$ 과 $W/(m+2)$ 와) 함께 남으며, 이 항목은 포함되지 않는다.
${\mathcal {I}}_{narrow}$ $영역$ R $R$ 을 $R$ (를 $)$ 사용하여 ${\mathcal {I}}_{narrow}$ ${\mathcal {I}}_{narrow}$ a r ${\mathcal {I}}_{narrow}$ w {\displaystyle {\ $mathcal{I}_{narrow}$ 의 항목을 포장하려면 FFDH 알고리즘을 사용하십시오.

이 알고리즘에는 다음과 같은 속성이 있다.

나는}{\displaystyle{{나는\mathcal}항목의 모든 집합}와 해당하는 m{m\displaystyle}에게, SF(나는)≤(m+2)/OPT(나는)+(m+1)2h최대{\displaystyle SF({{나는}\mathcal})\leq(m+2)(m+1)OPT({{나는}\mathcal})+2h_{\max}}.[9]다는 것 m=1{\displaystyle m=1}, ho을 보유하고 있다.lds $SF({\mathcal {I}})\leq (3/2)OPT({\mathcal {I}})+2h_{\max }$ S $SF({\mathcal {I}})\leq (3/2)OPT({\mathcal {I}})+2h_{\max }$ ( $SF({\mathcal {I}})\leq (3/2)OPT({\mathcal {I}})+2h_{\max }$ ) $SF({\mathcal {I}})\leq (3/2)OPT({\mathcal {I}})+2h_{\max }$ ( $SF({\mathcal {I}})\leq (3/2)OPT({\mathcal {I}})+2h_{\max }$ / 2 $SF({\mathcal {I}})\leq (3/2)OPT({\mathcal {I}})+2h_{\max }$ ) O $SF({\mathcal {I}})\leq (3/2)OPT({\mathcal {I}})+2h_{\max }$ T $SF({\mathcal {I}})\leq (3/2)OPT({\mathcal {I}})+2h_{\max }$ ( $SF({\mathcal {I}})\leq (3/2)OPT({\mathcal {I}})+2h_{\max }$ ) $SF({\mathcal {I}})\leq (3/2)OPT({\mathcal {I}})+2h_{\max }$ + $SF({\mathcal {I}})\leq (3/2)OPT({\mathcal {I}})+2h_{\max }$ $SF({\mathcal {I}})\leq (3/2)OPT({\mathcal {I}})+2h_{\max }$ $SF({\mathcal {I}})\leq (3/2)OPT({\mathcal {I}})+2h_{\max }$ ${\$
For each $\varepsilon >0$ , there is a set of items ${\mathcal {I}}$ such that ${\displaystyle SF({\mathcal {I}})>\left((m+2)/(m+1)-\varepsilon \right)$ $OPT({\mathcal {I$ ^[9]

슬레이터 알고리즘

항목 ${\mathcal {I}}$ ${\$ 과 ${\mathcal {I}}$ (와 $)$ 너비 $W$ {\ $displaystyle W}$ 인 스트립의 경우 다음과 같이 작동한다 $W$

$W/2$ 이 W $W/2$ / $W/2$ ${\$ 디스플레이 $스타일 W/$ 2}보다 큰 모든 항목을 $W/2$ 찾아 스트립 하단에 (임의의 순서로) 쌓으십시오.이러한 항목의 총 높이를 h $h_{0}$ ${\$ 로 호출하십시오 $h_{0}$ 다른 모든 $h_{0}$ 은 $h_{0}$ 0 ${\$ 위에 배치됩니다 $h_{0}$
나머지 모든 항목을 높이를 증가하지 않는 순서로 정렬하십시오.그 품목들은 이 순서로 배치될 것이다.
$h_{0}$ 으로 h $h_{0}$ 0 {\ $displaystyle$ h_ ${0$ }의 수평선을 $h_{0}$ 고려한다.알고리즘은 어떤 아이템도 남기지 않거나 다음 아이템이 맞지 않을 때까지 이 선반 위의 아이템을 높이지 않는 순서로 배치한다.
스트립을 $W/2$ 한 두 부분으로 나누는 $W/2$ / 2 $W/2$ 에 수직선을 그린다 $W/2$
$h_{l}$ ${\$ 을(를) 왼쪽 절반의 어떤 항목으로 덮는 가장 높은 지점으로 하고 $h_{l}$ 오른쪽 절반의 해당 $h_{r}$ 지점인 $h_{r}$ $h_{r}$ ${\$ 스트립의 왼쪽과 오른쪽 반에 $h_{r}$ $h_{l}$ $h_{l}$ $W/2$ / $W/2$ ${\$ 및 $h_{r}$ r ${\$ 에 길이 $W/2$ $W/2$ / 2 $W/2$ 의 수평선 세그먼트를 그린다.이 두 선은 알고리즘이 3단계에서와 같이 항목을 배치할 새로운 선반을 구축한다.하단 선반이 있는 반쪽을 선택하고 다른 품목이 맞지 않을 때까지 이 선반 위에 물건을 놓으십시오.항목이 남아 있지 않을 때까지 이 단계를 반복하십시오.

이 알고리즘에는 다음과 같은 속성이 있다.

실행 시간은 ${\mathcal {O}}(|{\mathcal {I}}|\log(|{\mathcal {I}}|))$ ${\mathcal {O}}(|{\mathcal {I}}|\log(|{\mathcal {I}}|))$ ${\mathcal {O}}(|{\mathcal {I}}|\log(|{\mathcal {I}}|))$ ( I $){\displaystyle {\mathcal {O}({\mathcal {I})}({\mathcal {I})$ 로 한정할 수 있으며, ${\mathcal {O}}(|{\mathcal {I}}|)$ 이 ${\mathcal {O}}(|{\mathcal {I}}|\log(|{\mathcal {I}}|))$ O $I$ 로 이미 정렬된 경우 ${\mathcal {O}}(|{\mathcal {I}}|)$
For every set of items ${\mathcal {I}}$ it produces a packing of height ${\displaystyle A({\mathcal {I}})\leq 2OPT({\mathcal {I}})+h_{\max }/2\leq 2.5$ $OPT({\mathcal{I$ 여기서 $h_{\max }$ $h_{\max }$ ${\$ 는 $h_{\max }$ ${\mathcal {I}}$ ${\$ 에서 항목의 가장 ${\mathcal {I}}$ ^[10]큰 높이 입니다.

분할 알고리즘(SP)

이 알고리즘은 슬레이터의 접근법을 확장한 것으로 골란이 처음 기술한 것이다.^[11]그것은 폭이 증가하지 않는 순서로 항목을 배치한다.직관적인 아이디어는 스트립을 일부 항목을 배치하면서 하위 스트라이프로 분할하는 것이다.알고리즘은 가능할 때마다 이미 배치된 $항목$ j ${\$ $displaystyle$ j $}$ 의 현재 항목 i {\ $displaystyle$ $i}$ 을(를) 나란히 $i$ 배치한다 $j$ 이 경우 해당 하위 스트립은 첫 번째 항목 $j$ $j$ 을 $j$ (를) 포함하는 항목과 현재 항목 $i$ ${\displaystystyle$ i $}$ 을(를)로 분할한다.. 이 작업이 불가능한 경우 이미 배치된 항목 위에 $i$ $i$ ${\displaystyle$ i $}$ 을(를) 배치하고 하위 스트립을 분할하지 않는다.

이 알고리즘은 일련의 하위 스트라이프를 만든다.각 서브스트립에 대하여 우리는 그것의 왼쪽 하단 모서리와 , 그것의 너비, 그리고 그것의 너비뿐만 아니라 이 서브스트립 안에 가장 늦게 배치된 항목의 위쪽과 아래쪽 테두리에 평행한 수평선을 안다.

함수 분할 알고리즘(SP) 입력: 항목 I, 스트립 출력의 폭:A packing of the items     Sort I in nonincreasing order of widths;     Define empty list S of sub-strips;     Define a new sub-strip s with s.xposition = 0, s.yposition = 0, s.width = W, s.lower = 0, s.upper = 0, s.itemWidth = W;     Add s to S;     while I not empty do         i := I.pop(); Removes widest item from I         Define new list S_2s.width - s.itemWidth ≥ i.width; S_2는 S_2가 비어 있는 경우 이미 배치된 항목 옆에 맞는 모든 하위 스트립을 포함한다. 이 경우 항목을 다른 항목 위에 놓는다.가장 작은 s.upper를 가진 S에서 하위 스트립을 찾는다. 즉, 가장 적게 채워진 하위 스트립 i 위치(s.xposition, s.upper); 업데이트 s: s.lower := s.upper :=s.upper+i.높이; s.itemWidth := i.width; 이 경우 같은 수준의 다른 항목 옆에 항목을 놓고 이 위치에서 해당 하위 스트립을 분할한다.가장 작은 s.lower로 s ∈ S_2를 찾는다; i를 위치(s.xposition + s.itemWidth, s.lower);Remove s from S;             Define two new sub-strips s1 and s2 with              s1.xposition = s.xposition, s1.yposition = s.upper, s1.width = s.itemWidth, s1.lower = s.upper, s1.upper = s.upper, s1.itemWidth = s.itemWidth;             s2.xposition = s.xposition+s.itemWidth, s2.yposition = s.lower, s2.width = s.width - s.itemWidth,s2.lower = s.lower, s2.upper = i.height, s2.itemWidth = i.width; S.add(s1,s2); return end 함수

이 알고리즘에는 다음과 같은 속성이 있다.

하위 ${\mathcal {O}}(|{\mathcal {I}}|^{2})$ 트립의 수는 $|{\mathcal {I}}|$ $displaystyle$ ${\displaystyle {\mathcal {I} ^{2}({\$ $mathcal$ { $I}})$ 로 제한되므로 실행 시간은 O ${\mathcal {O}}(|{\mathcal {I}}|^{2})$ 2)로 ${\mathcal {O}}(|{\mathcal {I}}|^{2})$ 제한될 수 있다 $|{\mathcal {I}}|$
For any set of items ${\mathcal {I}}$ it holds that $SP({\mathcal {I}})\leq 2OPT({\mathcal {I}})+h_{\max }\leq 3OPT({\mathcal {I}})$ .^[11]
For any $\varepsilon >0$ , there exists a set of items ${\mathcal {I}}$ such that $SP({\mathcal {I}})>(3-\varepsilon )OPT({\mathcal {I}})$ .^[11]
For any $\varepsilon >0$ and $C>0$ , there exists a set of items ${\mathcal {I}}$ such that $SP({\mathcal {I}})>(2-\varepsilon )OPT({\mathcal {I}})+C$ .^[11]

리버스핏(RF)

이 알고리즘은 슈어마이어에 의해 처음 설명되었다.^[13]이 알고리즘에 대한 설명은 약간의 추가 표기법이 필요하다.배치 항목 $i\in {\mathcal {I}}$ $i\in {\mathcal {I}}$ $i\in {\mathcal {I}}$ ${\$ 의 경우 $i\in {\mathcal {I}}$ 왼쪽 하단 모서리는 $(a_{i},c_{i})$ $(a_{i},c_{i})$ ) ${\displaystyle(a_{i},c_{i}}})$ 으로 $(a_{i},c_{i})$ 표시되고 오른쪽 상단 $(b_{i},d_{i})$ 는 ( $b$ d i $(b_{i},d_{i})$ d $(b_{i},d_{i})$ ) ${\d,d_{i}}}}}$ 로 표시된다 $(b_{i},d_{i})$

항목 ${\mathcal {I}}$ ${\$ 과 ${\mathcal {I}}$ (와) 너비 $W$ $W$ 의 스트립을 지정하면 다음과 같이 작동한다 $W$

$W/2$ / $W/2$ $W/2$ 보다 큰 폭의 모든 직사각형을 스트립 하단에 서로 위로(임의의 순서로 $W/2$ ) 쌓으십시오. $H_{0}$ 스택의 높이를 $H_{0}$ $H_{0}$ 0 ${\$ 로 표시하십시오.다른 모든 품목은 H $H_{0}$ ${\$ 위에 포장된다 $H_{0}$
나머지 항목을 높이를 높이지 않는 순서대로 정렬하고 다음 단계에서 이 순서대로 고려하십시오. $h_{\max }$ $h_{\max }$ ${\$ 을(를) 이러한 나머지 항목 중 가장 높은 높이로 한다 $h_{\max }$ .
H $H_{0}$ ${\$ 에 의해 정의된 선반 위에 다른 품목이 맞지 않거나 남은 품목이 없을 때까지 $H_{0}$ 하나씩 왼쪽으로 정렬하여 놓으십시오.이 선반을 일급이라고 불러라.
$h_{1}$ ${\$ }를 언팩된 가장 높은 아이템의 높이가 되도록 $h_{1}$ 한다. $H_{0}+h_{\max }+h_{1}$ $H_{0}+h_{\max }+h_{1}$ 를 $H_{0}+h_{\max }+h_{1}$ 0 + $H_{0}+h_{\max }+h_{1}$ h $H_{0}+h_{\max }+h_{1}$ + $H_{0}+h_{\max }+h_{1}$ $H_{0}+h_{\max }+h_{1}$ {\ $displaystyle$ H_ ${0}+h_{\max }+h_{1$ }에 정의하십시오 $H_{0}+h_{\max }+h_{1}$ 알고리즘은 이 선반을 오른쪽에서 왼쪽으로 채우며, 선반에 물건이 닿도록 오른쪽으로 정렬한다.이 선반을 두 번째 역레벨이라고 불러라.
퍼스트핏(First-Fit)으로 인해 두 개의 선반(즉, 두 번째 선반)에 물건을 놓고, 다른 선반에 물건을 넣는다.남은 항목이 없거나 두 번째 선반에서 항목의 총 너비가 적어도 W $W/2$ / $W/2$ ${\displaystyle W/$ 2}이 $($ ) 될 때까지 계속 진행하십시오 $W/2$
두 번째 역레벨은 그 역레벨에서 한 항목이 1레벨에서 한 항목에 닿을 때까지 아래로 이동시킨다. $H_{1}$ ${\$ }를 시프트된 선반의 새로운 수직 위치로 정의하십시오 $H_{1}$ . $f$ $f$ 과 $f$ $s$ ${\$ $displaystyle s$ $}$ 을(를) 첫 번째 레벨에 배치하고 $f$ 두 번째 역레벨에 $s$ $s$ $s$ 을(를) 배치한 가장 적합한 항목 쌍으로 $s$ 두십시오. $x_{r}:=\max(b_{f},b_{s})$ $x_{r}:=\max(b_{f},b_{s})$ $x_{r}:=\max(b_{f},b_{s})$ $x_{r}:=\max(b_{f},b_{s})$ ( $x_{r}:=\max(b_{f},b_{s})$ f $x_{r}:=\max(b_{f},b_{s})$ , $x_{r}:=\max(b_{f},b_{s})$ $x_{r}:=\max(b_{f},b_{s})$ ) $x_{r}=\max(b_{f},b_{s}}$ 을(를) 정의하십시오 $x_{r}:=\max(b_{f},b_{s})$
$x_{r}<W/2$ $x_{r}<W/2$ < $x_{r}<W/2$ / 2 ${\displaystyle x_{r}<W/2})$ 인 $x_{r}<W/2$ 경우 $s$ $s$ 는 두 번째 역방향 레벨에 배치된 마지막 직사각형이다 $s$ .이 레벨에서 다른 모든 항목을 1단계에서 한 항목에 닿을 때까지(모든 동일한 양) 더 아래로 이동하십시오.다시 알고리즘은 $f$ $'$ ${\$ f $'}$ 과 $f'$ $s$ $'$ ${\$ 의 가장 오른쪽 쌍을 결정한다 $s'$ 선반이 아래로 이동된 양으로 $h_{2}$ $h_{2}$ $h_{2}$ ${\$ }}를 정의한다.
1. $h_{2}\leq h(s)$ $h_{2}\leq h(s)$ $h_{2}\leq h(s)$ $h_{2}\leq h(s)$ ( $h_{2}\leq h(s)$ ) $h_{2}\leq h(s)$ 인 경우 $s$ $s$ 이(가) 다른 항목이나 스트립의 테두리에 닿을 때까지 왼쪽으로 $s$ 이동하십시오 $h_{2}\leq h(s)$ . $s$ $'$ ${\$ 의 맨 위에 세 번째 수준을 정의하십시오 $s'$
2. $h_{2}>h(s)$ $h_{2}>h(s)$ > $h_{2}>h(s)$ ( ) ${\displaystyle h_$ {2 $}>h}이($ 가 $h_{2}>h(s)$ $)$ {\ $displaystyle$ s $}$ 인 경우, shift $s$ ${\$ $displaystyle s}$ 은(는 $)$ $s$ $'$ ${\$ s $'}$ 의 맨 위에 세 번째 레벨을 정의하고 $s$ $s'$ 왼쪽의 첫 번째 레벨에서 한 항목에 닿도록 $s$ 를 배치한다 $s$ .
First-Fit 휴리스틱을 사용하여 아이템을 계속 포장하십시오.다음의 각 레벨(레벨 3에서 시작)은 이전 레벨에서 가장 큰 항목의 상단을 통과하는 수평선에 의해 정의된다.다음 레벨에 배치된 첫 번째 항목은 왼쪽 측면으로 스트립의 테두리를 건드리지 않고 첫 번째 레벨의 항목 $또는$ $s$ 항목에 닿을 수 있다는 점에 유의하십시오 $s$

이 알고리즘에는 다음과 같은 속성이 있다.

실행 시간은 최대 $|{\mathcal {I}}|$ $displaystyle$ ${\mathcal {O$ $}({\mathcal$ ${I$ $}^{2$ $})$ 레벨이 있으므로 $|{\mathcal {I}}|$ ${\mathcal {O}}(|{\mathcal {I}}|^{2})$ 2)로 제한될 수 있다.
항목 ${\mathcal {I}}$ ${\$ 의 모든 세트에 대해 높이 ${\mathcal {I}}$ $RF({\mathcal {I}})\leq 2OPT({\mathcal {I}})$ ( $RF({\mathcal {I}})\leq 2OPT({\mathcal {I}})$ ) $RF({\mathcal {I}})\leq 2OPT({\mathcal {I}})$ 2 $RF({\mathcal {I}})\leq 2OPT({\mathcal {I}})$ $RF({\mathcal {I}})\leq 2OPT({\mathcal {I}})$ T $RF({\mathcal {I}})\leq 2OPT({\mathcal {I}})$ ( $RF({\mathcal {I}})\leq 2OPT({\mathcal {I}})$ ) $RF({\mathcal {I})\leq 2OPT({\mathcal {I})$ 의 패킹을 생성한다 $RF({\mathcal {I}})\leq 2OPT({\mathcal {I}})$ ^[13]

스타인버그 알고리즘(ST)

스타인버그 알고리즘은 재귀적인 알고리즘이다. $I$ ${\$ 과 ${\mathcal {I}}$ (와) 너비 W {\ $displaystyle W}$ 및 높이 $W$ $H$ {\ $displaystyle H}$ 의 직사각형 대상 영역 집합에 따라 4개의 감소 규칙을 제안하며 $H$ 이 규칙에서 일부 항목을 배치하고 나머지 부분과 관련하여 이전과 동일한 특성을 가진 더 작은 직사각형 영역을 남긴다.우랄 아이템Consider the following notations: Given a set of items ${\mathcal {I}}$ we denote by $h_{\max }({\mathcal {I}})$ the tallest item height in ${\mathcal {I}}$ , $w_{\max }({\mathcal {I}})$ the largest item width가 I ${\$ 및 ${\mathcal {I}}$ A $\mathrm {AREA} ({\mathcal {I}}):=\sum _{i\in {\mathcal {I}}}w(i)h(i)$ $\mathrm {AREA} ({\mathcal {I}}):=\sum _{i\in {\mathcal {I}}}w(i)h(i)$ $\mathrm {AREA} ({\mathcal {I}}):=\sum _{i\in {\mathcal {I}}}w(i)h(i)$ ( $\mathrm {AREA} ({\mathcal {I}}):=\sum _{i\in {\mathcal {I}}}w(i)h(i)$ ) $\mathrm {AREA} ({\mathcal {I}}):=\sum _{i\in {\mathcal {I}}}w(i)h(i)$ $\mathrm {AREA} ({\mathcal {I}}):=\sum _{i\in {\mathcal {I}}}w(i)h(i)$ $\mathrm {AREA} ({\mathcal {I}}):=\sum _{i\in {\mathcal {I}}}w(i)h(i)$ ( $\mathrm {AREA} ({\mathcal {I}}):=\sum _{i\in {\mathcal {I}}}w(i)h(i)$ ) $\mathrm {AREA} ({\mathcal {I}}):=\sum _{i\in {\mathcal {I}}}w(i)h(i)$ ( $\mathrm {AREA} ({\mathcal {I}}):=\sum _{i\in {\mathcal {I}}}w(i)h(i)$ ) ${\displaystyle \mathrm {ARE}({\mathcal {I}):$ $=\sum _{i\in {\mathcal{I}}w(i)h(i)}}$ 이(가) 이들 항목의 총 면적 $\mathrm {AREA} ({\mathcal {I}}):=\sum _{i\in {\mathcal {I}}}w(i)h(i)$ .스타인버그는 만약

$h_{\max }({\mathcal {I}})\leq H$ , $w_{\max }({\mathcal {I}})\leq W$ , and ${\displaystyle \mathrm {AREA} ({\mathcal {I}})\leq W\cdot H-(2h_{\max }({\ma$ $thcal{I}}-{{w_{\max}({\mathcal{I}}}-W)_$ $(a)_{+}:=\max\{0,a\}$ 서 $(a)_{+}:=\max\{0,a\}$ ( ) $(a)_{+}:=\max\{0,a\}$ + : $(a)_{+}:=\max\{0,a\}$ = $(a)_{+}:=\max\{0,a\}$ { $(a)_{+}:=\max\{0,a\}$ ${\displaystyle (a)_{+}}=\max$ \{0 $,a$

그러면 모든 항목은 크기 $W\times H$ $W\times H$ $H의 목표$ 영역 안에 배치될 수 있다 $W\times H$ 각 $감소$ 규칙은 더 작은 목표 영역과 배치해야 하는 항목의 하위 집합을 산출할 것이다 $.$ 위의 조건이 절차를 시작하기 전에 유지되면 생성된 하위 문제도 이 속성을 가질 것이다.

절차 1: $w_{\max }({\mathcal {I}}')\geq W/2$ $w_{\max }({\mathcal {I}}')\geq W/2$ ( $w_{\max }({\mathcal {I}}')\geq W/2$ $w_{\max }({\mathcal {I}}')\geq W/2$ ) $w_{\max }({\mathcal {I}}')\geq W/2$ $w_{\max }({\mathcal {I}}')\geq W/2$ / $w_{\max }({\mathcal {I}}')\geq W/2$ $w_{\max }({\mathcal {I}})\geq W/2$ 인 경우 적용할 수 있다 $w_{\max }({\mathcal {I}}')\geq W/2$

$w(i)\geq W/2$ 가 w ( $w(i)\geq W/2$ )인 $i\in {\mathcal {I}}$ $w(i)\geq W/2$ I ${\displaystyle$ i\in {\ $mathcal$ { $I}}$ 을 $w(i)\geq W/2$ 를) $i\in {\mathcal {I}}$ W / 2 {\ $displaystyle$ $w(i)\geq W/2}$ 인 $i\in {\mathcal {I}}$ 모든 $i\in {\mathcal {I}}$ 을 찾아 $w(i)\geq W/2$ ${\mathcal {I}}$ ${\$ 에서 제거하십시오 ${\mathcal {I}}$
비증가 너비로 정렬하고 대상 영역의 맨 아래에 좌 정렬한다. $h_{0}$ $h_{0}$ ${\$ 을(를) 총 높이로 한다 $h_{0}$ .
$i\in {\mathcal {I}}$ $h(i)>H-h_{0}$ ) $h(i)>H-h_{0}$ > $h(i)>H-h_{0}$ - $h(i)>H-h_{0}$ 0 ${\$ displaystyle $h$ $(i$ $)}$ 의 모든 $h(i)>H-h_{0}$ { I {\displaystyle i $\$ $in$ ${\mathcal {I}}$ 을(를) $찾으십시오$ $.$ $H-h_{0$ ${\mathcal {I}}$ ${\$ 에서 제거한 후 새로운 ${\mathcal {I}}$ 세트 ${\mathcal {I}}_{H}$ ${\mathcal {I}}_{H}$ ${\$ 에 넣는다 ${\mathcal {I}}_{H}$
${\mathcal {I}}_{H}$ ${\$ $H}}$ 은 ${\mathcal {I}}_{H}$ (는) 비어 있으며, 새로운 대상 영역을 $h_{0}$ $h_{0}$ ${\$ 위의 영역으로 정의하십시오 $W$ 즉, $H-h_{0}$ H $H-h_{0}$ - $H-h_{0}$ $H-h_{0}$ ${\$ 과 $H-h_{0}$ $너비$ W ${\displaystystyle W}.$ 이 새로운 대상 영역과 축소된 항목 세트로 구성된 문제를 절차 중 하나로 해결하십시오.
${\mathcal {I}}_{H}$ ${\$ $H}}$ 은 ${\mathcal {I}}_{H}$ (는) 비어 있지 않은 상태에서 높이를 높이지 않게 정렬하고 대상 영역의 오른쪽 상단 모서리에 하나씩 정확하게 맞춘 아이템을 배치한다. $w_{0}$ $w_{0}$ ${\$ 을 이 항목의 $w_{0}$ 총 너비로 한다.왼쪽 상단 모서리에 $W-w_{0}$ $H-h_{0}$ W $W-w_{0}$ - $W-w_{0}$ $W-w_{0}$ ${\$ 과 $W-w_{0}$ $H-h_{0}$ H - $H-h_{0}$ 0 $H-h_{0}$ {\ $displaystyle H-h_{0}$ 이 있는 새 대상 영역을 정의하십시오.이 새로운 대상 영역과 축소된 항목 집합으로 구성된 문제를 절차 중 하나로 해결하십시오.

Procedure 2: It can be applied if the following conditions hold: $w_{\max }({\mathcal {I}})\leq W/2$ , $h_{\max }({\mathcal {I}})\leq H/2$ , and there exist two different items $i,i'\in {\mathcal {I}}$ with $w(i)\geq W/4$ $w(i)\geq W/4$ , $w(i')\geq W/4$ , $h(i)\geq H/4$ , $h(i')\geq H/4$ and $2(\mathrm {AREA} ({\mathcal {I}})-w(i)h(i)-w(i')h(i'))\leq (W-\max\{w(i),w(i')\})H$ ${\displaystyle 2(\mathrm {I})({\mathcal$ $H}$ $2(\mathrm {AREA} ({\mathcal {I}})-w(i)h(i)-w(i')h(i'))\leq (W-\max\{w(i),w(i')\})H$

$i$ $i$ 및 $i$ $i$ $'$ ${\$ 을(를) 찾아서 $i'$ ${\mathcal {I}}$ ${\$ 에서 제거하십시오 ${\mathcal {I}}$
대상 영역의 왼쪽 하단 모서리에 더 넓은 것을 배치하고 왼쪽 정렬이 더 좁은 것을 첫 번째 영역의 맨 위에 배치한다.
$W-\max\{w(i),w(i')\}$ 두 항목의 오른쪽에 W $W-\max\{w(i),w(i')\}$ - $W-\max\{w(i),w(i')\}$ { $W-\max\{w(i),w(i')\}$ ( i $W-\max\{w(i),w(i')\}$ ) $W-\max\{w(i),w(i')\}$ , w ( $W-\max\{w(i),w(i')\}$ ) $W-\max\{w(i),w(i')\}$ $W-\max\{w(i),w(i')\$ 및 $H$ H $H$ 을(를) 가질 수 있도록 새 대상 영역을 정의하십시오 $H$
절차 중 하나를 사용하여 ${\mathcal {I}}$ ${\$ 에 있는 잔여 항목을 새 대상 영역에 ${\mathcal {I}}$ 배치하십시오.

절차 3:경우 다음과 같은 조건이 유지된다면 그것은 적용할 수 있습니다. w정도이다(나는)≤ W/2{\displaystyle w_{\max}({{나는}\mathcal})\leq W/2}, h max(나는)≤ H/2{\displaystyle h_{\max}({{나는}\mathcal})\leq H/2}, 나는입니다., 1{\displaystyle{{나는\mathcal}}>1}, decreasin까지 해당 품목을 구분.gwidth there exist an index $m$ such that when defining ${\mathcal {I'}}$ as the first $m$ items it holds that ${\displaystyle \mathrm {AREA} ({\mathcal {I}})-WH/4\leq \mathrm {AREA} ({\mathcal {I'$ $}})\leq 3WH/8}$ 및 $\mathrm {AREA} ({\mathcal {I}})-WH/4\leq \mathrm {AREA} ({\mathcal {I'}})\leq 3WH/8$ $w(i_{m+1})\leq W/4$ ( $w(i_{m+1})\leq W/4$ m $w(i_{m+1})\leq W/4$ + 1 $w(i_{m+1})\leq W/4$ ) $w(i_{m+1})\leq W/4$ W $w(i_{m+1})\leq W/4$ / $w(i_{m+1})\leq W/4$ $w(i_{m+1})\leq W/4$

$W_{1}:=\max {W/2,2\mathrm {AREA} ({\mathcal {I'}})/H}$ $W_{1}:=\max {W/2,2\mathrm {AREA} ({\mathcal {I'}})/H}$ $W_{1}:=\max {W/2,2\mathrm {AREA} ({\mathcal {I'}})/H}$ $W_{1}:=\max {W/2,2\mathrm {AREA} ({\mathcal {I'}})/H}$ $W_{1}:=\max {W/2,2\mathrm {AREA} ({\mathcal {I'}})/H}$ / $W_{1}:=\max {W/2,2\mathrm {AREA} ({\mathcal {I'}})/H}$ , $W_{1}:=\max {W/2,2\mathrm {AREA} ({\mathcal {I'}})/H}$ A $W_{1}:=\max {W/2,2\mathrm {AREA} ({\mathcal {I'}})/H}$ $W_{1}:=\max {W/2,2\mathrm {AREA} ({\mathcal {I'}})/H}$ $W_{1}:=\max {W/2,2\mathrm {AREA} ({\mathcal {I'}})/H}$ ( $W_{1}:=\max {W/2,2\mathrm {AREA} ({\mathcal {I'}})/H}$ $W_{1}:=\max {W/2,2\mathrm {AREA} ({\mathcal {I'}})/H}$ ) $W_{1}:=\max {W/2,2\mathrm {AREA} ({\mathcal {I'}})/H}$ / $W_{1}:=\max {W/2,2\mathrm {AREA} ({\mathcal {I'}})/H}$ ${\$ 를 설정하십시오 $W_{1}:=\max {W/2,2\mathrm {AREA} ({\mathcal {I'}})/H}$
높이 $H$ $H$ 및 $H$ 너비 $W_{1}$ $W_{1}$ ${\$ }인 원래 대상의 왼쪽 하단 모서리에 한 개의 새로운 직사각형 대상 영역을 정의하고 $W_{1}$ , 나머지 한 개의 영역은 $높이$ H $H$ 및 $H$ $W-W_{1}$ W - $W-W_{1}$ 1 $W-W_{1}$ {\ $displaystyle W-W_{1$
절차 중 하나를 사용하여 $′{\$ 에 있는 항목을 첫 번째 새 대상 영역에 배치하고 ${\mathcal {I'}}$ ${\mathcal {I}}\setminus {\mathcal {I'}}$ ${\mathcal {I}}\setminus {\mathcal {I'}}$ $′{\displaystyle {I}\setminus {\mathcal}$ 에 있는 항목을 두 번째 영역에 ${\mathcal {I}}\setminus {\mathcal {I'}}$ 배치하십시오.

절차 1 ~ 3은 항목 및 대상 영역의 높이와 너비를 교환할 때 대칭 버전을 갖는다는 점에 유의하십시오.

Procedure 4: It can be applied if the following conditions hold: $w_{\max }({\mathcal {I}})\leq W/2$ , $h_{\max }({\mathcal {I}})\leq H/2$ , and there exists an item $i\in {\mathcal {I}}$ such that $w(i)h(i)\geq \mathrm {AREA} ({\mathcal {I}})-WH/4$ $w(i)h(i)\geq \mathrm {AREA} ({\mathcal {I}})-WH/4$ A $w(i)h(i)\geq \mathrm {AREA} ({\mathcal {I}})-WH/4$ E $w(i)h(i)\geq \mathrm {AREA} ({\mathcal {I}})-WH/4$ ( $w(i)h(i)\geq \mathrm {AREA} ({\mathcal {I}})-WH/4$ ) $w(i)h(i)\geq \mathrm {AREA} ({\mathcal {I}})-WH/4$ - $w(i)h(i)\geq \mathrm {AREA} ({\mathcal {I}})-WH/4$ $w(i)h(i)\geq \mathrm {AREA} ({\mathcal {I}})-WH/4$ / 4 ${\displaystyle w(i)h(i)\geq \mathrm {ARIA}({\mathcal {I})-WH/4$

대상 영역의 왼쪽 하단 모서리에 항목 $i$ $i$ $i$ 을(를) 배치하고 ${\mathcal {I}}$ ${\$ 에서 제거하십시오 ${\mathcal {I}}$
$W-w(i)$ W $W-w(i)$ - $W-w(i)$ ( $W-w(i)$ ) $W-w(i)$ 및 $W-w(i)$ $높이$ H $H$ 을(를) 갖도록 이 항목의 새 대상 영역 오른쪽을 정의하고 $H$ 절차 중 하나를 사용하여 이 영역 내에 나머지 항목을 배치하십시오.

이 알고리즘에는 다음과 같은 속성이 있다.

실행 시간은 ${\mathcal {O}}(|{\mathcal {I}}|\log(|{\mathcal {I}}|)^{2}/\log(\log(|{\mathcal {I}}|)))$ ${\mathcal {O}}(|{\mathcal {I}}|\log(|{\mathcal {I}}|)^{2}/\log(\log(|{\mathcal {I}}|)))$ ${\mathcal {O}}(|{\mathcal {I}}|\log(|{\mathcal {I}}|)^{2}/\log(\log(|{\mathcal {I}}|)))$ ( ${\mathcal {O}}(|{\mathcal {I}}|\log(|{\mathcal {I}}|)^{2}/\log(\log(|{\mathcal {I}}|)))$ ) 2 ${\mathcal {O}}(|{\mathcal {I}}|\log(|{\mathcal {I}}|)^{2}/\log(\log(|{\mathcal {I}}|)))$ / ${\mathcal {O}}(|{\mathcal {I}}|\log(|{\mathcal {I}}|)^{2}/\log(\log(|{\mathcal {I}}|)))$ ${\mathcal {O}}(|{\mathcal {I}}|\log(|{\mathcal {I}}|)^{2}/\log(\log(|{\mathcal {I}}|)))$ ( ${\mathcal {O}}(|{\mathcal {I}}|\log(|{\mathcal {I}}|)^{2}/\log(\log(|{\mathcal {I}}|)))$ I ${\mathcal {O}}(|{\mathcal {I}}|\log(|{\mathcal {I}}|)^{2}/\log(\log(|{\mathcal {I}}|)))$ ) $){\displaystyle {\mathcal {O}({\mathcal {I}) \log({\mathcal {I$ }}){ $2}/\log(\log({\mathcal {I}$ ${\mathcal {O}}(|{\mathcal {I}}|\log(|{\mathcal {I}}|)^{2}/\log(\log(|{\mathcal {I}}|)))$ ^[8]로 제한될 수 있다.
항목 ${\mathcal {I}}$ ${\$ $ST({\mathcal {I}})\leq 2OPT({\mathcal {I}})$ $}$ 의 모든 세트에 대해 높이 ${\mathcal {I}}$ S $ST({\mathcal {I}})\leq 2OPT({\mathcal {I}})$ ( I $ST({\mathcal {I}})\leq 2OPT({\mathcal {I}})$ ) $ST({\mathcal {I}})\leq 2OPT({\mathcal {I}})$ $ST({\mathcal {I}})\leq 2OPT({\mathcal {I}})$ $ST({\mathcal {I}})\leq 2OPT({\mathcal {I}})$ P $ST({\mathcal {I}})\leq 2OPT({\mathcal {I}})$ ( $ST({\mathcal {I}})\leq 2OPT({\mathcal {I}})$ ) $ST({\mathcal {I})\leq 2OPT({\mathcal {I})$ 의 패킹을 생성한다 $ST({\mathcal {I}})\leq 2OPT({\mathcal {I}})$ ^[8]

의사-폴리놈 시간 근사 알고리즘

다항식 시간 $3/2$ 에 $3/2$ 대한 하한 $3/2$ / 2 $[\displaystyle 3/2$ }을 $($ 를) 개선하기 위해 스트립 패킹 문제에 대한 유사 다항식 시간 알고리즘이 고려되었다.이러한 유형의 알고리즘을 고려할 때, 항목과 스트립의 모든 크기가 통합으로 주어진다.또한 스트립 $W$ $W$ 의 너비는 실행 시간에 다항식으로 나타날 수 있다 $W$ .주어진 경우 스트립의 너비는 $\log(W)$ $\log(W)$ ( $\log(W)$ ) $\log(W)$ 의 인코딩 크기를 필요로 하기 때문에 이 시간은 더 이상 다항식 실행 시간으로 간주되지 않는다는 점에 유의하십시오 $\log(W)$

개발된 사이비-폴리놈 시간 알고리즘은 대부분 같은 접근법을 사용한다.각 최적 용액을 단순화하여 일정한 수의 구조 중 하나를 가진 용액으로 변환할 수 있음을 알 수 있다.그런 다음 알고리즘은 이 모든 구조를 반복하고 선형 및 동적 프로그래밍을 사용하여 항목을 내부에 배치한다.지금까지 달성한 최상의 비율은 $(5/4+\varepsilon )OPT(I)$ ( $(5/4+\varepsilon )OPT(I)$ / $(5/4+\varepsilon )OPT(I)$ + $(5/4+\varepsilon )OPT(I)$ ) $(5/4+\varepsilon )OPT(I)$ $(5/4+\varepsilon )OPT(I)$ $(5/4+\varepsilon )OPT(I)$ ( I $(5/4+\varepsilon )OPT(I)$ ) $(5/4+\varempsilon )OPT(I)$ 이며 $(5/4+\varepsilon )OPT(I)$ ^[19] $P=NP$ = $P=NP$ $P=NP$ $P=NP$ 이 아닌 $5/4$ 한 $5/4$ / $5/4$ $5/4$ 보다 나은 비율을 가진 유사-pymonalm 알고리즘은 있을 수 없다.

의사-다항식 시간 근사치 개요
연도	근사 비율	출처	댓글
2010	${\displaystyle(3/2+\varepsilon )}$	얀센, 툴레^[20]
2016	${\displaystyle(7/5 이상\displaystyle(7/5 이상)$	나디라제, 비제^[21]
2016	$(4/3+\varepsilon )$	갈베즈^[22], 그란도니, 잉갈라, 칸	또한 90도 회전도.
2017	$(4/3+\varepsilon )$	얀센^[23] 주
2019	${\displaystyle(5/4+\barepsilon )}$	얀센^[19] 주	또한 90도 회전 및 연속적인 금형 작업용

온라인 알고리즘

스트립 패킹의 온라인 변종에서는 시간이 지남에 따라 물건이 도착한다.물건이 도착하면 바로 다음 물건이 알려지기 전에 갖다 놓아야 한다.고려된 온라인 알고리즘에는 두 가지 유형이 있다.첫 번째 변종에서는 일단 품목을 배치하면 패킹을 변경할 수 없다.두 번째 항목에서는 다른 항목이 도착하면 다시 포장할 수 있다.이 변종을 마이그레이션 모델이라고 한다.

온라인 알고리즘의 품질은 (절대) 경쟁률로 측정된다.

$\mathrm {sup} _{I}A(I)/OPT(I)$ $\mathrm {sup} _{I}A(I)/OPT(I)$ $\mathrm {sup} _{I}A(I)/OPT(I)$ $\mathrm {sup} _{I}A(I)/OPT(I)$ $\mathrm {sup} _{I}A(I)/OPT(I)$ ( I $\mathrm {sup} _{I}A(I)/OPT(I)$ ) $\mathrm {sup} _{I}A(I)/OPT(I)$ / $\mathrm {sup} _{I}A(I)/OPT(I)$ $\mathrm {sup} _{I}A(I)/OPT(I)$ T $\mathrm {sup} _{I}A(I)/OPT(I)$ ( $\mathrm {sup} _{I}A(I)/OPT(I)$ ) ${\displaystyle \mathrmat {sup} _{I}A(I)/OPT(I$

여기서 $A(I)$ ( $A(I)$ ) $A(I)$ 은 온라인 알고리즘에 의해 생성된 솔루션에 해당하고 $A(I)$ $OPT(I)$ P $OPT(I)$ ( $OPT(I)$ ) $OPT(I)$ 은 최적 솔루션의 $OPT(I)$ 크기에 해당한다.절대 경쟁률 외에도 온라인 알고리즘의 점증적 경쟁률이 연구되었다. $h_{\max }(I)\leq 1$ ( $h_{\max }(I)\leq 1$ )가 $h_{\max }(I)\leq 1$ 인스턴스 $I$ ${\$ $displaystyle h_{\max }(I)\leq 1$ 의 경우 다음과 $h_{\max }(I)\leq 1$ 같이 정의된다.

$\lim \mathrm {sup} _{OPT(I)\rightarrow \infty }A(I)/OPT(I)$ s $\lim \mathrm {sup} _{OPT(I)\rightarrow \infty }A(I)/OPT(I)$ $\lim \mathrm {sup} _{OPT(I)\rightarrow \infty }A(I)/OPT(I)$ $\lim \mathrm {sup} _{OPT(I)\rightarrow \infty }A(I)/OPT(I)$ O $\lim \mathrm {sup} _{OPT(I)\rightarrow \infty }A(I)/OPT(I)$ P $\lim \mathrm {sup} _{OPT(I)\rightarrow \infty }A(I)/OPT(I)$ ( $\lim \mathrm {sup} _{OPT(I)\rightarrow \infty }A(I)/OPT(I)$ ) → $\lim \mathrm {sup} _{OPT(I)\rightarrow \infty }A(I)/OPT(I)$ ( I ) $\lim \mathrm {sup} _{OPT(I)\rightarrow \infty }A(I)/OPT(I)$ / $\lim \mathrm {sup} _{OPT(I)\rightarrow \infty }A(I)/OPT(I)$ O P $\lim \mathrm {sup} _{OPT(I)\rightarrow \infty }A(I)/OPT(I)$ T $\lim \mathrm {sup} _{OPT(I)\rightarrow \infty }A(I)/OPT(I)$ ( $\lim \mathrm {sup} _{OPT(I)\rightarrow \infty }A(I)/OPT(I)$ ) {\ $displaystyle \mathrm {sup} _{OPT(I)\오른쪽$ 화살표 $\inft }A(I)/OPT(I$

$h_{\max }(I)\leq 1$ 인스턴스는 h $h_{\max }(I)\leq 1$ ( $h_{\max }(I)\leq 1$ ) $h_{\max }(I)\leq 1$ $h_{\max }(I)\leq 1$ $h_{\max }(I)\leq 1$ 처럼 확장할 수 있다는 점에 유의하십시오 $h_{\max }(I)\leq 1$

마이그레이션이 없는 온라인 알고리즘 개요
연도	경쟁률	점근 경쟁률	출처
1983	6.99	$(\디스플레이 스타일 \displaystyle \$	베이커와 슈바르츠^[24]
1997		$1.69+\varepsilon }$	시리크와 우잉거^[25]
2007	6.6623		후링크와 파울루스^[26]
2009	6.6623		예^[27], 한, 장
2007		$(\displaystyle 1.5889}$	한 외 +^[28] 세이덴^[29]

온라인 빈 패킹 알고리즘이 슈퍼하모니틱 등급에 속할 경우 온라인 설정에 Han ^[28]등 프레임워크가 적용된다.따라서 세이덴의 온라인 빈 패킹 알고리즘 하모니크++^[29]는 점증비 1.5889의 온라인 스트립 패킹 알고리즘을 내포하고 있다.

마이그레이션 없는 온라인 알고리즘에 대한 하한 개요
연도	경쟁률	점근 경쟁률	출처	댓글
1982	$2$		브라운, 베이커, 캣세프^[30]
2006	2.25		요하네스^[31]	또한 병렬 작업 스케줄링 문제를 해결한다.
2007	2.43		후링크와 파울루스^[32]	또한 병렬 작업 스케줄링 문제를 해결한다.
2009	2.457		케른과 파울루스
2012		$(\displaystyle 1.5404}$	발로흐 베케시^[34]	기본 빈 패킹 문제로 인한 하한
2016	2.618		유, 마오, 샤오^[35]

참조

^ Wäscher, Gerhard; Haußner, Heike; Schumann, Holger (16 December 2007). "An improved typology of cutting and packing problems". European Journal of Operational Research. 183 (3): 1109–1130. doi:10.1016/j.ejor.2005.12.047. ISSN 0377-2217.
^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j Baker, Brenda S.; Coffman Jr., Edward G.; Rivest, Ronald L. (1980). "Orthogonal Packings in Two Dimensions". SIAM J. Comput. 9 (4): 846–855. doi:10.1137/0209064.
^ ^a ^b Harren, Rolf; Jansen, Klaus; Prädel, Lars; van Stee, Rob (February 2014). "A (5/3 + epsilon)-approximation for strip packing". Computational Geometry. 47 (2): 248–267. doi:10.1016/j.comgeo.2013.08.008.
^ Neuenfeldt Junior, Alvaro Luiz. "The Two-Dimensional Rectangular Strip Packing Problem" (PDF). 10820228.
^ ^a ^b Henning, Sören; Jansen, Klaus; Rau, Malin; Schmarje, Lars (2019). "Complexity and Inapproximability Results for Parallel Task Scheduling and Strip Packing". Theory of Computing Systems. 64: 120–140. arXiv:1705.04587. doi:10.1007/s00224-019-09910-6. S2CID 67168004.
^ Ashok, Pradeesha; Kolay, Sudeshna; Meesum, S.M.; Saurabh, Saket (January 2017). "Parameterized complexity of Strip Packing and Minimum Volume Packing". Theoretical Computer Science. 661: 56–64. doi:10.1016/j.tcs.2016.11.034.
^ ^a ^b ^c Martello, Silvano; Monaci, Michele; Vigo, Daniele (1 August 2003). "An Exact Approach to the Strip-Packing Problem". INFORMS Journal on Computing. 15 (3): 310–319. doi:10.1287/ijoc.15.3.310.16082. ISSN 1091-9856.
^ ^a ^b ^c ^d Steinberg, A. (March 1997). "A Strip-Packing Algorithm with Absolute Performance Bound 2". SIAM Journal on Computing. 26 (2): 401–409. doi:10.1137/S0097539793255801.
^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ^k Coffman Jr., Edward G.; Garey, M. R.; Johnson, David S.; Tarjan, Robert Endre (1980). "Performance Bounds for Level-Oriented Two-Dimensional Packing Algorithms". SIAM J. Comput. 9 (4): 808–826. doi:10.1137/0209062.
^ ^a ^b Sleator, Daniel Dominic (1980). "A 2.5 Times Optimal Algorithm for Packing in Two Dimensions". Inf. Process. Lett. 10: 37–40. doi:10.1016/0020-0190(80)90121-0.
^ ^a ^b ^c ^d ^e Golan, Igal (August 1981). "Performance Bounds for Orthogonal Oriented Two-Dimensional Packing Algorithms". SIAM Journal on Computing. 10 (3): 571–582. doi:10.1137/0210042.
^ Baker, Brenda S; Brown, Donna J; Katseff, Howard P (December 1981). "A 5/4 algorithm for two-dimensional packing". Journal of Algorithms. 2 (4): 348–368. doi:10.1016/0196-6774(81)90034-1.
^ ^a ^b ^c Schiermeyer, Ingo (1994). "Reverse-Fit: A 2-optimal algorithm for packing rectangles". Algorithms — ESA '94. Lecture Notes in Computer Science. Vol. 855. Springer Berlin Heidelberg. pp. 290–299. doi:10.1007/bfb0049416. ISBN 978-3-540-58434-6.
^ Kenyon, Claire; Rémila, Eric (November 2000). "A Near-Optimal Solution to a Two-Dimensional Cutting Stock Problem". Mathematics of Operations Research. 25 (4): 645–656. doi:10.1287/moor.25.4.645.12118. S2CID 5361969.
^ Harren, Rolf; van Stee, Rob (2009). "Improved Absolute Approximation Ratios for Two-Dimensional Packing Problems". Approximation, Randomization, and Combinatorial Optimization. Algorithms and Techniques, 12th International Workshop, {APPROX} 2009, and 13th International Workshop, {RANDOM} 2009, Berkeley, CA, USA, August 21–23, 2009. Proceedings. 5687: 177–189. Bibcode:2009LNCS.5687..177H. doi:10.1007/978-3-642-03685-9_14.
^ Jansen, Klaus; Solis-Oba, Roberto (August 2009). "Rectangle packing with one-dimensional resource augmentation". Discrete Optimization. 6 (3): 310–323. doi:10.1016/j.disopt.2009.04.001.
^ Bougeret, Marin; Dutot, Pierre-Francois; Jansen, Klaus; Robenek, Christina; Trystram, Denis (5 April 2012). "Approximation Algorithms for Multiple Strip Packing and Scheduking Parallel Jobs in Platforms". Discrete Mathematics, Algorithms and Applications. 03 (4): 553–586. doi:10.1142/S1793830911001413.
^ Sviridenko, Maxim (January 2012). "A note on the Kenyon–Remila strip-packing algorithm". Information Processing Letters. 112 (1–2): 10–12. doi:10.1016/j.ipl.2011.10.003.
^ ^a ^b Jansen, Klaus; Rau, Malin (2019). "Closing the Gap for Pseudo-Polynomial Strip Packing". 27th Annual European Symposium on Algorithms (ESA 2019). Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik. 144: 62:1–62:14. doi:10.4230/LIPIcs.ESA.2019.62. S2CID 24303167.
^ Jansen, Klaus; Thöle, Ralf (January 2010). "Approximation Algorithms for Scheduling Parallel Jobs". SIAM Journal on Computing. 39 (8): 3571–3615. doi:10.1137/080736491.
^ Nadiradze, Giorgi; Wiese, Andreas (21 December 2015). "On approximating strip packing with a better ratio than 3/2". Proceedings of the Twenty-Seventh Annual ACM-SIAM Symposium on Discrete Algorithms. Society for Industrial and Applied Mathematics: 1491–1510. doi:10.1137/1.9781611974331.ch102. ISBN 978-1-61197-433-1.
^ Gálvez, Waldo; Grandoni, Fabrizio; Ingala, Salvatore; Khan, Arindam (2016). "Improved Pseudo-Polynomial-Time Approximation for Strip Packing". 36th IARCS Annual Conference on Foundations of Software Technology and Theoretical Computer Science (FSTTCS 2016). Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik. 65: 9:1–9:14. doi:10.4230/LIPIcs.FSTTCS.2016.9. S2CID 3205478.
^ Jansen, Klaus; Rau, Malin (29–31 March 2017). "Improved Approximation for Two Dimensional Strip Packing with Polynomial Bounded Width". {WALCOM:} Algorithms and Computation, 11th International Conference and Workshops, {WALCOM} 2017, Hsinchu, Taiwan: 409–420. doi:10.1007/978-3-319-53925-6_32.
^ Baker, Brenda S.; Schwarz, Jerald S. (1 August 1983). "Shelf Algorithms for Two-Dimensional Packing Problems". SIAM Journal on Computing. 12 (3): 508–525. doi:10.1137/0212033. ISSN 0097-5397.
^ Csirik, János; Woeginger, Gerhard J. (28 August 1997). "Shelf algorithms for on-line strip packing". Information Processing Letters. 63 (4): 171–175. doi:10.1016/S0020-0190(97)00120-8. ISSN 0020-0190.
^ Hurink, Johann L.; Paulus, Jacob Jan (2007). "Online Algorithm for Parallel Job Scheduling and Strip Packing". WAOA 2007 - Approximation and Online Algorithms. Lecture Notes in Computer Science. Springer Berlin Heidelberg. 4927: 67–74. doi:10.1007/978-3-540-77918-6_6. ISBN 978-3-540-77917-9.
^ Ye, Deshi; Han, Xin; Zhang, Guochuan (1 May 2009). "A note on online strip packing". Journal of Combinatorial Optimization. 17 (4): 417–423. doi:10.1007/s10878-007-9125-x. ISSN 1573-2886. S2CID 37635252.
^ ^a ^b Han, Xin; Iwama, Kazuo; Ye, Deshi; Zhang, Guochuan (2007). "Strip Packing vs. Bin Packing". Algorithmic Aspects in Information and Management. Lecture Notes in Computer Science. Springer Berlin Heidelberg. 4508: 358–367. arXiv:cs/0607046. doi:10.1007/978-3-540-72870-2_34. ISBN 978-3-540-72868-9. S2CID 580.
^ ^a ^b Seiden, Steven S. (2001). "On the Online Bin Packing Problem". Automata, Languages and Programming. Lecture Notes in Computer Science. Springer Berlin Heidelberg. 2076: 237–248. doi:10.1007/3-540-48224-5_20. ISBN 978-3-540-42287-7.
^ Brown, Donna J.; Baker, Brenda S.; Katseff, Howard P. (1 November 1982). "Lower bounds for on-line two-dimensional packing algorithms". Acta Informatica. 18 (2): 207–225. doi:10.1007/BF00264439. hdl:2142/74223. ISSN 1432-0525. S2CID 21170278.
^ Johannes, Berit (1 October 2006). "Scheduling parallel jobs to minimize the makespan" (PDF). Journal of Scheduling. 9 (5): 433–452. doi:10.1007/s10951-006-8497-6. hdl:20.500.11850/36804. ISSN 1099-1425. S2CID 18819458.
^ Hurink, J. L.; Paulus, J. J. (1 January 2008). "Online scheduling of parallel jobs on two machines is 2-competitive". Operations Research Letters. 36 (1): 51–56. doi:10.1016/j.orl.2007.06.001. ISSN 0167-6377.
^ Kern, Walter; Paulus, Jacob Jan (2009). "A note on the lower bound for online strip packing". Operations Research Letters.
^ Balogh, János; Békési, József; Galambos, Gábor (6 July 2012). "New lower bounds for certain classes of bin packing algorithms". Theoretical Computer Science. 440–441: 1–13. doi:10.1016/j.tcs.2012.04.017. ISSN 0304-3975.
^ Yu, Guosong; Mao, Yanling; Xiao, Jiaoliao (1 May 2016). "A new lower bound for online strip packing". European Journal of Operational Research. 250 (3): 754–759. doi:10.1016/j.ejor.2015.10.012. ISSN 0377-2217.

[1] Wäscher, Gerhard; Haußner, Heike; Schumann, Holger (16 December 2007). "An improved typology of cutting and packing problems". European Journal of Operational Research. 183 (3): 1109–1130. doi:10.1016/j.ejor.2005.12.047. ISSN 0377-2217.

[Baker1980-2] ^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j Baker, Brenda S.; Coffman Jr., Edward G.; Rivest, Ronald L. (1980). "Orthogonal Packings in Two Dimensions". SIAM J. Comput. 9 (4): 846–855. doi:10.1137/0209064.

[Harren-3] Harren, Rolf; Jansen, Klaus; Prädel, Lars; van Stee, Rob (February 2014). "A (5/3 + epsilon)-approximation for strip packing". Computational Geometry. 47 (2): 248–267. doi:10.1016/j.comgeo.2013.08.008.

[4] Neuenfeldt Junior, Alvaro Luiz. "The Two-Dimensional Rectangular Strip Packing Problem" (PDF). 10820228.

[Henning-5] Henning, Sören; Jansen, Klaus; Rau, Malin; Schmarje, Lars (2019). "Complexity and Inapproximability Results for Parallel Task Scheduling and Strip Packing". Theory of Computing Systems. 64: 120–140. arXiv:1705.04587. doi:10.1007/s00224-019-09910-6. S2CID 67168004.

[6] Ashok, Pradeesha; Kolay, Sudeshna; Meesum, S.M.; Saurabh, Saket (January 2017). "Parameterized complexity of Strip Packing and Minimum Volume Packing". Theoretical Computer Science. 661: 56–64. doi:10.1016/j.tcs.2016.11.034.

[MartelloExact-7] Martello, Silvano; Monaci, Michele; Vigo, Daniele (1 August 2003). "An Exact Approach to the Strip-Packing Problem". INFORMS Journal on Computing. 15 (3): 310–319. doi:10.1287/ijoc.15.3.310.16082. ISSN 1091-9856.

[Steinberg-8] Steinberg, A. (March 1997). "A Strip-Packing Algorithm with Absolute Performance Bound 2". SIAM Journal on Computing. 26 (2): 401–409. doi:10.1137/S0097539793255801.

[Coffman1980-9] ^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ^k Coffman Jr., Edward G.; Garey, M. R.; Johnson, David S.; Tarjan, Robert Endre (1980). "Performance Bounds for Level-Oriented Two-Dimensional Packing Algorithms". SIAM J. Comput. 9 (4): 808–826. doi:10.1137/0209062.

[Sleator-10] Sleator, Daniel Dominic (1980). "A 2.5 Times Optimal Algorithm for Packing in Two Dimensions". Inf. Process. Lett. 10: 37–40. doi:10.1016/0020-0190(80)90121-0.

[Golan-11] Golan, Igal (August 1981). "Performance Bounds for Orthogonal Oriented Two-Dimensional Packing Algorithms". SIAM Journal on Computing. 10 (3): 571–582. doi:10.1137/0210042.

[12] Baker, Brenda S; Brown, Donna J; Katseff, Howard P (December 1981). "A 5/4 algorithm for two-dimensional packing". Journal of Algorithms. 2 (4): 348–368. doi:10.1016/0196-6774(81)90034-1.

[Schiermeyer-13] Schiermeyer, Ingo (1994). "Reverse-Fit: A 2-optimal algorithm for packing rectangles". Algorithms — ESA '94. Lecture Notes in Computer Science. Vol. 855. Springer Berlin Heidelberg. pp. 290–299. doi:10.1007/bfb0049416. ISBN 978-3-540-58434-6.

[KenyonRémila-14] Kenyon, Claire; Rémila, Eric (November 2000). "A Near-Optimal Solution to a Two-Dimensional Cutting Stock Problem". Mathematics of Operations Research. 25 (4): 645–656. doi:10.1287/moor.25.4.645.12118. S2CID 5361969.

[15] Harren, Rolf; van Stee, Rob (2009). "Improved Absolute Approximation Ratios for Two-Dimensional Packing Problems". Approximation, Randomization, and Combinatorial Optimization. Algorithms and Techniques, 12th International Workshop, {APPROX} 2009, and 13th International Workshop, {RANDOM} 2009, Berkeley, CA, USA, August 21–23, 2009. Proceedings. 5687: 177–189. Bibcode:2009LNCS.5687..177H. doi:10.1007/978-3-642-03685-9_14.

[16] Jansen, Klaus; Solis-Oba, Roberto (August 2009). "Rectangle packing with one-dimensional resource augmentation". Discrete Optimization. 6 (3): 310–323. doi:10.1016/j.disopt.2009.04.001.

[17] Bougeret, Marin; Dutot, Pierre-Francois; Jansen, Klaus; Robenek, Christina; Trystram, Denis (5 April 2012). "Approximation Algorithms for Multiple Strip Packing and Scheduking Parallel Jobs in Platforms". Discrete Mathematics, Algorithms and Applications. 03 (4): 553–586. doi:10.1142/S1793830911001413.

[18] Sviridenko, Maxim (January 2012). "A note on the Kenyon–Remila strip-packing algorithm". Information Processing Letters. 112 (1–2): 10–12. doi:10.1016/j.ipl.2011.10.003.

[JansenRau2019-19] Jansen, Klaus; Rau, Malin (2019). "Closing the Gap for Pseudo-Polynomial Strip Packing". 27th Annual European Symposium on Algorithms (ESA 2019). Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik. 144: 62:1–62:14. doi:10.4230/LIPIcs.ESA.2019.62. S2CID 24303167.

[20] Jansen, Klaus; Thöle, Ralf (January 2010). "Approximation Algorithms for Scheduling Parallel Jobs". SIAM Journal on Computing. 39 (8): 3571–3615. doi:10.1137/080736491.

[21] Nadiradze, Giorgi; Wiese, Andreas (21 December 2015). "On approximating strip packing with a better ratio than 3/2". Proceedings of the Twenty-Seventh Annual ACM-SIAM Symposium on Discrete Algorithms. Society for Industrial and Applied Mathematics: 1491–1510. doi:10.1137/1.9781611974331.ch102. ISBN 978-1-61197-433-1.

[22] Gálvez, Waldo; Grandoni, Fabrizio; Ingala, Salvatore; Khan, Arindam (2016). "Improved Pseudo-Polynomial-Time Approximation for Strip Packing". 36th IARCS Annual Conference on Foundations of Software Technology and Theoretical Computer Science (FSTTCS 2016). Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik. 65: 9:1–9:14. doi:10.4230/LIPIcs.FSTTCS.2016.9. S2CID 3205478.

[23] Jansen, Klaus; Rau, Malin (29–31 March 2017). "Improved Approximation for Two Dimensional Strip Packing with Polynomial Bounded Width". {WALCOM:} Algorithms and Computation, 11th International Conference and Workshops, {WALCOM} 2017, Hsinchu, Taiwan: 409–420. doi:10.1007/978-3-319-53925-6_32.

[BakerOnline1-24] Baker, Brenda S.; Schwarz, Jerald S. (1 August 1983). "Shelf Algorithms for Two-Dimensional Packing Problems". SIAM Journal on Computing. 12 (3): 508–525. doi:10.1137/0212033. ISSN 0097-5397.

[25] Csirik, János; Woeginger, Gerhard J. (28 August 1997). "Shelf algorithms for on-line strip packing". Information Processing Letters. 63 (4): 171–175. doi:10.1016/S0020-0190(97)00120-8. ISSN 0020-0190.

[26] Hurink, Johann L.; Paulus, Jacob Jan (2007). "Online Algorithm for Parallel Job Scheduling and Strip Packing". WAOA 2007 - Approximation and Online Algorithms. Lecture Notes in Computer Science. Springer Berlin Heidelberg. 4927: 67–74. doi:10.1007/978-3-540-77918-6_6. ISBN 978-3-540-77917-9.

[27] Ye, Deshi; Han, Xin; Zhang, Guochuan (1 May 2009). "A note on online strip packing". Journal of Combinatorial Optimization. 17 (4): 417–423. doi:10.1007/s10878-007-9125-x. ISSN 1573-2886. S2CID 37635252.

[HanOnline-28] Han, Xin; Iwama, Kazuo; Ye, Deshi; Zhang, Guochuan (2007). "Strip Packing vs. Bin Packing". Algorithmic Aspects in Information and Management. Lecture Notes in Computer Science. Springer Berlin Heidelberg. 4508: 358–367. arXiv:cs/0607046. doi:10.1007/978-3-540-72870-2_34. ISBN 978-3-540-72868-9. S2CID 580.

[SeidenOnline-29] Seiden, Steven S. (2001). "On the Online Bin Packing Problem". Automata, Languages and Programming. Lecture Notes in Computer Science. Springer Berlin Heidelberg. 2076: 237–248. doi:10.1007/3-540-48224-5_20. ISBN 978-3-540-42287-7.

[30] Brown, Donna J.; Baker, Brenda S.; Katseff, Howard P. (1 November 1982). "Lower bounds for on-line two-dimensional packing algorithms". Acta Informatica. 18 (2): 207–225. doi:10.1007/BF00264439. hdl:2142/74223. ISSN 1432-0525. S2CID 21170278.

[31] Johannes, Berit (1 October 2006). "Scheduling parallel jobs to minimize the makespan" (PDF). Journal of Scheduling. 9 (5): 433–452. doi:10.1007/s10951-006-8497-6. hdl:20.500.11850/36804. ISSN 1099-1425. S2CID 18819458.

[32] Hurink, J. L.; Paulus, J. J. (1 January 2008). "Online scheduling of parallel jobs on two machines is 2-competitive". Operations Research Letters. 36 (1): 51–56. doi:10.1016/j.orl.2007.06.001. ISSN 0167-6377.

[33] Kern, Walter; Paulus, Jacob Jan (2009). "A note on the lower bound for online strip packing". Operations Research Letters.

[34] Balogh, János; Békési, József; Galambos, Gábor (6 July 2012). "New lower bounds for certain classes of bin packing algorithms". Theoretical Computer Science. 440–441: 1–13. doi:10.1016/j.tcs.2012.04.017. ISSN 0304-3975.

[35] Yu, Guosong; Mao, Yanling; Xiao, Jiaoliao (1 May 2016). "A new lower bound for online strip packing". European Journal of Operational Research. 250 (3): 754–759. doi:10.1016/j.ejor.2015.10.012. ISSN 0377-2217.

[1]

[2]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[3]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[34]

[35]

Search

스트립 패킹 문제

네임스페이스

더

목차

정의

변형

경도

최적 솔루션의 속성

다항 시간 근사 알고리즘

하단 위 왼쪽 정렬(BL)

넥스트핏 감소 높이(NFDH)

퍼스트핏 감소 높이(FFDH)

SF(Split-Fit 알고리즘)

슬레이터 알고리즘

분할 알고리즘(SP)

리버스핏(RF)

스타인버그 알고리즘(ST)

의사-폴리놈 시간 근사 알고리즘

온라인 알고리즘

참조