슈퍼래티스

초층 구조는 두 개 이상의 재료로 구성된 주기적인 구조다.전형적으로 한 층의 두께는 몇 나노미터다.양자점 배열이나 양자선 같은 저차원 구조를 가리킬 수도 있다.

디스커버리

초유래성은 요한슨과 린데가^[1] 특수 X선 회절 패턴을 통해 금광과 팔라듐-코퍼 시스템에 대한 연구 끝에 1925년 초에 발견되었다.현장에서의 추가적인 실험 관측과 이론적 수정은 브래들리와 제이,^[2] 고르스키,^[3] 보렐리우스,^[4] 데흘링거스와 그라프,^[5] 브래그와 윌리엄스와^[6] 베테에 의해 이루어졌다.^[7]이론은 결정 격자의 원자가 질서 없는 상태에서 질서 있는 상태로의 전환에 기초하였다.

기계적 특성

J.S. 쾰러는 이론적으로 탄성 상수가 높고 낮은 재료의 대체(나노) 레이어를 사용함으로써 나노레이어에서 탈구 발생원이 작동할 수 없어 최대 100배까지 내성이 개선된다고 예측했다^[8].

그러한 초밀도 소재의 기계적 경도 증가는 1978년 Lehoczky에 의해 Al-Cu와 Al-Ag에 의해 처음 확인되었고,^[9] 이후 Barnett와 Sproul과^[10] 같은 다른 여러 가지에 의해 하드 PVD 코팅에 의해 확인되었다.

반도체 특성

슈퍼레이티스가 대역 간극이 다른 두 개의 반도체 재료로 만들어지면 각 퀀텀은 구조물을 통해 전하가 흐를 수 있는 조건에 영향을 미치는 새로운 선택 규칙을 잘 설정한다.서로 다른 두 반도체 소재는 서로 교대로 침전되어 성장 방향으로 주기적인 구조를 형성한다.1970년 에사키와 츠의 합성 초박막 제안 이후,^[11] 현재 양자 구조로 불리는 그러한 초미세 반도체의 물리학에서 진보가 이루어졌다.양자 구속의 개념은 고립된 양자 우물 이질구조에서 양자 크기 효과를 관측하게 했으며 터널링 현상을 통한 초유착과 밀접한 관련이 있다.따라서 이 두 가지 사상은 동일한 물리적 기준으로 논의되는 경우가 많지만, 각각 전기와 광학 장치의 응용에 유용한 서로 다른 물리학을 가지고 있다.

반도체 슈퍼래티스 유형

슈퍼래티스 미니밴드 구조는 유형 I, 유형 II 또는 유형 III 중 어느 한 가지 구조 유형에 따라 달라진다.타입 I의 경우 전도 대역의 하단과 발랑스 서브 대역의 상단은 동일한 반도체 층에서 형성된다.타입 II에서 전도 및 발란스 서브밴드는 실제 공간과 상호 공간에서 모두 시차되므로 전자와 홀이 서로 다른 층으로 제한된다.타입 III 슈퍼레이트는 HgTe/CdTe와 같은 반메탈 소재를 포함한다.전도 서브밴드의 하단과 발랑스 서브밴드의 상단은 제1종 슈퍼래티스와 유사한 제3종 슈퍼래티스의 동일한 반도체 레이어에 형성되지만, 제3종 슈퍼래티스의 대역 갭은 반도체에서 제로밴드 갭 소재까지, 음의 대역 갭으로 세미메탈까지 연속적으로 조절할 수 있다.

또 다른 종류의 퀘이페리오디악 초라티스는 피보나찌의 이름을 따서 명명되었다.피보나치 슈퍼라티스는 전자 호핑 전송 또는 현장 에너지가 피보나치 시퀀스로 배열된 두 개의 값을 갖는 1차원 퀘이시 결정으로 볼 수 있다.

반도체 소재

성장 방향(z)을 따라 전도 및 발란스 밴드의 GaAs/AlAs 슈퍼래티트와 잠재적 프로필.

초박막 구조를 만드는 데 사용되는 반도체 재료는 IV, III-V, II-VI 소자 그룹으로 나눌 수 있다.그룹 III-V 반도체(특히 GaAs/AlGaAs_x_1−x)는 광범위하게 연구되어 왔지만, SiGe_x_1−x 시스템과 같은 그룹 IV의 이질구조는 격자 불일치가 크기 때문에 실현하기가 훨씬 더 어렵다.그럼에도 불구하고 서브밴드 구조의 변형변형은 이러한 양자구조에서 흥미롭고 많은 관심을 끌었다.

GaAs/AlAs 시스템에서 GaAs와 AlAs 사이의 격자 상수 차이와 열팽창 계수 차이는 모두 작다.따라서 상온에 남아 있는 스트레인은 상피 성장 온도에서 식힌 후 최소화할 수 있다.GaAs/AlGaAs_x_1−x 재료 시스템을 사용하여 첫 번째 합성 슈퍼레이티스를 실현했다.

그래핀/보론 질화물 시스템은 두 결정이 정렬되면 반도체 슈퍼레이트를 형성한다.그것의 충전 캐리어는 에너지 소모가 거의 없이 전기장에 수직으로 움직인다.h-BN은 그래핀과 비슷한 육각형 구조를 갖고 있다.그 초유대칭은 뒤집어진 대칭을 깨뜨렸다.국지적으로 위상학적 전류는 적용된 전류와 유사하며, 이는 큰 계곡-홀 각도를 나타낸다.^[12]

생산

슈퍼래티스는 다양한 기법을 이용해 만들 수 있지만 가장 흔한 것은 분자 빔 에피택시(MBE)와 스퍼터링이다.이 방법들로, 층들은 단지 몇 개의 원자 스페이스의 두께로 만들어질 수 있다.수퍼래티스를 지정하는 예는 [FeV
₂₀
₃₀]₂₀이다.20 20의 철(Fe)과 30å의 바나듐(V)을 20회 반복하여 총 두께 1000å 또는 100nm의 양층을 기술한다.반도체 슈퍼레이츠를 조작하는 수단으로서의 MBE 기술은 가장 중요하다.MBE 기술 외에도, 금속 유기 화학 증기 증착(MO-CVD)이 InGaAsP 합금처럼 쿼터나리 III-V 복합 반도체로 구성된 초전도체 초박막 개발에 기여했다.새로운 기법으로는 금속-유기 분자 등 초고진공(UHV) 기술을 원천 물질로 하는 가스원 취급 기술과 아르신(AsH
₃)과 인광(PH
₃)과 같은 하이브리드 가스를 이용한 가스원 MBE가 복합적으로 개발되었다.

일반적으로 말하는 MBE는 2진법에서 세 가지 온도(예: 기질 온도, 그룹 III의 소스 재료 온도 및 III-V 화합물의 경우 그룹 V 요소)를 사용하는 방법이다.

생성된 슈퍼레이츠의 구조적 품질은 특성 위성 피크를 포함하는 X선 회절 또는 중성자 회절 스펙트럼을 통해 검증할 수 있다.교번 레이어링과 관련된 다른 효과로는 거대 자기저항, X선 및 중성자 미러에 대한 튜닝 가능한 반사율, 중성자 스핀 양극화, 탄성 및 음향 특성 변화 등이 있다.그 구성요소의 성질에 따라, 슈퍼레이티스는 자기, 광학 또는 반도체라고 불릴 수 있다.

[FeV₂₀₃₀]₂₀ superlattice에서 X선 및 중성자 산란.

미니밴드 구조

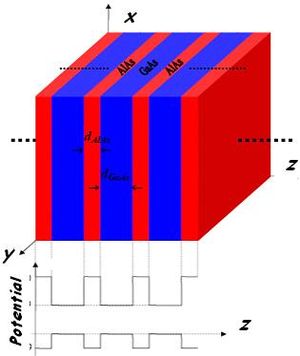
A와 B는 각각 층 두께 a와 b의 반도체 재료(주기: $d=a+b$ = $d=a+b$ + $d=a+b$ $[\displaystyle d=a+b})$ 이다. $d=a+b$ a와 b가 원자간 간격에 비해 너무 작지 않은 경우, 이러한 빠르게 변화하는 전위를 원래의 벌크 반도체의 대역 구조에서 도출된 유효 전위로 교체하여 적절한 근사를 구한다.각각의 개별 계층에서 1D Schrödinger 방정식을 푸는 것은 간단하며, 그 해법 $\psi$ ${\디스플레이$ 스타일 $\psi}$ 은 실제 또는 가상의 지수들의 선형 결합이다 $\psi$ .

큰 장벽 두께의 경우 터널링은 결합되지 않은 분산 상태와 관련하여 약한 동요로, 이 상태 역시 완전히 제한된다.이 경우 산포 관계 $E_{z}(k_{z})$ $E_{z}(k_{z})$ z $E_{z}(k_{z})$ ) ${\displaystyle E_{z}(k_{z})},$ $2\pi /d$ $2\pi /d$ $2\pi /d$ 에 $2 \pi /d$ 걸쳐 주기적이며 $E_{z}(k_{z})$ $d=a+b$ = + $d=a+b$ $d=a+b$ 은 $d=a+b$ 완전히 사인파형이다.

\ E_{z}(k_{z})={\frac {\Delta }{2}}(1-\cos(k_{z}d)}}

유효 질량 변화 부호는 $2\pi /d$ $2\pi /d$ $2\pi /d$ $2\pi /d$ ${\displaystyle 2\pi /d$

\{m^{*}={\frac {\hbar ^{2}}:{2}E/\partial k^{2}} _{k=0}

미니밴드의 경우 이 사인파 문자는 더 이상 보존되지 않는다.미니밴드의 높은 위치에서만 ( $2\pi /d$ 벡터의 경우 2 $[\displaystyle 2\pi/d$ 가 실제로 '분할' 수 있으며, 효과적인 매스 체인지 사인이 된다.미니밴드의 분산 형태는 미니밴드의 운송에 심오한 영향을 미치며, 넓은 미니밴드의 경우 정확한 분산 관계 계산이 필요하다.단일 미니밴드의 운송을 관찰하기 위한 조건은 미니밴드의 간 이전이 어떤 프로세스에 의해서도 없다는 것이다.열 양자 kT는_B 적용된 전기장이 있더라도 첫 번째 미니밴드와 두 번째 미니밴드의 에너지 $E_{2}-E_{1}$ 차이 E $E_{2}-E_{1}$ - $E_{2}-E_{1}$ 1 ${\$ 1}보다 훨씬 작아야 한다.

블로흐 주

이상적인 수퍼래티스의 경우 전체 고유상태 세트는 $e^{i\mathbf {k} \cdot \mathbf {r} }/2\pi$ $e^{i\mathbf {k} \cdot \mathbf {r} }/2\pi$ $e^{i\mathbf {k} \cdot \mathbf {r} }/2\pi$ $e^{i\mathbf {k} \cdot \mathbf {r} }/2\pi$ / $e^{i\mathbf {k} \cdot \mathbf {r} }/2\pi$ 2 $e^{i\mathbf {k} \cdot \mathbf {r} }/2\pi$ $e^{i\mathbf {k} \cdot \mathbf {}/2\pi$ 및 $e^{i\mathbf {k} \cdot \mathbf {r} }/2\pi$ eigen 방정식을 만족하는 $f_{k}(z)$ $f_{k}(z)$ 함수 $f$ k $(z$ )로 구성될 수 있다.

{\displaystyle \left(E_{c}(z)-{\frac {\partial }{\partial z}}{\frac {\hbar ^{2}}{2m_{c}(z)}}{\frac {\partial }{\partial z}}+{\frac {\hbar ^{2}\mathbf {k} ^{2}}{2m_{c}(z)}}\right)f_{k}(z)=Ef_

{k}(z)}

.

As $E_{c}(z)$ and $m_{c}(z)$ are periodic functions with the superlattice period d, the eigenstates are Bloch state $f_{k}(z)=\phi _{q,\mathbf {k} }(z)$ with energy ${\displaystyle E^{\nu }(q,\ma$ $thbf {k$ k의² 1차 섭동 이론 내에서 에너지를 얻는다.

E^{\nu }(q,\mathbf {k} )\approx E^{\nu }(q,\mathbf {0} )+\langle \phi _{q,\mathbf {k} }\mid {\frac {\hbar ^{2}\mathbf {k} ^{2}}{2m_{c}(z)}}\mid \phi _{q,\mathbf {k} }\rangle

.

이제 $\phi _{q,\mathbf {0} }(z)$ $\phi _{q,\mathbf {0} }(z)$ , $\phi _{q,\mathbf {0} }(z)$ ( z $\phi _{q,\mathbf {0} }(z)$ ) ${\displaystyle \phi _{q,\mathbf {$ 0 $} }(z)}$ 은(는) 우물에서 더 큰 확률을 나타낼 것이므로 $\phi _{q,\mathbf {0} }(z)$ , 두 번째 용어를 다음으로 대체하는 것이 타당해 보인다.

E_{k}={\frac {\hbar ^{2}\mathbf {k}^{2}}:{2m_{w}}}}}}}}

여기서 $m_{w}$ $m_{w}$ ${\$ 는 $m_{w}$ 양자 웰의 유효 질량이다.

와니어 함수

정의상, Bloch 함수는 전체 초유래트에 걸쳐 분산된다.이는 전기장을 적용하거나 초저온의 유한한 길이로 인한 영향을 고려할 경우 어려움을 줄 수 있다.따라서 더 잘 현지화된 여러 가지 기본 상태를 사용하는 것이 종종 도움이 된다.유혹적인 선택은 단일 양자 우물의 고유질 사용일 것이다.그럼에도 불구하고 그러한 선택에는 심각한 단점이 있다. 해당 주들은 각각 다른 우물의 존재를 무시한 서로 다른 두 해밀턴인들의 해결책이다.따라서 이러한 상태는 직교하지 않고 합병증을 유발한다.일반적으로 이 접근법에서 이 커플링은 트랜스퍼 해밀턴에 의해 추정된다.이러한 이유로 워니어 기능 세트를 사용하는 것이 더 편리하다.

워니에-스타크 사다리

초밀도 구조물에 전기장 F를 적용하면 해밀턴인은 변환 불변성을 파괴하는 스칼라 전위 eφ(z) = -eFz를 추가로 보이게 된다.In this case, given an eigenstate with wavefunction $\Phi _{0}(z)$ and energy $E_{0}$ , then the set of states corresponding to wavefunctions $\Phi _{j}(z)=\Phi _{0}(z-jd)$ are eigenstates of the Hamiltonian with energies E_j =E₀ − jeFd.이 주들은 에너지와 실제 공간 모두에서 균등하게 간격을 두고 있으며 이른바 워니어-스타크 사다리를 형성하고 있다.잠재적 $\Phi _{0}(z)$ $\Phi _{0}(z)$ ( $\Phi _{0}(z)$ ) $\Phi _{0}(z)$ 은(는) 연속 에너지 스펙트럼을 암시하는 무한 결정(infinite crystal)에 대해 제한되지 않는다 $\Phi _{0}(z)$ .그럼에도 불구하고 이러한 Wannier-Stark 래더의 특성 에너지 스펙트럼은 실험적으로 해결될 수 있다.

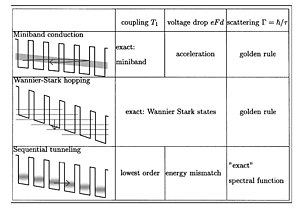
운송

초고속 운송을 위한 다양한 표준 접근법의 개요.

슈퍼레이티스의 충전 캐리어의 동작은 개별 레이어에서의 동작과는 다르다: 충전 캐리어의 이동성이 향상될 수 있어 고주파 소자에 이롭고, 반도체 레이저에 특정한 광학적 특성이 사용된다.

금속이나 반도체와 같은 도체에 외부 바이어스를 적용하면 일반적으로 전류가 발생한다.이 전류의 크기는 재료의 밴드 구조, 산란 과정, 적용된 자기장 강도 및 도체의 평형 캐리어 분포에 의해 결정된다.

초스트라이프라고 불리는 초연속성의 특별한 경우는 스페이서로 분리된 초전도 장치로 만들어진다.각 미니밴드에서 초전도 갭이라고 불리는 초전도 순서 매개변수는 다른 값을 취하여 다중 갭, 또는 2 갭 또는 다중 갭 초전도성을 생성한다.

최근 펠릭스와 페레이라는 피보나치 수열에 따른 그래핀-hBN의 주기적^[13] 및 퀘이페리오다이오드적^[14]^[15]^[16] 슈퍼레이츠에 의한 열수송을 조사했다.퀘이시페리시오드성이 증가함에 따라 일관성 있는 열전달(파동 같은 파동)의 기여가 억제되었다고 보고하였다.

기타 치수

2차원 전자 가스(2DEG)가 일반적으로 실험에 이용 가능하게 된 직후, 연구 단체들은 2D 인공 결정이라고 할 수 있는 구조를^[17] 만들려고 시도했다.아이디어는 두 반도체 사이의 인터페이스(즉, z 방향을 따라)에 국한된 전자를 추가 변조 전위 V(x,y)에 종속시키는 것이다.위에서 설명한 고전적인 수퍼래티스(1D/3D, 3D 벌크 전자 1D 변조)와는 달리, 이는 전형적으로 이단구조 표면(적당한 패턴의 금속 게이트 또는 에칭)을 처리함으로써 달성된다.V(x,y)의 진폭이 큰 경우( $V(x,y)=-V_{0}(\cos 2\pi x/a+\cos 2\pi y/a),V_{0}>0$ , y $V(x,y)=-V_{0}(\cos 2\pi x/a+\cos 2\pi y/a),V_{0}>0$ ) $V(x,y)=-V_{0}(\cos 2\pi x/a+\cos 2\pi y/a),V_{0}>0$ = $V(x,y)=-V_{0}(\cos 2\pi x/a+\cos 2\pi y/a),V_{0}>0$ - V $V(x,y)=-V_{0}(\cos 2\pi x/a+\cos 2\pi y/a),V_{0}>0$ $V(x,y)=-V_{0}(\cos 2\pi x/a+\cos 2\pi y/a),V_{0}>0$ $V(x,y)=-V_{0}(\cos 2\pi x/a+\cos 2\pi y/a),V_{0}>0$ $V(x,y)=-V_{0}(\cos 2\pi x/a+\cos 2\pi y/a),V_{0}>0$ $V(x,y)=-V_{0}(\cos 2\pi x/a+\cos 2\pi y/a),V_{0}>0$ / $V(x,y)=-V_{0}(\cos 2\pi x/a+\cos 2\pi y/a),V_{0}>0$ + $V(x,y)=-V_{0}(\cos 2\pi x/a+\cos 2\pi y/a),V_{0}>0$ $V(x,y)=-V_{0}(\cos 2\pi x/a+\cos 2\pi y/a),V_{0}>0$ $V(x,y)=-V_{0}(\cos 2\pi x/a+\cos 2\pi y/a),V_{0}>0$ $V(x,y)=-V_{0}(\cos 2\pi x/a+\cos 2\pi y/a),V_{0}>0$ y $V(x,y)=-V_{0}(\cos 2\pi x/a+\cos 2\pi y/a),V_{0}>0$ / $V(x,y)=-V_{0}(\cos 2\pi x/a+\cos 2\pi y/a),V_{0}>0$ $V(x,y)=-V_{0}(\cos 2\pi x/a+\cos 2\pi y/a),V_{0}>0$ $V(x,y)=-V_{0}(\cos 2\pi x/a+\cos 2\pi y/a),V_{0}>0$ > $(x,y)=-V_{0}(\cos 2\pi x/a+\cos 2pi y/a),$ $예시$ 로서 $V(x,y)=-V_0(\cos 2\pi x/a+\cos 2\pi y/a), V_0>0$ $V_{0}>0$ }) 페르미 $|V_{0}|\gg E_{f}$ $|V_{0}|\gg E_{f}$ 0 $|V_{0}|\gg E_{f}$ E $|V_{0}|\gg E_{f}$ {\ $displaystyle V_{0} \$ g $E_{f}}$ 에 비교했을 때 $|V_{0}|\gg E_{f}$ 슈퍼래티스의 전자는 정사각형 격자를 가진 원자 결정에서 전자와 비슷하게 동작해야 한다(예시에서는 이러한 "atoms"가 n,m이 정수를 이루는 위치(나, ma)에 위치).

차이점은 길이와 에너지 저울이다.원자 결정의 격자 상수는 1 å의 순서인 반면, 초유성 (a)의 상수는 기술적 한계에 의해 지시된 수 백 또는 수천 개 더 크다(예를 들어, 이질구조 표면의 패터닝에 사용되는 전자 빔 석판술).에너지는 슈퍼레이트에서 그에 상응하여 더 작다.단순한 정렬confined-particle 모델을 사용하여 E1/2{\displaystyle E\propto 1/a^{2}∝}, 현재 국소 graphene(자연의 원자의 결정)과 인공 graphene[18](초격자)과 이 관계는 단지 대강의 지침과 실제 계산 그 특성 밴드 폭이 있다는 것을 보여 줄 것을 제안했다. 1e각각 V와 10meV.약한 변조의 체제( $|V_{0}|\ll E_{f}$ $|V_{0}|\ll E_{f}$ $|V_{0}|\ll E_{f}$ $|V_{0}|\ll E_{f}$ $|V_{0}|\ll E_{f}$ ${\$ 에서는 감응성 진동이나 프랙탈 에너지 스펙트럼(Hofstadter 나비)과 같은 현상이 발생한다. $|V_{0}|\ll E_{f}$

인공 2차원 결정체는 2D/2D 케이스(2D 시스템의 2D 변조)로 볼 수 있으며, 양자선 배열(1D/2D) 또는 3D/3D 광자 결정과 같은 다른 조합을 실험적으로 사용할 수 있다.

적용들

팔라듐-코퍼 시스템의 슈퍼라티스는 고성능 합금에 사용되어 전기 전도도를 높일 수 있으며, 이는 순서가 정해진 구조물이 선호한다.은, 레늄, 로듐, 루테늄과 같은 추가적인 합금 원소들이 더 나은 기계적 강도와 높은 온도 안정성을 위해 첨가된다.이 합금은 프로브 카드의 프로브 바늘에 사용된다.^[19]

참고 항목

참조

^ Johansson; Linde (1925). "The X-ray determination of the atomic arrangement in the mixed-crystal series gold-copper and palladium-copper". Annalen der Physik. 78 (21): 439. Bibcode:1925AnP...383..439J. doi:10.1002/andp.19253832104.
^ Bradley; Jay (1932). "The formation of Superlattices in Alloys if Iron and Aluminium". Proc. R. Soc. A. 136 (829): 210–232. Bibcode:1932RSPSA.136..210B. doi:10.1098/rspa.1932.0075.
^ Gorsky (1928). "X-ray investigations of transformations in the CuAu alloy". Z. Phys. 50 (1–2): 64–81. Bibcode:1928ZPhy...50...64G. doi:10.1007/BF01328593. S2CID 121876817.
^ Borelius (1934). "The theory of transformations of metallic mixed phases". Annalen der Physik. 20 (1): 57. Bibcode:1934AnP...412...57B. doi:10.1002/andp.19344120105.
^ Dehlinger; Graf (1934). "Transformation of solid metal phases I. The tetragonal gold-copper alloy CuAu". Z. Phys. Chem. 26: 343.
^ Bragg, W.L.; Williams, E.J. (1934). "The effect of thermal agitation on atomic arrangement in alloys I". Proc. R. Soc. A. 145 (855): 699–730. Bibcode:1934RSPSA.145..699B. doi:10.1098/rspa.1934.0132.
^ Bethe (1935). "Statistical theory of superlattices". Proc. R. Soc. A. 150 (871): 552–575. Bibcode:1935RSPSA.150..552B. doi:10.1098/rspa.1935.0122.
^ Koehler, J. (1970). "Attempt to Design a Strong Solid". Physical Review B. 2 (2): 547–551. Bibcode:1970PhRvB...2..547K. doi:10.1103/PhysRevB.2.547.
^ Lehoczky, S. L. (1973). "Retardation of dislocation generation and motion in thin-layered metal laminates". Acta Metallurgica. 41 (26): 1814.
^ Yashar, P.; Barnett, S. A.; Rechner, J.; Sproul, W. D. (1998). "Structure and mechanical properties of polycrystalline CrN/TiN superlattices". Journal of Vacuum Science & Technology A: Vacuum, Surfaces, and Films. American Vacuum Society. 16 (5): 2913–2918. Bibcode:1998JVSTA..16.2913Y. doi:10.1116/1.581439. ISSN 0734-2101.
^ Esaki, L.; Tsu, R. (1970). "Superlattice and Negative Differential Conductivity in Semiconductors". IBM Journal of Research and Development. 14: 61–65. doi:10.1147/rd.141.0061.
^ Gorbachev, R. V.; Song, J. C. W.; Yu, G. L.; Kretinin, A. V.; Withers, F.; Cao, Y.; Mishchenko, A.; Grigorieva, I. V.; Novoselov, K. S.; Levitov, L. S.; Geim, A. K. (2014). "Detecting topological currents in graphene superlattices". Science. 346 (6208): 448–451. arXiv:1409.0113. Bibcode:2014Sci...346..448G. doi:10.1126/science.1254966. PMID 25342798. S2CID 2795431.
^ Felix, Isaac M.; Pereira, Luiz Felipe C. (9 February 2018). "Thermal Conductivity of Graphene-hBN Superlattice Ribbons". Scientific Reports. 8 (1): 2737. Bibcode:2018NatSR...8.2737F. doi:10.1038/s41598-018-20997-8. PMC 5807325. PMID 29426893.
^ Felix, Isaac M.; Pereira, Luiz Felipe C. (30 April 2020). "Suppression of coherent thermal transport in quasiperiodic graphene-hBN superlattice ribbons". Carbon. 160: 335–341. arXiv:2001.03072. doi:10.1016/j.carbon.2019.12.090. S2CID 210116531.
^ Felix, Isaac M.; Pereira, Luiz Felipe C. (1 May 2022). "Thermal conductivity of Thue–Morse and double-period quasiperiodic graphene-hBN superlattices". International Journal of Heat and Mass Transfer. Elsevier. p. 122464. doi:10.1016/j.ijheatmasstransfer.2021.122464.
^ Félix, Isaac de Macêdo (4 August 2020). "Condução de calor em nanofitas quase-periódicas de grafeno-hBN" (in Brazilian Portuguese).
^ Heitmann, D.; Kotthaus, J. R. P. (1993). "The Spectroscopy of Quantum Dot Arrays". Physics Today. 46 (6): 56. Bibcode:1993PhT....46f..56H. doi:10.1063/1.881355.
^ Kato, Y.; Endo, A.; Katsumoto, S.; Iye, Y. (2012). "Geometric resonances in the magnetoresistance of hexagonal lateral superlattices". Physical Review B. 86 (23): 235315. arXiv:1208.4480. Bibcode:2012PhRvB..86w5315K. doi:10.1103/PhysRevB.86.235315. S2CID 119289481.
^ "United States Patent US10385424B2 Palladium-based alloys" (PDF). google patents. Retrieved 19 June 2020.

H.T. 그란, "반도체 슈퍼레이츠", 월드 사이언티픽(1995)ISBN 978-981-02-2061-7
Schuller, I. (1980). "New Class of Layered Materials". Physical Review Letters. 44 (24): 1597–1600. Bibcode:1980PhRvL..44.1597S. doi:10.1103/PhysRevLett.44.1597.
모텐 자그드 크리스텐슨, "Epitaxy, Thin Films and Superlatties", Risø 국립 연구소 (1997년).ISBN 8755022987 Google Books 슈퍼래티스 [1]
C. 하마구치, 「반도체 기초 물리학」, 스프링거(2001).구글 북스 ISBN 3540416390 슈퍼래티스
Wacker, A. (2002). "Semiconductor superlattices: A model system for nonlinear transport". Physics Reports. 357 (1): 1–7. arXiv:cond-mat/0107207. Bibcode:2002PhR...357....1W. CiteSeerX 10.1.1.305.3634. doi:10.1016/S0370-1573(01)00029-1. S2CID 118885849.
Haugan, H. J.; Szmulowicz, F.; Mahalingam, K.; Brown, G. J.; Munshi, S. R.; Ullrich, B. (2005). "Short-period InAs/GaSb type-II superlattices for mid-infrared detectors". Applied Physics Letters. 87 (26): 261106. Bibcode:2005ApPhL..87z1106H. doi:10.1063/1.2150269. [2]^{[데드링크]}

추가 읽기

Mendez, E. E.; Bastard, G. R. (1993). "Wannier-Stark Ladders and Bloch Oscillations in Superlattices". Physics Today. 46 (6): 34–42. Bibcode:1993PhT....46f..34M. doi:10.1063/1.881353.

[1] Johansson; Linde (1925). "The X-ray determination of the atomic arrangement in the mixed-crystal series gold-copper and palladium-copper". Annalen der Physik. 78 (21): 439. Bibcode:1925AnP...383..439J. doi:10.1002/andp.19253832104.

[2] Bradley; Jay (1932). "The formation of Superlattices in Alloys if Iron and Aluminium". Proc. R. Soc. A. 136 (829): 210–232. Bibcode:1932RSPSA.136..210B. doi:10.1098/rspa.1932.0075.

[3] Gorsky (1928). "X-ray investigations of transformations in the CuAu alloy". Z. Phys. 50 (1–2): 64–81. Bibcode:1928ZPhy...50...64G. doi:10.1007/BF01328593. S2CID 121876817.

[4] Borelius (1934). "The theory of transformations of metallic mixed phases". Annalen der Physik. 20 (1): 57. Bibcode:1934AnP...412...57B. doi:10.1002/andp.19344120105.

[5] Dehlinger; Graf (1934). "Transformation of solid metal phases I. The tetragonal gold-copper alloy CuAu". Z. Phys. Chem. 26: 343.

[6] Bragg, W.L.; Williams, E.J. (1934). "The effect of thermal agitation on atomic arrangement in alloys I". Proc. R. Soc. A. 145 (855): 699–730. Bibcode:1934RSPSA.145..699B. doi:10.1098/rspa.1934.0132.

[7] Bethe (1935). "Statistical theory of superlattices". Proc. R. Soc. A. 150 (871): 552–575. Bibcode:1935RSPSA.150..552B. doi:10.1098/rspa.1935.0122.

[8] Koehler, J. (1970). "Attempt to Design a Strong Solid". Physical Review B. 2 (2): 547–551. Bibcode:1970PhRvB...2..547K. doi:10.1103/PhysRevB.2.547.

[9] Lehoczky, S. L. (1973). "Retardation of dislocation generation and motion in thin-layered metal laminates". Acta Metallurgica. 41 (26): 1814.

[10] Yashar, P.; Barnett, S. A.; Rechner, J.; Sproul, W. D. (1998). "Structure and mechanical properties of polycrystalline CrN/TiN superlattices". Journal of Vacuum Science & Technology A: Vacuum, Surfaces, and Films. American Vacuum Society. 16 (5): 2913–2918. Bibcode:1998JVSTA..16.2913Y. doi:10.1116/1.581439. ISSN 0734-2101.

[11] Esaki, L.; Tsu, R. (1970). "Superlattice and Negative Differential Conductivity in Semiconductors". IBM Journal of Research and Development. 14: 61–65. doi:10.1147/rd.141.0061.

[12] Gorbachev, R. V.; Song, J. C. W.; Yu, G. L.; Kretinin, A. V.; Withers, F.; Cao, Y.; Mishchenko, A.; Grigorieva, I. V.; Novoselov, K. S.; Levitov, L. S.; Geim, A. K. (2014). "Detecting topological currents in graphene superlattices". Science. 346 (6208): 448–451. arXiv:1409.0113. Bibcode:2014Sci...346..448G. doi:10.1126/science.1254966. PMID 25342798. S2CID 2795431.

[13] Felix, Isaac M.; Pereira, Luiz Felipe C. (9 February 2018). "Thermal Conductivity of Graphene-hBN Superlattice Ribbons". Scientific Reports. 8 (1): 2737. Bibcode:2018NatSR...8.2737F. doi:10.1038/s41598-018-20997-8. PMC 5807325. PMID 29426893.

[14] Felix, Isaac M.; Pereira, Luiz Felipe C. (30 April 2020). "Suppression of coherent thermal transport in quasiperiodic graphene-hBN superlattice ribbons". Carbon. 160: 335–341. arXiv:2001.03072. doi:10.1016/j.carbon.2019.12.090. S2CID 210116531.

[15] Felix, Isaac M.; Pereira, Luiz Felipe C. (1 May 2022). "Thermal conductivity of Thue–Morse and double-period quasiperiodic graphene-hBN superlattices". International Journal of Heat and Mass Transfer. Elsevier. p. 122464. doi:10.1016/j.ijheatmasstransfer.2021.122464.

[16] Félix, Isaac de Macêdo (4 August 2020). "Condução de calor em nanofitas quase-periódicas de grafeno-hBN" (in Brazilian Portuguese).

[17] Heitmann, D.; Kotthaus, J. R. P. (1993). "The Spectroscopy of Quantum Dot Arrays". Physics Today. 46 (6): 56. Bibcode:1993PhT....46f..56H. doi:10.1063/1.881355.

[18] Kato, Y.; Endo, A.; Katsumoto, S.; Iye, Y. (2012). "Geometric resonances in the magnetoresistance of hexagonal lateral superlattices". Physical Review B. 86 (23): 235315. arXiv:1208.4480. Bibcode:2012PhRvB..86w5315K. doi:10.1103/PhysRevB.86.235315. S2CID 119289481.

[19] "United States Patent US10385424B2 Palladium-based alloys" (PDF). google patents. Retrieved 19 June 2020.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[19]

Search