스와인-룹턴 방정식

Swain–Lupton equation

물리적 유기 화학에서, 스와인-럽턴 방정식은 반응 메커니즘의 연구와 유기 화합물에 대한 정량적 구조 활성 관계의 개발에 사용되는 선형 자유 에너지 관계(LFER)이다.그것은 C에 의해 개발되었다.가드너 스웨인과 엘머 C.1968년 Lupton Jr.는 필드 효과와 공명 효과를 모두 포함하기 위해 Hammett 방정식을 개선했다.

배경

유기화학에서 Hammett 그림은 Hammett 방정식 (1)을 사용하여 반응 평형 또는 속도에 대한 치환 효과를 평가할 수 있는 수단을 제공한다.

(1)

해밋은 벤조산과 유도체의 해리에서 얻은 평형 상수로부터 이 방정식을 개발했다(그림 1).

그림 1 치환된 안식향산의 해리

Hammett은 반응 상수())와 치환기 매개변수(σ)의 두 가지 매개변수를 바탕으로 방정식을 정의했다.이러한 매개 변수를 사용하여 다른 반응을 연구했을 때, 치환된 안식향산의 해리 평형에서 이러한 매개 변수의 특정 유도 및 공명 효과의 원래 무시로 인해 항상 상관관계가 발견되지 않았다.따라서 일련의 화합물에 대한 치환기의 영향은 Hammett이 도출한 공명 효과의 방정식을 사용하여 개별 반응 기준으로 연구해야 하지만 둘 다 연구해서는 안 된다.

방정식의 재정의

가드너 스웨인과 엘머 C.Massachusetts Institute of Technology의 Lupton Jr.는 주어진 치환기의 효과를 설명하는 데 두 개 이하의 변수(공진 효과와 전계 효과)가 필요하지 않다는 생각에 기초하여 치환기 매개변수 θ를 재정의했다.필드 효과 F는 모든 효과(유도 및 순수 필드)를 포함하도록 정의된다.마찬가지로, 공명에 의한 영향, R은 전자 기증 능력과 전자 수용 능력의 평균에 기인한다.이 두 가지 효과는 서로 독립적이라고 가정하고 따라서 선형 조합으로 작성할 수 있다.

(2)

Swain과 Lupton이 만든 가정 때문에 이 두 매개변수는 독립된 항으로 취급된다. 치환기는 3개 이상의 포화 중심에서 멀리 떨어져 있거나 치환기가3 3(CH+)N인 경우이다.다른 모든 항은 무시할 수 있으며 스와인-럽턴 방정식 (2)으로 이어진다.

새 대체 매개 변수

치환기 파라미터는 이제 개별 치환기에 따라 달라지는 필드 및 공명 효과 F 및 R에 의해 정의됩니다.상수 r과 f는 두 효과 각각의 중요성을 설명합니다.이러한 상수는 치환기에 의존하지 않고 해밋 치환기 매개변수m(,, ,, ,, , 등pp+') 세트에 의존합니다.

각 치환기 매개변수 세트에 대해 가중 상수 r과 f를 구하기 위해서는 각각의 새로운 치환기 매개변수 θ가X 특정 반응 치환기 매개변수의 선형 조합으로 기록될 수 있다는 사실을 확립해야 한다.

(3)

여기서 θ와1X θ는2X 특정 치환기 매개변수(즉, θ+, θ− 등)이고1 c와2 c는 치환기와 독립적인 상수이다(반응 조건, 즉 온도, 용매 및 연구 대상 개별 반응에 따라 다름).이것은 보다 일반적으로 다음과 같이 표현할 수 있습니다.

(4)

여기서 i는 원점을 (0,0)으로 고정하지 않기 위한 절편입니다.만약 그렇게 하지 않는다면, 이 방정식은 [1]이 방정식을 사용하는 것과 비교하려고 하는 치환되지 않은 화합물에 훨씬 더 많은 무게를 줄 것이다.선형 최소 제곱 분석은 계수/상수 a, b 및 i를 결정하는 데 사용됩니다(스웨인과 Lupton은 DOB: 이중 의무 벡터 [2]평가라는 절차를 사용했습니다).상수는 먼저 앞의 세 가지 반응(,, ,, ),)에mpp+ 기초하였으며, 컴파일된 데이터는 훨씬 더 큰 풀의 최소 조합에 불과하므로 더 많은 오류가 발생할 수 있다.이 제한된 풀에서 발생할 수 있는 오류가 발견되었기 때문에 데이터 풀은 처음부터 규모를 할당하여 증가했습니다.수소는 전기음성도가 비슷해 탄소 원자에 부착했을 때 전자 밀도를 쉽게 기부하거나 받아들이지 않는 것으로 알려져 있기 때문에 제로스케일이 사용된다.이전 연구에서는 이 치환기의 효과가 주로 [3]공진에 의한 것으로 판단되었기 때문에 값 1이 NO에2 할당되었다.마지막으로, 필드 효과를 공명 효과와 직접 비교할 수 있도록 두 구성 요소에 대해 F는 R과 동일하게 설정되었습니다.그 결과 다음과 같은 결과가 초래됩니다.

F = R = H(수소)의 경우 0입니다.
F = R = NO(이산화질소)의2 경우 1.

그림 2는 Swain과 Lupton이 발견한 [2]몇 가지 상대적인 F와 R 값을 보여준다.

대체 카테고리

알킬기는 F에 대해서는 낮은 값에서 0 값을 가지지만 R에 대해서는 적절한 값을 갖습니다.이것은 유도 효과는 거의 또는 전혀 없지만 부분 공명 효과를 의미하는 초결합에 의해 가장 일반적으로 설명된다.

그림 2aF는 일반적인 치환기에 대한 값이다.

CF는3 포합도가 높은 다른 치환기보다 R/F 비율이 훨씬 높다.이것은 Swain에 의해 더 자세히 연구되었지만 여전히 불소화물 과잉 결합으로 가장 잘 설명된다.

그림 2bR은 일반적인 치환기에 대한 값이다.

양전하 치환기(즉,N(CH3)3+과 S(CH3)2+는 문제의 탄소 프레임워크 근처에서 포화 상태인 양의 전하로 인해 더 큰 양의 F 값을 가진다.음전하 치환기(즉, CO와2−3− SO)는 산소 원자 사이의 전자 밀도를 공진시키고 용매와의 수소 결합을 통해 안정화하는 능력 때문에 F 값이 훨씬 낮습니다.

선형 자유 에너지 관계는 한계에 다다랐을 때의 단점에도 불구하고 여전히 유용합니다.스와인-Lupton 치환기 매개변수를 해결하기 위한 새로운 기술은 핵자기공명분광학을 통한 화학적 변화를 연구하는 것이다.최근에는 1,2,3,4,5,6,7,8-옥타히드로아크리딘 및 유도체의 NMR 화학적 이동 및 치환 효과를 연구하였다.-N(COCH)32 그룹에 대해 R 및 F 값이 검색되었습니다.이러한 [4]값은 기존의 방법으로는 찾을 수 없었습니다.

f와 r의 값

r은 반응에 의존하며 모든 치환기에 대해 동일하기 때문에 공진율(%r)을 살펴보는 것이 때때로 유용합니다.

(5)

%r을 사용하여 두 치환기를 비교하는 데이터의 차이를 예측할 수 있다.

(6)

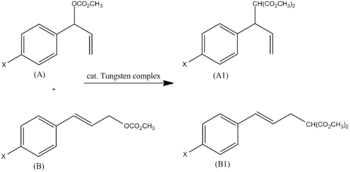
가장 지배적인 효과는 R 대 F의 비율을 보면 명백하다.예를 들어 텅스텐 착체는 알킬화 알릴탄산염 A와 B를 나타낸다.A1과 B1의 비율은 파라 치환기 X에 기인한다(그림3).스와인-Lupton 매개변수(표준 = 0.2F + 0.8R)를 사용하면 -2.5의 µ 값이 기울기로 확인되었다.

그림 3a 탄산염의 알릴화.
그림 3b 스와인-Lupton 매개변수 그래프.

이는 제안된 메커니즘과 일치한다(벤질 탄소에 양전하가 형성되고 공명에 의해 안정화된다. R은 0.8/0.[5]2의 비율로 우세하다).

단점들

확립된 다른 선형 자유 에너지 관계와 마찬가지로, 스와인-럽턴 방정식은 특별한 상황, 즉 메커니즘 또는 용매화 [6]구조의 속도 결정 단계의 변화 발생 시 실패한다.

「 」를 참조해 주세요.

레퍼런스

  1. ^ Swain, C.G; Lupton, E.C., Jr. (1968). "Field and Resonance Components of Substituent Effects". J. Am. Chem. Soc. 90 (16): 4328–4337. doi:10.1021/ja01018a024.{{cite journal}}: CS1 maint: 여러 이름: 작성자 목록(링크)
  2. ^ a b Swain, C.G; Unger, S.H.; Rosenquist, N.R.; Swain, M.S. (1983). "Substituent Effects on Chemical Reactivity. Improved Evaluation of Field and Resonance Components". J. Am. Chem. Soc. 105 (3): 492–502. doi:10.1021/ja00341a032.
  3. ^ Wheland, G.W. (1955). Resonance in Organic Chemistry. New York: Wiley. pp. 367–368. ASIN B00005XST0.
  4. ^ Potmischil, F.; Marinescu, M.; Nicolescu, A.; Deleanu, C.; Hillebrand, M (2008). "Hydroacridines: part 29. 15N NMR chemical shifts of 9-substituted 1,2,3,4,5,6,7,8-octahydroacridines and their N-oxides - Taft, Swain-Lupton, and other types of linear correlations". Magn. Reson. Chem. 46 (12): 1141–1147. doi:10.1002/mrc.2335. PMID 18844244. S2CID 5779503.
  5. ^ Lehman, J.; Lloyd-Jone, G.C. (1995). "Regiocontrol and Stereoselectivity in Tungsten-Bipyridine Catalyzed Allylic Alkylation". Tetrahedron. 51 (32): 8863–8874. doi:10.1016/0040-4020(95)00481-M.
  6. ^ Swain, C.G. (1984). "Substituent and Solvent Effects on Chemical Reactivity". J. Org. Chem. 49 (11): 2005–2010. doi:10.1021/jo00185a035.