Kolsky 기본 모델과 감쇠 및 분산에 대한 수정된 모델

Kolsky 기본 모델과 감쇠 및 분산에 대한 수정된 모델은 지진 애플리케이션에서 가장 많이 사용되는 수학적 Q 모델이다. 기본 Kolsky 모델은 지진 데이터 처리의 단순성에 사용되지만 최소 단계 기준을 엄격하게 충족하지 못하며 Kramers-Kronig 관계를 만족시킬 수 없다. 하지만 그때 콜스키의 변형된 모델은 지진 주파수 대역 내에서 속도 분산을 정확하게 표현하면서 우리를 구하러 왔다. 콜스키의 기본 모델은 구글 책으로 구할 수 있는 콜스키의 책 '고형물에서 스트레스로 웨이브'에 제시되어 있다."고형에서 stress wave in solid."(1963년판) 콜스키의 변형 모델은 왕 작가의 저서 지진 역 Q 필터링에 제시되어 있다. 이 책은 또한 구글 책으로도 이용 가능하다.지진 역 Q 필터링(2008)

기본

수학 Q 모델의 이론적 배경은 위키백과 기사에서 찾을 수 있다. 수학 Q 모델. 여기서 우리는 Futterman에 따라 전파 상수라고 부를 수 있는 기능 K(w)를 발견했다.^[1]

${\displaystyle K(iw)=k(w)+ia(w)\quad(1.3)}$

k(w)는 다음 공식으로 지진파의 위상 속도에 연결할 수 있다.

${\displaystyle c(w)={\frac {w}{k(w)}}\properties(1.4)}$

지진 k(w)에 적용할 수 있는 솔루션을 얻으려면 지진파가 지진 매체에 전파되는 방식을 나타내는 함수에 연결해야 한다. 이 기능은 Q-모델로 간주할 수 있다.

그의 개요에서 왕씨는 콜스키-퓨터맨 모델을 콜스키 모델이라고 부른다. 모델은 감쇠 α(w)가 측정 범위에 걸쳐 주파수에 대해 엄격히 선형이라고 가정한다.^[2]

${\displaystyle \alpha ={\frac {w }{{c_{r}Q_{r}}}}\quad(1.5)}$

그리고 위상 속도를 다음과 같이 정의한다.

${\displaystyle {\frac {1}{c(w)}}={\frac {1}{c_{r}}(1-{\pi Q_{r}}ln {\frac {w}{r}}}}}\quad(1.6)}$

여기서 c와_r Q는_r 위상 속도 및 기준 주파수에서의 Q 값 w이다_r.

Qr >>>1의 큰 값의 경우 용액(1.6)은 대략 다음과 같을 수 있다.

${\displaystyle {\frac {1}{c(w)}={\frac {1}{c_{r}}{\frac {w}{r}} ^{-\fract }\properties (1.7)}$

어디에

${\displaystyle \gamma =(\pi Q_{r})^{-1}$

Kolsky의 모델은 실험적인 관찰로부터 파생되었고 잘 적합되었다. 선형 감쇠 가정을 만족하는 재료 이론의 요건은 기준 주파수 w가_r 흡수 시 유한(임의적으로 작지만 0이 아닌) 컷오프라는 것이다. 콜스키에 따르면 주파수 대역에서 가장 낮은 측정 주파수 w에 비해 작다는 현상학적 기준에 따라 w를_r 자유롭게 선택할 수 있다.^[3] 이 개념에 대한 더 깊은 통찰력을 원하는 사람들은 푸터맨(1962)으로 갈 수 있다.^[4]

연산

Björn Ursin과 Tommy Toverud는 서로 다른 Q 모델을 비교한 기사를 발표했다. 그들은 콜스키 모델을 참조 모델로 사용했다.

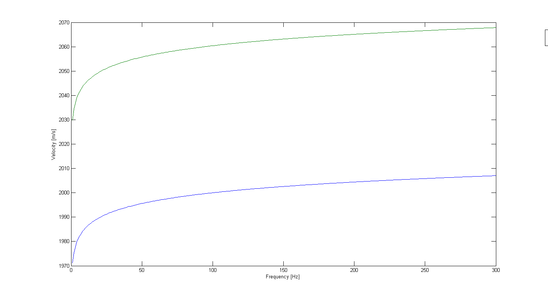
기사에 제시된 Q 모델 각각에 대해, 0–300Hz 주파수 대역의 감쇠(1.5)와 위상 속도(1.6)를 계산했다. 그림_r.1.은 c=2000m/s, Q_r=100, w_r=2π100Hz의 Kolsky 모델 감쇠(왼쪽) 및 위상 속도(오른쪽)에 대한 그래프를 나타낸다.

• 

  그림.1.수화 - 분산 콜스키 모델

w_r 값을 훨씬 더 낮은 값 200.01Hz로 변경하면 모든 주파수에 대해 위상 속도가 더 높아진다.

• 

  그림.2.분산 Kolsky 모델 기준 주파수_r w=2π0.01Hz(녹색) w_r=2π100Hz(파란색)

콜스키 모델 수정

w를_r 주파수 대역에서 가장 낮은 주파수로 선택하면 Kolsky 모델을 역 Q 필터로 사용할 때 위상 오류가 발생한다. 이것은 왕(2008)에 매우 잘 기록되어 있다.^[6] 따라서 기본 Kolsky 모델의 위상 속도 공식은 가장 높은 주파수 w를_h 기준으로 하여 수정된다. 위 Bjørn Ursin과 Tommy Toberud가 사용했던 것과 매우 같을 수 있다, w=2100100_h. Hz. 그러면 우리는 Kolsky 모델로 역 Q 필터링으로 정확한 솔루션을 얻을 수 있다.

메모들

참조

• Wang, Yanghua (2008). Seismic inverse Q filtering. Blackwell Pub. ISBN 978-1-4051-8540-0.
• Kolsky, Herbert (1963). Stress Waves in Solids. Courier Dover Publications. ISBN 9780486495347.