3차원 정격자에서의 다변량 보간법
삼선형 보간은 3차원 정규 그리드에서 다변량 보간 방법이다.격자점의 함수 데이터를 사용하여 로컬 축 직사각형 프리즘 내의 중간 지점 z 값에 근접합니다 .임의의 비구조적 망사(유한 요소 분석에서 사용됨)의 경우 다른 보간 방법을 사용해야 합니다. 모든 망사 요소가 사면체(3D 단순)인 경우, 중심 좌표는 간단한 절차를 제공합니다.
.임의의 비구조적 망사(유한 요소 분석에서 사용됨)의 경우 다른 보간 방법을 사용해야 합니다. 모든 망사 요소가 사면체(3D 단순)인 경우, 중심 좌표는 간단한 절차를 제공합니다.
삼선형 보간은 수치 분석, 데이터 분석 및 컴퓨터 그래픽스에서 자주 사용됩니다.
선형 및 쌍선형 보간과 비교
삼선형 보간은 D { D 인 공간에서 작동하는 선형 보간과 D { D
인 공간에서 작동하는 선형 보간과 D { D 로 작동하는 쌍선형 보간을 D { D=3
로 작동하는 쌍선형 보간을 D { D=3 까지 확장한 것입니다.이러한 보간 방식은 모두 차수 1의 다항식을 사용하여 차수 2의 정확도를 제공하며, 보간 지점 주위에 2 {\ 2}=개의
까지 확장한 것입니다.이러한 보간 방식은 모두 차수 1의 다항식을 사용하여 차수 2의 정확도를 제공하며, 보간 지점 주위에 2 {\ 2}=개의 인접 사전 정의된 값이 합니다.순서 1의 3차원 텐서 B-스플라인 보간과 동일한 3차원 보간법에 도달하는 방법은 여러 가지가 있으며, 3차원 보간 연산자 또한 3개의 선형 보간 연산자의 텐서 곱이다.
인접 사전 정의된 값이 합니다.순서 1의 3차원 텐서 B-스플라인 보간과 동일한 3차원 보간법에 도달하는 방법은 여러 가지가 있으며, 3차원 보간 연산자 또한 3개의 선형 보간 연산자의 텐서 곱이다.
방법

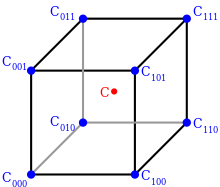
삼선형 보간법의 기하학적 시각화.원하는 지점의 값과 전체 부피의 곱은 각 모서리의 값과 대각선의 반대쪽 부분 부피의 곱의 합과 같다. 주기 및 입방체 격자에서 x  {\
{\ 및 d{\ 는
및 d{\ 는 각각x {\x
각각x {\x {\ y
{\ y {\와
{\와 관련된 작은 좌표의 입니다.
관련된 작은 좌표의 입니다.

서 x 0은
 x({x
x({x 의 격자점을 의
의 격자점을 의 격자점을 나타냅니다. y , , z0({1}
격자점을 나타냅니다. y , , z0({1}  ({
({ 도 입니다.
도 입니다.
먼저 xx})( C_{에
C_{에 의해 정의된 큐브의 면을
의해 정의된 큐브의 면을  에 의해 정의된 반대 면에 "푸시"한다고 가정함)에 따라 보간합니다.
에 의해 정의된 반대 면에 "푸시"한다고 가정함)에 따라 보간합니다.

서 c 000})은 ( , , 0 의 함수값을 의미합니다 (_ { , y _ 0 , y _ 0 , z { } ).} 그런
( , , 0 의 함수값을 의미합니다 (_ { , y _ 0 , y _ 0 , z { } ).} 그런 다음 값(\y
다음 값(\y (\C_
(\C_ })에서 (\displaystyle})
})에서 (\displaystyle}) 로 "푸싱")을 보간하여 다음을 제공합니다
로 "푸싱")을 보간하여 다음을 제공합니다

마지막으로 zz를  다음 값을 보간합니다(직선을 따라 이동).
다음 값을 보간합니다(직선을 따라 이동).

이것으로 점의 예측값을 얻을 수 있습니다.
3선 보간 결과는 3개의 축을 따라 보간 스텝의 순서와 무관합니다. 예를 들어 x y
y  마지막으로 z
마지막으로 z 등의 다른 순서가 동일한 값을 생성합니다.
등의 다른 순서가 동일한 값을 생성합니다.
위의 조작은 다음과 같이 시각화할 수 있습니다.먼저 관심 지점을 둘러싼 큐브의 여덟 모서리를 찾습니다.이러한 모서리에는 c 000 (\100
(\100
 (\{110
(\{110


 의 이 있습니다.displaystyle
의 이 있습니다.displaystyle  를 합니다.
를 합니다.
다음으로 c  과
과
 c 의 선형 보간을 실행하여
c 의 선형 보간을 실행하여 
 c c_101)을
c c_101)을 찾습니다
찾습니다  11
11 c })을
c })을

 하여 10
하여 10 을 검색합니다.
을 검색합니다.
다음으로 c 과 c 에서
c 에서 보간 처리를 하여 0
보간 처리를 하여 0 c({01
c({01 11
11 을
을 마지막으로 값{ c_{ c}를 계산합니다.c 0
마지막으로 값{ c_{ c}를 계산합니다.c 0 ({display0
({display0 }) 1({1})의 선형 으로 }을를) 사용합니다.
}) 1({1})의 선형 으로 }을를) 사용합니다.
실제로, 삼선형 보간은 선형 보간과 결합된 두 개의 쌍선형 보간과 동일합니다.

대체 알고리즘
보간 문제에 대한 해결책을 쓰는 다른 방법은

여기서 계수는 선형 시스템을 풀어서 찾을 수 있다.

결과를 낳다
![{\displaystyle {\begin{aligned}a_{0}={}&{\frac {-c_{000}x_{1}y_{1}z_{1}+c_{001}x_{1}y_{1}z_{0}+c_{010}x_{1}y_{0}z_{1}-c_{011}x_{1}y_{0}z_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}}+{}\\&{\frac {c_{100}x_{0}y_{1}z_{1}-c_{101}x_{0}y_{1}z_{0}-c_{110}x_{0}y_{0}z_{1}+c_{111}x_{0}y_{0}z_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}},\\[4pt]a_{1}={}&{\frac {c_{000}y_{1}z_{1}-c_{001}y_{1}z_{0}-c_{010}y_{0}z_{1}+c_{011}y_{0}z_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}}+{}\\&{\frac {-c_{100}y_{1}z_{1}+c_{101}y_{1}z_{0}+c_{110}y_{0}z_{1}-c_{111}y_{0}z_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}},\\[4pt]a_{2}={}&{\frac {c_{000}x_{1}z_{1}-c_{001}x_{1}z_{0}-c_{010}x_{1}z_{1}+c_{011}x_{1}z_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}}+{}\\&{\frac {-c_{100}x_{0}z_{1}+c_{101}x_{0}z_{0}+c_{110}x_{0}z_{1}-c_{111}x_{0}z_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}},\\[4pt]a_{3}={}&{\frac {c_{000}x_{1}y_{1}-c_{001}x_{1}y_{1}-c_{010}x_{1}y_{0}+c_{011}x_{1}y_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}}+{}\\&{\frac {-c_{100}x_{0}y_{1}+c_{101}x_{0}y_{1}+c_{110}x_{0}y_{0}-c_{111}x_{0}y_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}},\\[4pt]a_{4}={}&{\frac {-c_{000}z_{1}+c_{001}z_{0}+c_{010}z_{1}-c_{011}z_{0}+c_{100}z_{1}-c_{101}z_{0}-c_{110}z_{1}+c_{111}z_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}},\\[4pt]a_{5}=&{\frac {-c_{000}y_{1}+c_{001}y_{1}+c_{010}y_{0}-c_{011}y_{0}+c_{100}y_{1}-c_{101}y_{1}-c_{110}y_{0}+c_{111}y_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}},\\[4pt]a_{6}={}&{\frac {-c_{000}x_{1}+c_{001}x_{1}+c_{010}x_{1}-c_{011}x_{1}+c_{100}x_{0}-c_{101}x_{0}-c_{110}x_{0}+c_{111}x_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}},\\[4pt]a_{7}={}&{\frac {c_{000}-c_{001}-c_{010}+c_{011}-c_{100}+c_{101}+c_{110}-c_{111}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2017eb73468e519de26c930bdde4137584100afb)
「 」를 참조해 주세요.
외부 링크
- (C find Xd, Yd 및 Zd의 정점과 값이 주어짐)는 NASA의 유사 코드이며, 반복적인 역삼선형 보간법을 설명합니다.
- 폴 부르크, 보간법, 1999년이진 논리에 기반하고 모든 차원(테트라리니어, 펜탈리니어 등)으로 확장할 수 있는 3선형 보간을 찾는 매우 영리하고 간단한 방법이 포함되어 있습니다.
- 켄라이트, 자유 형태의 사면체 변형.비주얼 컴퓨팅에 관한 국제 심포지엄.Springer International Publishing, 2015 [1].









 각각
각각

 관련된 작은 좌표의
관련된 작은 좌표의 




 의해 정의된 큐브의 면을
의해 정의된 큐브의 면을 
























![{\displaystyle {\begin{aligned}a_{0}={}&{\frac {-c_{000}x_{1}y_{1}z_{1}+c_{001}x_{1}y_{1}z_{0}+c_{010}x_{1}y_{0}z_{1}-c_{011}x_{1}y_{0}z_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}}+{}\\&{\frac {c_{100}x_{0}y_{1}z_{1}-c_{101}x_{0}y_{1}z_{0}-c_{110}x_{0}y_{0}z_{1}+c_{111}x_{0}y_{0}z_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}},\\[4pt]a_{1}={}&{\frac {c_{000}y_{1}z_{1}-c_{001}y_{1}z_{0}-c_{010}y_{0}z_{1}+c_{011}y_{0}z_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}}+{}\\&{\frac {-c_{100}y_{1}z_{1}+c_{101}y_{1}z_{0}+c_{110}y_{0}z_{1}-c_{111}y_{0}z_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}},\\[4pt]a_{2}={}&{\frac {c_{000}x_{1}z_{1}-c_{001}x_{1}z_{0}-c_{010}x_{1}z_{1}+c_{011}x_{1}z_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}}+{}\\&{\frac {-c_{100}x_{0}z_{1}+c_{101}x_{0}z_{0}+c_{110}x_{0}z_{1}-c_{111}x_{0}z_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}},\\[4pt]a_{3}={}&{\frac {c_{000}x_{1}y_{1}-c_{001}x_{1}y_{1}-c_{010}x_{1}y_{0}+c_{011}x_{1}y_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}}+{}\\&{\frac {-c_{100}x_{0}y_{1}+c_{101}x_{0}y_{1}+c_{110}x_{0}y_{0}-c_{111}x_{0}y_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}},\\[4pt]a_{4}={}&{\frac {-c_{000}z_{1}+c_{001}z_{0}+c_{010}z_{1}-c_{011}z_{0}+c_{100}z_{1}-c_{101}z_{0}-c_{110}z_{1}+c_{111}z_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}},\\[4pt]a_{5}=&{\frac {-c_{000}y_{1}+c_{001}y_{1}+c_{010}y_{0}-c_{011}y_{0}+c_{100}y_{1}-c_{101}y_{1}-c_{110}y_{0}+c_{111}y_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}},\\[4pt]a_{6}={}&{\frac {-c_{000}x_{1}+c_{001}x_{1}+c_{010}x_{1}-c_{011}x_{1}+c_{100}x_{0}-c_{101}x_{0}-c_{110}x_{0}+c_{111}x_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}},\\[4pt]a_{7}={}&{\frac {c_{000}-c_{001}-c_{010}+c_{011}-c_{100}+c_{101}+c_{110}-c_{111}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2017eb73468e519de26c930bdde4137584100afb)


