반입자
Antiparticle| 반물질 |
|---|
 |
입자 물리학에서, 모든 종류의 입자는 질량은 같지만 물리적인 전하(예: 전하)가 반대인 반입자와 연관되어 있습니다.예를 들어, 전자의 반입자는 양전자(반전자라고도 함)이다.전자가 음전하를 띠는 반면 양전자는 양전하를 띠며 특정 유형의 방사성 붕괴에서 자연적으로 생성된다.양전자의 반입자는 전자라는 것 또한 그 반대이다.
광자와 같은 일부 입자는 그들 자신의 반입자이다.그렇지 않으면, 각 반입자 파트너 쌍에 대해 1개가 정상 입자(일반적으로 일상생활에서 상호작용하는 물질에서 발생하는 입자)로 지정된다.다른 하나(일반적으로 접두사 "반(anti-)"이 주어짐)는 반입자로 지정됩니다.
입자-반입자 쌍은 광자를 생성하면서 서로를 전멸시킬 수 있다. 입자와 반입자의 전하가 반대이기 때문에 총 전하가 보존된다.예를 들어, 자연 방사능 붕괴에서 생성된 양전자는 전자와 함께 빠르게 전멸하여 양전자 방출 단층 촬영에서 이용되는 과정인 감마선 쌍을 생성한다.
자연의 법칙은 입자와 반입자에 대해 매우 대칭적이다.예를 들어, 반양성자와 양전자는 수소 원자와 같은 성질을 가진 것으로 여겨지는 반수소 원자를 형성할 수 있다.이것은 왜 빅뱅 이후 물질의 형성이 물질과 반물질의 반반 혼합이 아닌 거의 모든 물질로 이루어진 우주를 만들어냈는지에 대한 의문으로 이어진다.전하 패리티 위반의 발견은 이 문제를 밝히는 데 도움이 되었습니다.원래 완벽하다고 생각되었던 이 대칭은 대략적인 것에 불과합니다.
전하가 보존되기 때문에 같은 전하의 다른 입자를 파괴하거나(예를 들어 반입자가 베타 붕괴나 우주선의 지구 대기와의 충돌에 의해 자연적으로 생성되는 경우 등), 또는 반입자와 그 반입자가 동시에 생성되지 않으면 반입자를 만들 수 없다.e - CERN의 대형 강입자 가속기와 같은 입자 가속기에서 발생할 수 있습니다.
입자와 반입자는 반대 전하를 가지지만, 전기적으로 중성인 입자는 반입자와 같을 필요는 없다.예를 들어, 중성자는 쿼크로 만들어지며, 반중성자와 반중성자는 접촉하면 서로 전멸하기 때문에 서로 구별할 수 있다.그러나 다른 중성 입자는 광자, Z0 보손, γ0
중간자, 그리고 가상의 중력자와 몇몇 가상의 WIMP와 같은 그들만의 대립자입니다.
역사
실험.
1932년 폴 디락의 양전자의 예측 직후 칼 D. 앤더슨은 우주선의 충돌로 이러한 입자가 구름실 안에서 생성된다는 것을 알아냈다. 구름실에서는 움직이는 전자(또는 양전자)가 가스를 통과할 때 흔적을 남기는 입자 검출기이다.입자의 전하 대 질량비는 자기장에서 구름-챔버 트랙의 휘어지는 반지름을 관찰하여 측정할 수 있습니다.양전자는 경로가 구부러진 방향 때문에 처음에는 반대 방향으로 이동하는 전자로 오인되었다.구름실 내의 양전자 경로는 전자와 동일한 나선 경로를 추적하지만 전하 대 질량비는 같지만 전하 대 질량비는 반대이고 따라서 서명된 전하 대 질량비는 반대이기 때문에 자기장 방향에 대해 반대 방향으로 회전한다.
반양성자와 반양성자는 1955년 [1]버클리 캘리포니아 대학에서 에밀리오 세그레와 오웬 체임벌린이 발견했다.그 이후로, 다른 많은 아원자 입자의 반입자가 입자 가속기 실험에서 생성되었다.최근 몇 년 동안, 반물질의 완전한 원자는 전자파 [2]트랩에 모아진 반양전자와 양전자로 조립되었다.
디랙 홀 이론
양자장론의 발달로 많은 교과서에 남아 있지만 반입자를 구멍으로 해석할 필요가 없어졌다.
디락 방정식의 해는 음의 에너지 양자 상태를 포함한다.결과적으로, 전자는 항상 에너지를 방출하고 음의 에너지 상태에 빠질 수 있다.더 나쁜 것은 사용 가능한 음의 에너지 상태가 무한히 많기 때문에 무한한 양의 에너지를 계속 방출할 수 있다는 것입니다.이러한 비물리적인 상황이 일어나는 것을 막기 위해, 디락은 음의 에너지 전자들로 이루어진 "바다"가 우주를 가득 채우고, 이미 낮은 에너지 상태들을 모두 차지하고 있기 때문에, 파울리 배타 원리 때문에, 다른 전자들이 그것들에 떨어질 수 없다고 제안했다.그러나 때때로 이러한 음의 에너지 입자 중 하나가 이 디락 바다에서 상승하여 양의 에너지 입자가 될 수 있습니다.하지만, 그것이 제거되면, 바다에 구멍을 남길 것이고, 그것은 역방향 전하를 가진 양 에너지 전자와 똑같이 작용하게 될 것이다.이 구멍들은 Paul Dirac에 의해 "부정 에너지 전자"로 해석되었고 1930년 그의 논문 "A Theory[4] of Electrons and Hensor"에서 실수로 양성자와 동일시되었다. 하지만, 이러한 "부정 에너지 전자"는 양성자가 아닌 양자로 밝혀졌다.
이 그림은 우주에 무한한 음전하를 내포하고 있는데, 디랙은 이 문제를 알고 있었다.Dirac은 우리가 이것을 무전하의 정상적인 상태로 인식할 것이라고 주장하려고 했다.또 다른 어려움은 전자와 양성자의 질량의 차이였다.디락은 헤르만 바일이 홀 이론이 음전하와 양전하 사이에서 완전히 대칭이라는 것을 증명하기 전까지 이것이 바다와의 전자기 상호작용 때문이라고 주장하려고 했다.디락은 또한 전자와 양성자가 전멸하여 두 개의 광자를 얻는 반응−
e + p+
→ δ
+ δ를
예측했다.그러나 로버트 오펜하이머와 이고르 탐은 이것이 일반적인 물질을 너무 빨리 사라지게 할 것이라는 것을 증명했다.1년 후인 1931년, 디락은 그의 이론을 수정하고 전자와 같은 질량의 새로운 입자, 양전자를 가정했다.다음 해에 이 입자가 발견되면서 그의 이론에 대한 마지막 두 가지 반대가 제거되었다.
디락의 이론에는 우주의 무한 전하 문제가 남아 있다.어떤 보손들은 또한 반입자를 가지고 있지만, 보손들은 파울리 배타원리를 따르지 않기 때문에, 구멍 이론은 그들에게 효과가 없다.양자장 이론에서는 반물질의 통일된 해석을 이용할 수 있는데, 양자장 이론에서는 반물질을 같은 기초 물질장의 음의 에너지 상태, 즉 시간적으로 [5]역행하는 입자로 설명함으로써 이 두 가지 문제를 모두 해결합니다.
입자-반입자 소멸
만약 입자와 반입자가 적절한 양자 상태에 있다면, 그들은 서로를 전멸시키고 다른 입자를 만들어 낼 수 있다.예를 들어+
, e + e → → α
(전자-전자쌍의 2극자 소멸)와 같은−
반응이 있다.전자-전자 쌍 e−
+ e+
→ δ의
단일 입자 전멸은 이 과정에서 에너지와 운동량을 함께 보존하는 것이 불가능하기 때문에 빈 공간에서 발생할 수 없다.그러나 핵의 쿨롱장에서는 변환 불변성이 깨지고 단광자 전멸이 [6]발생할 수 있다.이러한 이유로 (자유 공간에서, 원자핵이 없는) 역반응 또한 불가능하다.양자장 이론에서, 이 과정은 불확실성 원리에 의해 에너지 보존의 위반이 수용될 수 있을 정도로 짧은 시간 동안 중간 양자 상태로만 허용된다.이것에 의해, 1개의 입자 양자 상태가 2개의 입자 상태로 변동해, 다시 돌아올 가능성이 있는 가상 쌍 생성 또는 소멸의 길이 열립니다.이러한 과정은 양자장 이론의 진공 상태와 재규격화에서 중요하다.또한 여기에 나와 있는 것과 같은 과정을 통해 중성 입자가 혼합될 수 있는 길을 열어줍니다. 이것은 질량 재규격화의 복잡한 예입니다.
특성.
입자와 반입자의 양자상태는 C(\C), P(\ P와 T(\T의 조합에 의해 된다.C(\C)와(\P)는 선형, 유니터리 연산자 T이다. 및 ,⟩⟩⟩ - ⟩⟩、 { style T, \ \ T^ { - 1 , \ Psi ( T^ {-1} , \ ) 、의 z방향 컴포넌트가 displaystyle인 경우, 1개는
서 n c{\ n는 전하 공역 상태, 즉 반입자를 나타냅니다.특히 거대한 입자와 그 반입자는 푸앵카레 그룹의 동일한 환원 불가능한 표현 하에서 변환되며, 이는 반입자가 동일한 질량과 동일한 스핀을 갖는다는 것을 의미한다.
C C P 및 T를 파티클과 대립자에 개별적으로 정의할 수 있는
여기서 비례 기호는 오른쪽에 위상이 있을 수 있음을 나타냅니다.
T CPT는 와 반교합하므로 T - Q CPT,Q =- 입자 및 반물질은 서로 반대되는 전하 q와 -q를 가집니다.
양자장론
글을 써서 소멸 연산자와 생성 연산자를 섞지 않고 전자장을 양자화하려고 시도할 수 있다.
여기서 우리는 이전 섹션의 양자수 p와 θ를 나타내기 위해 기호 k를 사용하고 에너지 부호 E(k)와k a는 대응하는 소멸 연산자를 나타낸다.물론 페르미온을 취급하고 있기 때문에 연산자가 표준 반정사 관계를 만족하도록 해야 합니다.하지만, 만약 누군가가 지금 해밀턴을 쓴다면
그러면 H의 기대치가 양수일 필요는 없다는 것을 즉시 알 수 있다.이는 E(k)가 임의의 부호를 가질 수 있고 생성 연산자와 소멸 연산자의 조합에는 기대치가 1 또는 0이기 때문입니다.
따라서 전하공역반입자장을 도입해야 하며, 그 자체 생성 연산자와 소멸 연산자가 관계를 만족시켜야 한다.
여기서 k는 p가 같고, 반대로 θ와 에너지의 부호가 있다.그런 다음 폼에 필드를 다시 쓸 수 있습니다.
여기서 첫 번째 합계는 양의 에너지 상태에 대한 것이고 두 번째 합계는 음의 에너지 상태에 대한 것입니다.그 에너지가
여기서0 E는 무한 음의 상수입니다.진공 상태는 입자 또는 반입자가 없는 상태로 정의됩니다. 즉, \ _ { } \ = \ b { } \ 입니다.그러면 진공의 에너지는 정확히0 E입니다.모든 에너지는 진공에 대해 측정되기 때문에 H는 양의 양이다.a와k b의k 성질을 분석한 결과 하나는 입자의 소멸 연산자이고 다른 하나는 반입자의 소멸 연산자임을 알 수 있다.이것은 페르미온의 경우입니다.
이러한 접근은 Vladimir Fock, Wendell Fulfy 및 Robert Oppenheimer에 의한 것입니다.실제 스칼라 필드를 양자화하면 소멸 연산자는 한 종류뿐이므로 실제 스칼라 필드는 중성 보손을 나타냅니다.복합 스칼라 장은 결합에 의해 관련되는 두 가지 다른 종류의 소멸 연산자를 수용하기 때문에, 그러한 필드는 하전 보손을 기술한다.
파인만-슈투켈베르크 해석
Ernst Stueckelberg는 전자장의 음의 에너지 모드의 시간 역방향 전파를 고려함으로써 입자와 반입자가 같은 질량 m과 스핀 J를 가지지만 반대 전하 q를 갖는다는 사실을 그림적으로 이해했다.이것은 그가 섭동 이론을 도표의 형태로 정확하게 다시 쓸 수 있게 해주었다.리처드 파인만은 나중에 입자 형식주의로부터 독립적으로 계통적으로 이 도표를 도출했고, 그것들은 현재 파인만 도표라고 불립니다.다이어그램의 각 선은 시간 역방향 또는 전방으로 전파되는 입자를 나타냅니다.파인만 다이어그램에서는 반입자가 정상 물질에 대해 시간적으로 역방향으로 이동하는 것을 보여주며,[7] 그 반대도 마찬가지입니다.이 기술은 오늘날 양자장 이론에서 진폭을 계산하는 가장 광범위한 방법입니다.
이 그림은 슈투켈버그에 [8]의해 처음 개발되어 파인만의 [9]작품에서 현대적 형태를 얻었기 때문에, 두 과학자를 기리기 위해 반입자의 파인만-슈투켈버그 해석이라고 불린다.
「 」를 참조해 주세요.
메모들
- ^ "The Nobel Prize in Physics 1959".
- ^ "Antimatter Atoms Trapped for First Time—"A Big Deal"". 19 November 2010.
- ^ Weinberg, Steve (1995-06-30). The quantum theory of fields, Volume 1 : Foundations. pp. 14. ISBN 0-521-55001-7.
- ^ Dirac, Paul (1930). "A Theory of Electrons and Protons". Proceedings of the Royal Society A. 126 (801): 360–365. Bibcode:1930RSPSA.126..360D. doi:10.1098/rspa.1930.0013.
- ^ Lancaster, Tom; Blundell, Stephen J.; Blundell, Stephen (April 2014). Quantum Field Theory for the Gifted Amateur. OUP Oxford. p. 61. ISBN 9780199699339.
- ^ Sodickson, L.; W. Bowman; J. Stephenson (1961). "Single-Quantum Annihilation of Positrons". Physical Review. 124 (6): 1851–1861. Bibcode:1961PhRv..124.1851S. doi:10.1103/PhysRev.124.1851.
- ^ Griffiths, D.J. (2008). Introduction to Elementary Particles (2nd ed.). John Wiley & Sons. p. 61. ISBN 978-3-527-40601-2.
- ^ Stueckelberg, Ernst(1941), "La signation du temps propre en mécanique ondulatoire."헬프, 물리 액타 14, 페이지 322–323.
- ^ Feynman, Richard P. (1948). "Space-time approach to non-relativistic quantum mechanics" (PDF). Reviews of Modern Physics. 20 (2): 367–387. Bibcode:1948RvMP...20..367F. doi:10.1103/RevModPhys.20.367.
레퍼런스
- Feynman, R. P. (1987). "The reason for antiparticles". In R. P. Feynman; S. Weinberg (eds.). The 1986 Dirac memorial lectures. Cambridge University Press. ISBN 0-521-34000-4.
- Weinberg, S. (1995). The Quantum Theory of Fields, Volume 1: Foundations. Cambridge University Press. ISBN 0-521-55001-7.
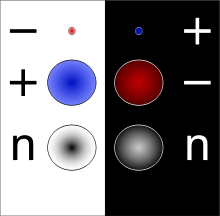





 z방향 컴포넌트가
z방향 컴포넌트가 

 전하 공역 상태, 즉 반입자를 나타냅니다.특히 거대한 입자와 그 반입자는
전하 공역 상태, 즉 반입자를 나타냅니다.특히 거대한 입자와 그 반입자는 













