불확정성원리
Uncertainty principle| 에 대한 일련의 기사의 일부 |
| 양자역학 |
|---|

하이젠베르크의 불확정성 원리라고도 불리는 불확정성 원리는 양자역학의 기본 개념입니다. 위치 및 운동량과 같은 특정 쌍의 물리적 특성을 동시에 알 수 있는 정밀도에는 한계가 있다고 명시되어 있습니다. 즉, 하나의 속성을 정확하게 측정할수록 다른 속성을 덜 정확하게 알 수 있습니다.
보다 형식적으로, 불확정성 원리는 위치, x 및 운동량 p와 같은 양자 시스템에서 특정 관련 측정 쌍의 정확도의 곱에 대한 근본적인 한계를 주장하는 다양한 수학적 부등식 중 하나입니다.[1] 이러한 쌍대 변수는 보완 변수 또는 표준 공액 변수로 알려져 있습니다.
1927년 독일의 물리학자 베르너 하이젠베르크에 의해 처음 소개되었으며, 위치 σ의 표준 편차와 운동량 σ의 표준 편차와 관련된 공식적인 부등식은 그해 말 얼 헤세 케나르에 의해 그리고 1928년 헤르만 바일에 의해 유도되었습니다.
여기서 ℏ =h 2 π{\ \=frac {h}{2\pi}}는 축소된 플랑크 상수입니다.
본질적으로 양자역학적 불확정성 원리는 위치-운동량 외에 다양한 형태로 나타납니다. 에너지-시간 관계는 양자 상태 수명을 측정된 에너지 폭과 관련시키는 데 널리 사용되지만 공식적인 도출은 시간의 본질에 대한 혼란스러운 문제로 가득 차 있습니다. 기본 원리는 여러 방향으로 확장되어 왔고, 여러 종류의 기본적인 물리적 측정에서 고려되어야 합니다.
위치-운동량

이 원리는 인간이 경험하는 거시적[8] 규모에서는 구별할 수 없기 때문에 비교적 쉽게 이해할 수 있는 물리적 상황에 어떻게 적용되는지 설명할 필요가 있습니다. 양자 물리학을 위한 두 가지 대안적인 프레임워크는 불확실성 원리에 대해 서로 다른 설명을 제공합니다. 불확정성 원리의 파동역학 그림은 시각적으로 더 직관적이지만, 추상적인 행렬역학 그림은 더 쉽게 일반화할 수 있는 방식으로 공식화합니다.
수학적으로 파동역학에서 위치와 운동량 사이의 불확실성 관계는 힐베르트 공간에서 대응하는 두 직교 기저에 있는 파동 함수의 표현이 서로의 푸리에 변환이기 때문에 발생합니다(즉, 위치와 운동량은 공액 변수입니다). 0이 아닌 함수와 푸리에 변환은 동시에 급격하게 국소화될 수 없습니다.[9] 푸리에 분석의 밑바탕이 되는 모든 시스템, 예를 들어 음파에서 푸리에 공액의 분산 사이의 유사한 균형이 발생합니다. 순수한 음색은 단일 주파수에서 날카로운 스파이크인 반면 푸리에 변환은 시간 영역에서 음파의 모양을 제공하는데, 이것은 완전히 비국소화된 사인파입니다. 양자역학에서 두 가지 핵심은 입자의 위치가 물질파의 형태를 띠고 운동량은 푸리에 켤레이며, 여기서 k는 파수인 드브로이 관계 p = ħ k에 의해 보장됩니다.
양자 역학의 수학적 공식인 행렬 역학에서는 관측 가능한 것을 나타내는 비통근 자기 인접 연산자 쌍이 유사한 불확실성 한계를 적용받습니다. 관측 가능한 값의 고유 상태는 특정 측정 값(고유 값)에 대한 파동 함수의 상태를 나타냅니다. 예를 들어, 관측 가능한 A의 측정이 수행되면 시스템은 해당 관측 가능한 A의 특정 고유 상태 ψ에 있습니다. 그러나 관측 가능한 A의 특정 고유 상태는 다른 관측 가능한 B의 고유 상태일 필요는 없습니다. 그렇다면 시스템이 해당 관측 가능한 고유 상태에 있지 않기 때문에 고유한 관련 측정값을 갖지 않습니다.[10]
시각화
불확정성 원리는 1차원의 질량을 가진 하나의 스핀이 없는 입자에 대한 위치 및 운동량 공간 파동 함수를 사용하여 시각화할 수 있습니다.
위치-공간 파동함수가 국부화될수록 입자는 해당 영역의 위치 좌표와 함께 발견될 가능성이 높으며, 그에 따라 운동량-공간 파동함수는 덜 국부화되어 입자가 가질 수 있는 운동량 성분이 더 널리 퍼집니다. 반대로, 운동량-공간 파동함수가 국소화될수록 입자는 해당 영역의 운동량 성분 값으로 발견될 가능성이 높으며, 그에 따라 위치-공간 파동함수가 덜 국소화되므로 입자가 차지할 수 있는 위치 좌표는 더 널리 퍼집니다. 이 파동함수들은 서로의 푸리에 변환입니다: 수학적으로, 불확정성 원리는 변환에서 공액 변수들 사이의 관계를 표현합니다.
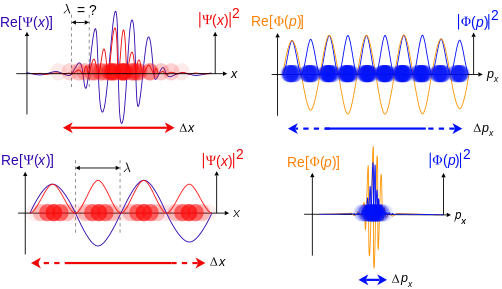
상단: 파장 λ을 알 수 없는 경우 운동량 p, 파동-벡터 k 및 에너지 E(de Broglie 관계)도 마찬가지입니다. 입자가 위치 공간에 더 국한되어 있기 때문에 δx는 δp보다 작습니다.
하단: λ이 알려진 경우 p, k, E도 마찬가지입니다. 입자가 운동량 공간에 더 국한되어 있기 때문에 δp는 δx보다 작습니다.
파동역학 해석
드브로이 가설에 따르면, 우주의 모든 물체는 파동과 연관되어 있습니다. 따라서 기본 입자에서 원자, 분자, 행성과 그 너머에 이르기까지 모든 물체는 불확정성 원리의 적용을 받습니다.
파수 k 또는0 운동량 p의0 단일 모드 평면파의 시간에 독립적인 파동함수는
Born 규칙은 이것이 a와 b 사이의 입자를 발견할 확률이 다음과 같은 의미에서 확률 밀도 진폭 함수로 해석되어야 한다고 말합니다.
단일 모드 평면파의 경우 = x {\ X= x}인 경우ψ ( 2 \psi(x)^{2}}은 1이고, 그렇지 않은 경우 0입니다. 즉, 입자 위치는 본질적으로 파동 패킷을 따라 어디에 있을 수 있다는 점에서 매우 불확실합니다.
반면에, 우리가 다음과 같이 쓸 수 있는 많은 파동들의 합인 파동함수를 생각해 보자.
위치와 운동량의 정밀도를 정량화하는 한 가지 방법은 표준 편차 σ입니다. ψ(x 2 \psi 2}}는 위치에 대한 확률 밀도 함수이므로 표준 편차를 계산합니다.
많은 평면파를 사용함으로써 위치의 정밀도가 향상됩니다. 즉, σ이 감소하여 운동량의 정밀도가 약화됩니다. 즉, σ이 증가합니다. 이를 설명하는 또 다른 방법은 σ와 σ가 역의 관계를 가지거나 적어도 아래로부터 경계가 있다는 것입니다. 이것이 불확정성 원리이며, 그 정확한 한계는 케너드 한계입니다.
다음과 같이 정의되는 위치와 운동량의 분산에 관심이 있습니다.
일반성을 잃지 않고 평균이 사라진다고 가정할 것이며, 이는 좌표의 원점을 이동시키는 것에 불과합니다. (이러한 가정을 하지 않는 보다 일반적인 증거는 아래에 제시되어 있습니다.) 이것은 우리에게 더 간단한 형태를 제공합니다.
( x = x⋅ ψ (x) {\(x) = x\ psi (x)}는 함수 공간의 벡터로 해석할 수 있습니다. 우리는 이 벡터 공간에서 한 쌍의 함수 u(x)와 v(x)에 대한 내적을 정의할 수 있습니다.
이 내부 제품을 정의하면 위치에 대한 분산을 다음과 같이 쓸 수 있습니다.
함수 ~( = ⋅ φ ) )=p \p)}를 벡터로 해석하여 운동량에 대해 이를 반복할 수 있지만, ψ (x) psi (x)}와 φ ( {\displaystyle \varphi(p)}가 서로 푸리에 변환이라는점도 이용할 수 있습니다. 우리는 부품별 통합을 통해 역 푸리에 변환을 평가합니다.
코시-슈바르츠 부등식은 다음과 같이 주장합니다.
임의의 복소수 z의 모듈러스 제곱은 다음과 같이 나타낼 수 있습니다.
이제 이러한 내부 제품을 평가하는 것만 남았습니다.
이것을 위의 부등식에 끼워 넣으면, 우리는
p와 x가 선형 의존적인 경우에만 동일한 값을 갖습니다. 이 증명에 관련된 유일한 물리학은ψ (x) psi(와φ (p) varphi(p)}가 서로의 푸리에 변환인 위치와 운동량에 대한 파동 함수라는 것입니다. 유사한 결과는 모든 공액 변수 쌍에 대해 성립합니다.
행렬역학 해석
(참고)
행렬 역학에서 위치와 운동량과 같은 관측 가능한 것은 자기 인접 연산자로 표현됩니다. 관측 가능한 쌍을 고려할 때 중요한 양은 정류자입니다. 연산자 â 및 쌍의 경우해당 정류자를 다음과 같이 정의합니다.
비상호성의 물리적 의미는 정류자가 위치 및 운동량 고유 상태에 미치는 영향을 고려하여 이해할 수 있습니다. ψ ⟩{\psi\rangle }을(를) 일정한 고유값 x를 갖는 오른쪽 고유 위치 상태라고 합니다. 는 정의에 따라 x ψ ⟩ = 0 ψ ⟩을 합니다 {\hat {x} \psi= x_{0} \psi \ ψ ⟩ {\displaystyle \psi \rangle }에 하면 다음과 같은 결과가 나옵니다.
모순에 의한 증명을 위해 ψ ⟩ {\rangle}도 고유값 p가 일정한 오른쪽 고유 운동량 상태라고 가정해 보겠습니다. 이것이 사실이라면, 누군가는 글을 쓸 수 있을 것입니다.
상태가 측정되면 관련 관측치를 기반으로 고유 상태에 투영됩니다. 예를 들어 입자의 위치를 측정하면 상태는 위치 고유 상태에 해당합니다. 이는 상태가 운동량 고유 상태가 아니라 여러 운동량 기반 고유 상태의 합으로 표현될 수 있음을 의미합니다. 즉, 모멘텀이 덜 정확해야 합니다. 이 정밀도는 표준 편차로 정량화할 수 있습니다.
위의 파동역학 해석에서와 같이, 불확실성 원리에 의해 정량화된 둘 각각의 정밀도 사이의 균형을 볼 수 있습니다.
예
(참조)
양자 고조파 발진기 정지 상태
1차원 양자 고조파 발진기를 생각해 보세요. 생성 및 소멸 연산자의 관점에서 위치 및 운동량 연산자를 표현할 수 있습니다.
에너지 고유 상태에 대한 생성 및 소멸 연산자에 대한 표준 규칙을 사용하면,
특히, 위 케너드 바운드는 기저 상태 n=0에 대해 포화 상태이며, 이 경우 확률 밀도는 정규 분포에 불과합니다.
가우시안 초기 조건을 갖는 양자 고조파 발진기
특징적인 각 주파수 ω의 양자 고조파 발진기에서 전위의 바닥으로부터 어떤 변위 x만큼 오프셋된 상태를 다음과 같이 배치합니다.
관계로부터.
코히어런트 상태
코히어런트 상태는 소멸 연산자의 오른쪽 고유 상태입니다.
양자 고조파 발진기에서 코히어런트 상태가 거대한 입자인 그림에서 위치 및 운동량 연산자는 위의 동일한 공식에서 소멸 연산자로 표현되어 분산을 계산하는 데 사용될 수 있으며,
상자 안의 입자
길이 L인 1차원 상자 안의 입자를 생각해 보자 위치와 운동량 공간의 고유 함수는
따라서 표준 편차의 곱은 다음과 같습니다.
정운동량

어떤 입자가 처음에 어떤 일정한 운동량 p 주위의0 정규분포로 기술되는 운동량 공간 파동함수를 가지고 있다고 가정해 보자.
⟨t) ⟩ = 0 lang p(= p_{0}} 및 σ( = ℏ / x 0) {\ \sigma _pt) =\hbar / ({\sqrt {2}}x_{0}}}이므로, 이는 입자가 임의로 높은 정밀도로 일정한 운동량을 따라 이동하는 것으로 해석할 수 있습니다. 반면에 위치의 표준편차는
에너지-시간 불확정성 원리
에너지 스펙트럼 선폭 대 수명
에너지-시간 불확실성 관계는 다음과 같습니다.
원칙의 비공식적이고 발견적인 의미는 다음과 같습니다.[18]짧은 시간 동안만 존재하는 상태는 확실한 에너지를 가질 수 없습니다. 확실한 에너지를 갖기 위해서는 상태의 주파수가 정확하게 정의되어야 하며, 이를 위해서는 상태가 필요한 정확도의 역수인 많은 주기 동안 서성여야 합니다. 예를 들어, 분광학에서 여기 상태는 유한한 수명을 갖습니다. 시간-에너지 불확정성 원리에 의해, 그들은 확실한 에너지를 가지고 있지 않으며, 그들이 붕괴할 때마다 방출하는 에너지는 약간 다릅니다. 나가는 광자의 평균 에너지는 상태의 이론 에너지에서 피크를 갖지만, 분포는 자연 선폭이라는 유한한 폭을 갖습니다. 빠르게 붕괴하는 상태는 선폭이 넓은 반면 느리게 붕괴하는 상태는 선폭이 좁습니다.[19] 또한 동일한 선폭 효과는 입자 물리학에서 불안정하고 빠르게 붕괴하는 입자의 나머지 질량을 지정하는 것을 어렵게 만듭니다. 입자의 붕괴 속도가 빠를수록(수명이 짧을수록) 입자의 질량은 확실하지 않습니다(입자의 폭이 클수록).
양자역학에서의 시간
양자역학에서 '시간'의 개념은 많은 도전을 제공합니다.[20] 시간 측정의 양자 이론은 없습니다. 상대성 이론은 시간에 대한 기본이고 양자역학에 포함시키기 어렵습니다.[12] 위치와 운동량은 단일 입자와 연관되어 있지만, 시간은 시스템 특성으로 로버트슨-슈뢰딩거 관계에 필요한 연산자가 없습니다.[1] 안정적인 양자 시스템과 불안정한 양자 시스템의 수학적 처리는 다릅니다.[21] 이러한 요소들이 결합하여 에너지-시간 불확실성 원칙을 논란거리로 만듭니다.
"시간"의 세 가지 개념은 외부적, 내재적, 관찰 가능한 것으로 구분할 수 있습니다.[12] 외부 또는 실험실 시간은 실험자가 볼 수 있습니다. 고유 시간은 시계의 손이나 자유 입자의 움직임과 같은 동적 변수의 변화에 의해 추론됩니다. 관찰 가능한 시간은 관찰 가능한 시간, 시간 분리된 이벤트의 측정에 관한 것입니다.
외부 시간 불확정성 원리는 양자계의 에너지를정확도로 측정하기 위해서는 시간δ t > h /δ delta t > h/\delta E}가 필요하다고 말할 수 있습니다. 그러나 야키르 아하로노프와 데이비드 봄은 일부 양자계에서 에너지는 임의의 짧은 시간 내에 정확하게 측정될 수 있습니다. 외부 시간 불확실성 원리는 보편적이지 않습니다.
고유 시간은 Mandelstam을 포함한 에너지-시간 불확실성 관계의 여러 공식화의 기초입니다.탐 관계는 다음 절에서 논의합니다. 외부 실험실 시간과 밀접하게 일치하는 고유 시간을 가진 물리적 시스템을 "시계"라고 합니다.[20]: 31
두 사건 사이의 시간을 측정하는 관찰 가능한 시간은 양자 이론의 과제로 남아 있습니다. 양의 연산자 값 측정 개념을 사용하여 일부 진전이 이루어졌습니다.[12]
만델스탐-탐
1945년 레오니드 만델스탐과 이고르 탐은 비상대론적 시간-에너지 불확정성 관계를 다음과 같이 도출했습니다.[23][12] 하이젠베르크 역학에서, 자기 인접 연산자 로 표현되는 명시적인 시간 의존성이 없는 관측 가능한 B에 대한 일반화된 에렌페스트 정리는 의 평균값의 시간 의존성을 해밀턴과의 정류자의 평균과 연관시킵니다.
⟨[ ⟩ {H}}, {\B}},\nangle } 값은 에너지 H^ H}} 및 B^ hat {B}}에 대한 로버스턴 불확실성 관계에 대입됩니다.
- 자유 양자 입자가 공간의 한 점을 통과하는 시간은 상태의 에너지가 더 정밀하게 제어됨에 따라 더 불확실합니다. δ T =ℏ / 2 δ E. {\=hbar / 2\Delta E.} 시간 스프레드는 입자 위치 스프레드와 관련이 있고 에너지 스프레드는 운동량 스프레드와 관련이 있기 때문에, 이 관계는 위치-momentum 불확실성과 직접적으로 관련이 있습니다.
- 양성자와 중성자와 관련된 쿼크의 준안정성 복합체인 델타 입자의 수명은 10초이므로−23 에너지와 동등한 측정 질량인 1232 MeV/c는2 ±120 MeV/c만큼2 변합니다. 이 변화는 본질적인 것이며 측정 오류로 인해 발생한 것이 아닙니다.[25]: 144
- 두 개의 에너지 상태ψ 1, 2_{1, 2 E 1 2, {\E_{1, 2}}를 중첩하여 복합 상태를 만듭니다.
- 이 상태의 확률 진폭은 시간 의존적 간섭 항을 갖습니다.
- 발진 주기는 에너지 차이(τ = 2π ℏ /(E2 - E 1) \tau =2 (E_{2}-E_{1})}에 따라 반비례합니다.
각 예제는 사용된 관측 가능한 상태와 상태에 따라 시간 불확실성에 대해 다른 의미를 갖습니다.
양자장이론
양자장 이론의 일부 공식은 가상 입자라고 불리는 계산에서 일시적인 전자-양전자 쌍을 사용합니다. 이 입자들의 질량 에너지와 수명은 에너지-시간 불확실성 관계에 의해 연관됩니다. 양자계의 에너지는 그들의 행동을 하나의 단순한 역사로 제한할 만큼 충분히 정확하게 알려져 있지 않습니다. 따라서 모든 역사의 영향은 측정/계산된 에너지 분포의 평균보다 훨씬 크거나 적은 에너지를 가진 역사를 포함하여 양자 계산에 통합되어야 합니다.
에너지-시간 불확정성 원리는 에너지 보존을 일시적으로 위반하는 것이 아니라, 짧은 시간 내에 에너지가 '돌아온' 한 우주로부터 '빌려온' 것을 의미하는 것이 아닙니다.[25]: 145 우주의 에너지는 항상 정확히 알려진 매개변수가 아닙니다.[1] 사건이 매우 짧은 시간 간격으로 발생하면 이러한 사건의 에너지에 불확실성이 있습니다.
고유양자불확실성
역사적으로, 불확정성 원리는 관측자 효과라고 불리는 물리학의 관련 효과와 혼동되어[26][27] 왔습니다. 관측자 효과는 특정 시스템의 측정이 시스템에 영향을 미치지 않고,[28][29] 즉 시스템의 어떤 것을 변경하지 않고는 이루어질 수 없다는 것에 주목합니다. 하이젠베르크는 양자적 불확실성에 대한 물리적 "설명"[30]으로 양자 수준에서 이러한 관찰자 효과를 사용했습니다. 그러나 불확정성 원리는 모든 파동과 같은 시스템의 특성에 내재되어 있으며,[31] 단지 모든 양자 물체의 물질파 특성 때문에 양자역학에서 발생한다는 것이 더 명확해졌습니다.[32] 따라서 불확정성 원리는 실제로 양자 시스템의 근본적인 속성을 나타내며 현재 기술의 관찰 성공에 대한 진술이 아닙니다.[33]
수학적 형식주의
Kennard의 위치-운동량 불확실성 도출을 시작으로 Howard Percy Robertson은 표준 편차로 표현되는 임의의 에르미트 연산자 O 에 대한 공식을 개발했습니다[34][1].
로버트슨 불확실성 관계는 다음과 같습니다.
에드윈 슈뢰딩거.[35] Robertson-Schrödinger 불확정성 관계로 알려진 더 강한 부등식을 제공하면서 연산자 간의 상관관계를 허용하는 방법을 보여주었습니다.[36][1]
여기서 안티커뮤터 B = B + {\B}}\}={\가 사용됩니다.
여기에 표시된 파생물은 Robertson,[34] Schrödinger[36] 및 Griffiths와 같은 표준 교과서에 표시된 파생물을 통합하고 구축합니다.[25]: 138 임의의 에르미트 연산자 에 대하여 분산의 정의에 기초하여, 우리는
마찬가지로, 동일한 상태에 있는 다른 에르미트 연산자 에 대해서도
따라서 두 편차의 곱은 다음과 같이 표현할 수 있습니다.
-
(1)
벡터 ⟩ f 와 ⟩g\rangle }를 연관시키기 위해 다음과 같이 정의되는 코시-슈바르츠 부등식을 사용합니다.
-
(2)
⟨∣⟩ \langle f\mid g\rangle }는 일반적으로 복소수이므로, z {\ z}의 모듈러스 은z 2 =∗ {\displaystyle z^{2}=z^{*}로 된다는 사실을 사용합니다. 여기서 ∗ {\z^{*}는 zz}의 복소입니다. 모듈러스 제곱은 다음과 같이 표현할 수도 있습니다.
-
(3)
는 = ⟨ ∣ g ⟩ {\z =\ g 및 z ∗ = ⟨g∣ ⟩ {\displaystyle z^{*}=\mid leg\mid f\rangle }를 위 식을 대입하여 구합니다.
-
(4)
내부 ⟨ ∣g ⟩ {\\langle f\mid g\rangle }는 명시적으로 다음과 같이 기재됩니다.
하게 ⟨ g ∣ ⟩ =⟨ ^ A ^ ⟩ - ⟨ ^ ⟩ ⟨ B ^ ⟩를 보여줍니다.langmid =\langhat {hat {A}}\rangle -\hat {A}\rangle \rangle {\hat {B}\rangle}
그래서 우리는
이제 위의 두 방정식을 다시 식 (4)에 대입하여 구합니다.
위의 내용을 식 (2)에 대입하면 슈뢰딩거 불확정성 관계를 얻을 수 있습니다.
이 증명에는 관련된 운영자의 도메인과 관련된 문제가[38] 있습니다. 증명이 의미를 가지려면 벡터 ψ⟩ {\{\ {B \Psi \rangle}이가) A^{\hat {A}}의 도메인에 있어야 하지만 항상 그렇지는 않습니다. A 이 각도 이고 B 이 이 변수에 대한 도함수이면 Robertson 불확실성 관계는 거짓입니다. 이 예제에서 정류자는 하이젠베르크 불확정성 관계에서와 같이 0이 아닌 상수이지만 불확정성의 곱이 0인 상태도 있습니다([39]아래의 반례 참조). 이 문제는 증명을 위해 변형 방법을 [40][41]사용하거나 표준 정류 관계의 지수화된 버전으로 작업하여 극복할 수 있습니다.[39]
로버트슨-슈뢰딩거 불확실성 관계의 일반적인 형태에서는 연산자 및 가 자기 인접 연산자라고 가정할 필요가 없습니다. 그들은 단지 대칭 연산자라고 가정하기에 충분합니다. (이 두 개념의 구별은 일반적으로 물리학 문헌에서 호도되며, 여기서 에르미트라는 용어는 연산자의 둘 중 하나 또는 둘 다에 사용됩니다. 이 중요하지만 기술적인 차이에 대한 자세한 논의는 홀의[42] 책 제9장을 참조하십시오.)
혼합 상태
로버트슨-슈뢰딩거 불확실성 관계는 혼합 상태를 설명하는 간단한 방법으로 일반화될 수 있습니다.
Maccone-Pati 불확실성 관계
로버트슨-슈뢰딩거 불확실성 관계는 시스템의 상태가 관측 가능한 상태 중 하나의 고유 상태로 선택되면 사소할 수 있습니다. 로렌조 매콘과 아룬 K가 증명한 더 강력한 불확실성 관계. 파티는 양립할 수 없는 두 관측치에 대한 분산의 합에 대한 사소하지 않은 경계를 제공합니다.[43] (분산의 합으로 공식화된 불확실성 관계에 대한 이전 연구에는 [44]예를 들어 Yichen Huang의 Ref가 포함됩니다.) 두 개의 비통근 관측치 A B 에 대해 첫 번째로 더 강한 불확실성 관계는 다음과 같습니다.
두 번째로 강한 불확실성 관계는 다음과 같습니다.
밀도행렬의 분해를 바탕으로 한 로버트슨-슈뢰딩거 불확실성 관계 개선
Robertson-Schrödinger 불확실성은 다음과 같이 주어진 밀도 행렬의 모든 분해에서 k \{k}}ϱ 모든 구성 요소에 대해 유지되어야 한다는 점에 주목하여 개선될 수 있습니다.
유사한 인수를 사용하면 오른쪽에[45] 볼록한 지붕이 있는 관계를 도출할 수 있습니다.
볼록한[48] 지붕이 없으면 더 간단한 부등식이 뒤따릅니다.
위상공간
양자역학의 위상 공간 공식에서 로버트슨-슈뢰딩거 관계는 실제 별-제곱 함수의 양의 조건에서 따릅니다. 스타 제품 ★ 및 함수 f를 갖는 위그너 W p가 주어졌을 때, 일반적으로 다음과 같습니다.
= + b + f = + + 를 선택하면 다음과 같습니다
이 양의 조건은 모든 a, b, c에 대해 참이므로 행렬의 모든 고유값은 음수가 아닙니다.
음이 아닌 고유값은 행렬식에서 해당하는 음이 아닌 조건을 의미합니다.
예
Robertson과 Schrödinger 관계는 일반 연산자를 대상으로 하므로 특정 불확실성 관계를 얻기 위해 두 관측값에 관계를 적용할 수 있습니다. 문헌에서 발견되는 가장 일반적인 관계는 다음과 같습니다.
- 위치-선형 운동량 불확정성 관계: 위치 및 선형 운동량 연산자에 대한 표준 정류 관계[ p = ℏhat { {\hat {p}}, =i\hbar}는 위의 케너드 부등식을 의미합니다.
- 각운동량 불확실성 관계: 물체의 총 각운동량 연산자의 두 직교 성분의 경우: 여기서 i, j, k는 구별되고, J는i x축에i 따른 각운동량을 나타냅니다. 이 관계는 세 가지 구성 요소가 모두 함께 사라지지 않는 한 시스템의 각운동량의 단일 구성 요소, 일반적으로 외부(자기 또는 전기) 필드와 평행한 구성 요소만 임의의 정밀도로 정의할 수 있음을 의미합니다. 또한 ] = ℏ ε z z {\J_{x}의 경우, a choice , , in angular momentum multiplets, ψ = j, m⟩, bounds the Casimir invariant (angular momentum squared, 아래로부터의 따라서 j(j + 1) m(m + 1), 따라서 j m 등과 같은 유용한 제약 조건을 생성합니다.
- 초전도체의 전자 수와 긴즈부르크-란다우 순서 매개변수의[50][51] 위상에 대하여
한계
The derivation of the Robertson inequality for operators and requires and to be defined. 이러한 조건이 유효하지 않은 양자 시스템이 있습니다.[52] 한 예로 링 위의 양자 입자를 들 수 있는데, 여기서 파동함수는 [ 2 π 0, 2\pi]} 의 각도 가변θ \theta }에 따라 달라집니다. "위치" 및 " A^ {\hat}} B^{\hat {B}}를 다음과 같이 정의합니다.
이제ψ \psi }을(를) B^ {\hat {B}}의 중 하나라고 가정합니다. 이 상태는θ {\ \psi(\theta)=e^{2\pi in\theta}의 ψθ =e^{2\pi)로됩니다. 이러한 상태는 라인의 운동량 연산자의 고유 상태와 달리 정규화할 수 있습니다. 연산자 은는) 경계 구간에 걸쳐 있기 때문에 θ자 A^ {\displaystyle{\hat {A}}이(가) 경계입니다. 따라서 상태ψ\psi}에서 B B}의불확실성은 0이고 A A}의은 유한하므로,
실제 라인의 일반적인 및 운동량 연산자 X 및 에 대해서는 이러한 반례가 발생할 수 없습니다. σ{\ \}} σ psigma _{p}}가 상태ψ {\displaystyle \psi}에서 되는 한, 하이젠베르크 불확정성 원리는 다음과 같습니다. ψ\psi}이(가) XP^ {\hat {P}} P hat{X}}의 에 있지 않은 경우에도 마찬가지입니다.
추가 불확실성 관계
하이젠베르크 한계
양자 계측, 특히 간섭계에서 하이젠베르크 한계는 측정의 정확도가 측정에 사용된 에너지에 따라 확장될 수 있는 최적의 속도입니다. 일반적으로 이것은 위상(빔 분할기의 한쪽 팔에 적용)을 측정하는 것이며 에너지는 간섭계에 사용된 광자 수에 의해 제공됩니다. 일부에서는 하이젠베르크 한계를 깼다고 주장하지만, 이는 스케일링 리소스의 정의에 대한 이견을 반영합니다.[55] 적절하게 정의하면, 하이젠베르크 한계는 양자역학의 기본 원리의 결과이며, 약한 하이젠베르크 한계는 이길 수 있지만, 이길 수 없습니다.[56]
체계적이고 통계적인 오류
위의 부등식은 표준 편차σ\sigma에 의해 정량화된 관측 가능한 것의 통계적 부정확성에 초점을 맞추고 있습니다. 그러나 하이젠베르크의 원래 버전은 시스템 오류, 즉 측정 장치에 의해 생성되는 양자계의 교란, 즉 관측자 효과를 다루고 있었습니다.
εA displaystyle \{A}}가 오류를 나타내도록 하면 (즉, 부정확) 관측 가능한 A 및η B _{B}}의 측정 결과 A의 이전 측정에 의한 공액 변수 B의 후속 측정 시 발생하는 교란, 그리고 오자와가 제안한 체계적 및 통계적 오류를 모두 포함하는 부등식은 다음과 같습니다.
하이젠베르크의 불확정성 원리는 원래 1927년 공식에서 설명한 바와 같이, 체계적 오류와 관련하여 오자와 불평등의 첫 번째 항만 언급합니다. 위의 표기법을 사용하여 순차 측정의 오차/교란 효과를 설명하면 다음과 같습니다(처음에는 A, 다음에는 B).
하이젠베르크 관계의 공식적인 유도는 가능하지만 직관적이지는 않습니다. 하이젠베르크에 의해 제안된 것이 아니라 최근에서야 수학적으로 일관된 방식으로 공식화되었습니다.[57][58] 또한 하이젠베르크 공식이 고유한 통계적 오류를 고려하지 않고 있다는 점을 강조해야 합니다 σ A _{} σ B sigma _{B}. 하이젠베르크 용어만으로는 전체 양자 불확실성을 설명할 수 없다는 실험적 증거가 증가하고 있습니다. 오자와 부등식의 세 항이 모두 존재해야 합니다.
동일한 형식주의를 [1]사용하면 이전과 종종 혼동되는 다른 종류의 물리적 상황, 즉 동시 측정의 경우(A와 B가 동시에)를 소개할 수도 있습니다.
A와 B의 두 가지 동시 측정값은 반드시[62] 날카롭지 않거나 약합니다.
오자와의 관계와 같이 통계적 및 체계적 오류 구성 요소를 모두 결합하지만 하이젠베르크 원래의 부등식에 매우 가까운 형태를 유지하는 불확실성 관계를 도출할 수도 있습니다. 로버트슨을[1] 추가함으로써
오자와의 관계는 우리가 얻는 것입니다.
양자 엔트로피 불확정성 원리
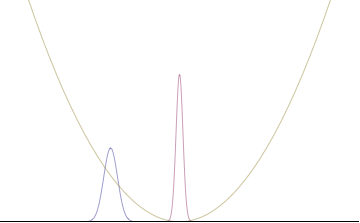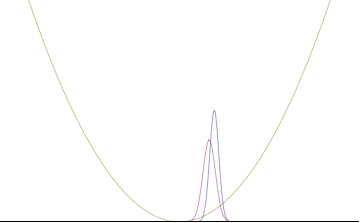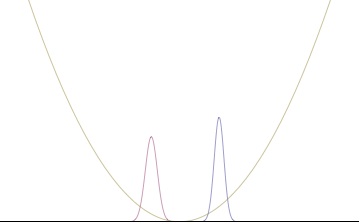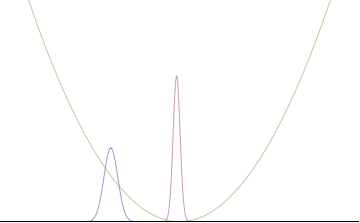
많은 분포의 경우 표준 편차는 구조를 정량화하는 특별한 자연스러운 방법이 아닙니다. 예를 들어, 관측치 중 하나가 각도인 불확실성 관계는 한 주기보다 큰 변동에 대해 물리적 의미가 거의 없습니다.[41][64][65][66] 다른 예로는 고도의 이중 모드 분포 또는 분산이 다른 단일 모드 분포가 있습니다.
이러한 문제를 극복하는 해결책은 분산의 곱 대신 엔트로피 불확실성에 기반한 불확실성입니다. 1957년 휴 에버렛 3세는 양자역학의 다세계 해석을 공식화하면서 엔트로피적 확실성에 기초한 불확정성 원리의 더 강력한 확장을 추측했습니다.[67] I. I. 허쉬만에[68] 의해서도 연구되고 1975년에 W. Beckner에[69] 의해서 그리고 Iwo Bialynicki-Birula와 Jerzy Miccielski에[70] 의해서 증명된 이 추측은 두 정규화된 무차원 푸리에 변환 쌍 f(a)와 g(b)에 대해서 여기서
- and
섀넌 정보 항목
여기서 로그는 임의의 기저에 있을 수 있습니다.
위치 파동 함수 ψ(x) 및 운동량 파동 함수 φ(x)와 관련된 확률 분포 함수들은 각각 역길이 및 운동량의 차원을 갖지만, 엔트로피들은 다음에 의해 무차원으로 렌더링될 수 있음
여기서 그는 플랑크 상수입니다.
xp00 제품의 선택에 따라 여러 가지 방법으로 표현할 수 있습니다. xp가00 bh로 선택되면,
대신 xp를 ħ로 선택하면,
x와0 p가0 사용 중인 단위 시스템에서 통일성을 갖도록 선택되면 다음과 같습니다.
양자 엔트로피 불확정성 원리는 하이젠베르크 불확정성 원리보다 더 제한적입니다. 역로그 소볼레프 부등식으로부터[72]
다시 말해, 하이젠베르크 불확정성 원리는 양자 엔트로피 불확정성 원리의 결과이지만, 그 반대는 아닙니다. 이러한 불평등에 대한 몇 가지 언급. 첫째, base e의 선택은 물리학의 대중적인 관습의 문제입니다. 부등식의 양변에서 일치하는 경우 로그는 임의의 기저에 있을 수 있습니다. 둘째, 양자 폰 노이만 엔트로피가 아니라 샤넌 엔트로피가 사용되었다는 것을 기억하십시오. 마지막으로, 정규 분포는 부등식을 포화시키고, 고정된 분산을 갖는 분포 중 최대 엔트로피 확률 분포이기 때문에 이 속성을 갖는 유일한 분포입니다(cf). 증명을 위해 여기에)
| 정규 분포의 엔트로피 불확실성 |
|---|
| 우리는 위에서 논의한 바와 같이 표준 편차를 기반으로 일반적인 불확실성을 포화시키는 QHO의 지상 상태에서 이 방법을 시연합니다. 길이 척도는 편리한 대로 설정할 수 있으므로 할당합니다. 확률 분포는 정규 분포입니다. 섀넌 엔트로피로 운동량 분포에 대해서는 완전히 유사한 계산이 진행됩니다. =ℏ / x 0 {\{0} =x_{0}}}의 표준 운동량 선택: 따라서 엔트로피 불확실성이 한계값입니다. |
측정 장치는 가능한 출력을 빈으로 이산화하여 설정된 유한 해상도를 가지며, Born 규칙에 의해 주어진 빈 중 하나 내에 놓일 확률이 있습니다. 우리는 통의 크기가 균일한 가장 일반적인 실험 상황을 고려할 것입니다. δ x를 공간 해상도의 척도라고 합니다. 우리는 0번째 빈이 원점 근처에 중심을 두고 있으며, 약간의 일정한 오프셋 c가 있을 수 있습니다. 폭 δ x의 j번째 구간 내에 놓일 확률은 다음과 같습니다.
이러한 이산화를 설명하기 위해, 우리는 주어진 측정 장치에 대한 파동 함수의 섀넌 엔트로피를 다음과 같이 정의할 수 있습니다.
위 정의에서 엔트로피 불확정성 관계는
여기서 우리는 δ x δ p/h가 분할 함수의 계산에 사용되는 전형적인 무한소 위상 공간 부피라는 것에 주목합니다. 불평등도 엄격하고 포화 상태가 아닙니다. 이러한 한계를 개선하기 위한 노력은 활발한 연구 분야입니다.
| 정규 분포 예제 |
|---|
| 우리는 위에서 논의한 바와 같이 표준 편차를 기반으로 일반적인 불확실성을 포화시키는 QHO의 지상 상태에서 이 방법을 먼저 시연합니다. 이 빈들 중 하나 내에 누워 있을 확률은 오차 함수로 표현할 수 있습니다. 운동량 확률은 완전히 유사합니다. 단순화를 위해 해상도를 다음과 같이 설정합니다. 그래서 확률이 다음으로 줄어들게 됩니다. 섀넌 엔트로피는 수치적으로 평가할 수 있습니다. 엔트로피 불확실성은 실제로 한계값보다 큽니다. 최적의 경우임에도 불구하고 부등식이 포화되지 않았습니다. |
| Sinc 함수 예제 |
|---|
| 분산이 무한한 단모달 분포의 예로는 sinc 함수가 있습니다. 파동함수가 정확하게 정규화된 균일분포이면 그러면 푸리에 변환은 sinc 함수이고, 중앙에 집중된 모양을 가지고 있음에도 불구하고 무한한 운동량 분산을 생성합니다. 반면 엔트로피 불확실성은 유한합니다. 단순화를 위해 공간 해상도가 단지 2-빈 측정, δ x = a, 운동량 해상도가 δ p = h/a라고 가정합니다. 균일한 공간 분포를 두 개의 동일한 빈으로 분할하는 것은 간단합니다. 두 통이 분포에 걸쳐 있도록 오프셋 c = 1/2을 설정했습니다. 운동량을 위한 통은 전체 실선을 덮어야 합니다. 공간 분포와 마찬가지로 오프셋을 적용할 수 있습니다. 그러나 운동량에 대한 0번째 빈이 원점에 중심을 둘 때 섀넌 엔트로피가 최소화되는 것으로 밝혀졌습니다. ( 독자는 오프셋을 추가해 볼 것을 권장합니다.) 임의의 운동량 빈 내에 놓일 확률은 사인 적분으로 표현할 수 있습니다. 섀넌 엔트로피는 수치적으로 평가할 수 있습니다. 엔트로피 불확실성은 실제로 한계값보다 큽니다. |
3개의 각운동량 성분과의 불확정성 관계
j의 입자에 대해 다음과 같은 불확정성 관계가 성립합니다.
고조파 분석
수학의 한 분야인 고조파 분석의 맥락에서 불확정성 원리는 함수의 값과 푸리에 변환을 동시에 위치시킬 수 없음을 의미합니다. 참고로, 다음과 같은 부등식이 성립합니다.
위의 엔트로피 불확실성을 포함한 추가적인 수학적 불확실성 부등식은 함수 f와 푸리에 변환 ƒ̂ 사이에 있습니다.
신호처리
신호 처리, 특히 시간-주파수 분석의 맥락에서 불확실성 원리는 Dennis Gabor 다음으로 Gabor 한계 또는 때때로 Heisenberg-Gabor 한계로 언급됩니다. 아래의 "베네딕스 정리"에서 나온 기본적인 결과는 함수가 시간 제한과 대역 제한 둘 다를 가질 수 없다는 것입니다(함수와 푸리에 변환 둘 다 경계 영역을 가질 수 없음). 대역 제한과 시간 제한을 참조하십시오. 보다 정확하게 시간 대역폭 또는 지속 시간 대역폭 제품은 다음을 만족합니다.
또는 "한 사람은 시간 영역과 주파수 영역(ƒ̂, 그 푸리에 변환) 모두에서 신호(함수 f)를 동시에 급격하게 위치시킬 수 없습니다."라고 말합니다.
필터에 적용하면 결과는 높은 시간 해상도와 주파수 해상도를 동시에 달성할 수 없음을 의미합니다. 구체적인 예는 짧은 시간 푸리에 변환의 해상도 문제입니다. 넓은 창을 사용하면 시간 해상도 비용으로 좋은 주파수 해상도를 달성할 수 있습니다. 좁은 창은 반대의 트레이드오프를 가지고 있습니다.
대체 정리는 보다 정확한 정량적 결과를 제공하며, 시간-주파수 분석에서는 (1차원) 시간 및 주파수 영역을 별도로 해석하는 대신 (2차원) 시간-주파수 평면에서 함수를 지원하는 하한으로 해석합니다. 실제로 가보르 한계는 간섭 없이 달성할 수 있는 동시 시간-주파수 분해능을 제한합니다. 더 높은 분해능을 달성하는 것이 가능하지만 신호의 다른 구성 요소가 서로 간섭하는 비용을 지불합니다.
따라서 과도현상이 중요한 신호를 분석하기 위해 푸리에 대신 웨이블릿 변환을 사용하는 경우가 많습니다.
이산 푸리에 변환
x = 0 - N-1}는N개의 복소수 시퀀스이고 {XX , ,X -,X_{X_{ 이산 푸리에 변환#불확실성 원리.
Denote by the number of non-zero elements in the time sequence and by the number of non-zero elements in the frequency sequence N- 그리고나서,
이 부등식은 급격하며, x 또는 X가 디랙 질량일 때, 또는 x가 정수 모듈론 N의 부분군에서 지원되는 디랙 빗의 0이 아닌 배수일 때, 또는 더 일반적으로 x가 정수 모듈론 N의 부분군에서 지원되는 디랙 빗의 0이 아닌 배수일 때 달성됩니다(이 경우 X도 보완 부분군에서 지원되는 디랙 빗이며, 그 반대도 마찬가지입니다).
일반적으로 T와 W가 정수 모듈론 N의 부분 집합이라면 :ℓ ( N Z) →ℓ 2 (Z / N Z) L_ R_{W}:\ / N \ / N\mathbb {Z})}는 각각 시간 limiting 연산자와 대역 limiting 연산자를 나타냅니다. 그리고나서
N이 소수일 때 더 강한 부등식은 다음과 같습니다.
베네딕스 정리
암라인-베르티에와 베네딕스의 정리는 f가 0이 아닌 점들의 집합과 ƒ̂가 0이 아닌 점들의 집합이 모두 작을 수 없다는 것을 직관적으로 말해줍니다.
특히, 유한 르베그 측정 집합에서 L(R)에서의 함수 f와 푸리에 변환 ƒ̂이 모두 지원되는 것은 불가능합니다. 좀 더 정량적인 버전은[82][83]
요인 Ce가 S 또는 σ 중 하나가 볼록인 경우에만 알 수 있는 Ce로 대체될 수 있다고 예상합니다.
하디의 불확정성 원리
수학자 G. H. 하디는 다음과 같은 불확정성 원리를 공식화했습니다: f와 ƒ̂ 모두 "매우 빠르게 감소"하는 것은 불가능합니다. 구체적으로, ( 의 f가 다음과 같은 경우
이는 나중에 다음과 같이 개선되었습니다. ∈ ) in L^{{R} ^{d})가 다음과 같습니다.
이 결과는 베얼링의 전집에 증명 없이 진술되었고, 일반적인 경우에 대해서는 회르만데르(경우 = = d=N=와 보나미, 데망주, 자밍에서 증명되었습니다. Hörmander-Beurling의 버전은 하디 정리의 경우 ab > 1을 의미하며, Bonami-Demange-Jaming의 버전은 하디 정리의 전체 강도를 다룹니다. 리우빌 정리에 기초한 베얼링 정리의 다른 증명이 참고문헌에 등장했습니다.[87]
사례 ab < 1에 대한 전체 설명과 Schwartz 클래스 분포에 대한 다음 확장이 참조에 나타납니다.[88]
정리 — 강화 분포 ∈ ( f\ {R} ^{d})가 다음과 같은 경우
역사
1925년 하이젠베르크는 행렬역학으로 알려진 최초의 양자역학 이론을 발표했습니다. 맥스 본과 파스쿠알 조던과 함께 작업하면서, 그는 점점 더 성공적인 이론을 계속 발전시켰습니다.[89] 이 이론의 중심적인 측면은 비가환성이었습니다: 이론은 위치와 운동량 측정의 상대적인 순서가 중요하다는 것을 암시했습니다.

1926년 3월, 보어의 연구소에서 일하면서 하이젠베르크는 비가환성이 불확정성 원리를 내포한다는 것을 깨달았습니다. 1927년 2월 볼프강 파울리에게 편지를 쓰면서, 그는 기본적인 개념들을 생각해 냈습니다.[90]
하이젠베르크는 1927년에 발표한 저명한 논문 "Uber den anschaulichen Inhalt der quantoretischen Kinematik und Mechanik"에서 이 표현식을 위치 측정에 의해 발생하는 피할 수 없는 운동량 교란의 최소량으로 정의했습니다.[2] 하지만 δ엑스와 δ프의 불확실성에 대해서는 정확한 정의를 내리지 않았습니다. 대신 각 경우에 따라 몇 가지 그럴듯한 추정치를 개별적으로 제공했습니다. 그의 논문은 보어가 부정확하다는 것을 보여주는 현미경의 관점에서 분석을 제공했습니다. 하이젠베르크는 이 논문에 부록을 포함시켰습니다.
1930년 시카고 강연에서[91] 그는 자신의 원칙을 다듬었습니다.
-
(A1)
이후의 작업은 개념을 넓혔습니다. 통근하지 않는 두 변수는 동시에 측정할 수 없습니다. 한 변수를 더 정확하게 알수록 다른 변수를 더 정확하게 알 수 있습니다. 하이젠베르크는 다음과 같이 썼습니다.
다음과 같이 가장 간단한 형태로 표현할 수 있습니다. 가장 작은 입자 중 하나의 움직임을 결정하는 두 가지 중요한 요소, 즉 입자의 위치와 속도를 완벽하게 정확하게 알 수는 없습니다. 입자의 위치와 방향과 속도를 동시에 정확히 파악하는 것은 불가능합니다.[92]
1927년 케너드는[6][1]: 204 현대의 부등식을 처음으로 증명했습니다.
-
(A2)
ħ = h/2 π 및 σ에서 σ는 위치 및 운동량의 표준 편차입니다. (하이젠베르크는 가우스 상태의 특수한 경우에만 관계 (A2)를 증명했습니다.)[91] 1929년 로버트슨은 부등식을 모든 관측 가능한 것으로 일반화했고 1930년 슈뢰딩거는 연산자의 공분산이 0이 아닌 것을 허용하도록 형태를 확장했습니다.[1]: 204
용어 및 번역
하이젠베르크는 독일어로 쓰여진 그의 원래 1927년 논문의 본문 전체에 걸쳐 기본적인 이론적 원리를 설명하기 위해 [2]"Ungenauigkeit"이라는 단어를 사용했습니다. 마지막 메모에서 그는 "Unsicherheit"라는 단어로 전환했습니다. 나중에 그는 항상 "Unbestimmit"을 사용했습니다. 그러나 1930년 하이젠베르크의 교과서인 '양자론의 물리적 원리'의 영문판이 출간되었을 때, '불확실성'이라는 영어 단어만 사용되었고, 영어에서는 '불확실성'이라는 용어가 되었습니다.[93]
하이젠베르크 현미경

그 원리는 꽤 반직관적이기 때문에 양자 이론의 초기 학생들은 그것을 위반하기 위한 순진한 측정은 항상 실행 불가능할 수밖에 없다는 것을 확신해야 했습니다. 하이젠베르크가 원래 불확정성 원리를 위반하는 본질적인 불가능성을 설명한 한 가지 방법은 가상 현미경의 관찰자 효과를 측정 장치로 사용하는 것입니다.[91]
그는 광자를 쏘아 전자의 위치와 운동량을 측정하려는 실험자를 상상합니다.[94]: 49–50
- 문제 1 – 광자가 파장이 짧고, 따라서 운동량이 크면 위치를 정확하게 측정할 수 있습니다. 그러나 광자는 무작위 방향으로 산란하여 크고 불확실한 양의 운동량을 전자로 전달합니다. 광자가 파장이 길고 운동량이 적으면 충돌이 전자의 운동량을 크게 방해하지는 않지만 산란은 위치를 애매하게 드러낼 뿐입니다.
- 문제 2 – 현미경에 큰 조리개를 사용하면 전자의 위치를 잘 해결할 수 있지만(Rayleigh 기준 참조) 운동량 보존 원리에 의해 들어오는 광자의 가로 운동량이 전자의 빔라인 운동량에 영향을 미치므로 전자의 새로운 운동량은 잘 해결되지 않습니다. 작은 조리개를 사용하면 두 해상도의 정확도가 그 반대입니다.
이러한 트레이드오프의 조합은 어떤 광자 파장과 조리개 크기를 사용하든 측정된 위치와 측정된 운동량의 불확실성의 곱이 플랑크 상수와 동일한 하한 값 이상임을 의미합니다.[95] 하이젠베르크는 불확정성 원리를 정확한 극한으로 공식화하는 데 신경 쓰지 않았고, 대신 휴리스틱 정량적 진술로 작은 수치 요소까지 수정하는 것을 선호했는데, 이는 양자 역학의 근본적으로 새로운 비상호성을 불가피하게 만듭니다.
비판적 반응
사실 양자역학에 대한 코펜하겐의 해석과 하이젠베르크의 불확정성 원리는 처음에는 반대론자들에 의해 쌍둥이 목표물로 여겨졌습니다. 양자역학의 코펜하겐 해석에 따르면, 양자 상태가 설명하는 근본적인 실체는 없으며, 단지 실험 결과를 계산하기 위한 처방일 뿐입니다. 시스템의 상태가 근본적으로 무엇인지 말할 수 있는 방법은 없으며, 단지 관찰의 결과가 무엇일지만 알 수 있습니다.
알버트 아인슈타인은 무작위성이 현실의 어떤 근본적인 속성에 대한 우리의 무지의 반영이라고 믿었고, 닐스 보어는 확률 분포가 근본적이고 줄일 수 없으며 우리가 어떤 측정을 수행하기로 결정하는지에 따라 달라진다고 믿었습니다. 아인슈타인과 보어는 불확정성 원리에 대해 여러 해 동안 논쟁을 벌였습니다.
이상적인 분리 관측자
볼프강 파울리는 불확정성 원리에 대한 아인슈타인의 근본적인 반대를 "분리된 관찰자의 이상"이라고 불렀습니다.
"달이 확실한 위치를 가지고 있는 것처럼" 지난 겨울 아인슈타인은 저에게 "우리가 달을 보든 보지 않든, 이것들과 거시적인 물체들 사이에 가능한 뚜렷한 구별이 없기 때문에 원자 물체들에게도 동일한 위치가 유지되어야 합니다. 관찰은 위치와 같은 현실의 요소를 만들 수 없으며, 물리적 현실의 완전한 묘사에 포함된 것이 있어야 하며, 이는 관찰이 실제로 이루어지기 전에 이미 위치를 관찰할 수 있는 가능성에 해당합니다." 저는 제가 아인슈타인을 정확하게 인용했기를 바랍니다. 누군가가 동의하지 않는 사람을 기억에서 인용하는 것은 항상 어렵습니다. 내가 분리된 관찰자의 이상이라고 부르는 것은 바로 이런 종류의 공준입니다.
— Letter from Pauli to Niels Bohr, February 15, 1955[96]
아인슈타인의 슬릿
불확정성 원리에 도전한 아인슈타인의 첫 번째 사고 실험은 다음과 같이 진행되었습니다.
폭 d의 슬릿을 통과하는 입자를 생각해 보자. 슬릿은 입자가 벽을 통과하기 때문에 대략 h/d의 운동량 불확실성을 발생시킵니다. 하지만 벽의 반동을 측정하여 입자의 운동량을 결정합니다. 이를 통해 운동량 보존을 통해 입자의 운동량을 임의의 정확도로 찾습니다.
보어의 반응은 벽이 양자역학적이기도 하고, 반동을 정확도 δp로 측정하기 위해서는 입자가 통과하기 전에 벽의 운동량을 이 정도로 알아야 한다는 것이었습니다. 이는 벽의 위치 및 따라서 h/δp와 동일한 슬릿의 위치에 불확실성을 초래하며, 벽의 운동량이 반동을 측정할 수 있을 정도로 정확하게 알려져 있다면 슬릿의 위치는 위치 측정을 허용하지 않을 정도로 불확실합니다.
Richard Feynman은 입자가 여러 개의 슬릿을 통해 회절하는 유사한 분석을 제공합니다.[97]
아인슈타인 상자
보어는 아인슈타인이 아인슈타인의 상자로 알려진 사고 실험을 제안했을 때 참석했습니다. 아인슈타인은 "하이젠베르크의 불확정성 방정식은 시간의 불확정성이 에너지의 불확정성과 관련이 있다는 것을 암시했고, 둘의 곱은 플랑크 상수와 관련이 있습니다."라고 주장했습니다.[98] 그는 이상적인 상자라고 생각해보세요. 거울이 줄지어 있어서 빛을 무한정 담을 수 있습니다. 시계 장치가 하나의 단일 광자가 빠져나갈 수 있도록 선택된 순간에 이상적인 셔터를 열기 전에 상자의 무게를 측정할 수 있습니다. "우리는 이제 광자가 상자를 떠난 시간을 알고 있습니다."[99] "자, 상자의 무게를 다시 잰다. 질량의 변화는 방출된 빛의 에너지를 말해줍니다. 이런 식으로, 아인슈타인은 불확실성 원리에 반하는 어떤 원하는 정밀도로 방출되는 에너지와 방출되는 시간을 측정할 수 있다고 말했습니다."[98]
보어는 이 논쟁을 생각하며 잠 못 이루는 밤을 보냈고, 결국 그것이 결함이 있다는 것을 깨달았습니다. 그는 만약 무게를 측정하려면, 예를 들어 스프링과 눈금의 포인터로 무게를 측정해야 하기 때문에 수직 속도에 불확실성이 있을 것이며, 따라서 테이블 위 높이에 불확실성이 있을 것이라고 지적했습니다. 게다가, 아인슈타인 자신의 중력 이론이 시간에 미치는 영향 때문에 지구 표면의 고도에 대한 불확실성은 시계 속도에 불확실성을 초래할 것입니다."[100] "이러한 불확실성의 연쇄를 통해 보어는 아인슈타인의 라이트 박스 실험이 광자의 에너지와 탈출 시간을 동시에 정확하게 측정할 수 없다는 것을 보여주었습니다."[101]
얽힌 입자에 대한 EPR 역설
1935년 아인슈타인, 보리스 포돌스키, 네이선 로젠은 공간적으로 분리된 얽힌 입자(EPR 역설)에 대한 분석을 발표했습니다.[102] EPR에 따르면 얽힌 입자 중 하나의 위치와 두 번째 입자의 운동량을 측정할 수 있으며, 이러한 측정을 통해 두 입자의 위치와 운동량을 임의의 정밀도로 추론하여 불확실성 원칙에 위배됩니다. 그러한 가능성을 피하기 위해서는 한 입자의 측정이 다른 입자의 확률 분포를 순간적으로 수정해야 하며, 이는 국소성의 원칙에 위배될 수 있습니다.[103]
1964년 존 스튜어트 벨(John Stewart Bell)은 이 가정이 서로 다른 실험의 확률 사이에 일정한 불평등을 의미하기 때문에 위조될 수 있음을 보여주었습니다. 실험 결과는 국소 숨은 변수의 EPR 기본 가정을 배제하고 양자 역학의 예측을 확인합니다.
포퍼의 비평
과학철학자 칼 포퍼는 불확정성의 문제를 논리학자이자 형이상학적 실재론자로서 접근했습니다.[104] 그는 불확정성 관계를 동일하게 준비된 입자의 앙상블이 아닌 개별 입자에 적용하는 것에 동의하지 않았으며, 이를 "통계적 산란 관계"라고 불렀습니다.[104][105] 이 통계적 해석에서는 양자 이론을 무효화하지 않고 임의의 정밀도로 특정 측정이 이루어질 수 있습니다.
1934년, 포퍼는 나투르비센샤프텐에 불확정성 관계에 대한 비판(Zur Kritik der Ungenauigkeits relationen)을 발표하고,[106] 같은 해 Logik der Forschung(1959년 저자에 의해 과학적 발견의 논리로 번역되고 업데이트됨)을 발표하여 통계적 해석에 대한 자신의 주장을 설명했습니다. 1982년에 그는 양자론과 물리학의 분열에 관한 자신의 이론을 더욱 발전시켰습니다.
[하이젠베르크] 공식은 의심의 여지 없이 양자 이론의 유도 가능한 통계 공식입니다. 그러나 이러한 공식이 측정의 정확성에 대한 어떤 상한을 결정하는 것으로 해석될 수 있다고 말한 양자 이론가들에 의해 습관적으로 잘못 해석되었습니다. [원래 강조점][107]
포퍼는 불확실성 관계를 위조하는 실험을 제안했지만, 나중에 칼 프리드리히 폰 바이제커, 하이젠베르크, 아인슈타인과 논의한 후 초기 버전을 철회했습니다. 이 실험은 EPR 역설의 공식화에 영향을 미쳤습니다.[104][108]
자유의지
아서 콤프턴과[109] 마틴 하이젠베르크를[110] 포함한 일부 과학자들은 불확정성 원리, 또는 적어도 양자역학의 일반적인 확률론적 특성이 자유의지의 2단계 모델에 대한 증거가 될 수 있다고 제안했습니다. 그러나 한 가지 비판은 화학의 기초로서 양자역학의 기본적인 역할 외에도 실온에서 양자 시스템의 빠른 디코히어런스 시간으로 인해 양자역학이 필요한 사소한 생물학적 메커니즘은 가능성이 낮다는 것입니다.[111] 이 이론의 지지자들은 일반적으로 이러한 디코히어런스가 생물학적 세포에서 발견되는 스크리닝과 디코히어런스가 없는 하위 공간 모두에 의해 극복된다고 말합니다.[111]
열역학
불확정성 원리를 위반하는 것도 열역학 제2법칙 위반을 강하게 내포한다고 볼 만한 이유가 있습니다.[112] 깁스 역설 참조.
원칙거부
불확정성 원리는 양자 입자-전자-예를 들어 고전적인 개념-위치 및 운동량과 관련이 있습니다. 이는 양자 입자가 위치와 운동량을 가진다고 가정합니다. 에드윈 C. 1937년 켐블은 그러한 성질들이 실험적으로 검증될 수 없으며, 그것들이 존재한다고 가정하면 많은 모순이 생긴다고 지적했습니다[113]. 마찬가지로 루돌프 하그는 양자역학에서의 위치는 전자와 검출기 사이의 상호작용의 속성이지 본질적인 속성이 아니라고 지적했습니다.[114][115] 이러한 관점에서 불확정성 원리는 근본적인 양자적 성질이 아니라 켐블이 말한 것처럼 "조상들의 언어로부터 계승된" 개념입니다.
적용들
불확정성 원리는 양자역학에서 매우 기본적인 결과이기 때문에 양자역학의 전형적인 실험은 일상적으로 그 측면을 관찰합니다. 입자 물리학을 포함한 모든 형태의 분광학은 측정된 에너지 선폭을 양자 상태의 수명과 연관시키기 위해 관계를 사용합니다. 그러나 특정 실험은 주요 연구 프로그램의 일부로 특정 형태의 불확실성 원리를 의도적으로 테스트할 수 있습니다. 여기에는 예를 들어 초전도[116] 또는 양자 광학[117] 시스템에서 수-위상 불확실성 관계의 테스트가 포함됩니다. 작동에 대한 불확실성 원리에 의존하는 애플리케이션에는 중력파 간섭계에 필요한 것과 같은 극도로 낮은 노이즈 기술이 포함됩니다.[118]
참고 항목
- 대응원리
- 양자역학개론
- 쾨프뮐러의 불확정성 원리
- 양자 불확정성
- 양자 터널링
- 물리학과 그 너머 (하이젠베르크의 회고)
- 더 강력한 불확실성 관계
참고문헌
- ^ a b c d e f g h i Sen, D. (2014). "The Uncertainty relations in quantum mechanics" (PDF). Current Science. 107 (2): 203–218. Archived (PDF) from the original on 2019-09-24. Retrieved 2016-02-14.
- ^ a b c Heisenberg, W. (1927) [1927-03-01]. "Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik". Zeitschrift für Physik (in German). 43 (3): 172–198. Bibcode:1927ZPhy...43..172H. doi:10.1007/BF01397280. ISSN 0044-3328. S2CID 122763326.Heisenberg, W (1983) [1927]. "The actual content of quantum theoretical kinematics and mechanics". No. NAS 1.15: 77379. 1983. 43 (3–4): 172. Bibcode:1983ZhPhy..43..172H. Archived from the original on 2023-09-02. Retrieved 2023-08-28.
English translation of Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik
- ^ 베르너 하이젠베르크(1989), 아인슈타인과의 만남과 사람, 장소와 입자에 관한 다른 에세이, 프린스턴 대학 출판부, 53쪽.[ISBN missing]
- ^ Dolling, Lisa M.; Gianelli, Arthur F.; Statile, Glenn N., eds. (2003). The Tests of Time. doi:10.1515/9781400889167. ISBN 978-1400889167.
- ^ 쿠마르, 만짓. 양자: 아인슈타인, 보어, 그리고 현실의 본질에 대한 위대한 논쟁. 2008년 제1회 미국판. 10장, 주 37.[ISBN missing]
- ^ a b c Kennard, E. H. (1927), "Zur Quantenmechanik einfacher Bewegungstypen", Zeitschrift für Physik (in German), 44 (4–5): 326–352, Bibcode:1927ZPhy...44..326K, doi:10.1007/BF01391200, S2CID 121626384.
- ^ Weyl, H. (1928). Gruppentheorie und Quantenmechanik (in German). Leipzig: Hirzel.[페이지 필요]
- ^ Jaeger, Gregg (September 2014). "What in the (quantum) world is macroscopic?". American Journal of Physics. 82 (9): 896–905. Bibcode:2014AmJPh..82..896J. doi:10.1119/1.4878358.
- ^ 부록 B 참조
- ^ Claude Cohen-Tannoudji; Bernard Diu; Franck Laloë (1996), Quantum mechanics, Wiley-Interscience: Wiley, pp. 231–233, ISBN 978-0-471-56952-7
- ^ a b c Landau, Lev Davidovich; Lifshitz, Evgeny Mikhailovich (1977). Quantum Mechanics: Non-Relativistic Theory. Vol. 3 (3rd ed.). Pergamon Press. ISBN 978-0-08-020940-1.
- ^ a b c d e f Busch, Paul (2002). "The Time-Energy Uncertainty Relation". In Muga, J. G.; Mayato, R. Sala; Egusquiza, I. L. (eds.). Time in Quantum Mechanics. Lecture Notes in Physics. Vol. 72. Berlin, Heidelberg: Springer Berlin Heidelberg. pp. 69–98. doi:10.1007/3-540-45846-8_3. ISBN 978-3-540-43294-4.
- ^ Wigner, E. P. (1997). "On the Time–Energy Uncertainty Relation". In Wightman, Arthur S. (ed.). Part I: Particles and Fields. Part II: Foundations of Quantum Mechanics. Berlin, Heidelberg: Springer Berlin Heidelberg. pp. 538–548. doi:10.1007/978-3-662-09203-3_58. ISBN 978-3-642-08179-8.
- ^ a b Hilgevoord, Jan (1996-12-01). "The uncertainty principle for energy and time". American Journal of Physics. 64 (12): 1451–1456. Bibcode:1996AmJPh..64.1451H. doi:10.1119/1.18410. ISSN 0002-9505. Archived from the original on 2024-02-23. Retrieved 2023-11-12.
- ^ Lynch, F. J.; Holland, R. E.; Hamermesh, M. (1960-10-15). "Time Dependence of Resonantly Filtered Gamma Rays from Fe 57". Physical Review. 120 (2): 513–520. doi:10.1103/PhysRev.120.513. ISSN 0031-899X.
- ^ Frauenfelder, H. (1962). The Mössbauer Effect. W. A. Benjamin. p. 66. LCCN 61018181.
- ^ Bohm, Arno R.; Sato, Yoshihiro (2005-04-28). "Relativistic resonances: Their masses, widths, lifetimes, superposition, and causal evolution". Physical Review D. 71 (8): 085018. arXiv:hep-ph/0412106. Bibcode:2005PhRvD..71h5018B. doi:10.1103/PhysRevD.71.085018. ISSN 1550-7998. S2CID 119417992.
- ^ 카플러스, 마틴, 포터, 리처드 니덤(1970). 원자와 분자. 캘리포니아: Benjamin Cummings. p. 68 ISBN 978-0805352184. OCLC 984466711
- ^ 빠르게 붕괴하는 상태의 선폭이 넓어 상태의 에너지를 정확하게 측정하기가 어렵고, 연구자들은 더 날카로운 피크를 얻기 위해 붕괴 속도를 늦추기 위해 디튜닝된 마이크로파 캐비티를 사용하기도 했습니다.
- ^ a b Hilgevoord, Jan (March 2005). "Time in quantum mechanics: a story of confusion". Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics. 36 (1): 29–60. Bibcode:2005SHPMP..36...29H. doi:10.1016/j.shpsb.2004.10.002. Archived from the original on 2022-10-23. Retrieved 2024-01-28.
- ^ Bohm, Arno (January 2011). "Resonances/decaying states and the mathematics of quantum physics". Reports on Mathematical Physics. 67 (3): 279–303. Bibcode:2011RpMP...67..279B. doi:10.1016/S0034-4877(11)60018-9. Archived from the original on 2023-12-04. Retrieved 2024-01-24.
- ^ Aharonov, Y.; Bohm, D. (June 1, 1961). "Time in the Quantum Theory and the Uncertainty Relation for Time and Energy" (PDF). Physical Review. 122 (5): 1649–1658. Bibcode:1961PhRv..122.1649A. doi:10.1103/PhysRev.122.1649. Archived from the original (PDF) on 2014-01-09. Retrieved 2012-01-21.
- ^ L. I. 만델스탐, I. E. 탐, 비상대론적 양자역학에서 에너지와 시간의 불확실성 관계 1945년 Wayback Machine에서 아카이브된 2019-06-07.
- ^ Naber, Gregory L. (2021). Quantum Mechanics: An Introduction to the Physical Background and Mathematical Structure. Walter de Gruyter GmbH & Co KG. p. 230. ISBN 978-3-11-075194-9. Archived from the original on 2024-02-23. Retrieved 2024-01-20.
- ^ a b c d e Griffiths, David J.; Schroeter, Darrell F. (2018). Introduction to Quantum Mechanics (3rd ed.). Cambridge University Press. Bibcode:2018iqm..book.....G. doi:10.1017/9781316995433. ISBN 978-1-316-99543-3. Archived from the original on 2024-02-23. Retrieved 2024-01-27.
- ^ Furuta, Aya (2012), "One Thing Is Certain: Heisenberg's Uncertainty Principle Is Not Dead", Scientific American, archived from the original on 2022-04-01, retrieved 2018-10-20
- ^ a b Ozawa, Masanao (2003), "Universally valid reformulation of the Heisenberg uncertainty principle on noise and disturbance in measurement", Physical Review A, 67 (4): 42105, arXiv:quant-ph/0207121, Bibcode:2003PhRvA..67d2105O, doi:10.1103/PhysRevA.67.042105, S2CID 42012188
- ^ Wheeler, John Archibald (1978-01-01), Marlow, A. R. (ed.), "The 'Past' and the 'Delayed-Choice' Double-Slit Experiment", Mathematical Foundations of Quantum Theory, Academic Press, pp. 9–48, doi:10.1016/b978-0-12-473250-6.50006-6, ISBN 978-0-12-473250-6, archived from the original on 2022-12-10, retrieved 2023-07-19
- ^ Wheeler, John Archibald (1977), Lopes, José Leite; Paty, Michel (eds.), "Include the Observer in the Wave Function?", Quantum Mechanics, A Half Century Later: Papers of a Colloquium on Fifty Years of Quantum Mechanics, Held at the University Louis Pasteur, Strasbourg, May 2–4, 1974, Episteme, Dordrecht: Springer Netherlands, pp. 1–18, doi:10.1007/978-94-010-1196-9_1, ISBN 978-94-010-1196-9, archived from the original on 2024-02-23, retrieved 2023-07-19
- ^ 베르너 하이젠베르크, 양자 이론의 물리적 원리, p. 20
- ^ a b Rozema, L. A.; Darabi, A.; Mahler, D. H.; Hayat, A.; Soudagar, Y.; Steinberg, A. M. (2012). "Violation of Heisenberg's Measurement–Disturbance Relationship by Weak Measurements". Physical Review Letters. 109 (10): 100404. arXiv:1208.0034v2. Bibcode:2012PhRvL.109j0404R. doi:10.1103/PhysRevLett.109.100404. PMID 23005268. S2CID 37576344.
- ^ De Broglie, Louis (October 1923). "Waves and Quanta". Nature. 112 (2815): 540. Bibcode:1923Natur.112..540D. doi:10.1038/112540a0. ISSN 1476-4687. S2CID 186242764.
- ^ 인도 공과대학 마드라스(Madras), V. 발라크리쉬난(V. Balakrishnan) 교수 강의 1 – 양자물리학 개론 하이젠베르크의 불확정성 원리, 국가기술프로그램의 유튜브 강화 학습
- ^ a b Robertson, H. P. (1929), "The Uncertainty Principle", Phys. Rev., 34 (1): 163–164, Bibcode:1929PhRv...34..163R, doi:10.1103/PhysRev.34.163
- ^ 슈뢰딩거, E., Zum Heisenbergschen Unschärfprinzip, Berliner Berichte, 1930, 페이지 296–303.
- ^ a b Schrödinger, E. (1930), "Zum Heisenbergschen Unschärfeprinzip", Sitzungsberichte der Preussischen Akademie der Wissenschaften, Physikalisch-mathematische Klasse, 14: 296–303
- ^ Riley, K. F.; M. P. Hobson and S. J. Bence (2006), Mathematical Methods for Physics and Engineering, Cambridge, p. 246[ISBN 실종]
- ^ Davidson, E. R. (1965), "On Derivations of the Uncertainty Principle", J. Chem. Phys., 42 (4): 1461–1462, Bibcode:1965JChPh..42.1461D, doi:10.1063/1.1696139
- ^ a b c Hall, B. C. (2013), Quantum Theory for Mathematicians, Springer, p. 245, Bibcode:2013qtm..book.....H
- ^ Jackiw, Roman (1968), "Minimum Uncertainty Product, Number-Phase Uncertainty Product, and Coherent States", J. Math. Phys., 9 (3): 339–346, Bibcode:1968JMP.....9..339J, doi:10.1063/1.1664585
- ^ a b Carruthers, P.; Nieto, M. M. (1968), "Phase and Angle Variables in Quantum Mechanics", Rev. Mod. Phys., 40 (2): 411–440, Bibcode:1968RvMP...40..411C, doi:10.1103/RevModPhys.40.411
- ^ Hall, B. C. (2013), Quantum Theory for Mathematicians, Springer, Bibcode:2013qtm..book.....H
- ^ Maccone, Lorenzo; Pati, Arun K. (31 December 2014). "Stronger Uncertainty Relations for All Incompatible Observables". Physical Review Letters. 113 (26): 260401. arXiv:1407.0338. Bibcode:2014PhRvL.113z0401M. doi:10.1103/PhysRevLett.113.260401. PMID 25615288. S2CID 21334130.
- ^ Huang, Yichen (10 August 2012). "Variance-based uncertainty relations". Physical Review A. 86 (2): 024101. arXiv:1012.3105. Bibcode:2012PhRvA..86b4101H. doi:10.1103/PhysRevA.86.024101. S2CID 118507388.
- ^ a b c d Tóth, Géza; Fröwis, Florian (31 January 2022). "Uncertainty relations with the variance and the quantum Fisher information based on convex decompositions of density matrices". Physical Review Research. 4 (1): 013075. arXiv:2109.06893. Bibcode:2022PhRvR...4a3075T. doi:10.1103/PhysRevResearch.4.013075. S2CID 237513549.
- ^ Tóth, Géza; Petz, Dénes (20 March 2013). "Extremal properties of the variance and the quantum Fisher information". Physical Review A. 87 (3): 032324. arXiv:1109.2831. Bibcode:2013PhRvA..87c2324T. doi:10.1103/PhysRevA.87.032324. S2CID 55088553.
- ^ Yu, Sixia (2013). "Quantum Fisher Information as the Convex Roof of Variance". arXiv:1302.5311 [quant-ph].
- ^ Fröwis, Florian; Schmied, Roman; Gisin, Nicolas (2 July 2015). "Tighter quantum uncertainty relations following from a general probabilistic bound". Physical Review A. 92 (1): 012102. arXiv:1409.4440. Bibcode:2015PhRvA..92a2102F. doi:10.1103/PhysRevA.92.012102. S2CID 58912643.
- ^ Curtright, T.; Zachos, C. (2001). "Negative Probability and Uncertainty Relations". Modern Physics Letters A. 16 (37): 2381–2385. arXiv:hep-th/0105226. Bibcode:2001MPLA...16.2381C. doi:10.1142/S021773230100576X. S2CID 119669313.
- ^ Likharev, K. K.; A. B. Zorin (1985), "Theory of Bloch-Wave Oscillations in Small Josephson Junctions", J. Low Temp. Phys., 59 (3/4): 347–382, Bibcode:1985JLTP...59..347L, doi:10.1007/BF00683782, S2CID 120813342
- ^ Anderson, P. W. (1964), "Special Effects in Superconductivity", in Caianiello, E. R. (ed.), Lectures on the Many-Body Problem, Vol. 2, New York: Academic Press
- ^ Davidson, Ernest R. (1965-02-15). "On Derivations of the Uncertainty Principle". The Journal of Chemical Physics. 42 (4): 1461–1462. Bibcode:1965JChPh..42.1461D. doi:10.1063/1.1696139. ISSN 0021-9606. Archived from the original on 2024-02-23. Retrieved 2024-01-20.
- ^ Hall, B. C. (2013), Quantum Theory for Mathematicians, Springer, p. 245, Bibcode:2013qtm..book.....H
- ^ Hall, B. C. (2013), Quantum Theory for Mathematicians, Springer, p. 246, Bibcode:2013qtm..book.....H
- ^ Giovannetti, V.; Lloyd, S.; Maccone, L. (2011). "Advances in quantum metrology". Nature Photonics. 5 (4): 222. arXiv:1102.2318. Bibcode:2011NaPho...5..222G. doi:10.1038/nphoton.2011.35. S2CID 12591819.Giovannetti, V.; Lloyd, S.; Maccone, L. (2011). "Advances in quantum metrology". Nature Photonics. 5 (4): 222. arXiv:1102.2318. Bibcode:2011NaPho...5..222G. doi:10.1038/nphoton.2011.35. S2CID 12591819.arXiv Wayback Machine에서 아카이브된 2020-08-06
- ^ Luis, Alfredo (2017-03-13). "Breaking the weak Heisenberg limit". Physical Review A. 95 (3): 032113. arXiv:1607.07668. Bibcode:2017PhRvA..95c2113L. doi:10.1103/PhysRevA.95.032113. ISSN 2469-9926. S2CID 55838380.
- ^ Busch, P.; Lahti, P.; Werner, R. F. (2013). "Proof of Heisenberg's Error-Disturbance Relation". Physical Review Letters. 111 (16): 160405. arXiv:1306.1565. Bibcode:2013PhRvL.111p0405B. doi:10.1103/PhysRevLett.111.160405. PMID 24182239. S2CID 24507489.
- ^ Busch, P.; Lahti, P.; Werner, R. F. (2014). "Heisenberg uncertainty for qubit measurements". Physical Review A. 89 (1): 012129. arXiv:1311.0837. Bibcode:2014PhRvA..89a2129B. doi:10.1103/PhysRevA.89.012129. S2CID 118383022.
- ^ Erhart, J.; Sponar, S.; Sulyok, G.; Badurek, G.; Ozawa, M.; Hasegawa, Y. (2012). "Experimental demonstration of a universally valid error-disturbance uncertainty relation in spin measurements". Nature Physics. 8 (3): 185–189. arXiv:1201.1833. Bibcode:2012NatPh...8..185E. doi:10.1038/nphys2194. S2CID 117270618.
- ^ Baek, S.-Y.; Kaneda, F.; Ozawa, M.; Edamatsu, K. (2013). "Experimental violation and reformulation of the Heisenberg's error-disturbance uncertainty relation". Scientific Reports. 3: 2221. Bibcode:2013NatSR...3E2221B. doi:10.1038/srep02221. PMC 3713528. PMID 23860715.
- ^ Ringbauer, M.; Biggerstaff, D.N.; Broome, M.A.; Fedrizzi, A.; Branciard, C.; White, A.G. (2014). "Experimental Joint Quantum Measurements with Minimum Uncertainty". Physical Review Letters. 112 (2): 020401. arXiv:1308.5688. Bibcode:2014PhRvL.112b0401R. doi:10.1103/PhysRevLett.112.020401. PMID 24483993. S2CID 18730255.
- ^ Björk, G.; Söderholm, J.; Trifonov, A.; Tsegaye, T.; Karlsson, A. (1999). "Complementarity and the uncertainty relations". Physical Review. A60 (3): 1878. arXiv:quant-ph/9904069. Bibcode:1999PhRvA..60.1874B. doi:10.1103/PhysRevA.60.1874. S2CID 27371899.
- ^ Fujikawa, Kazuo (2012). "Universally valid Heisenberg uncertainty relation". Physical Review A. 85 (6): 062117. arXiv:1205.1360. Bibcode:2012PhRvA..85f2117F. doi:10.1103/PhysRevA.85.062117. S2CID 119640759.
- ^ Judge, D. (1964), "On the uncertainty relation for angle variables", Il Nuovo Cimento, 31 (2): 332–340, Bibcode:1964NCim...31..332J, doi:10.1007/BF02733639, S2CID 120553526
- ^ Bouten, M.; Maene, N.; Van Leuven, P. (1965), "On an uncertainty relation for angle variables", Il Nuovo Cimento, 37 (3): 1119–1125, Bibcode:1965NCim...37.1119B, doi:10.1007/BF02773197, S2CID 122838645
- ^ Louisell, W. H. (1963), "Amplitude and phase uncertainty relations", Physics Letters, 7 (1): 60–61, Bibcode:1963PhL.....7...60L, doi:10.1016/0031-9163(63)90442-6
- ^ DeWitt, B. S.; Graham, N. (1973), The Many-Worlds Interpretation of Quantum Mechanics, Princeton: Princeton University Press, pp. 52–53, ISBN 0-691-08126-3
- ^ Hirschman, I. I. Jr. (1957), "A note on entropy", American Journal of Mathematics, 79 (1): 152–156, doi:10.2307/2372390, JSTOR 2372390.
- ^ Beckner, W. (1975), "Inequalities in Fourier analysis", Annals of Mathematics, 102 (6): 159–182, doi:10.2307/1970980, JSTOR 1970980, PMC 432369, PMID 16592223.
- ^ Bialynicki-Birula, I.; Mycielski, J. (1975), "Uncertainty Relations for Information Entropy in Wave Mechanics", Communications in Mathematical Physics, 44 (2): 129–132, Bibcode:1975CMaPh..44..129B, doi:10.1007/BF01608825, S2CID 122277352, archived from the original on 2021-02-08, retrieved 2021-08-17
- ^ Huang, Yichen (24 May 2011). "Entropic uncertainty relations in multidimensional position and momentum spaces". Physical Review A. 83 (5): 052124. arXiv:1101.2944. Bibcode:2011PhRvA..83e2124H. doi:10.1103/PhysRevA.83.052124. S2CID 119243096.
- ^ Chafaï, D. (2003), "Gaussian maximum of entropy and reversed log-Sobolev inequality", Séminaire de Probabilités XXXVI, Lecture Notes in Mathematics, vol. 1801, pp. 194–200, arXiv:math/0102227, doi:10.1007/978-3-540-36107-7_5, ISBN 978-3-540-00072-3, S2CID 17795603
- ^ Chiew, Shao-Hen; Gessner, Manuel (31 January 2022). "Improving sum uncertainty relations with the quantum Fisher information". Physical Review Research. 4 (1): 013076. arXiv:2109.06900. Bibcode:2022PhRvR...4a3076C. doi:10.1103/PhysRevResearch.4.013076. S2CID 237513883.
- ^ Havin, V.; Jöricke, B. (1994), The Uncertainty Principle in Harmonic Analysis, Springer-Verlag
- ^ Folland, Gerald; Sitaram, Alladi (May 1997), "The Uncertainty Principle: A Mathematical Survey", Journal of Fourier Analysis and Applications, 3 (3): 207–238, doi:10.1007/BF02649110, MR 1448337, S2CID 121355943
- ^ Sitaram, A (2001) [1994], "Uncertainty principle, mathematical", Encyclopedia of Mathematics, EMS Press
- ^ 맷 홀, "가보르 불확실성 원칙이란?" 2018-02-09 Wayback Machine에서 보관
- ^ Donoho, D.L.; Stark, P.B (1989). "Uncertainty principles and signal recovery". SIAM Journal on Applied Mathematics. 49 (3): 906–931. doi:10.1137/0149053.
- ^ Terence Tao (2005), "An uncertainty principle for cyclic groups of prime order", Mathematical Research Letters, 12 (1): 121–127, arXiv:math/0308286, doi:10.4310/MRL.2005.v12.n1.a11, S2CID 8548232
- ^ Amrein, W.O.; Berthier, A.M. (1977), "On support properties of Lp-functions and their Fourier transforms", Journal of Functional Analysis, 24 (3): 258–267, doi:10.1016/0022-1236(77)90056-8.
- ^ Benedicks, M. (1985), "On Fourier transforms of functions supported on sets of finite Lebesgue measure", J. Math. Anal. Appl., 106 (1): 180–183, doi:10.1016/0022-247X(85)90140-4
- ^ Nazarov, F. (1994), "Local estimates for exponential polynomials and their applications to inequalities of the uncertainty principle type", St. Petersburg Math. J., 5: 663–717
- ^ Jaming, Ph. (2007), "Nazarov's uncertainty principles in higher dimension", J. Approx. Theory, 149 (1): 30–41, arXiv:math/0612367, doi:10.1016/j.jat.2007.04.005, S2CID 9794547
- ^ Hardy, G.H. (1933), "A theorem concerning Fourier transforms", Journal of the London Mathematical Society, 8 (3): 227–231, doi:10.1112/jlms/s1-8.3.227
- ^ Hörmander, L. (1991), "A uniqueness theorem of Beurling for Fourier transform pairs", Ark. Mat., 29 (1–2): 231–240, Bibcode:1991ArM....29..237H, doi:10.1007/BF02384339, S2CID 121375111
- ^ Bonami, A.; Demange, B.; Jaming, Ph. (2003), "Hermite functions and uncertainty principles for the Fourier and the windowed Fourier transforms", Rev. Mat. Iberoamericana, 19: 23–55, arXiv:math/0102111, Bibcode:2001math......2111B, doi:10.4171/RMI/337, S2CID 1211391
- ^ Hedenmalm, Haakan (2012), "Heisenberg's uncertainty principle in the sense of Beurling", Journal d'Analyse Mathématique, 118 (2): 691–702, arXiv:1203.5222, Bibcode:2012arXiv1203.5222H, doi:10.1007/s11854-012-0048-9, S2CID 54533890
- ^ Demange, Bruno (2009), Uncertainty Principles Associated to Non-degenerate Quadratic Forms, Société Mathématique de France, ISBN 978-2-85629-297-6
- ^ Whittaker, Edmund T. (1989). A history of the theories of aether & electricity. Vol. II: The modern theories, 1900–1926 (Repr ed.). New York: Dover Publ. p. 267. ISBN 978-0-486-26126-3.
- ^ "This Month in Physics History". www.aps.org. Archived from the original on 2011-01-30. Retrieved 2023-11-04.
- ^ a b c Heisenberg, W. (1930), Physikalische Prinzipien der Quantentheorie (in German), Leipzig: Hirzel 영어 번역 양자 이론의 물리적 원리 시카고: 1930년 시카고 대학교 출판부.
- ^ 하이젠베르크, W., 다이 피지크 더 아톰케른, 테일러 & 프란시스, 1952, p. 30.
- ^ Cassidy, David; Saperstein, Alvin M. (2009), "Beyond Uncertainty: Heisenberg, Quantum Physics, and the Bomb", Physics Today, New York: Bellevue Literary Press, 63 (1): 185, Bibcode:2010PhT....63a..49C, doi:10.1063/1.3293416, archived from the original on Jan 4, 2024
- ^ Greenstein, George; Zajonc, Arthur (2006). The Quantum Challenge: Modern Research on the Foundations of Quantum Mechanics. Jones & Bartlett Learning. ISBN 978-0-7637-2470-2.
- ^ Tipler, Paul A.; Llewellyn, Ralph A. (1999), Modern Physics, vol. 3, W.H. Freeman & Co., p. 3, ISBN 978-1572591646, LCCN 98046099
- ^ Enz, Charles Paul; von Meyenn, Karl (1994). Writings on Physics and Philosophy by Wolfgang Pauli. Translated by Robert Schlapp. Springer-Verlag. p. 43. ISBN 3-540-56859-X. Archived from the original on 2020-08-19. Retrieved 2018-02-10.
- ^ 파인먼 물리학 강의, 3권, 2-2
- ^ a b 가모우, G., 갈릴레오에서 아인슈타인에 이르는 위대한 물리학자들, 쿠리어 도버, 1988, p.260.
- ^ 쿠마르, M., 퀀텀: 아인슈타인, 보어와 현실의 본질에 관한 위대한 논쟁, 아이콘, 2009, p. 282.
- ^ 가모우, G., 갈릴레오에서 아인슈타인에 이르는 위대한 물리학자들, 쿠리어 도버, 1988, 페이지 260-261.[ISBN missing]
- ^ 쿠마르, M., 퀀텀: 아인슈타인, 보어와 현실의 본질에 관한 위대한 논쟁, 아이콘, 2009, p. 287.
- ^ Einstein, A.; Podolsky, B.; Rosen, N. (1935-05-15). "Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?". Physical Review. 47 (10): 777–780. Bibcode:1935PhRv...47..777E. doi:10.1103/PhysRev.47.777.
- ^ Kumar, Manjit (2011). Quantum: Einstein, Bohr and the great debate about the nature of reality (1st pbk. ed.). New York: Norton. ISBN 978-0-393-33988-8.
- ^ a b c Popper, Karl (1959), The Logic of Scientific Discovery, Hutchinson & Co.
- ^ Jarvie, Ian Charles; Milford, Karl; Miller, David W (2006), Karl Popper: a centenary assessment, vol. 3, Ashgate Publishing, ISBN 978-0-7546-5712-5
- ^ Popper, Karl; Carl Friedrich von Weizsäcker (1934), "Zur Kritik der Ungenauigkeitsrelationen (Critique of the Uncertainty Relations)", Naturwissenschaften, 22 (48): 807–808, Bibcode:1934NW.....22..807P, doi:10.1007/BF01496543, S2CID 40843068.
- ^ 포퍼, K. 양자 이론과 물리학에서의 분열, 언윈 하이먼, 1982, pp. 53-54.
- ^ Mehra, Jagdish; Rechenberg, Helmut (2001), The Historical Development of Quantum Theory, Springer, ISBN 978-0-387-95086-0
- ^ Compton, A. H. (1931). "The Uncertainty Principle and Free Will". Science. 74 (1911): 172. Bibcode:1931Sci....74..172C. doi:10.1126/science.74.1911.172. PMID 17808216. S2CID 29126625.
- ^ Heisenberg, M. (2009). "Is free will an illusion?". Nature. 459 (7244): 164–165. Bibcode:2009Natur.459..164H. doi:10.1038/459164a. PMID 19444190. S2CID 4420023.
- ^ a b Davies, P.C.W. (2004). "Does quantum mechanics play a non-trivial role in life?". Biosystems. 78 (1–3): 69–79. Bibcode:2004BiSys..78...69D. doi:10.1016/j.biosystems.2004.07.001. PMID 15555759.
- ^ Hänggi, Esther; Wehner, Stephanie (2013). "A violation of the uncertainty principle implies a violation of the second law of thermodynamics". Nature Communications. 4: 1670. arXiv:1205.6894. Bibcode:2013NatCo...4.1670H. doi:10.1038/ncomms2665. PMID 23575674. S2CID 205316392.
- ^ 켐블, E. C., 1937, 양자역학의 기본원리(McGraw-Hill, New York; Dover에 의해 재인쇄됨), 244페이지
- ^ Haag, R. (1996), 국소 양자 물리학: 필드, 입자, 대수, (베를린: 스프링어)[page needed][ISBN missing]
- ^ Peres, Asher; Terno, Daniel R. (2004-01-06). "Quantum information and relativity theory". Reviews of Modern Physics. 76 (1): 93–123 [111]. arXiv:quant-ph/0212023. Bibcode:2004RvMP...76...93P. doi:10.1103/RevModPhys.76.93. ISSN 0034-6861. S2CID 7481797. Archived from the original on 2024-02-23. Retrieved 2024-01-25.
- ^ Elion, W. J.; Matters, M.; Geigenmüller, U.; Mooij, J. E. (1994), "Direct demonstration of Heisenberg's uncertainty principle in a superconductor", Nature, 371 (6498): 594–595, Bibcode:1994Natur.371..594E, doi:10.1038/371594a0, S2CID 4240085
- ^ Smithey, D. T.; M. Beck, J. Cooper, M. G. Raymer; Cooper, J.; Raymer, M. G. (1993), "Measurement of number–phase uncertainty relations of optical fields", Phys. Rev. A, 48 (4): 3159–3167, Bibcode:1993PhRvA..48.3159S, doi:10.1103/PhysRevA.48.3159, PMID 9909968
{{citation}}: CS1 maint: 다중 이름: 작성자 목록(링크) - ^ Caves, Carlton (1981), "Quantum-mechanical noise in an interferometer", Phys. Rev. D, 23 (8): 1693–1708, Bibcode:1981PhRvD..23.1693C, doi:10.1103/PhysRevD.23.1693





![{\displaystyle \operatorname {P} [a\leq X\leq b]=\int _{a}^{b}|\psi (x)|^{2}\,\mathrm {d} x~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8852ff1f2e7c518fce8dfbb77f8e8a7920c63f3)








![{\displaystyle {\begin{aligned}g(x)&={\frac {1}{\sqrt {2\pi \hbar }}}\cdot \int _{-\infty }^{\infty }{\tilde {g}}(p)\cdot e^{ipx/\hbar }\,dp\\&={\frac {1}{\sqrt {2\pi \hbar }}}\int _{-\infty }^{\infty }p\cdot \varphi (p)\cdot e^{ipx/\hbar }\,dp\\&={\frac {1}{2\pi \hbar }}\int _{-\infty }^{\infty }\left[p\cdot \int _{-\infty }^{\infty }\psi (\chi )e^{-ip\chi /\hbar }\,d\chi \right]\cdot e^{ipx/\hbar }\,dp\\&={\frac {i}{2\pi }}\int _{-\infty }^{\infty }\left[{\cancel {\left.\psi (\chi )e^{-ip\chi /\hbar }\right|_{-\infty }^{\infty }}}-\int _{-\infty }^{\infty }{\frac {d\psi (\chi )}{d\chi }}e^{-ip\chi /\hbar }\,d\chi \right]\cdot e^{ipx/\hbar }\,dp\\&={\frac {-i}{2\pi }}\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }{\frac {d\psi (\chi )}{d\chi }}e^{-ip\chi /\hbar }\,d\chi \,e^{ipx/\hbar }\,dp\\&=\left(-i\hbar {\frac {d}{dx}}\right)\cdot \psi (x),\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/42db5a07d8c895b1e9caffa2cde0b6df608ec8f8)




![{\displaystyle {\begin{aligned}\langle f\mid g\rangle -\langle g\mid f\rangle ={}&\int _{-\infty }^{\infty }\psi ^{*}(x)\,x\cdot \left(-i\hbar {\frac {d}{dx}}\right)\,\psi (x)\,dx\\&{}-\int _{-\infty }^{\infty }\psi ^{*}(x)\,\left(-i\hbar {\frac {d}{dx}}\right)\cdot x\,\psi (x)\,dx\\={}&i\hbar \cdot \int _{-\infty }^{\infty }\psi ^{*}(x)\left[\left(-x\cdot {\frac {d\psi (x)}{dx}}\right)+{\frac {d(x\psi (x))}{dx}}\right]\,dx\\={}&i\hbar \cdot \int _{-\infty }^{\infty }\psi ^{*}(x)\left[\left(-x\cdot {\frac {d\psi (x)}{dx}}\right)+\psi (x)+\left(x\cdot {\frac {d\psi (x)}{dx}}\right)\right]\,dx\\={}&i\hbar \cdot \int _{-\infty }^{\infty }\psi ^{*}(x)\psi (x)\,dx\\={}&i\hbar \cdot \int _{-\infty }^{\infty }|\psi (x)|^{2}\,dx\\={}&i\hbar \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4ddead3f7e2d237c2ad9bb5258ad66a9d92c599)


![{\displaystyle [{\hat {A}},{\hat {B}}]={\hat {A}}{\hat {B}}-{\hat {B}}{\hat {A}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3133da214f8f0fcf1ba11e907cfd121a2179b1b4)
![{\displaystyle [{\hat {x}},{\hat {p}}]=i\hbar .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fee0861ae7784cb51a1b43f6c51735c22c23274e)
![{\displaystyle [{\hat {x}},{\hat {p}}]|\psi \rangle =({\hat {x}}{\hat {p}}-{\hat {p}}{\hat {x}})|\psi \rangle =({\hat {x}}-x_{0}{\hat {I}}){\hat {p}}\,|\psi \rangle =i\hbar |\psi \rangle ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8255257353e4743e966c106dea5674689ed04690)

![{\displaystyle [{\hat {x}},{\hat {p}}]|\psi \rangle =i\hbar |\psi \rangle \neq 0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04d341bbd1c29d8f96a5ce5ad6e2cf856d1b1f40)







































![{\displaystyle {\frac {d\langle {\hat {B}}\rangle }{dt}}={\frac {i}{\hbar }}\langle [{\hat {H}},{\hat {B}}]\rangle .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92bca95fec448b2e3291ae56caf76d1796e6c02f)
![{\displaystyle \sigma _{H}\sigma _{B}\geq \left|{\frac {1}{2i}}\langle [{\hat {H}},{\hat {B}}]\rangle \right|,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48c8d45afe6c1f61a750dbb97358c10dde03f8fb)







![{\displaystyle [{\hat {A}},{\hat {B}}]={\hat {A}}{\hat {B}}-{\hat {B}}{\hat {A}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9814a77ea436e956fd7abaad7b5906457037b565)
![{\displaystyle \sigma _{A}\sigma _{B}\geq \left|{\frac {1}{2i}}\langle [{\hat {A}},{\hat {B}}]\rangle \right|={\frac {1}{2}}\left|\langle [{\hat {A}},{\hat {B}}]\rangle \right|,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e237cc47d6a6ffaf614f696672356c362f84ac0)
![{\displaystyle \sigma _{A}^{2}\sigma _{B}^{2}\geq \left|{\frac {1}{2}}\langle \{{\hat {A}},{\hat {B}}\}\rangle -\langle {\hat {A}}\rangle \langle {\hat {B}}\rangle \right|^{2}+\left|{\frac {1}{2i}}\langle [{\hat {A}},{\hat {B}}]\rangle \right|^{2},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/81d7a893fe43757553fb6a3e5a51cdb83290aadd)









![{\displaystyle {\begin{aligned}\langle f\mid g\rangle &=\langle \Psi |({\hat {A}}-\langle {\hat {A}}\rangle )({\hat {B}}-\langle {\hat {B}}\rangle )\Psi \rangle \\[4pt]&=\langle \Psi \mid ({\hat {A}}{\hat {B}}-{\hat {A}}\langle {\hat {B}}\rangle -{\hat {B}}\langle {\hat {A}}\rangle +\langle {\hat {A}}\rangle \langle {\hat {B}}\rangle )\Psi \rangle \\[4pt]&=\langle \Psi \mid {\hat {A}}{\hat {B}}\Psi \rangle -\langle \Psi \mid {\hat {A}}\langle {\hat {B}}\rangle \Psi \rangle -\langle \Psi \mid {\hat {B}}\langle {\hat {A}}\rangle \Psi \rangle +\langle \Psi \mid \langle {\hat {A}}\rangle \langle {\hat {B}}\rangle \Psi \rangle \\[4pt]&=\langle {\hat {A}}{\hat {B}}\rangle -\langle {\hat {A}}\rangle \langle {\hat {B}}\rangle -\langle {\hat {A}}\rangle \langle {\hat {B}}\rangle +\langle {\hat {A}}\rangle \langle {\hat {B}}\rangle \\[4pt]&=\langle {\hat {A}}{\hat {B}}\rangle -\langle {\hat {A}}\rangle \langle {\hat {B}}\rangle .\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e8c0c05428ab53be785878d1546c265c45c6e755)
![{\displaystyle \langle f\mid g\rangle -\langle g\mid f\rangle =\langle {\hat {A}}{\hat {B}}\rangle -\langle {\hat {A}}\rangle \langle {\hat {B}}\rangle -\langle {\hat {B}}{\hat {A}}\rangle +\langle {\hat {A}}\rangle \langle {\hat {B}}\rangle =\langle [{\hat {A}},{\hat {B}}]\rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/eaf12a5caf8e73c4e1cfdfbbf3ebb1c3e32e7e0f)

![{\displaystyle |\langle f\mid g\rangle |^{2}={\Big (}{\frac {1}{2}}\langle \{{\hat {A}},{\hat {B}}\}\rangle -\langle {\hat {A}}\rangle \langle {\hat {B}}\rangle {\Big )}^{2}+{\Big (}{\frac {1}{2i}}\langle [{\hat {A}},{\hat {B}}]\rangle {\Big )}^{2}\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/074cd206c3b6789fd747fa2efa892ea596651470)
![{\displaystyle \sigma _{A}\sigma _{B}\geq {\sqrt {{\Big (}{\frac {1}{2}}\langle \{{\hat {A}},{\hat {B}}\}\rangle -\langle {\hat {A}}\rangle \langle {\hat {B}}\rangle {\Big )}^{2}+{\Big (}{\frac {1}{2i}}\langle [{\hat {A}},{\hat {B}}]\rangle {\Big )}^{2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/96a2a724edaa3e9b3e175f7de8158b796bef58c0)
![{\displaystyle \sigma _{A}^{2}\sigma _{B}^{2}\geq \left|{\frac {1}{2}}\operatorname {tr} (\rho \{A,B\})-\operatorname {tr} (\rho A)\operatorname {tr} (\rho B)\right|^{2}+\left|{\frac {1}{2i}}\operatorname {tr} (\rho [A,B])\right|^{2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8271822251517d5a4e6879ea287fd36556a95e8)


![{\displaystyle \sigma _{A}^{2}+\sigma _{B}^{2}\geq \pm i\langle \Psi \mid [A,B]|\Psi \rangle +\mid \langle \Psi \mid (A\pm iB)\mid {\bar {\Psi }}\rangle |^{2},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe87035b4463c5578ccda71d74b8e7c9fd627515)
![{\displaystyle \pm i\langle \Psi \mid [A,B]\mid \Psi \rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a34a5250780e2a23b4befafff39d5522cc8266c)



![{\displaystyle \sigma _{A}^{2}\sigma _{B}^{2}\geq \left[\sum _{k}p_{k}L(\varrho _{k})\right]^{2},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe2197885d47337c2e848acc051efdea71b02870)
![{\displaystyle L(\varrho )={\sqrt {\left|{\frac {1}{2}}\operatorname {tr} (\rho \{A,B\})-\operatorname {tr} (\rho A)\operatorname {tr} (\rho B)\right|^{2}+\left|{\frac {1}{2i}}\operatorname {tr} (\rho [A,B])\right|^{2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9217563cc15d7b37797888126f4b4c44b7f19c08)
![{\displaystyle \sigma _{A}^{2}\sigma _{B}^{2}\geq \left[\max _{p_{k},\varrho _{k}}\sum _{k}p_{k}L(\varrho _{k})\right]^{2},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98f249b302c95aa4be14de7ec6f82ffb5f169d5e)
![{\displaystyle \sigma _{A}^{2}F_{Q}[\varrho ,B]\geq 4\left[\min _{p_{k},\Psi _{k}}\sum _{k}p_{k}L(\vert \Psi _{k}\rangle \langle \Psi _{k}\vert )\right]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58902ccc3a0b70047c4db2a60db2c59e012fd34f)

![{\displaystyle \sigma _{A}^{2}F_{Q}[\varrho ,B]\geq \vert \langle i[A,B]\rangle \vert ^{2},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c25345e515fab68aaa473847b0f644f1d1b0965a)
![{\displaystyle F_{Q}[\varrho ,B]\leq 4\sigma _{B},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76b697790877dcd32b480f16ef3565113c062e83)






![{\displaystyle [J_{x},J_{y}]=i\hbar \varepsilon _{xyz}J_{z}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92feb40a1e1bb732beffa55c687ccfbcec8ff007)





![{\displaystyle {\hat {A}}\psi (\theta )=\theta \psi (\theta ),\quad \theta \in [0,2\pi ],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f85b2a63d69030bd4deabafe7641563413b8ec23)





![{\displaystyle \varepsilon _{A}\,\eta _{B}+\varepsilon _{A}\,\sigma _{B}+\sigma _{A}\,\eta _{B}\,\geq \,{\frac {1}{2}}\,\left|{\Bigl \langle }{\bigl [}{\hat {A}},{\hat {B}}{\bigr ]}{\Bigr \rangle }\right|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e07b031a15d10a6380f7ee47da5c5c1dfb93e31a)
![{\displaystyle \varepsilon _{A}\,\eta _{B}\,\geq \,{\frac {1}{2}}\,\left|{\Bigl \langle }{\bigl [}{\hat {A}},{\hat {B}}{\bigr ]}{\Bigr \rangle }\right|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/28d08057de34306115c996b9943fb0603282befc)
![{\displaystyle \varepsilon _{A}\,\varepsilon _{B}\,\geq \,{\frac {1}{2}}\,\left|{\Bigl \langle }{\bigl [}{\hat {A}},{\hat {B}}{\bigr ]}{\Bigr \rangle }\right|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8f93231686a00ca50485a5eccdadddfbc4f6b2c3)
![{\displaystyle \sigma _{A}\,\sigma _{B}\,\geq \,{\frac {1}{2}}\,\left|{\Bigl \langle }{\bigl [}{\hat {A}},{\hat {B}}{\bigr ]}{\Bigr \rangle }\right|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1606cabaad53903e8110417fff05ebda20a2dd41)
![{\displaystyle \varepsilon _{A}\eta _{B}+\varepsilon _{A}\,\sigma _{B}+\sigma _{A}\,\eta _{B}+\sigma _{A}\sigma _{B}\geq \left|{\Bigl \langle }{\bigl [}{\hat {A}},{\hat {B}}{\bigr ]}{\Bigr \rangle }\right|.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99801a6fd6e9d9f36223cce7aba8a30cf39e6230)
![{\displaystyle (\varepsilon _{A}+\sigma _{A})\,(\eta _{B}+\sigma _{B})\,\geq \,\left|{\Bigl \langle }{\bigl [}{\hat {A}},{\hat {B}}{\bigr ]}{\Bigr \rangle }\right|.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ec1acc4af7b675c838b09fc719057c5d16819c4)


![{\displaystyle {\bar {\varepsilon }}_{A}\,{\bar {\eta }}_{B}\,\geq \,\left|{\Bigl \langle }{\bigl [}{\hat {A}},{\hat {B}}{\bigr ]}{\Bigr \rangle }\right|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb507c6e7fa92a94bfb07f979999ccbb5ac7450a)

















![{\displaystyle {\begin{aligned}H_{x}&=-\int |\psi (x)|^{2}\ln(|\psi (x)|^{2}\cdot x_{0})\,dx\\&=-{\frac {1}{x_{0}{\sqrt {2\pi }}}}\int _{-\infty }^{\infty }\exp {\left(-{\frac {x^{2}}{2x_{0}^{2}}}\right)}\ln \left[{\frac {1}{\sqrt {2\pi }}}\exp {\left(-{\frac {x^{2}}{2x_{0}^{2}}}\right)}\right]\,dx\\&={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }\exp {\left(-{\frac {u^{2}}{2}}\right)}\left[\ln({\sqrt {2\pi }})+{\frac {u^{2}}{2}}\right]\,du\\&=\ln({\sqrt {2\pi }})+{\frac {1}{2}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/124b7c9778e717ecae5fb23df17a3e6ea1cdab89)


![{\displaystyle {\begin{aligned}H_{p}&=-\int |\varphi (p)|^{2}\ln(|\varphi (p)|^{2}\cdot \hbar /x_{0})\,dp\\&=-{\sqrt {\frac {2x_{0}^{2}}{\pi \hbar ^{2}}}}\int _{-\infty }^{\infty }\exp {\left(-{\frac {2x_{0}^{2}p^{2}}{\hbar ^{2}}}\right)}\ln \left[{\sqrt {\frac {2}{\pi }}}\exp {\left(-{\frac {2x_{0}^{2}p^{2}}{\hbar ^{2}}}\right)}\right]\,dp\\&={\sqrt {\frac {2}{\pi }}}\int _{-\infty }^{\infty }\exp {\left(-2v^{2}\right)}\left[\ln \left({\sqrt {\frac {\pi }{2}}}\right)+2v^{2}\right]\,dv\\&=\ln \left({\sqrt {\frac {\pi }{2}}}\right)+{\frac {1}{2}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8106bc906d97851869d4000e4d3d0dd8e7916e56)

![{\displaystyle \operatorname {P} [x_{j}]=\int _{(j-1/2)\delta x-c}^{(j+1/2)\delta x-c}|\psi (x)|^{2}\,dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7c173529c81593fd8c2e56a4e1af15f369c365c)
![{\displaystyle H_{x}=-\sum _{j=-\infty }^{\infty }\operatorname {P} [x_{j}]\ln \operatorname {P} [x_{j}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25c2fd9ede05e0615e6eff1a8f2ace626debd818)


![{\displaystyle {\begin{aligned}\operatorname {P} [x_{j}]&={\sqrt {\frac {m\omega }{\pi \hbar }}}\int _{(j-1/2)\delta x}^{(j+1/2)\delta x}\exp \left(-{\frac {m\omega x^{2}}{\hbar }}\right)\,dx\\&={\sqrt {\frac {1}{\pi }}}\int _{(j-1/2)\delta x{\sqrt {m\omega /\hbar }}}^{(j+1/2)\delta x{\sqrt {m\omega /\hbar }}}e^{u^{2}}\,du\\&={\frac {1}{2}}\left[\operatorname {erf} \left(\left(j+{\frac {1}{2}}\right)\delta x\cdot {\sqrt {\frac {m\omega }{\hbar }}}\right)-\operatorname {erf} \left(\left(j-{\frac {1}{2}}\right)\delta x\cdot {\sqrt {\frac {m\omega }{\hbar }}}\right)\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb98a69e46b2d10143459959d1679c78443b6378)
![{\displaystyle \operatorname {P} [p_{j}]={\frac {1}{2}}\left[\operatorname {erf} \left(\left(j+{\frac {1}{2}}\right)\delta p\cdot {\frac {1}{\sqrt {\hbar m\omega }}}\right)-\operatorname {erf} \left(\left(j-{\frac {1}{2}}\right)\delta x\cdot {\frac {1}{\sqrt {\hbar m\omega }}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed784fa900105bac03e1163a54fc3dd5732367aa)


![{\displaystyle \operatorname {P} [x_{j}]=\operatorname {P} [p_{j}]={\frac {1}{2}}\left[\operatorname {erf} \left(\left(j+{\frac {1}{2}}\right){\sqrt {2\pi }}\right)-\operatorname {erf} \left(\left(j-{\frac {1}{2}}\right){\sqrt {2\pi }}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba65e2143152330bf233c24e6524ac16a365c168)
![{\displaystyle {\begin{aligned}H_{x}=H_{p}&=-\sum _{j=-\infty }^{\infty }\operatorname {P} [x_{j}]\ln \operatorname {P} [x_{j}]\\&=-\sum _{j=-\infty }^{\infty }{\frac {1}{2}}\left[\operatorname {erf} \left(\left(j+{\frac {1}{2}}\right){\sqrt {2\pi }}\right)-\operatorname {erf} \left(\left(j-{\frac {1}{2}}\right){\sqrt {2\pi }}\right)\right]\ln {\frac {1}{2}}\left[\operatorname {erf} \left(\left(j+{\frac {1}{2}}\right){\sqrt {2\pi }}\right)-\operatorname {erf} \left(\left(j-{\frac {1}{2}}\right){\sqrt {2\pi }}\right)\right]\\&\approx 0.3226\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce13d4ff28b796ec3e3206a6d32b1c3eff5d693a)

![{\displaystyle \psi (x)={\begin{cases}{1}/{\sqrt {2a}}&{\text{for }}|x|\leq a,\\[8pt]0&{\text{for }}|x|>a\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6252d65b527d2b4bf3a708c339d7907976267c45)

![{\displaystyle \operatorname {P} [x_{0}]=\int _{-a}^{0}{\frac {1}{2a}}\,dx={\frac {1}{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4bb8e8e07cba14e44ac3fd1f812c87b344f79978)
![{\displaystyle \operatorname {P} [x_{1}]=\int _{0}^{a}{\frac {1}{2a}}\,dx={\frac {1}{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/abb619286fac29cd04fb8ad539e4d7fc979da3fd)
![{\displaystyle H_{x}=-\sum _{j=0}^{1}\operatorname {P} [x_{j}]\ln \operatorname {P} [x_{j}]=-{\frac {1}{2}}\ln {\frac {1}{2}}-{\frac {1}{2}}\ln {\frac {1}{2}}=\ln 2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd49a257fd5578026bd28e8e539dccfaae24dd1f)
![{\displaystyle {\begin{aligned}\operatorname {P} [p_{j}]&={\frac {a}{\pi \hbar }}\int _{(j-1/2)\delta p}^{(j+1/2)\delta p}\operatorname {sinc} ^{2}\left({\frac {ap}{\hbar }}\right)\,dp\\&={\frac {1}{\pi }}\int _{2\pi (j-1/2)}^{2\pi (j+1/2)}\operatorname {sinc} ^{2}(u)\,du\\&={\frac {1}{\pi }}\left[\operatorname {Si} ((4j+2)\pi )-\operatorname {Si} ((4j-2)\pi )\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c11b911bee6171d2a7ac1ee1c5522d49625ffb2)
![{\displaystyle H_{p}=-\sum _{j=-\infty }^{\infty }\operatorname {P} [p_{j}]\ln \operatorname {P} [p_{j}]=-\operatorname {P} [p_{0}]\ln \operatorname {P} [p_{0}]-2\cdot \sum _{j=1}^{\infty }\operatorname {P} [p_{j}]\ln \operatorname {P} [p_{j}]\approx 0.53}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae44da862dea854275b063fc3b5fe01bd3f3309f)



 각운동량 성분입니다. 관계는 다음에서 도출할 수 있습니다.
각운동량 성분입니다. 관계는 다음에서 도출할 수 있습니다. 

![{\displaystyle \sigma _{J_{x}}^{2}+\sigma _{J_{y}}^{2}+F_{Q}[\varrho ,J_{z}]/4\geq j,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8a1b42fce2b1dd5c19fff569af0ffa3207ed373)