주장 프레임워크

인공지능과 관련 분야에서 논쟁 프레임워크는 논쟁적인 정보를 다루고 형식화된 주장을 사용하여 그것으로부터 결론을 도출하는 방법이다.

추상적 주장 프레임워크에서,^[1] 엔트리 레벨 정보는 예를 들어 데이터나 제안을 나타내는 추상적 논쟁의 집합이다. 인수 간의 충돌은 인수 집합에서 이진 관계로 표현된다. 구체적인 용어로, 당신은 지시된 그래프로 논쟁 프레임워크를 나타내는데, 노드가 인수이고 화살표는 공격 관계를 나타낸다. 던의 프레임워크에는 논리 기반 주장 프레임워크나^[2] 가치 기반 주장 프레임워크와 같은 몇 가지 확장이 존재한다.^[3]

추상적 논거 프레임워크

형식 프레임워크

추상적 주장 프레임워크(a la Dung)라고도 하며, 공식적으로 다음과 같은 쌍으로 정의된다.

• $인수$라고 하는 추상 요소 집합, A ${\displaystyle A}$을(를) 나타냄
• 공격 관계라고$하는$ A {\$displaystyle$ A$}$의 이진 관계에서 $R{\displaystyle }$ ${\displaystyle R}$이(가$)$ 표시됨

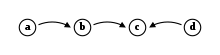
For instance, the argumentation system ${\displaystyle S=\langle A,R\rangle }$ with ${\displaystyle A=\{a,b,c,d\}}$ and ${\displaystyle R=\{(a,b),(b,c),(d,c)\}}$ contains four arguments (${\displaystyle a,b,c}$ and ${\displaystyle$$d}$) 및 세 가지 공격$({\displaystyle$ $a$$}$ ${\displaystyle }$ $b{\displaystyle }$ ${\displaystyle$ b$\},$ b ${\displaystyle b}$ $공격$ $c{\displaystyle }$ ${\displaystyle c}$ 및$$ $d{\displaystyle }$ ${\displaystyle d}$ $공격$ c ${\\displaystyle c}).$

똥은 몇 가지 관념을 정의한다.

• an argument ${\displaystyle a\in A}$ is acceptable with respect to ${\displaystyle E\subseteq A}$ if and only if ${\displaystyle E}$ defends ${\displaystyle a}$, that is ${\displaystyle \forall b\in A}$ such that ${\displaystyle (b,a)\in R,\exists c\in E}$ such that ${\displaystyle (c}$, ${\displaystyle b}$) ${\displaystyle \in }$ R ${\displaystyle (c,b)\in$ R$\},$
• 일련의 주장 $E{\displaystyle }$ ${\displaystyle E}$은(는${\displaystyle )}$ 그 주장 사이에 공격이 없으면 충돌하지 ${\displaystyle \mathrm{않는다<img\; alt="E"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/4232c9de2ee3eec0a9c0a19b15ab92daa6223f9b"\; style="vertical-align:\; -0.338ex;\; width:1.776ex;\; height:2.176ex;"\; papago-attr-id="71">}}$. ${\displaystyle \mathrm{형식적}}$으로: $\forall {\displaystyle \mathrm{}}$ ${\displaystyle a,}$ b, ${\displaystyle \in }$ E${\displaystyle }$,${\displaystyle }$(${\displaystyle b}$)${\displaystyle }$) R {\$displaystyle \ forall a,b\in$E$,$ $(a,b)\in$ R$},$ not $\in$ R$\},$
• 일련의 $주장{\displaystyle }$E {\$displaystyle$ E$}$은(는) 충돌이 없고 모든 주장이$$ E$${\$displaystyle$ E$\}$에 대해 허용되는 경우에만 허용된다.

수용의 다른 의미론

확장

어떤 주장이 받아들여질 수 있는지, 혹은 여러 개의 주장이 함께 받아들여질 수 있는지를 결정하기 위해, 둥은 주장 시스템이 주어진, 일련의 주장들(확장이라고 함)을 계산할 수 있도록 허용하는 몇 가지 수용의 의미론을 정의한다. 예를 들어, ${\displaystyle \mathrm{주어진}}$ $S{\displaystyle }$= ${\displaystyle ⟨}$ A${\displaystyle }$, ${\displaystyle R}$ ${\displaystyle ⟩}$ ${\displaystyle$ S$=\langle A,R\angle$ $\},$

• ${\displaystyle E}$ ${\displaystyle E}$은(는) 허용 가능한 집합이고 E ${\displaystyle E}$에 대한 모든 허용 가능한$$ $인수$가 E {\displaystyle E}에 속하는 경우에만$$ $S{\displaystyle }$ ${\displaystyle$ $S}$의 전체$확장$입니다$.$
• ${\displaystyle E}$ ${\displaystyle E}$은(는) $S{\displaystyle }$ ${\displaystyle S}$과(와) 관련하여 허용 가능한 세트 중 최대 요소인 경우에만$$ $S{\displaystyle }$ ${\displaystyle S}$의 기본 확장이다$.$
• ${\displaystyle E}$ is a stable extension of ${\displaystyle S}$ only if it is a conflict-free set that attacks every argument that does not belong in ${\displaystyle E}$ (formally, ${\displaystyle \forall a\in A\backslash E,\exists b\in E}$ such that ${\displaystyle (b,a)\in R}$$$,
• ${\displaystyle E}$ ${\displaystyle E}$은(는) $S{\displaystyle }$ ${\displaystyle S}$의 전체 확장 중 가장 작은 요소(설정 포함에 관한)인 경우에만$$ $S{\displaystyle }$ ${\displaystyle S}$의 (유일한) 접지 확장이다$.$

이러한 의미론으로 구축된 확장 집합 사이에는 다음과 같은 몇 가지 포함이 있다.

• 모든 안정적 확장이 선호되며
• 모든 선호 연장이 완료되고
• 접지 연장 완료,
• 만약 그 제도는 근거가 충분한( 없는 무한한 순서를 0,1,…, 오빠, 때문에{\displaystyle a_{0}일 경우 ,a_{1},\dots{}n},\dots ,a_ 전입니다. ∀ 같은;0,( 나는+1, 나는 존재하)∈ R{\displaystyle \forall i>, 0,(a_{i+1},a_{나는})\in R}), 이 모든 의미 coincide—only 한번 연장한 근거로 하고 있고, 안정적이며, 선호하는., 완성의

몇몇 다른 의미론들이 정의되었다.^[4]

$하나$는 시스템 $S{\displaystyle }$ ${\$$displaystyle \sigma$ \sigma \sigma } -확장$$ 시스템 S {\displaystyle S$}$의 집합을 주목하기 위해$$ ${\displaystyle \mathrm{표기법}}$ E x ${\displaystyle {}_{}}$ ${\displaystyle {\sigma }_{}}$($){\$$displaystyle Ext_${\sigma $}(S$$)$을 도입한다$.$

위 그림의$$ 시스템 $S{\displaystyle }$ ${\displaystyle S}$의 경우, 모든 Dung의 의미에 대해$$ E ${\displaystyle x}$ ${\displaystyle {}_{}}$ ${\displaystyle {\sigma }_{}S}$ ${\displaystyle )}$=${\displaystyle }${${\displaystyle a}$, ${\displaystyle d}$} ${\displaystyle Ext_{\sigma }=\\\\{a,d\}\}\}\}}}}}}}}}.$ 시스템은 근거가 충분하다. 그래서 의미론들이 일치하고, 받아들여지는 $주장$은 다음과 같다: ${\displaystyle a}$과 $d{\displaystyle }$ ${\displaystyle d$

라벨링스

라벨링은 논거의 수용을 표현하기 위한 확장보다 더 표현적인 방법이다. 구체적으로, 라벨 표시는 모든 주장을 (논의가 받아들여진다), 아웃(논의가 거부된다), 불문(논의가 정의되지 않는다, 받아들여지거나 거부되지 않는다)의 라벨과 연관시키는 매핑이다. 또한 쌍$({\displaystyle }$r g ${\displaystyle \mathit{u}}$ ${\displaystyle \mathit{m}}$ e ${\displaystyle \mathit{n}}$ ${\displaystyle \mathit{t},}$ ${\displaystyle l\mathit{}}$ ${\displaystyle \mathit{a}}$ ${\displaystyle \mathit{e}}$ ${\displaystyle \mathit{l}}$ $){\displaystyle({\mathitt{argument},{\mathitt{label})}}$의 집합으로 라벨을 표시할 수도 있다$.$

그러한 매핑은 추가적인 제약이 없으면 의미가 없다. 복직 라벨 표시의 개념은 지도 제작의 감각을 보장한다. ${\displaystyle L}$ ${\displaystyle L}$은(는$$) 다음과 $같은{\displaystyle }$ 경우에만 ${\displaystyle \mathrm{시스템}}$ S ${\displaystyle =,}$ ${\displaystyle A}$, R$display$ {\$displaystyle S$=\$langle$ A$,R\rangele$}에 복원 레이블을 표시하는 것이다$$.

• ${\displaystyle \forall a\in A,L(a)={\mathit {in}}}$ if and only if ${\displaystyle \forall b\in A}$ such that ${\displaystyle (b,a)\in R,L(b)={\mathit {out}}}$
• ${\displaystyle \forall a\in A,L(a)={\mathit {out}}}$ if and only if ${\displaystyle \exists b\in A}$ such that ${\displaystyle (b,a)\in R}$ and ${\displaystyle L(b)={\mathit {in}}}$
• ${\displaystyle \forall a\in A,L(a)={\mathit {undec}}}$ if and only if ${\displaystyle L(a)\neq {\mathit {in}}}$ and ${\displaystyle L(a)\neq {\mathit {out}}}$

모든 연장을 복직 라벨로 바꿀 수 있다: 연장의 논쟁은 들어왔고, 연장의 논쟁에 의해 공격당한 사람들은 빠져 나왔으며, 다른 사람들은 불경하다. 반대로, 사람들은 단지 논쟁을 계속하는 것만으로 복직 라벨 표시로부터 연장을 만들 수 있다. 실제로 카미나다는^[5] 복직 작업과 전체 연장이 비주류적인 방법으로 지도화될 수 있다는 것을 증명했다. 게다가, 다른 다퉁의 의미론들은 몇몇 특정한 복원 연구와 연관될 수 있다.

복직 실험은 받아들여지지 않은 주장과 정의되지 않은 주장으로부터 공격을 받기 때문에 받아들여지지 않은 주장들을 구분한다. 즉, 옹호되지 않는 주장들은 스스로를 방어할 수 없다. 논쟁은 적어도 또 다른 불경한 사람의 공격을 받는다면 불경하다. 밖에 나와 있는 논쟁으로만 공격받으면 반드시 안에 들어가야 하고, 어느 논쟁으로 공격받으면 밖으로 나간다.

The unique reinstatement labelling that corresponds to the system ${\displaystyle S}$ above is ${\displaystyle L=\{(a,{\mathit {in}}),(b,{\mathit {out}}),(c,{\mathit {out}}),(d,{\mathit {in}})\}}$.

주장 체계로부터의 추론

특정 의미론 $\sigma {\displaystyle }$ ${\displaystyle \sigma }$에 대해 여러 확장자를 계산한 일반적인 경우$,$ 시스템에서 원인을 찾는 에이전트는 다음과 같은 여러 메커니즘을 사용하여 정보를 추론할 수 있다.^[6]

• 믿을 수 있는 추론: $에이전트$가 {$${\$displaystyle \sigma$} -확장$$ 중 적어도 하나에 속할 경우 인수를 수락함. 이 경우 에이전트는 함께 허용되지 않는 일부 인수$({\displaystyle a}$ 공격 $b$ ${\displaystyle b}$및 ${\displaystystyle a$$}$ $및{\displaystyle }$ b$$$})$를 수락할 위험이 있음$$ 각각 확장자에 속함)
• 회의적인 추론: 에이전트는 모든 $\sigma {\displaystyle }$ ${\displaystyle \sigma}$ -extension에$$ 속하는 경우에만 주장을 받아들인다. 이 경우 대리인은 너무 적은 정보(연장의 교차점이 비어 있거나 매우 작은 추기경이 있는 경우)를 추론할 위험이 있다.

For these two methods to infer information, one can identify the set of accepted arguments, respectively ${\displaystyle Cr_{\sigma }(S)}$ the set of the arguments credulously accepted under the semantic ${\displaystyle \sigma }$, and ${\displaystyle Sc_{\sigma }(S)}$ the set of arguments accepted 의미론적 $\sigma {\displaystyle }$ ${\displaystyle \sigma}$에서 회의적으로(의미적으로 의미론적 모호성이 없을 경우 $\sigma {\displaystyle }${\$displaystyle \mama }$을(를) 놓칠$$ 수 있다.$$

물론 확장자가 하나만 있을 때(예를 들어, 시스템이 잘 구축되어 있을 때) 이 문제는 매우 간단하다: 대리인은 고유한 확장자의 주장을 받아들이고 다른 것을 거부한다.

그 같은 추론은 선택한 의미에 해당한다 labellings:각 성분 표시제에 있는 주장과 그래각 성분 표시제에 하면 다른 미결정의 상태에(주장의 상태 beliefs[7]의 역학에 대한 공대지 유도탄 체계에 대한 믿음의 인식론적 국가들 기억 나세요 거절했다 받아들여질 수 있는 할 수 있다.cm이다.

주장 프레임워크 사이의 동등성

주장 프레임워크 사이에는 몇 가지 동등성 기준이 존재한다. 그러한 기준의 대부분은 확장 또는 허용되는 인수 집합과 관련이 있다. 공식적으로 의미론적 $\sigma {\displaystyle }$ ${\displaystyle \sigma }:$

• ${\displaystyle {\mathit {EQ_{1}}}}$ : two argumentation frameworks are equivalent if they have the same set of ${\displaystyle \sigma }$-extensions, that is ${\displaystyle S_{1}\equiv _{1}S_{2}\Leftrightarrow Ext_{\sigma }(S_{1})=$$Ext_{\sigma }(S_{2})$ $$;
• ${\displaystyle {\mathit {EQ_{2}}}}$ : two argumentation frameworks are equivalent if they accept skeptically the same arguments, that is ${\displaystyle S_{1}\equiv _{2}S_{2}\Leftrightarrow Sc_{\sigma }(S_{1})=Sc_{\sigma }(S_{2})}$ ;
• ${\displaystyle {\mathit {EQ_{2}}}}$ : two argumentation frameworks are equivalent if they accept credulously the same arguments, that is ${\displaystyle S_{1}\equiv _{3}S_{2}\Leftrightarrow Cr_{\sigma }(S_{1})=Cr_{\sigma }(S_{2})}$.

강한 equivalence[8]S3{\displaystyle S_{3}과 함께 두 시스템 S1{\displaystyle S_{1}}과 S2{\displaystyle S_{2}} 같다 다른 모든 시스템에 만일 S3{\displaystyle S_{3}}, S1의 노조{\displaystyle S_{1}}}은 등가( 주어진 척도인지를) 말한다. 재치h S ${\displaystyle {2\mathrm{}}_{}}$ ${\$}} 및$$ $S{\displaystyle {}_{}}$ ${\displaystyle {3\mathrm{}}_{}}$ ${\$의 조합$.$^[9]

기타종류

둥의 추상적인 틀은 몇 가지 특정한 사례로 인스턴스화되었다.

논리 기반 주장 프레임워크

논리 기반의 주장 프레임워크의 경우, 논쟁은 추상적인 실체가 아니라 한 쌍으로, 여기서 제1부는 논쟁의 제2부에 대한 공식을 증명할 수 있을 정도로 최소한의 일관적인 공식 집합이다. 형식적으로 인수는 다음과 같은$$ 쌍$({\displaystyle }$ ${\displaystyle \mathrm{\phi }}$ ,${\displaystyle \alpha }$) ${\displaystyle (\Phi ,\alpha )}$이다.

• $Phi \nvdash \bot }$
• $\displaystyle \Phi \vdash \alpha }$
• ${\displaystyle \mathrm{\phi }}$ ${\displaystyle \Phi }$은(는) $\alpha {\displaystyle }$ ${\displaystyle \Delta$$$$}$을(를) 만족하는 최소 ${\displaystyle$ \Delta }의 집합이며, 여기서$$ $\Delta {\displaystyle \mathrm{}}${\$displaystyle \Delta}$은 에이전트에서 사용하는 공식 집합이다.

$\alpha {\displaystyle \mathrm{}}$ ${\displaystyle$ $\$$alpha}$의 결과물인$$α {\$displaystyle$ \$Phi$$}$과$($$와{\displaystyle \mathrm{}}$) $\$ {\$displaystyle$ \alpha$$$}$의 $지원$을 α$${\$displaystyle \alpha$ }이라고 부른다$.$

이 경우 공격 관계는 카르테시안 $제품$ $A$${\displaystyle \times }$ $A$의 하위 집합으로서 명시적인 방법으로 주어지는 것이 아니라, 인수가 다른 것을 공격하는지 여부를 나타내는 속성으로서 주어진다$.$ 예를 들어.

• Relation defeater : ${\displaystyle (\Psi ,\beta )}$ attacks ${\displaystyle (\Phi ,\alpha )}$ if and only if ${\displaystyle \beta \vdash \neg (\phi _{1}\wedge \dots \wedge \phi _{n})}$ for ${\displaystyle \{\phi _{1},\dots ,\phi _{n}\}\subsete$$\Phi }$
• Relation undercut : ${\displaystyle (\Psi ,\beta )}$ attacks ${\displaystyle (\Phi ,\alpha )}$ if and only if ${\displaystyle \beta =\neg (\phi _{1}\wedge \dots \wedge \phi _{n})}$ for ${\displaystyle \{\phi _{1},\dots ,\phi _{n}\}\subseteq \Phi$$}$
• 관계 반박 : (${\displaystyle \mathrm{\psi }}$ ,${\displaystyle \beta }$) ${\displaystyle (\PSi ,\beta )}$공격$$ ($$ ,$$) {\$displaystyle (\Phi$ ,\alpha $)}$ 만약$$ $\beta {\displaystyle }$ ${\displaystyle \iff }$ β $displaystyle \beta \neg \nepha }$인 경우에만 해당된다.

특정한 공격 관계를 고려할 때, 추상적인 주장 프레임워크와 유사한 방법으로 그래프와 이유를 구축할 수 있다(확장, 회의적 또는 신뢰적 추론을 구축하기 위한 의미론적 사용), 차이점은 논리에 근거한 주장 프레임워크에서 추론된 정보가 공식의 집합(허용된 논쟁의 결과)이라는 것이다.움푹 패다

가치 기반 주장 프레임워크

가치 기반 주장 프레임워크는 논쟁의 교환 동안, 어떤 것들은 그들이 전진하는 어떤 가치에 관해서 다른 것들보다 더 강해질 수 있고, 따라서 논쟁들 사이의 공격의 성공은 이러한 가치들의 차이에 달려있다.

Formally, a value-based argumentation framework is a tuple ${\displaystyle VAF=\langle A,R,V,{\textit {val}},{\textit {valprefs}}\rangle }$ with ${\displaystyle A}$ and ${\displaystyle R}$ similar to the standard framework (a set of arguments and a binary relation on this set), $$${\displaystyle V}$ ${\displaystyle V}$은(는) 비어 있지 않은 값 집합이고, ${\displaystyle \mathit{\text{val}}}$ ${\${$val$$}$은(는) $A{\displaystyle }$ ${\displaystyle A}$의 각 요소를 V ${\displaystystyle V}$의 요소와$$ 연결하는 매핑이며$,$ ${\displaystyle \mathit{\text{valprefs}}}$ ${\$type{\$data$.ic) $V{\displaystyle }$ ${\displaystyle \times }$ ${\displaystyle V}$ ${\displaystyle V\time$ V$}$에 표시$.$

$이{\displaystyle }$ 프레임워크에서 ${\displaystyle a}$ 인수는 다음인 경우에만$$ 다른 $인수{\displaystyle }$ b ${\displaystyle b}$을(를) 패배시킨다.

• ${\displaystyle a}$"표준$"$의 "${\displaystyle b}$$"$ 공격$$$$ b {\$displaystyle b}:$ (${\displaystyle }$, b${\displaystyle }$) ${\displaystyle \in }$ ${\displaystyle R}$ ${\displaystyle (a,b)\in$ R$};$
• $및{\displaystyle }$${\displaystyle }$(${\displaystyle \mathit{\text{val}}}$(${\displaystyle b}$)${\displaystyle }$, ${\displaystyle v}$ ${\displaystyle a}$(${\displaystyle }$)${\displaystyle \notin }$ ${\displaystyle \mathit{\text{valprefs}}}$ ${\$),$val($a)\$not \$in {\$textit$ {$valprefs$$$이 값은 {\$displaystyle a}$에 의해 진전된 값보다 선호되지 않는다$$$.$

두 주장이 동일한 값에 연관되어 있거나 각각의 값 사이에 선호도가 없는 경우 공격이 성공한다는 한 가지 언급.

가정 기반 주장 프레임워크

가정 기반 인수(ABA) 프레임워크에서 인수는 규칙 집합으로 정의되고 공격은 가정과 반론적 관점에서 정의된다.

형식적으로 가정 기반 논거 프레임워크는 튜플 ${\displaystyle ,}$ ${\displaystyle L\mathcal{}}$ ,${\displaystyle R\mathcal{}}$ ,${\displaystyle A\mathcal{}}$ ,${\displaystyle \stackrel{}{}}$¯ ${\displaystyle \stackrel{}{⟩}}$ ${\displaystyle \{}$ { { \ $\langle \mathcal {L},{\mathcal {R},{\mathcal {A},{\mathrm${\$textvisible}}}}},$ 여기서$$^[10][11][12]where$?$

• ${\displaystyle \langle {\mathcal {L}},{\mathcal {R}}\rangle }$ is a deductive system, where ${\displaystyle {\mathcal {L}}}$ is the language and ${\displaystyle {\mathcal {R}}}$ is the set of inference rules in the form of ${\displaystyle s_{0}\leftarrow s_{1},\d$$Otsc ,s_{m$$\},$ > 0 ${\displaystyle m>0}$ 및 s ${\displaystyle {0\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$,${\displaystyle {}_{}\dots ,}$ ${\displaystyle {}_{}}$m${\displaystyle {}_{}{m}_{}}$ ${\displaystyle L\mathcal{}}$ ${\$ {$L};$
• ${\displaystyle }$${\displaystyle A\mathcal{}}$ ${\$ 여기서 $A{\displaystyle \mathcal{}}$ ${\displaystyle \subseteq }$ L ${\$ {$A}\mathseteq {\mathcal {L}}$은(는) 비어 있지 않은 집합이며, 가정 이름:
• $␣}{\${\$mathrm {\textvisiblespace}}}}}$은(는) A$${\$displaystyle {\mathcal {A}$에서 $L{\displaystyle \mathcal{}}$ ${\$ ${\mathcal$${L}}($으)로의 총 매핑이며$,$ $여기$서$${\$displaystystylease}$은 {\displaysty$\}.$

ABA를 정의한 결과, 인수는 트리 형식으로 나타낼 수 있다.^[10] 형식적으로, 연역적 시스템과 가정의 집합 A⊆ 나는{\displaystyle{{A\mathcal}}\subseteq{{나는\mathcal}}}, 보상 청구 c의{\textstyle c\in{{나는\mathcal}∈ argument[10]}}S에 의한{\displaystyle S\sub ⊆ 지원되는⟨ L, R({\displaystyle \langle{{나는\mathcal}},{{R\mathcal}}\rangle}을 주어집니다.세트$eq {\mathcal{A}}$은$($는) $L{\displaystyle \mathcal{}}$ ${\$의 문장 또는$$ 기호 $\tau {\displaystyle }$ ${\displaystyle \tau$으)로 라벨을 표시한 노드가 있는 트리로서 다음과 같다.

• $루트{\displaystyle }$ 레이블은 c ${\displaystyle c}$
• $각{\displaystyle }$ 노드 N ${\displaystyle N}$에 대해$,$
  • $N{\displaystyle }$ ${\displaystyle N}$이(가) 리프 노드인 경우 $N{\displaystyle }$ ${\displaystyle N}$은(는) 가정 또는 $or{\displaystyle }$ ${\displaystyle \tau }$에 의해 레이블이 지정됨$$
  • If ${\displaystyle N}$ is not a leaf node, then there is an inference rule ${\displaystyle l_{N}\leftarrow s_{1},...,s_{m}}$, ${\displaystyle (m\geq 0)}$, where ${\displaystyle l_{N}}$is the label of ${\displaystyle N}$ and
    • $m{\displaystyle }$= ${\displaystyle 0}$ ${\displaystyle m=0$인 경우 규칙은 l ${\displaystyle N_{}}$ ${\displaystyle {}_{}}$ τ ${\displaystyle \tau }$ ${\displaystyle l_{N}\$좌측 $화살표 \tau$}이어야 한다($$$예{\displaystyle }$: N ${\\displaystyle N$}의 하위 항목은$$ $\tau {\displaystyle }${\$displaystystyle \tau$
    • 그렇지 않으면 $N{\displaystyle }$ ${\displaystyle$ N$}$에 s ${\displaystyle {1\mathrm{}}_{}}$,${\displaystyle }$. .${\displaystyle }$. .${\displaystyle {}_{}}$ ${\displaystyle m_{}}$ ${\$}, $...,s_{m}$로 레이블이 $지정$된 m ${\displaystyle m}$자녀가$$ 있음$$
• ${\displaystyle S}$ ${\displaystyle S}$은(는) 출발 노드에 레이블을 붙인 모든 가정의 집합이다.

일련의 가정 $S{\displaystyle }$ ${\displaystyle S}$이(가) 지원하는$$ $클레임{\displaystyle }$c {\$displaystyle$ $c$$}$이(가) 있는 인수는^[10] ${\displaystyle S}${$$c {\$displaysty$S\$vdash$ c$}$로도 나타낼$$ 수 있다.

참고 항목

메모들

참조