밸런스 퍼즐

이 글은 검증을 위해 추가 인용문이 필요합니다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선하는 데 도움을 주십시오. 조달되지 않은 자재는 제거될 수 있습니다.출처 : '밸런스 퍼즐'– 뉴스 · 신문 · 서적 · 학자 · JSTOR (2014년 1월) (템플릿 메시지 삭제 방법 및 삭제 시기 확인)

밸런스 퍼즐 또는 계량 퍼즐은 제한된 횟수만큼 밸런스 눈금을 사용하여 아이템(종종 동전)의 균형을 맞추는 논리 퍼즐입니다.이러한 항목은 가중치를 할당하는 퍼즐과는 다른데, 이러한 항목의 상대적 질량만 관련이 있다는 점이다.

알려진.	목표	n개의 무게에 대한 최대 동전	c 코인의 무게 측정 횟수
타겟 코인이 다른 코인보다 가볍거나 무거운지 여부	코인의 식별	${\displaystyle 3^{n}}$	$\displaystyle \lceil \log _{3}(c)\rceil}$
대상 코인이 다른 코인과 다릅니다.	코인의 식별	${\displaystyle {3^{n}-1}{2}}$[1]	$\displaystyle \lceil \log _{3}(2c+1)\rceil}$
대상 코인이 다른 코인과 다르거나 모든 코인이 동일합니다.	고유 코인이 존재하는지, 더 가볍고 무거운지 확인	${\displaystyle {3^{n}-1}{2}}-1}$	$\displaystyle \lceil \log _{3}(2c+3)\rceil}$

예를 들어, 세 가지 무게(n = 3)에서 유사하지 않은 동전을 탐지하는 경우 분석할 수 있는 최대 동전 수는 다음과 같습니다.3³ - 1/2 = 13 。무게가 3개이고 동전이 13개일 경우 마지막 동전의 정체를 확인할 수 있는 것은 아니며(다른 동전보다 무겁거나 가벼운지) 단지 동전이 다르다는 점에 유의하십시오.일반적으로 무게 n의 경우 3 - 1/2 - 1 이하의 동전이 있으면ⁿ 동전의 정체를 확인할 수 있습니다.n = 3의 경우 12개의 동전 중 다른 동전의 정체를 알 수 있습니다.

9코인 문제

잘 알려진 예로는 동전(또는 공)이 9개까지 있는데, 동전(또는 공)은 다른 것들보다 무게가 가볍고 짝퉁(홀수 공)입니다.그 차이는 저울로 재는 것만으로 알 수 있지만, 동전 자체의 무게를 재는 것만으로 알 수 있습니다.어떻게 두 개의 무게만으로 위조지폐를 분리할 수 있을까?

솔루션

해결책을 찾기 위해서는 우선 가벼운 것을 하나의 무게로 찾을 수 있는 최대 아이템 수를 고려합니다.가능한 최대 수는 3개입니다.가벼운 것을 찾으려면 세 번째를 빼고 두 개의 동전을 비교해 보면 된다.만약 두 개의 동전의 무게가 같다면, 더 가벼운 동전은 저울에 있지 않은 동전 중 하나일 것이다.그렇지 않으면 잔액에 의해 가벼워진 것으로 표시됩니다.

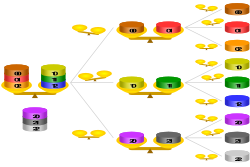
이제 각각 세 개의 동전이 세 개씩 쌓여 있는 아홉 개의 동전이 있다고 상상해 보세요.한 번에 세 개의 스택 중 어떤 스택이 더 가벼운지 확인할 수 있습니다(즉, 더 가벼운 코인이 들어 있는 스택).그런 다음 더 가벼운 더미 안에서 가벼운 동전을 식별하는 데 한 번만 더 움직이면 됩니다.따라서 두 개의 무게로 3 × 3 = 9의 세트에서 하나의 가벼운 동전을 찾을 수 있습니다.

더 나아가 27개의 동전 중에서 홀수 경동전을 찾는 데는 3개의 무게가 필요하고 81개의 동전 중에서 그것을 찾는 데는 4개의 무게가 필요할 것이다.

12코인 문제

더 복잡한 버전은 12개의 동전이 있는데, 그 중 11개 또는 12개가 동일하다.한쪽이 다르면 다른 쪽보다 무거운지 가벼운지 알 수 없습니다.이번에는 저울을 세 번 사용하여 독특한 동전이 있는지 여부를 판별할 수 있습니다.-만약 있다면, 동전을 분리하여 다른 동전에 대한 무게를 판별할 수 있습니다. (이 퍼즐과 해법은 1945년 기사에 처음 등장했습니다.)^[2]이 문제는 두 개의 저울에 세 개의 동전이 있는 단순한 변종과 네 개의 저울에 39개의 동전이 있는 더 복잡한 변종이 있다.

솔루션

이 문제에는 여러 가지 해결책이 있습니다.베이스 3의 번호를 사용하여 쉽게 더 많은 코인으로 확장할 수 있다: 베이스 3의 다른 숫자의 3자리 숫자로 각 코인에 라벨을 붙이고, 플레이트의 라벨과 동일한 n번째 숫자로 라벨이 표시된 모든 코인을 n번째 저울에 위치시킨다(스케일 양쪽에 각각 하나씩, sc에서 분리됨).ale) 기타 단계별 절차는 다음과 같다.이 문제는 간단하지 않으며, 두 번째와 세 번째 측정은 이전에 발생한 상황에 따라 달라집니다. 단, 반드시 그런 것은 아닙니다(아래 참조).

• 동전 4개가 양쪽에 놓여 있다.다음 두 가지 가능성이 있습니다.

1. 한쪽이 다른 쪽보다 무거워요.이 경우 무거운 쪽에서 동전 3개를 제거하고 가벼운 쪽에서 무거운 쪽으로 동전 3개를 옮긴 후 처음에는 무게가 실리지 않은 동전 3개를 가벼운 쪽에 놓습니다.(어떤 동전이 어떤 것인지 기억하십시오.)다음의 3가지 가능성이 있습니다.

1.a) 처음에 무거웠던 면은 여전히 무겁다.즉, 거기에 남아 있던 동전이 더 무겁거나 가벼운 쪽에 남아 있던 동전이 더 가볍다는 것을 의미합니다.이것들 중 하나를 다른 10개의 동전 중 하나와 균형을 맞추면 이것들 중 어느 것이 진실인지 밝혀내 퍼즐을 풀 수 있다.

1.b) 처음에 무거웠던 쪽이 두 번째로 가벼워진다.이것은 가벼운 쪽에서 무거운 쪽으로 넘어간 세 개의 동전 중 하나가 가벼운 동전이라는 것을 의미한다.세 번째 시도에서는 이 동전들 중 두 개를 서로 비교합니다. 한 개가 가벼우면 독특한 동전이고, 균형이 잡히면 세 번째 동전이 가벼운 동전입니다.

1.c) 양쪽이 짝수입니다.이것은 무거운 쪽에서 제거된 세 개의 동전 중 하나가 무거운 동전이라는 것을 의미한다.세 번째 시도에서는 이 동전들 중 두 개를 서로 비교합니다. 한 개가 무거우면 독특한 동전이고, 균형이 잡히면 세 번째 동전이 무거운 동전입니다.

2. 양쪽 다 똑같아.이 경우 8개의 동전은 모두 동일하며 적립할 수 있습니다.남은 동전 4개를 저울의 한쪽에 3개를 놓으세요.8개의 동일한 동전 중 3개를 다른 쪽에 놓아라.다음의 3가지 가능성이 있습니다.

2.a) 나머지 3개의 동전이 더 가볍습니다.이 경우 세 개의 동전 중 하나가 홀수 동전이고 더 가볍다는 것을 알 수 있습니다.저 동전 세 개 중 두 개를 꺼내서 서로 저울질하세요.저울이 기울어져 있다면, 더 가벼운 동전은 홀수 동전입니다.두 개의 동전이 균형을 이룬다면 세 번째 동전은 잔액에 없는 홀수 동전이 되어 가벼워집니다.

2.b) 나머지 3개의 동전이 더 무겁다.이 경우 세 개의 동전 중 하나가 홀수 동전이고 더 무겁다는 것을 알 수 있습니다.저 동전 세 개 중 두 개를 꺼내서 서로 저울질하세요.저울이 기울면 무거운 동전이 홀수 동전입니다.두 개의 동전이 균형을 이루면 세 번째 동전이 균형을 이루지 못하면 홀수 동전이 나오고 무거워진다.

2.c) 나머지 3개의 동전 잔액이 경우 남은 동전을 다른 11개의 동전 중 하나와 비교해 보면 더 무거운지 가벼운지 같은지 알 수 있습니다.

바리에이션

13개의 동전 중 1개가 나머지와 다른(질량) 것으로 알려진 13개의 동전 모집단을 고려할 때, 다음과 같이 저울과 3개의 테스트를 통해 어떤 동전인지 쉽게 판단할 수 있다.

1) 4개 코인으로 구성된 2개 그룹과 나머지 5개 코인으로 구성된 3개 그룹으로 구분한다.

2) 테스트 1, 4개의 코인으로 이루어진 두 그룹을 서로 테스트합니다.

a. 동전이 균형을 이룬 경우 홀수 동전은 인구 5에 속하며 테스트 2a로 진행합니다.

b. 홀수 동전은 8개 동전의 인구에 속하므로 12개 동전의 문제와 동일하게 진행됩니다.

3) 5개 코인의 그룹 중 2a, 3개 코인의 테스트와 8개 코인의 모집단 중 3개 코인의 테스트:

a. 3개의 동전이 균형을 이룬다면 홀수 동전은 2개의 동전의 나머지 인구에 포함된다.2개의 동전 중 하나를 다른 동전과 비교하여 테스트합니다. 균형이 잡히면 홀수 동전이 마지막 테스트되지 않은 동전이고, 균형이 잡히지 않으면 홀수 동전이 현재 테스트 동전입니다.

b. 3개의 동전이 균형을 이루지 못할 경우, 홀수 동전은 3개의 동전으로 구성된 이 인구에서 나온 것입니다.밸런스 스윙 방향에 주의한다(위쪽은 홀수 코인이 가볍다는 의미, 아래는 무겁다는 의미).3개의 동전 중 하나를 제거하고 다른 동전을 저울의 다른 쪽으로 옮깁니다(다른 모든 동전을 저울에서 제거).잔액이 줄어들면 홀수 동전은 제거된 동전이 됩니다.저울이 방향을 바꾸면 홀수 동전은 반대편으로 이동한 동전이 되고, 그렇지 않으면 홀수 동전은 제자리에 남아 있던 동전이 된다.

레퍼런스 코인 포함

참고할 수 있는 진짜 동전이 하나 있다면 의심 동전은 13개일 수 있습니다.1에서 13까지의 동전과 정품 동전의 번호 0에 번호를 매기고 다음 무게를 임의의 순서로 측정합니다.

• 0, 1, 4, 5, 6 대 7, 10, 11, 12, 13
• 0, 2, 4, 10, 11 대 5, 8, 9, 12, 13
• 0, 3, 8, 10, 12 대 6, 7, 9, 11, 13

저울이 한 번만 어긋나면, 1개의 무게로만 나타나는 1, 2, 3개의 동전 중 하나여야 한다.균형이 잡히지 않으면 모든 저울에 나타나는 10-13 동전 중 하나여야 한다.27개의 결과 각각에 대응하는 1개의 위조 동전을 선택하는 것은 항상 가능합니다(너무 무겁거나 너무 가벼운 13개의 동전은 26개의 가능성). 단, 모든 무게가 균형 잡힌 경우 위조 동전이 없습니다(또는 그 무게가 정확합니다).이 계량에서 동전 0과 13을 삭제하면 12코인 문제에 대한 하나의 일반적인 해결책이 됩니다.

두 개의 동전이 위조된 경우, 이 절차에서는 일반적으로 둘 다 고르지 않고 오히려 진짜 동전을 고릅니다.예를 들어 동전 1, 2가 모두 위조품일 경우 동전 4, 5 중 하나를 잘못 선택한다.

참조 코인 없음

이 퍼즐의 완만한 변형에서는 짝퉁 동전을 찾기만 하면 됩니다. 다른 것과 비교해서 그것의 무게를 알 수 없습니다.이 경우, 이전에 모든 코인의 무게를 측정했던 모든 용액을 한 개의 추가 코인을 처리하기 위해 적용할 수 있습니다.이 동전은 결코 저울에 올려져 있지 않지만, 모든 저울의 균형이 잡히면 위조 동전으로 선택된다.어느 시점에 저울에 올려져 위조 동전으로 선택되는 동전은 항상 다른 동전에 대해 가중치를 할당할 수 있기 때문에 더 잘 할 수 없다.

결과에 관계없이 동일한 동전 세트의 무게를 측정하는 방법은 다음 중 하나를 허용합니다.

1. (12개의 동전 A~L 중) 모두 무게가 동일한지 결론을 내리거나 홀수 동전을 찾아 더 가볍고 무거운지 판단한다.
2. (13개의 동전 A~M 중) 홀수 동전을 찾아 12/13 확률로 더 가볍거나 무거운지 확인합니다(나머지 1/13 확률의 경우, 단지 다르다는 것).

각 체중 측정의 세 가지 가능한 결과는 왼쪽이 가벼울 경우 "\", 오른쪽이 가벼울 경우 "/", 양쪽이 같은 체중을 가질 경우 "–"로 나타낼 수 있습니다.무게에 대한 기호는 순서대로 나열되어 있습니다.예를 들어, "/-"는 첫 번째와 두 번째 무게에서 오른쪽이 더 가볍고 세 번째 무게에서는 양쪽의 무게가 같다는 것을 의미합니다.3개의 체중을 측정하면 다음과³ 같은 3 = 27개의 결과가 나온다."––"를 제외하고, 집합은 오른쪽에 있는 각 집합이 "/"를 가지도록 분할되고, 왼쪽에 있는 집합은 "\"를 가지며, 그 반대도 마찬가지입니다.

/// \\\  \// /\\ /\/ \/\ //\ \\/  \/– /\– –\/ –/\ /–\ \–/  \\– //– –\\ –// \–\ /–/  /–– \–– –/– –\– ––/ ––\  –––

왼쪽의 동전 수가 오른쪽의 동전 수와 같아야 의미 있는 결과를 얻을 수 있기 때문에 첫 번째 행은 무시하고 각 열에 동일한 수의 "\"와 "/" 기호(각 4개)를 붙입니다.행에 라벨이 부착되어 있으며, 동전의 순서는 관련이 없습니다.

\// A light // B light \/ B light \// C light \/ D light \// D light -\/ E light - // F light \– F light \– G light - G light - \/\ H light - /// H - H - Light - /////H - Light - H - Light - H - Light - H - H - Light - Light - H - Light - Light - Light - Light - Light - Light - Light - Light - Light - Light - Light - Light - Light -r 더 무겁거나(13코인 케이스), 또는 모든 코인의 무게가 같다(12코인 케이스)

위의 결과 패턴을 사용하여 각 저울에 대한 코인의 구성을 결정할 수 있습니다. 예를 들어, 세트 "\/– D 라이트"는 첫 번째 저울에서 코인 D가 왼쪽에 있어야 하고(그 면이 가벼워지도록 하기 위해), 두 번째 저울에서는 오른쪽에 있어야 하며 세 번째 저울에서는 사용되지 않아야 합니다.

첫 번째 계량: 왼쪽: ADGI, 오른쪽: BCFJ 두 번째 계량: 왼쪽: BEGH, 오른쪽: ACDK 세 번째 계량: 왼쪽: CFHI, 오른쪽: ABEL

그런 다음 결과를 테이블에서 읽습니다.예를 들어, 처음 두 번째 무게에서 오른쪽이 더 가볍고 세 번째 무게에서 양쪽의 무게가 같은 경우, 대응하는 코드 "//- G heavy"는 동전 G가 홀수이고 다른 ^[3]동전보다 무겁다는 것을 암시한다.

일반화

이 문제의 일반화는 Chudnov에 ^[4]설명되어 있습니다.

$R{\displaystyle {\mathrm{}}^{}}$ n${\$$displaystyle$$$\$mathbb$${$R$}$ ^{n$$$}$ ${\$ n { displaystyle n$$} 、 [${\displaystyle {}^{}{\mathrm{}}^{}}$ 1 ,${\displaystyle }$e ${\displaystyle {\mathrm{}}^{}}$ $displaystyle$[ \ $mathrm${$e }$ ^ { $}$^ {2}$$} display$$${\displaystyle {\mathrm{}}^{}}$ ${\displaystyle {}^{}}$ display display display ${\displaystyle {\mathrm{}}^{}}$ $display$ \ mathrm 2 、 \ $mathrm 2$displaydisplay displaydisplaydisplaydisplaydisplaydisplaydisplay 。${\displaystyle {}^{}}$n$$, {\$displaystyle$$\mathbb {R}$^{n$}}$ 벡터$$${\displaystyle \mathrm{}}$ e ${\displaystyle =}$($e$1, $...,$ e n${\displaystyle {}_{}}$)$display R$ n \ $displaystyle \mathrm {e} =$( $e_{n})\in$ \$mathbb$${\displaystyle }$ {R}$^{n}$및 $하위$ 집합 E$=$ {$j$}${\displaystyle {}^{}}$$ystyle (\cdot )^{*}$ 및$displaystyle$ (\$cdot )^{+}}$는 각각 e ${\displaystyle =}$ ( ${\displaystyle s}$ ${\displaystyle i}$ ${\displaystyle g}$n ( ${\displaystyle {}_{}{i}_{}{}_{}}$) )${\displaystyle i_{}}$ ${$ $displaystyle \mathrm { e$ } ^{*} = ($sign$ ( $e$_ { $i$} )로 정의됩니다.$\_{\displaystyle {\mathrm{}}^{}}$${i}};$ $E{\displaystyle {}^{}}$ ${\displaystyle {\ast }^{}=}$ { (${\displaystyle {}^{}}$ ${\displaystyle {\mathrm{}}^{}}$ )${\displaystyle {}^{}}$∗ } $=$ \ { \ { \ { \ $mathrm { e }^{$ *$$} \ $\}$ ,${\displaystyle {}^{}}$$e{\displaystyle {}^{}}$ + ${\displaystyle =}$ ( ${\displaystyle \mathrm{si}}$ ${\displaystyle g}$n ( ${\displaystyle e_{}}$i${\displaystyle {}_{}}$)$$ \$display$ style \ mathrm { e } ^ { + = ( sign ( ${\displaystyle {\mathrm{}}^{}}$$_$ { i $)$ } ) ${\displaystyle {}^{}}$ { i } } ${\displaystyle 、}$ { i } } ${\displaystyle {}^{}<img\; alt="\{\backslash mathrm\; \{e\}\}^\{\{+\}\}=(|sign(e\_\{i\})|)\_\{i\}"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/c96ac58798ed1bb3c19723d6c5e2b9dbbac6f2d5"\; style="vertical-align:\; -0.838ex;\; width:17.64ex;\; height:3.009ex;">}$、 { $display$ sty$$} } 、 { $display sty$ }$}$ {\$displaystyle$ $I^{$n$$$\}$으로 R$n$의 이산 [-1; 1$]-$입방체, 즉 알파벳 I$=$ {${\displaystyle }$- ${\displaystyle 1}$,$0$, $1 }$의 $길이$n ${\$$displaystyle$n$$}의 모든 시퀀스 집합을 나타냅니다$.$t ${\displaystyle \}}$ ${\displaystyle \subseteq }$ ${\displaystyle I^{}}$ n$${ $style$ I _ { $t$}^$n$= \ { \ $mathrm { x } w$( \ $mathrm${$x$} ) \$leq$ t \ } \ $leceq$ I^ { $n$} 은$$ 반지름${\displaystyle }$t { $display$ $style{\displaystyle }$ t$$${\displaystyle \}<img\; alt="t"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/65658b7b223af9e1acc877d848888ecdb4466560"\; style="vertical-align:\; -0.338ex;\; width:0.84ex;\; height:2.009ex;">}$ (\$display style$${\displaystyle }$w$$)의 이산 볼입니다$.$cts는 벡터 $x{\displaystyle \mathrm{}}$ ${\displaystyle =}$ ( ${\displaystyle {}_{}{}_{}}$1${\displaystyle }$, ${\displaystyle ...}$ ,${\displaystyle {}_{}{x}_{}}$ n )$i$In $,$ \ $displaystyle$\$mathrm { x$} $=$ ( $x$_ {1} , \ display , $x$_ { $n$$}$ \ $in$ I$^$ { n } )에 의해 지정됩니다.${\displaystyle {이}_{}}$ 경우 i${\displaystyle {}_{}}$$${$displaystyle$$$i}번째${\displaystyle }$ 객체는 표준 가중치를 $가집니다.$$le$ i$}$${\displaystyle \mathrm{번째<img\; alt="i"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/add78d8608ad86e54951b8c8bd6c8d8416533d20"\; style="vertical-align:\; -0.338ex;\; width:0.802ex;\; height:2.176ex;">}}$ 개체는 x ${\displaystyle i_{}}$ $1$${\displaystyle (\mathrm{각각}}$$$x i = - 1(각각 $x{\displaystyle {}_{}}$ ${\displaystyle i_{}}$ $=$ - 1$(\display$ style $x_{i$}=-$1)$인 경우 상수(표준) 값만큼 커집니다.벡터${\displaystyle {\mathrm{}}^{}}$x$$+(\$displaystyle \mathrm {x}^{+})$는 오브젝트의 유형을 나타냅니다$$.표준 타입, 비표준 타입(타입의 설정)은 비표준 오브젝트의 상대적인 무게에 대한 정보는 포함되지 않습니다.

$중량{\displaystyle \mathrm{}}$(체크)은 벡터 h${\displaystyle \mathrm{}}$${\displaystyle {}^{}}$${\displaystyle I^{}}$n$$$;\$$displaystyle$$\mathrm {h}\$$in$ I$^{n}\$$in$ I$^{$n}\$in$ I^{$n}$s$$${\displaystyle (x\mathrm{}}$ ; h${\displaystyle )=}$ $($ ${\displaystyle h\mathrm{})}$이다.그 측량 벡터 h에 의해)(h1,…, hn){\displaystyle \mathrm{h}=(h_{1},\dots{n,h_})}:만약 내 0{\displaystyle h_{나는}\neq ≠ h0}일 경우 주어진 점검을 나는 머리에 th개체가 참여하{\displaystyle 나는}, 만약 내 h&이 왼쪽 균형 팬에 배치됩니다 다음과 같은 해석이 있다.그것은.0{\displaystyle h_{나는}<0}그리고 팬 만약 내입니다. h;0.{\displaystyle h_{나는}> 오른쪽에 배치됩니다;0.}의 스니커를 h{\displaystyle \mathrm{h} 들어}, 둘 다 프라이팬:어떤 팬에 개체의 수대로 되는 것보다 작은 것-경우에는, 몇몇 r(h)h;1 받는 개체의 같은 번호가 쓰여 있어야겠습니다. …, 1] $\displaystyle$ r$(\mathrm {h})=[\mathrm$ {$h}$ ;$1,\display,1]$ 참조 객체$$.${\displaystyle 가중치\mathrm{}}$ s${\displaystyle (}$${\displaystyle x\mathrm{}}$${\displaystyle }$;$$h ) { $displaystyle$$s$(\$mathrm$ ${$$} ;\mathrm$ ${$$h$$0$인 $경우{\displaystyle }$ 왼쪽 팬은$($;${\displaystyle h\mathrm{}}$${\displaystyle }$) ${\displaystyle =}$ $display 1$인 경우 오른쪽 팬보다 $우선합니다.$pan은 ${\displaystyle s\mathrm{}}$(${\displaystyle }$x ;${\displaystyle h\mathrm{}}$ ) $=$ 1.\$displaystyle s(\$mathrm {x} $;\mathrm$ {$h})=1$인 $경우{\displaystyle }$ 왼쪽보다 무겁습니다$.$} 개체$$ 그룹의 무게 분포에 대한 초기 정보의 불완전성은 개체 Z${\displaystyle {}^{}}$ $,$ \$displaystyle$ Z$\subseteq I^{$n$$}(일명 허용 상황 집합이라고도 함)의 집합으로,${\displaystyle }$z $display$Z \displaystyle$Z$ \$in$Z의$$ 요소는 다음과 같다$.$'허용 가능한 상황'이라고 하죠

각 $무게{\displaystyle \mathrm{}}$h$(\displaystyle \mathrm${h$})$는 $집합{\displaystyle {}^{}}$ ${\displaystyle I^{}}$ n$(\$ I$^{n})$을 평면$({\displaystyle }$x${\displaystyle }$;${\displaystyle h\mathrm{}}$) ${\displaystyle =}$${\displaystyle 0}$$(\displaystyle$[\$mathrm {x}$ ;\$mathrm {h})$으로 3부분$$ W${\displaystyle (S^{}}$In${\displaystyle h\mathrm{}}$ ;) ${\displaystyle =}$ {${\displaystyle {}^{}\}}$ )로 분할하도록 유도한다.$m {h}$ ${\displaystyle =}$\{\$mathrm {x}$ \$in$ I$^{n} s(\mathrm {x}$;\$mathrm {h$${\displaystyle \}}$ ) $=$$s$\}}, s${\$I, {$style s\$in I$$${\displaystyle ,\},}$ s$$${\displaystyle i}$ defines 、${\displaystyle \mathrm{defines}}$ defines defines defines defines defines defines defines${\displaystyle }$= W ( 0 Z, h )+W ( ${\displaystyle 1}$ ${\displaystyle Z,}$ ${\displaystyle H}$)의 대응하는 파티션을 정의합니다${\displaystyle .}$$displaystyle$$$$}$

정의 1.WA$($측정 알고리즘) $길이{\displaystyle \mathcal{}}$${\displaystyle }$m({$displaystyle$ m$})$의 ${{$displaystyle {$A$$})$은 시퀀스 A < , , , {$display$ { A} ${\displaystyle {}^{}}$ < \ $mathrm${ A$} =$ < $\ mathrm$ { A} , \ mathrm { A > 입니다. $여기$서${\displaystyle {}_{}}$A - ${\displaystyle 1^{}}$.$I^{j-1}\to$ I$^{n}$은 체크 ${\displaystyle {}^{}}$ j $=$ ${\displaystyle {}_{}}$j ( ${\displaystyle {}^j}$ - ${\displaystyle 1^{});}$ ${\displaystyle {}^{}}$ j${\displaystyle {}^{}{}^{}}$ $,$ \$displaystyle \mathrm {h}^{j$}=\$mathrm {A}_{j}(s^{j-1});\mathrm {h}^{n$}^{$n},$ {n$$}, n$},$ n}, n}, n}, n}, n, n, n, n, n, n, n, n, n, n, n, n, n, n, n, n, n, n,$s{\displaystyle {\mathrm{}}^{}}$${\displaystyle {}^{}}$j - ${\displaystyle 1^{}}$ ${\displaystyle =}$ ( ${\displaystyle {}_{}{}_{}{1\mathrm{}}_{}}$, ${\displaystyle ...}$ ,${\displaystyle {\mathrm{s}}_{}}$ j -${\displaystyle {}_{}{}_{}}$ )${\displaystyle i^{}}$ I${\displaystyle {\mathrm{j}}^{}}$- 1 ( $style$ \ $mathrm$${ s$ } ^ { j - 1 ） = ( s _ { s _ { 1} \ display , s$_$j - 1 )\ $in$ I^ { $j$ -$$$1 =$ ${\displaystyle {}_{}}$ （ s _ 1$）$ $。$

S${\displaystyle }$${\displaystyle }$(${\displaystyle Z}$ ,${\displaystyle A\mathcal{}}$) { $displaystyle$$$S ( Z , { \ $mathcal${ $A$} } } $all$( Z , A )$${ $displaystyle$ ( Z , { \ mathcal { A$$} ) } } ${\displaystyle \mathrm{s<img\; alt="(Z,\{\backslash mathcal\; \{A\}\})"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/b26495edef9fa695febc11b988fac81f1a17a04c"\; style="vertical-align:\; -0.838ex;\; width:6.427ex;\; height:2.843ex;">}}$ ${\displaystyle W\mathcal{}}$( s${\displaystyle }$)$$ I \ $displaystyle$W ( \$mathcal${ A ）$$i$$ of of of of $of of$ of of of of of of of of of of of of of of of of of of of of of of of of of of of of of of of of of of of of of of of of w w of of of of of of${\displaystyle I^{}}$${\displaystyle }$ m${\displaystyle s{}^{}}$ ( ${\displaystyle z\mathcal{}}$${\displaystyle }$A ) ${\displaystyle =}$ ${\displaystyle s}$ $=$ s ( \ $displaystyle$W ($s$ \ $mathcal${$$A$$} ) = \ $in$ I$^{m} s$ ($z$ \ $mathcal { A$${\displaystyle }$} =$$s \$\}$ ) ;${\displaystyle W}$ (${\displaystyle A}$) ${\displaystyle =W}$ .$display$ Z ; { \ cal \ $mathcal W$ ;$}$

정의 2.$WA$ A$(\$displaystyle ${A})$는 ${\displaystyle \mathrm{조건}}$ W$(s$ Z${\displaystyle ,}$ ${\displaystyle A)=}$ 1(\$displaystyle$ W$(s$ ${\displaystyle Z}$, {\$mathcal {A}) =1}$이(가) 모든${\displaystyle }$$$${\displaystyle }$S$;style$ S$)$에 대해 충족될 경우 설정된 Z(\$displaystyle Z)$의 상황을 식별한다고 합니다.${\displaystyle 조건{}^{}}$W${\displaystyle {}^{}}$+ (${\displaystyle s\mathcal{}}$ Z A${\displaystyle )}$ ${\displaystyle =}$ ${\displaystyle 1}${\$displaystyle$ W$^{+}(s$ Z${\mathcal {A}) =1$}이$($가) 모든 s ${\displaystyle †}$ $) .$ {\$displaystyle$ s$\in$ S$(Z{\$mathcal {$A}})$에 대해 충족될 경우 Z$(\displaystyle$ Z$)$에서 젝트가 표시됩니다.$}$

이른바 적절한 $세트$인$$Z(\$displaystyle$ Z$)$의 경우 유형이 Z$.\displaystyle$$Z$의 상황도 식별한다는 것이 입증되었습니다.$}$

예를 들어 $파라미터{\displaystyle }$ n ${\displaystyle =}$ ${\displaystyle 11,}$ ${\displaystyle m}$ ${\displaystyle =5}$, t ${\displaystyle =}$ ${\displaystyle 2}$ ${\displaystyle$ n$=11,m=5,t=2$}의$$ 완전한 다이내믹(2진법) 알고리즘은 완전한 3진법 Golay 코드(Virtakallio-Golay 코드)의 파라미터에 대응합니다.동시에 동일한 파라미터를 가진 정적 WA(가중치 코드)가 존재하지 않는 것이 확인된다.

각각의 알고리즘은 5개의 무게를 사용하여 11개의 동전 중에서 같은 값의 진짜 동전보다 무겁거나 가벼울 수 있는 최대 2개의 위조 동전을 찾아냅니다.이 경우 불확실성 영역(허용 가능한 상황 집합)은 1${\displaystyle }$+ ${\displaystyle 2}$ ${\displaystyle {}_{}^{}}$ ${\displaystyle {}_{}^{}}$1 + ${\displaystyle {\mathrm{}}^{}}$ ${\displaystyle {}^{}{}_{}^{}}$ ${\displaystyle {\mathrm{}}_{}^{}}$ 2 ${\displaystyle {}_{}^{}}$ ${\displaystyle {3\mathrm{}}^{}}$ 5$({$ 1$+2C_{11}^{1}+2^{2$})를 포함한다.$}C_{$$11$$}^{2}=3^{5$}}개의$$ 상황, 즉 생성된 WA는 t$=$ $2$ {\displaystyle$t=$2$$}에 대한 해밍 $경계$에 있으며, 이 점에서 완벽하다$.$

지금까지 것으로 알려지지 않는지 없는지 다른 완벽한 WA는 동일시한 상황에서 나는 하루에 500파운드 n{\displaystyle I_{t}^{n}}을 위한 값 n, 터{\displaystyle n,t}. 더구나, 그것은 알려진 어렵고 일부에선>2{\displaystyle t>2}이 존재한 해결을 위하여 방정식 ∑ 나는 갈0t2나는 Cni.) $(\$ _${i=0}^{t}2^{i}C_{n}^{i}=3^{m$})($$삼진코드용 해밍에 해당)는 완벽한 WA의 존재에 필수적입니다.t ${\displaystyle =}$ {$displaystyle$ t$=1$}의 경우 완벽한 WA가 존재하지 않으며 t ${\displaystyle =}$ {$displaystyle$ t$=2$}의 경우 이 방정식은 구성된 완벽한 WA의 매개변수를 결정하는 고유한 중요하지 않은 $솔루션{\displaystyle }$ n ${\displaystyle =}$ ${\displaystyle 11,}$ ${\displaystyle m}$ ${\displaystyle =}$ ${\displaystyle 5}$ {$displaystyle$ n=$11, m= 5}$을 갖는다는 사실만 알려져 있다.

오리지널 평행 계량 퍼즐

콘스탄틴 노프가 이 퍼즐을^{[citation needed]} 발명했다.구분이 안 되는 N개의 동전이 있는데, 그 중 하나는 가짜입니다(모두 같은 무게의 진짜 동전보다 무거운지 가벼운지는 알 수 없습니다).병렬로 사용할 수 있는 밸런스 척도는 두 가지가 있습니다.각각의 무게는 1분 동안 지속된다.5분 안에 ^[5]가짜 동전을 찾을 수 있는 가장 많은 동전 N은 몇 개입니까?

문학에서

• 피어스 앤서니의 소설 With a Langled Skin의 주인공인 니오베는 지옥에서 그녀의 아들을 찾기 위해 이 퍼즐의 12코인 변형을 풀어야 한다: 사탄은 아들을 다른 11명의 악마와 똑같이 보이게 위장했고, 그는 저주를 받느냐 아니면 진실하게 말할 수 있느냐에 따라 무거워지거나 가벼워진다.이 책의 솔루션은 주어진 예 1.c를 따릅니다.
• 줄리오 세사르 드 멜로 에 소자의 책 '세운 남자'의 주인공 베레미즈는 8개의 똑같은 모양의 진주(다른 진주보다 약간 가벼운 진주)를 가진 표준 균형 퍼즐을 들고 도전하는 인도 상인과 마주친다.베레미즈는 두 가지 가중치만 사용하여 문제의 모든 변수를 명시적으로 프레이밍함으로써 문제를 해결합니다.

텔레비전에서

• 사이버체이스의 웨딩스캐머에서 주인공들은 8개의 키(나머지 7개는 무게가 같다) 중 더 가벼운 키를 찾아 두 개로 충분할 때 3개의 무게로 차선책으로 해결한다.
• Columbo의 "The Bye-Bye Sky High IQ Murder Case" 에피소드에서 Columbo는 다음 퍼즐을 푼다: https://www.mathsisfun.com/puzzles/weighing-10-bags-solution.html
• Brooklyn Nine-Nine의 "Captain Peralta" 에피소드에서 홀트는 12명의 남자와 시소가 관련된 12개의 동전 문제에 대한 버전을 그의 팀에 제시한다.

레퍼런스

외부 링크

이 문서의 외부 링크 사용은 Wikipedia의 정책 또는 지침을 따르지 않을 수 있습니다. 과도한 외부 링크나 부적절한 외부 링크를 삭제하고 필요에 따라 유용한 링크를 각주 참조로 변환하여 이 문서를 개선하십시오.(2017년 8월) (이 템플릿메시지 삭제 방법 및 삭제 시기 확인)

• 첫 번째 퍼즐의 플레이 가능한 예
• 두 번째 퍼즐의 플레이 가능한 예
• 2판 잔액과 일반 위조지폐 문제
• Python으로 작성된 임의의 개수의 항목과 측정값에 대한 문제를 해결하는 소프트웨어