생일 공격

생일 공격은 확률론에서 생일 문제의 이면에 있는 수학을 악용하는 암호 공격의 일종이다. 이 공격은 둘 이상의 당사자 사이의 통신을 악용하는 데 이용될 수 있다. 공격은 무작위 공격 시도와 일정한 순열도(피건홀) 사이에서 발견되는 충돌의 높은 가능성에 따라 달라진다. 생일 공격의 경우 해시함수의 ${\textstyle {\sqrt {2^{n}}}=2^{n/2}}$ 을 ${\textstyle {\sqrt {2^{n}}}=2^{n/2}}$ = ${\textstyle {\sqrt {2^{n}}}=2^{n/2}}$ ${\textstyle {\sqrt {2^{n}}}=2^{n/2}}$ ${\textstyle {\sqrt {2^{n}}}=2^{n/2}}$ {\ $textstyle {2^{n}}=2^{n/2$ ${\textstyle 2^{n}}$ {\ $textstyle 2^{n}}}}$ 는 ${\textstyle 2^{n}}$ 고전적인 프리이미지 저항 보안이다. 양자 컴퓨터가 생일공격을 할 수 있어 충돌저항을 깨뜨릴 수 있다는 일반적(논의^[1]) 결과가 ${\textstyle {\sqrt[{3}]{2^{n}}}=2^{n/3}}$ ${\textstyle {\sqrt[{3}]{2^{n}}}=2^{n/3}}$ = ${\textstyle {\sqrt[{3}]{2^{n}}}=2^{n/3}}$ / 3 ${\$ 에 있다 ${\textstyle {\sqrt[{3}]{2^{n}}}=2^{n/3}}$ ^[2]

문제 이해

생일 문제 (1)과 생일 공격 (2)의 비교:

(1)에서 충돌은 한 세트 내에서 발견되는데, 이 경우 24개의 달 우주비행사가 276쌍 중 3쌍이 된다.

(2)에서는 두 세트 간에 충돌이 발견되는데, 이 경우 16개 변종 16개 변종 SHA-256 해시의 첫 바이트 256쌍 중 1쌍이 양성과 악의적인 계약으로 이루어진다.

예를 들어 30명의 학생(n = 30)을 가진 교사가 모든 사람의 생일을 묻는 시나리오(단순함을 위해 윤년은 무시)를 생각해 두 학생이 같은 생일을 가지는지(더 이상 설명한 해시 충돌에 대응)를 판단한다. 직관적으로, 이 기회는 작아 보일 수도 있다. 반직관적으로, 적어도 한 명의 학생이 어떤 날 다른 학생들과 생일이 같을 확률은 $1-{\frac {365!}{(365-n)!\cdot 365^{n}}}$ - $1-{\frac {365!}{(365-n)!\cdot 365^{n}}}$ ( $1-{\frac {365!}{(365-n)!\cdot 365^{n}}}$ - $1-{\frac {365!}{(365-n)!\cdot 365^{n}}}$ ) 공식으로부터 약 70%(n = 30)이다 $1-{\frac {365!}{(365-n)!\cdot 365^{n}}}$ $1-{\frac {365!}{(365-n)!\cdot 365^{n}}}$ $1-{\frac {365!}{(365-n)!\cdot 365^{n}}}$ n ${\$ !}{( $365-n!)!$ $\cdot 365^{n$ ^[3]

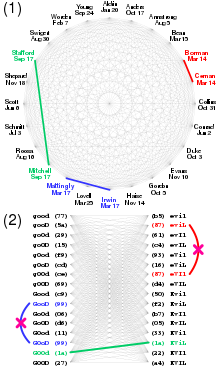
만약 선생님이 특정한 날(예: 9월 16일)을 선택했다면, 적어도 한 명의 학생이 그 특정한 날에 태어났을 확률은 $1-(364/365)^{30}$ - $1-(364/365)^{30}$ ( $1-(364/365)^{30}$ / $1-(364/365)^{30}$ ) $1-(364/365)^{30}$ $(\$ 약 7.9%이다.

생일 공격에서 공격자는 각각 디지털 서명이 있는 다양한 종류의 양성 및 악의적인 계약을 준비한다. 동일한 서명을 받은 양성 및 악의적인 계약 쌍을 구한다. 이 가상의 예에서 문자열의 디지털 서명이 해당 SHA-256 해시의 첫 번째 바이트라고 가정해 보십시오. 발견된 쌍은 녹색으로 표시되며, 양성 계약(파란색) 또는 악성 계약(빨간색) 쌍을 찾는 것은 무용지물이라는 점에 유의하십시오. 피해자가 양성 계약을 받아들인 뒤 공격자는 이를 악성 계약으로 대체해 피해자가 서명했다고 주장하는데, 이는 디지털 서명으로 입증된 것이다.

수학

Given a function $f$ , the goal of the attack is to find two different inputs $x_{1},x_{2}$ such that $f(x_{1})=f(x_{2})$ . Such a pair $x_{1},x_{2}$ is called a collision. 충돌을 찾는 데 사용되는 방법은 단순히 동일한 결과가 두 번 이상 발견될 때까지 무작위 또는 유사하게 선택할 수 있는 다른 입력 값에 대한 $f$ $f$ $f$ 함수를 평가하는 것이다. 생일 문제 때문에 이 방법은 효율적일 수 있다. 구체적으로는 $f(x)$ $f(x)$ x $f(x)$ ) {\ $displaystyle$ f $(x$ )}이 $f(x)$ (가 $)$ 동일한 확률로 H {\ $displaystyle H$ $}$ 개의 $H$ 다른 출력을 산출하고H {\ $displaystyle$ H}이(가) $충분히$ 큰 경우 $H$ , $f(x_{1})=f(x_{2})$ 가 포함된 $x_{2}$ 서로 다른 인수 $x_{1}$ $x_{1}$ $({\$ ${1}$ 및 ${2}}$ )를 얻을 것으로 예상한다. $f(x_{1})=f(x_{2})$ $f(x_{1})=f(x_{2})$ $f(x_{1})=f(x_{2})$ ) $f(x_{1})=f(x_{2})$ = $f(x_{1})=f(x_{2})$ ( $f(x_{1})=f(x_{2})$ $f(x_{1})=f(x_{2})$ ) ${\displaystyle f(x_{1})=f(x_{2$ })=f(x_{2 $})$ 는 $1.25{\sqrt {H}}$ 으로 1 $1.25{\sqrt {H}}$ ${\displaystyle$ 1 $.25{\sqrt{H}}$ 개의 서로 $1.25{\sqrt {H}}$ 다른 인수에 대해 함수를 평가한 $f(x_{1})=f(x_{2})$ 후 다음과 같이 하십시오.

우리는 다음과 같은 실험을 고려한다. H 값 집합에서 n 값을 무작위로 균일하게 선택하여 반복을 허용한다. p(n; H)를 이 실험 동안 적어도 하나의 값이 두 번 이상 선택될 확률로 두자. 이 확률은 다음과 같이 추정할 수 있다.

p(n;H)\약 1-e^{-n(n-1)/(2H)\약 1-e^{-n^{2}/(2H)}약 1-e^{-n^{2}/(2H)}}}}약 1-e^{-e^{n^{2}}}}}}}}}}}}

^[4]

n(p; H)은 우리가 선택해야 하는 최소값 수가 되도록 하여 충돌을 발견할 확률은 최소한 p가 되도록 한다. 위의 표현을 뒤집으면 다음과 같은 근사치를 찾을 수 있다.

n(p;H)\traft {\sqrt {2}H\ln {\frac {1}{1-p}}

그리고 우리가 도달한 충돌 확률 0.5를 할당한다.

[\displaystyle n(0.5)];H)\약 1.1774{\sqrt{H}}

Q(H)를 첫 번째 충돌을 찾기 전에 우리가 선택해야 하는 예상 값 수가 되도록 하자. 이 숫자는 다음과 같이 추정할 수 있다.

Q(H)\약간 {\sqrt {{\frac {\pi }{2}}:H}

예를 들어 64비트 해시를 사용할 경우 약 1.8×10개의¹⁹ 다른 출력이 있다. 만약 이 모든 것이 동일한 가능성(최상의 경우)이 있다면, 이 경우 약 50억 번의 시도(5.38×10⁹)가 있어야만 충돌할 수 있다.^[5] 이 값을 생일 바운드라고^[6] 하며, n비트 코드의 경우 대략 2로^n/2 추정할 수 있다.^[7] 그 밖의 예는 다음과 같다.

비트	가능한 출력(H)	원하는 무작위 충돌 확률 (2 s.f.) (p)
비트	가능한 출력(H)	10⁻¹⁸	10⁻¹⁵	10⁻¹²	10⁻⁹	10⁻⁶	0.1%	1%	25%	50%	75%
16	2¹⁶ (~6.5 x 10⁴)	<2	<2	<2	<2	<2	11	36	190	300	430
32	2³² (~4.3×10⁹)	<2	<2	<2	3	93	2900	9300	50,000	77,000	110,000
64	2⁶⁴ (~1.8×10¹⁹)	6	190	6100	190,000	6,100,000	1.9×10⁸	6.1×10⁸	3.3×10⁹	5.1×10⁹	7.2×10⁹
128	2¹²⁸ (~3.4×10³⁸)	2.6×10¹⁰	8.2×10¹¹	2.6×10¹³	8.2×10¹⁴	2.6×10¹⁶	8.3×10¹⁷	2.6×10¹⁸	1.4×10¹⁹	2.2×10¹⁹	3.1×10¹⁹
256	2²⁵⁶ (~1.2×10⁷⁷)	4.8×10²⁹	1.5×10³¹	4.8×10³²	1.5×10³⁴	4.8×10³⁵	1.5×10³⁷	4.8×10³⁷	2.6×10³⁸	4.0×10³⁸	5.7×10³⁸
384	2³⁸⁴ (~3.9×10¹¹⁵)	8.9×10⁴⁸	2.8×10⁵⁰	8.9×10⁵¹	2.8×10⁵³	8.9×10⁵⁴	2.8×10⁵⁶	8.9×10⁵⁶	4.8×10⁵⁷	7.4×10⁵⁷	1.0×10⁵⁸
512	2⁵¹² (~1.3×10¹⁵⁴)	1.6×10⁶⁸	5.2×10⁶⁹	1.6×10⁷¹	5.2×10⁷²	1.6×10⁷⁴	5.2×10⁷⁵	1.6×10⁷⁶	8.8×10⁷⁶	1.4×10⁷⁷	1.9×10⁷⁷

표에는 주어진 성공 확률을 달성하는 데 필요한 해시 수 n(p)가 표시되며, 모든 해시가 동등하다고 가정한다. 비교를 위해 10⁻¹⁸ ~ 10은⁻¹⁵ 일반 하드 디스크의 수정할 수 없는 비트 오류율이다.^[8] 이론적으로, 128비트인 MD5 해시 또는 UUID는 가능한 출력이 훨씬 더 많더라도 약 8,200억 개의 문서까지 그 범위 내에 있어야 한다.

기능의 출력이 고르지 않게 분포되어 있으면 충돌은 더욱 빨리 발견될 수 있다는 것을 쉽게 알 수 있다. 해시함수의 '균형' 개념은 생일 공격에 대한 함수의 저항을 계량화한다(불규칙한 키 분포를 설명). 그러나 해시함수의 균형을 결정하려면 일반적으로 가능한 모든 입력을 계산해야 하므로 MD 및 SHA 패밀리와 같은 인기 있는 해시함수의 경우 실행할 수 없다.^[9] $n(p;H)$ ( $n(p;H)$ ; $n(p;H)$ ) ${\displaystyle$ n(p; H) {\displaystyle n $(p;H)}$ 에 대한 방정식의 하위 $\ln {\frac {1}{1-p}}$ 표현 $\ln {\frac {1}{1-p}}$ - $\ln {\frac {1}{1-p}}$ ${\$ 은(는) 다음과 같이 공통 프로그래밍 언어로 직접 번역될 $p$ 때 $작은$ p ${\displaystystylease p}$ 에 대해 정확하게 계산되지 않는다 $n(p;H)$ . log(1/(1-p)) 의의 상실로 언제 log1p 사용 가능(예: C99에서 사용 가능) -log1p(-p) 대신 사용해야 한다.^[10] 이렇게 하지 않으면 위 표의 첫 번째 열은 0으로 계산되며, 두 번째 열의 여러 항목은 올바른 유의 자리 하나조차 갖지 못한다.

단순 근사치

정신적 계산에 사용될 수 있는 좋은 경험 법칙은 관계다.

2H}에 걸쳐 {\displaystyle p(n)\ 약 {n^{2} \}

라고도 쓸 수 있다.

H\approx {n^{2} \over 2p(n)}

H\approx {n^{2} \over 2p(n)}

H\approx {n^{2} \over 2p(n)}

H\approx {n^{2} \over 2p(n)}

H\approx {n^{2} \over 2p(n)}

H\approx {n^{2} \over 2p(n)}

( n

H\approx {n^{2} \over 2p(n)}

)

{\

또는

{\

H\time p(n

이것은 0.5 이하의 확률에 효과적이다.

이 근사도는 특히 지수를 사용할 때 사용하기 쉽다. 예를 들어 32비트 해시( $H=2^{32}$ = 2 $H=2^{32}$ ${\$ 를 제작하고 있으며 충돌 가능성이 100만분의 1( $p\approx 2^{-20}$ 2 $p\approx 2^{-20}$ - $p\approx 2^{-20}$ ${\$ 약 $2^{-20})$ 인 경우 최대 몇 개의 문서를 가질 수 있는가? $p\approx 2^{-20}$

n\sqrt {2\sqrt{32}\reason 2^{-20}={\sqrt{2^{1+32-20}}={\sqrt{2^{13}}}=2^{6.5}\ 약 90.5\

93이라는 정답에 가까운.

디지털 서명 취약성

디지털 서명은 생일 공격에 취약할 수 있다. 메시지 $m$ $m$ 은(는) 일반적으로 첫 번째 $f(m)$ f $f(m)$ ( m $f(m)$ ) $f(m)$ 에 의해 서명되며 $m$ $f(m)$ 여기서 $f$ $f$ 은(는) 암호 해시함수인 다음 $f$ , 어떤 비밀 키를 사용하여 $f(m)$ ( $f(m)$ ) ${\displaystystylease$ f $($ m $)$ 에 서명하도록 Bob을 속이고 싶다고 가정해보자 $f(m)$ 말로리는 공정한 계약 $m$ $m$ 과 $m$ 사기 $1m$ $'$ ${\$ 을(를) 준비한다 $m'$ 그런 다음 쉼표 삽입, 빈 줄 삽입, 문장 뒤에 1 대 2 공백, 동의어 교체 등 의미 변경 없이 $m$ ${\displaystym m}$ 을(를) 변경할 수 있는 $m$ 여러 위치를 찾는다. 이러한 변화를 결합함으로써 그녀는 모두 공정한 계약인 $m$ $m$ $m$ 에 엄청난 수의 변형을 만들 수 있다.

비슷한 방법으로 말로리는 또한 부정 $계약$ m{{\ $displaystyle$ m $'}$ 에 대해 엄청난 수의 변형을 만들어 낸다 $m'$ 그런 다음 $f(m)=f(m')$ 는 F $f(m)=f(m')$ ( m $f(m)=f(m')$ ) $f(m)=f(m')$ = $f(m)=f(m')$ ( $f(m)=f(m')$ $f(m)=f(m')$ ) ${\sty$ }을(를) 가진 부정 계약서의 버전을 찾을 때까지 이 모든 변형에 해시 함수를 적용한다. $그녀$ 는 밥에게 서명할 수 있는 공정한 버전을 제시한다 $f(m)=f(m')$ 밥이 서명한 후 말로리는 서명을 받아 사기 계약서에 첨부한다. 그리고 이 서명은 밥이 사기 계약서에 서명했다는 것을 증명한다.

맬로리는 같은 해쉬를 가진 두 개의 공정하지 못한 계약서를 찾아도 아무 이득도 얻지 못하기 때문에 원래 생일 문제와는 확률은 약간 다르다. 말로리의 전략은 한 쌍의 공정과 한 쌍의 부정 계약을 만들어 내는 것이다. $생일$ 문제 방정식은 n $n$ 이 $n$ (가) 쌍의 수입니다. 말로리가 실제로 생성하는 해시의 수는 $2n$ $2n$ 이다 $2n$

이 공격을 피하기 위해 서명 계획에 사용되는 해시함수의 출력 길이를 충분히 크게 선택하여 생일 공격, 즉 일반적인 짐승 같은 공격을 방지하는 데 필요한 비트의 약 2배를 계산적으로 실행할 수 없게 할 수 있다.

더 큰 비트 길이를 사용하는 것 외에도 서명자(Bob)는 서명하기 전에 문서에 대해 다소 무작위적이고 부당한 변경을 하고, 자신이 직접 서명한 계약서의 사본을 보관함으로써 자신을 보호할 수 있기 때문에 적어도 법정에서 자신의 서명이 그 계약서뿐만 아니라 그 계약서와 일치한다는 것을 증명할 수 있다.

폴라드의 로그 rho 알고리즘은 이산 로그 계산을 위해 생일 공격을 사용하는 알고리즘의 예다.

참고 항목

메모들

^ Daniel J. Bernstein. "Cost analysis of hash collisions : Will quantum computers make SHARCS obsolete?" (PDF). Cr.yp.to. Retrieved 29 October 2017.
^ Brassard, Gilles; HØyer, Peter; Tapp, Alain (20 April 1998). LATIN'98: Theoretical Informatics. Lecture Notes in Computer Science. 1380. Springer, Berlin, Heidelberg. pp. 163–169. arXiv:quant-ph/9705002. doi:10.1007/BFb0054319. ISBN 978-3-540-64275-6. S2CID 118940551.
^ "Math Forum: Ask Dr. Math FAQ: The Birthday Problem". Mathforum.org. Retrieved 29 October 2017.
^ Gupta, Ganesh (2015). "What is Birthday attack??". doi:10.13140/2.1.4915.7443. Cite 저널은 필요로 한다. journal= (도움말)
^ Flajolet, Philippe; Odlyzko, Andrew M. (1990). Quisquater, Jean-Jacques; Vandewalle, Joos (eds.). "Random Mapping Statistics". Advances in Cryptology — EUROCRYPT '89. Lecture Notes in Computer Science. Berlin, Heidelberg: Springer. 434: 329–354. doi:10.1007/3-540-46885-4_34. ISBN 978-3-540-46885-1.
^ 상한 및 하한을 참조하십시오.
^ Jacques Patarin, Audrey Montreuil (2005). "Benes and Butterfly schemes revisited" (PostScript, PDF). Université de Versailles. Retrieved 2007-03-15. Cite 저널은 필요로 한다. journal= (도움말)
^ Gray, Jim; van Ingen, Catharine (25 January 2007). "Empirical Measurements of Disk Failure Rates and Error Rates". arXiv:cs/0701166.
^ "CiteSeerX". Archived from the original on 2008-02-23. Retrieved 2006-05-02.
^ "Compute log(1+x) accurately for small values of x". Mathworks.com. Retrieved 29 October 2017.

참조

미히르 벨라레, 코노 다다요시: 해시함수의 균형과 그것이 생일 공격에 미치는 영향. 유로크립트 2004: pp401-418
응용 암호학, 브루스 슈나이어의 2부작

외부 링크

RSA Security의 암호화 FAQ에서 "디지털 서명이란 무엇이며 인증이란 무엇인가?"
"생일 공격" X5 네트워크 암호화 FAQ

[1] Daniel J. Bernstein. "Cost analysis of hash collisions : Will quantum computers make SHARCS obsolete?" (PDF). Cr.yp.to. Retrieved 29 October 2017.

[2] Brassard, Gilles; HØyer, Peter; Tapp, Alain (20 April 1998). LATIN'98: Theoretical Informatics. Lecture Notes in Computer Science. 1380. Springer, Berlin, Heidelberg. pp. 163–169. arXiv:quant-ph/9705002. doi:10.1007/BFb0054319. ISBN 978-3-540-64275-6. S2CID 118940551.

[3] "Math Forum: Ask Dr. Math FAQ: The Birthday Problem". Mathforum.org. Retrieved 29 October 2017.

[4] Gupta, Ganesh (2015). "What is Birthday attack??". doi:10.13140/2.1.4915.7443. Cite 저널은 필요로 한다. journal= (도움말)

[5] Flajolet, Philippe; Odlyzko, Andrew M. (1990). Quisquater, Jean-Jacques; Vandewalle, Joos (eds.). "Random Mapping Statistics". Advances in Cryptology — EUROCRYPT '89. Lecture Notes in Computer Science. Berlin, Heidelberg: Springer. 434: 329–354. doi:10.1007/3-540-46885-4_34. ISBN 978-3-540-46885-1.

[6] 상한 및 하한을 참조하십시오.

[7] Jacques Patarin, Audrey Montreuil (2005). "Benes and Butterfly schemes revisited" (PostScript, PDF). Université de Versailles. Retrieved 2007-03-15. Cite 저널은 필요로 한다. journal= (도움말)

[8] Gray, Jim; van Ingen, Catharine (25 January 2007). "Empirical Measurements of Disk Failure Rates and Error Rates". arXiv:cs/0701166.

[9] "CiteSeerX". Archived from the original on 2008-02-23. Retrieved 2006-05-02.

[10] "Compute log(1+x) accurately for small values of x". Mathworks.com. Retrieved 29 October 2017.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

Search