비에룸 플롯

때로는 실렌 도표 또는 헤그 도표로도 알려져 있다.

Bjerrum 플롯(Niels Bjerrum)은 용액이 평형 상태일 때 ^[1]pH의 함수로서 용액에 포함된 여러 종의 폴리프로틱산 농도를 그래프로 나타낸 것이다. 농도에 의해 확장되는 많은 순서의 크기 때문에, 그것들은 일반적으로 로그 척도로 표시된다. 때로는 실제 농도보다 농도의 비율이 표시되기도 한다. 때때로 H와⁺ OH도⁻ 표시된다.

가장 흔히 탄산염 계통이 도표로 되어 있는데, 여기서 폴리프로산(diprotic acid)은 탄소산(diprotic acid)이며, 다른 종은 용해된 이산화탄소, 탄산, 중탄산, 탄산염, 탄산염이다. 산성 조건에서 지배적인 형태는 CO2이고
, 기초적인 (알칼린) 상태에서는 지배적인 형태는₃²⁻ CO이며, 그 사이에 지배적인 형태는 HCO이다₃⁻. 매 pH마다 탄산의 농도는 용해된 CO의₂ 농도에 비하여 무시할 수 있다고 가정하고, 따라서 Bjerrum 플롯에서 누락되는 경우가 많다. 이 플롯들은 용액 화학 및 자연수 화학에 매우 도움이 된다. 여기에 제시된 예에서 화석연료 연소에 의한 인공 CO
₂ 배출 입력에 의한 해수 pH 및 탄산염 분화의 반응을 예시한다.^[2]

규산, 붕산, 황산, 인산을 포함한 다른 폴리프로테산들에 대한 Bjerrum 플롯은 다른 일반적으로 사용되는 예들이다.^[1]

탄산염 시스템의 Bjerrum 플롯 방정식

이산화탄소, 탄산, 수소 이온, 중탄산염, 탄산염 등이 모두 물에 용해된 경우, 화학적 평형상태에서 이들의 평형농도는 종종 다음과 같이 가정한다.

${\displaystyle{\begin{정렬}[]\left[{\textrm{카이 트리아 오닐}}_{2}\right]_{\text{eq}}&={\frac{\left[{\textrm{H}}^{+}\right]_{\text{eq}}^{2}}{\left[{\textrm{H}}^{+}\right]_{\text{eq}}^ᆴ+K_ᆵ\left[{\textrm{H}}^{+}\right]_{\text{eq}}+K_{1}K_{2}}}{\textrm{파종성 혈관 내 응고 병증}},\\[3pt]\left[{\textrm{수평 통제 병}}_{3}^{-}\right]_{\text{eq}}및 \times, ={\frac{K_{1}\left[{년.textrm{H}}^{+}\right 해결 _{\text{eq}}}{\left[{\textrm{H}}^{+}\right]_{\text{eq}}^ᆱ+K_ᆲ\left[{\textrm{H}}^{+}\right]_{\text{eq}}+K_{1}K_{2}}};={\frac{K_{1}K_{2}}{\left[{\textrm{H}}^{+}\right]_{\text{eq}}^ᆻ+K_ᆼ\left[{\textrm{H}}^{+}\right]_{\text{eq}}+K_{1}K_{2}}}\tim{\textrm{파종성 혈관 내 응고 병증}},\\[3pt]\left[{\textrm{카이 트리아 오닐}}_{3}^{2}\right]_{\text{eq}}및 \times.에스{\textrm {DIC},\end{aigned}}$

는 어디 첨자 'eq의 denotes이 있음을 평형 농도, K1은 균형의 반응이 CO2+H2O⇌ 여기에+HCO3−(탄산의 첫번째 산해리 상수와 같은)K2은 균형의 반응에 대해 일정하다 일정하다 HCO3− ⇌ H++CO32−(탄산의 두번째 산해리 상수와 같은), 파종성 혈관 내 응고 병증 i.s(unchanging) 시스템 내 용해된 무기탄소의 총 농도, 즉 [CO2
] + [HCO₃⁻] + [CO₃²⁻]. K₁, K₂, DIC는 각각 mol/liter와 같은 농도의 단위를 가진다.

Bjerrum 플롯은 주어진 K₁, K₂, DIC에 대해 pH = -log₁₀[H⁺]_eq에 대해 이 세 가지 종을 그림으로 표시하기 위해 이 세 가지 방정식을 사용하여 얻는다. 이 방정식의 분수는 세 종의 상대적 비율을 제공하므로 DIC를 알 수 없거나 실제 농도가 중요하지 않은 경우 이 비율을 대신 표시할 수 있다.

이 세 방정식은 CO2와
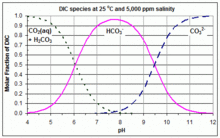
HCO의₃⁻ 곡선이 [H⁺]_eq = K에서₁ 교차하고, HCO와₃⁻ CO의₃²⁻ 곡선이 [H⁺]_eq = K에서₂ 교차한다는 것을 보여준다. 따라서 주어진 Bjerrum 그림을 만드는 데 사용된 K와₁ K의₂ 값은 이 교차점에서의 농도를 읽어냄으로써 그 그림에서 쉽게 찾을 수 있다. 선형 Y축의 예가 동봉된 그래프에 나와 있다. K와₁ K의₂ 값, 따라서 Bjerrum 그림의 곡선은 온도와 염도에 따라 크게 달라진다.^[3]

탄산염계 Bjerrum 플롯 방정식의 화학적 및 수학적 도출

모두 물에 용해된 이산화탄소, 수소 이온, 중탄산염, 탄산염 이온의 반응은 다음과 같다고 가정해 보자.

CO
₂⁺ + HO
₂ ⇌ H + HCO₃⁻(1)

HCO₃⁻⁺ ⇌ H + CO₃²⁻(2)

반응(1)은 실제로 다음과 같은 두 가지 기본적인 반응의 조합이라는 점에 유의하십시오.

CO
₂ + H
₂O ⇌ H
₂CO
₃ ⇌ H⁺ + HCO₃⁻.

이 두 반응에 대해 집단행동법이 적용된다고 가정하면, 물은 풍부하고, 다른 화학종들은 항상 잘 혼합되어 있다고 가정하면, 그들의 비율 방정식은 다음과 같다.

${\displaystyle{\begin{정렬}{\frac{{\textrm{d}}\left[{\textrm{카이 트리아 오닐}}_{2}\right]}{{\textrm{d}}t}}&=-k_ᆱ\left[{\textrm{카이 트리아 오닐}}_{2}\right]+k_ᆲ\left[{\textrm{H}}^{+}\right]\left[{\textrm{수평 통제 병}}_{3}^{-}\right],\\{\frac{{\textrm{d}}\left[{\textrm{H}}^{+}\right]}{{\textrm{d}}t}}&=k_ᆵ\left[{\textrm{카이 트리아 오닐}}_{2}\right]-k_{)}\left는 경우에는{\text.회사{H}}^{+}\right 해결 \left[{\textrm{수평 통제 병}}_{3}^{-}\right]+k_ᆰ\left[{\textrm{수평 통제 병}}_{3}^{-}\right]-k_ᆱ\left[{\textrm{H}}^{+}\right]\left[{\textrm{카이 트리아 오닐}}_{3}^{2}\right],\\{\frac{{\textrm{d}}\left[{\textrm{수평 통제 병}}_{3}^{-}\right]}{{\textrm{d}}t}}&=k_ᆴ\left[{\textrm{카이 트리아 오닐}}_{2}\right]-k_ᆵ\left[{\textrm{H}}^{+}\right]\left는 경우에는{\textrm{수평 통제 병}}_{3}^{-}\ri.ght]-k_{2}\left[{\textrm {HCO}}_{3}^{-}\right]+k_{-2}\left[{\textrm {H}}^{+}\right]\left[{\textrm {CO}}_{3}^{2-}\right],\\{\frac {{\textrm {d}}\left[{\textrm {CO}}_{3}^{2-}\right]}{{\textrm {d}}t}}&=k_{2}\left[{\textrm {HCO}}_{3}^{-}\right]-k_{-2}\left[{\textrm {H}}^{+}\right]\left[{\textrm {CO}}_{3}^{2-}\right],\end{aligned}}}$

여기서 [ ]은 농도를 나타내며 t는 시간이고₁ k와₋₁ k는 반응(1)에 대한 적절한 비례 상수로, 각각 이 반응에 대한 전진 및 후진 속도 상수로 불린다. (반응의 경우 k와₂ k와₋₂ 유사하게 (2))

어떤 평형에서든 농도는 변하지 않으므로 이 방정식의 왼손은 0이다. 그리고 이 네 방정식 중 첫 번째 방정식부터 반응 비율(1)의 비율 상수는 평형 농도의 비율과 같으며, K라고₁ 하는 이 비율을 반응에 대한 평형 상수, 즉 반응에 대한 평형 상수라고 한다.

${\displaystyle K_{1}={\frac {k_{1}}{k_{-1}}}={\frac {[{\textrm {H}}^{+}]_{\text{eq}}[{\textrm {HCO}}_{3}^{-}]_{\text{eq}}}{[{\textrm {CO}}_{2}]_{\text{eq}}}},}$ (3)

여기서 첨자 'eq'는 평형농도임을 나타낸다.

마찬가지로, 반응에 대한 평형 상수₂ K의 네 번째 방정식부터 (2)

${\displaystyle K_{2}={\frac {k_{2}}{k_{-2}}}={\frac {\left[{\textrm {H}}^{+}\right]_{\text{eq}}\left[{\textrm {CO}}_{3}^{2-}\right]_{\text{eq}}}{\left[{\textrm {HCO}}_{3}^{-}\right]_{\text{eq}}}}.}$ (4)

재배열 (3) 제공

${\displaystyle \left[{\textrm {HCO}}_{3}^{-}\right]_{\text{eq}}={\frac {K_{1}\left[{\textrm {CO}}_{2}\right]_{\text{eq}}}{\left[{\textrm {H}}^{+}\right]_{\text{eq}}}},}$ (5)

그리고 재배열(4)한 다음 (5)로 대체하면 다음과 같다.

${\displaystyle \left[{\textrm {CO}}_{3}^{2-}\right]_{\text{eq}}={\frac {K_{2}\left[{\textrm {HCO}}_{3}^{-}\right]_{\text{eq}}}{\left[{\textrm {H}}^{+}\right]_{$$\text{eq}}}={\frac$ {$K_{$1}$K_{$2}\$왼쪽[{\textrm$ {CO$}_{2}\오른쪽]{\textrm{eq}}}}{\textrm$ {{$H}^{+}\right]_{\eq}}}}}}}}($6)

시스템 내 용해된 무기탄소의 총 농도는 다음과 같다.

${\$$\&=\left[{\textrm {CO}}_{2}\right]_{\text{eq}}\left(1+{\frac {K_{1}}{\left[{\textrm {H}}^{+}\right]_{\text{eq}}}}+{\frac {K_{1}K_{2}}{\left[{\textrm {H}}^{+}\right]_{\text{eq}}^{2}}}\right)$$\\&=\left[{\textrm {CO}}_{2}\right]_{\text{eq}}\left({\frac {\left[{\textrm {H}}^{+}\right]_{\text{eq}}^{2}+K_{1}\left[{\textrm {H}}^{+}\right]_{\text{eq}}+K_{1}K_{2}}{\left[{\textrm {H}}^{+}\right]_{\text{eq}}^{2}}}\right).$$\$end{$aigned}}}을($를) (5) 및 (6)로 대체

이를
₂ 다시 설명하면 CO에 대한 방정식이 제공된다.

${\displaystyle \left[{\textrm {CO}}_{2}\right]_{\text{eq}}={\frac {\left[{\textrm {H}}^{+}\right]_{\text{eq}}^{2}}{\left[{\textrm {H}}^{+}\right]_{\text{eq}}^{2}+K_{1}\left[{\textrm {H}}^{+}\right]_{\text{eq}}+K_{1}K_{2}}}\times {\textrm {DIC}}.}$

HCO와₃⁻ CO에₃²⁻ 대한 방정식은 (5)와 (6)로 대체하여 구한다.

참고 항목

• 샬럿 방정식
• Gran 그림(Gran 적정법 또는 Gran 방법이라고도 함)
• 헨더슨-하셀발치 방정식
• 힐 방정식(생물화학)
• 이온정화
• 민물, 담수, 맑은 물
• 바닷물
• 테르모할린 순환

참조