국소 일관성
Local consistency제약조건 만족도에서 국소 일관성 조건은 변수나 제약조건의 하위 집합의 일관성과 관련된 제약조건 만족도 문제의 속성이다.검색 공간을 줄이고 문제를 쉽게 해결하는 데 사용할 수 있다.노드 일관성, 호 일관성, 경로 일관성 등 다양한 종류의 국소 일관성 조건이 활용된다.
모든 지역 일관성 조건은 해결책을 바꾸지 않고 문제를 바꾸는 변혁에 의해 시행될 수 있다.그러한 변환을 제약조건 전파라고 한다.제약조건 전파는 변수의 도메인을 축소하거나 제약조건을 강화하거나 새로운 도메인을 생성함으로써 작용한다.이는 검색 공간의 축소로 이어져 일부 알고리즘에 의해 문제를 쉽게 해결할 수 있다.제약 조건 전파는 일반적으로 불완전하지만 일부 특정한 경우에는 완전하지 않은 불만족 검사기로도 사용될 수 있다.
국소 일관성 조건은 다양한 등급으로 분류할 수 있다.원래 지역 일관성 조건은 모든 일관성 있는 할당을 다른 변수로 일관되게 확장할 수 있어야 한다.방향 일관성은 주어진 순서에 따라 다른 변수가 과제에서 변수보다 높을 때만 이 조건을 만족시키도록 요구한다.관계적 일관성에는 둘 이상의 변수에 대한 확장이 포함되지만, 이 확장은 주어진 제약조건이나 제약조건 집합을 충족시키기 위해서만 필요하다.
가정
이 글에서 제약조건 만족 문제는 변수 집합, 도메인 집합, 제약조건 집합으로 정의된다.변수와 도메인이 연관됨: 변수의 도메인은 변수에 취할 수 있는 모든 값을 포함한다.제약조건은 그 범위라고 불리는 일련의 변수와 제약조건을 만족시키는 평가인 일련의 평가로 구성된다.
이 글에서 언급된 제약 만족도 문제는 특별한 형태로 가정한다.모든 변수 순서가 최대 하나의 제약조건 또는 정확히 하나의 제약조건의 범위인 경우, 문제는 각각 정규형태로 정규화된 형태다.이항 구속조건에 대해서만 행해진 규칙성의 가정은 표준화된 형태로 이어진다.이러한 조건은 변수 시퀀스에 대한 모든 제약조건을 단일 제약조건으로 결합하거나 변수 시퀀스의 모든 값에 의해 충족되는 제약조건을 추가함으로써 항상 시행될 수 있다.
이 글에서 사용된 그림에서, 두 변수 사이의 연계가 없다는 것은 이 두 변수 사이에 어떤 제약조건이나 모든 값에 의해 충족되는 제약조건이 존재하지 않음을 나타낸다.[clarification needed]
국소 일관성
"표준" 지역 일관성 조건에서는 모든 일관된 부분 평가를 결과 할당 결과가 일관되도록 다른 변수로 확장할 수 있어야 한다.부분 평가는 범위가 할당된 변수의 부분 집합인 모든 제약조건을 만족하는 경우 일관된다.[clarification needed]
노드 일관성
노드 일관성을 위해서는 변수의 모든 단항 제약조건이 변수의 도메인의 모든 값에 의해 충족되어야 하며, 그 반대의 경우도 마찬가지다.이 조건은 각 변수의 도메인을 해당 변수에 대한 모든 단항 제약을 만족하는 값으로 감소시킴으로써 사소한 방법으로 시행될 수 있다.결과적으로, 단일 제약조건은 무시되고 도메인에 통합될 것으로 가정할 수 있다.
For example, given a variable with a domain of and a constraint , node consistency would restrict the domain to and the constraint could then be discarded. 이 전처리 단계는 이후의 단계를 단순화한다.
호 일관성
제약조건 만족도 문제의 각 허용 값이 두 번째 변수의 허용 가능 값과 일치하면 다른 변수와 원호 일관성이 있다.형식적으로 변수 x 은(는) x j {\ 와(와) 일치하며, 만약 x 의 도메인에 값 b}이(가가 있는 경우(, ) 이(가) i 와 사이의 이진 제약 조건을 만족한다는 것 모든 변수가 호와 일치하면 문제는 호와 일치한다.
예를 들어 변수가 도메인 1에서 3에 걸쳐 있는 제약 조건 < x을(를) 고려하십시오. 은(는) 절대 3이 될 수 없으므로 y 에는 3에서 값 사이의 호가 없으므로 제거해도 안전하다.마찬가지로 은(는) 절대 1이 될 수 없으므로 호가 없으므로 제거할 수 있다.
또한 호 일관성은 특정 이항 제약조건에 대해 정의될 수 있다. 한 변수의 모든 값이 제약을 만족하는 두 번째 변수의 값을 갖는 경우 이항 제약조건은 호 일관성이 있다.이러한 호 정합성의 정의는 위와 유사하지만 제약조건에 특정한 의미를 부여한다.위의 정의가 두 변수 사이의 모든 제약조건을 고려하는 반면 이 정의는 특정 변수만을 고려하는 비 정규화 문제에 특히 관련이 있다.
변수가 호와 다른 호가 일치하지 않을 경우, 해당 도메인에서 값을 제거하여 호를 만들 수 있다.이것은 호 일관성을 강제하는 제약조건 전파의 형태로서, 변수의 영역에서 다른 변수의 값에 해당하지 않는 모든 값을 제거한다.이 변환은 제거된 값이 어차피 해결책이 아니기 때문에 문제 해결 방법을 유지한다.
제약 조건 전파는 모든 변수 쌍에 대해 이 제거를 반복함으로써 전체 문제 호를 일치시킬 수 있다.이 프로세스는 주어진 변수 쌍을 두 번 이상 고려해야 할 수 있다.실제로 변수의 영역에서 값을 제거하면 다른 변수가 더 이상 변수와 일치하지 않을 수 있다.예를 들어, 3 가 2}}과 하지만 알고리즘이 x 2 {\2}}의 도메인을줄인다면 는 이상 유지되지 않으며, 다시 시행해야 한다.
단순 알고리즘은 변수 쌍에 걸쳐 순환하며, 아크 일관성을 적용하며, 전체 주기 동안 도메인이 변경되지 않을 때까지 주기를 반복한다.AC-3 알고리즘은 마지막으로 분석된 이후 수정되지 않은 제약조건을 무시함으로써 이 알고리즘에 걸쳐 개선된다.특히, 초기에 모든 제약조건을 포함하는 일련의 제약조건에 대해 작용한다. 각 단계에서 제약조건을 취하고 아크 일관성을 강제한다. 이 연산이 다른 제약조건에 대한 아크 일관성의 위반을 발생시킨 경우, 분석해야 할 제약조건 집합에 다시 배치한다.이러한 방식으로, 일단 제약조건에 대해 아크 정합성이 시행되면, 이 제약조건은 변수들 중 하나의 영역이 변경되지 않는 한 다시 고려되지 않는다.
경로 일관성
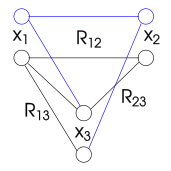
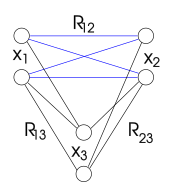
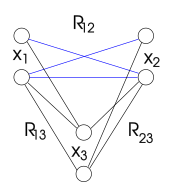
경로 일관성(path consistency)은 호 일관성(arc consistency)과 유사한 속성이지만 변수 쌍을 하나만 고려한다.변수 쌍은 모든 이항 제약 조건을 만족하는 방식으로 쌍에 대한 각 일관성 있는 평가를 다른 변수까지 확장할 수 있는 경우 세 번째 변수와 경로 일관성이 있다.형식적으로 및 는 x x_와 x {\ 사이의 이진 제약조건을 만족하는 값쌍에 대해 k x x k {\daysty x {{{nowsty과 일치한다.에 의 도메인에 값 이( 존재하며, 이러한 값은 ) 와 x 의 제약조건을 충족한다.및 k }} 각각
경로 일관성을 강제하는 제약조건 전파의 형태는 제약조건에서 일부 만족스러운 할당을 제거함으로써 작동한다.실제로 경로 일관성은 다른 변수로 확장할 수 없는 모든 평가를 이진 제약조건에서 제거하여 시행할 수 있다.호 일관성의 경우, 이 제거는 이항 구속조건을 두 번 이상 고려해야 할 수 있다.호 일관성에 대해서는, 제거된 값이 해결책이 없는 것처럼, 결과적인 문제는 원래의 것과 같은 해결책을 가지고 있다.
경로 일관성을 강제하는 제약조건 전파의 형태는 새로운 제약조건을 도입할 수 있다.두 변수가 이항 제약조건에 의해 관련되지 않는 경우, 두 변수는 어떤 값 쌍도 허용하는 제약조건에 의해 사실상 관련된다.그러나 일부 값 쌍은 제약 조건 전파에 의해 제거될 수 있다.결과 제약조건은 더 이상 모든 값 쌍에 의해 충족되지 않는다.그러므로 그것은 더 이상 가상적이고 사소한 제약이 아니다.
"경로 일관성"이라는 이름은 쌍과 단일 변수가 아닌 변수 쌍과 변수 사이의 경로를 포함하는 원래 정의에서 유래되었다.두 정의는 한 쌍의 변수에 대해 서로 다르지만 전체 문제를 언급할 때 동일하다.
일반화
호와 경로 일관성은 단일 변수 또는 쌍 대신 변수의 튜플을 사용하여 비이항 구속조건으로 일반화할 수 있다. - 변수의 튜플은 일관성을 유지하면서 - 1 변수에 대한 모든 일관성 있는 평가를 다른 변수의 값으로 확장할 수 있는 다른 변수와 일치한다.이 정의는 명백한 방법으로 전체 문제에까지 확장된다.strong -consistency는 j - 모든 j j
2-일관성의 특별한 경우는 호 일관성(모든 문제는 본 문서에서 노드 정합성이 있다고 가정함)과 일치한다.반면에, 3-정합성은 모든 제약조건이 이항인 경우에만 경로 일관성과 일치하는데, 경로 일관성은 3-정합성이 그러하지만 3-정합성은 3차 제약을 수반하지 않기 때문이다.
호 일관성을 일반화하는 또 다른 방법은 하이퍼 아크 정합성 또는 일반화된 호 정합성으로, 제약 조건을 충족하기 위해 단일 변수의 확장성을 필요로 한다.즉, 제약조건이 충족되는 방식으로 변수의 모든 값을 제약조건의 다른 변수까지 확장할 수 있는 경우 변수는 제약조건과 일치하는 하이퍼 아크(hyper-arc)이다.
일관성 및 만족도
제약 조건 전파(로컬 정합성의 형태를 강요)는 빈 도메인을 생성하거나 불만족스러운 제약 조건을 생성할 수 있다.이 경우 문제는 해결책이 없다.반대는 일반적으로 사실이 아니다: 일관되지 않은 예는 빈 영역이나 불만족스러운 제약이 없는 동안 호 일관성이 있거나 경로 일관성이 있을 수 있다.
사실, 국소 일관성은 변수 그룹의 일관성과만 관련이 있다.예를 들어, 호 일관성은 변수에 대한 모든 일관된 평가가 다른 변수에 일관되게 확장될 수 있음을 보장한다.그러나 변수의 단일 값이 다른 두 변수로 확장되면 이 두 값이 서로 일치한다는 보장이 없다.예를 들어, 1 = }은(는) x = {\} 및 = {\}과와) 일치할 수 있지만 이 두 평가는 서로 일치하지 않을 수 있다.
그러나 제약 조건 전파는 어떤 경우에는 만족도를 입증하는 데 사용될 수 있다.호 일관성이 있고 빈 도메인이 없는 이진 제약조건 집합은 제약조건의 네트워크가 주기를 포함하는 경우에만 일관성이 없을 수 있다.실제로 제약조건이 이항이고 반복 그래프를 형성하는 경우, 값은 항상 제약조건에 걸쳐 전파될 수 있다. 변수의 모든 값에 대해 제약조건이 있는 모든 변수에는 그러한 제약조건을 만족하는 값이 있다.결과적으로, 지정되지 않은 변수를 반복적으로 선택하고 제약조건에 따라 반복적으로 전파함으로써 해결책을 찾을 수 있다.이 알고리즘은 이미 할당된 변수에 값을 할당하려고 하지 않는다. 그것은 제약 네트워크의 사이클의 존재를 암시하기 때문이다.
유사한 조건이 경로 일관성을 유지한다.호 일관성과 경로 일관성을 강화하여 만족도를 확립할 수 있는 특례는 다음과 같다.
- 호 일관성을 적용하면 주기가 없는 이항 구속조건(이항 구속조건의 트리)으로 만들어진 문제의 만족도가 설정된다.
- 경로 일관성을 적용하면 이진 도메인의 이진 제약 조건(주기에 따라 다름)에 대한 만족도가 설정된다.
- 강력한 일관성을 적용하면 변수를 포함하는 문제의 만족도가 설정된다.
특례
상대적 일관성에 대한 일부 정의나 결과는 특별한 경우에만 적용된다.
도메인이 정수로 구성되면 바인딩된 일관성을 정의할 수 있다.이러한 형태의 일관성은 도메인의 극단값, 즉 변수가 취할 수 있는 최소값과 최대값의 일관성에 기초한다.
제약조건이 대수학이나 부울인 경우, 호 일관성은 새로운 제약조건을 추가하거나 구 제약조건을 구문적으로 수정하는 것과 동등하며, 이는 적절하게 제약조건을 구성함으로써 이루어질 수 있다.
특화된 제약조건
어떤 종류의 제약이 일반적으로 사용된다.예를 들어 일부 변수가 모두 다르다는 제약조건이 자주 사용된다.그러한 제약조건에 대한 아크 일관성을 강화하기 위한 효율적인 전문 알고리즘이 존재한다.
여러 변수를 다르게 적용하기 위한 은 d f e ( 1,… , ) {\}) 또는 {n 또는alldifferent([X1,...,Xn]). 이 제약조건은 모든 j {\=에 대해 변수의 모든 쌍의 비균등성과 동등하다 변수의 도메인이 단일 으로 축소되었을 때, enf가 제약조건 전파에 의해 다른 모든 도메인에서 이 값을 제거할 수 있다.오싱 호 일관성.특화된 제약조건의 사용은 개별적인 이항적합성 질환을 보유하지 않는 특성을 이용할 수 있게 한다.
첫 번째 속성은 모든 변수의 도메인에 있는 요소의 총 개수가 최소한 변수의 개수가 되어야 한다는 것이다.더 정확히 말하면, 호 일관성을 시행한 후, 할당되지 않은 변수의 수는 해당 도메인의 결합에 있는 값의 수를 초과해서는 안 된다.그렇지 않으면 제약조건을 충족시킬 수 없다.이 조건은 의 제약조건에서 쉽게 확인할 수 있다.alldifferent형태, 그러나 질병 네트워크의 호 일관성에는 부합하지 않는다.싱글의 두 번째 재산alldifferent제약조건은 초당적 매칭 알고리즘을 사용하여 하이퍼 통합 일관성을 효율적으로 확인할 수 있다는 것이다.특히 두 노드 세트로 변수와 값을 가진 그래프가 구축돼 있고, 여기에 전문화된 초당적 그래프 매칭 알고리즘을 가동해 이러한 매칭의 존재 여부를 확인한다.
일반적으로 사용되는 다른 종류의 제약조건은cumulative1. 일정 수립과 배치의 문제를 위해 도입되었다.예를 들면,cumulative([S1,...,Sm], [D1,...,Dm], [R1,...,Rm], L)있는 조건을 공식화하는 데 사용할 수 있다.m각각 시작 시간이 있는 활동si, 지속시간di그리고 금액 사용ri자원의제약조건에 따르면 가용한 자원의 총량은L. 누적 제약조건에 대한 전문 제약조건 전파기술이 존재하며, 어떤 가변영역이 이미 단일값으로 축소되었는가에 따라 다른 기법이 사용된다.
제약조건 로직 프로그래밍에 사용되는 세 번째 전문 제약조건은element1. 제약조건 로직 프로그래밍에서 리스트는 변수의 값으로 허용된다.A 제약element(I, L, X)하면 만족하다L목록이고X이다I-이 목록의 -번째 요소.이러한 제약조건에 대한 전문 제약조건 전파 규칙이 존재한다.예를 들면,L그리고I단일 값 도메인으로 축소됨, 즉X판별할 수 있다보다 일반적으로, 불가능한 값들X 의 도메인에서 유추할 수 있으며, 그 반대의 경우도 가능하다.
방향 일관성
방향 일관성은 주어진 변수 순서에 따라 값을 변수에 할당하는 알고리즘에 의해 사용되도록 조정된 호, 경로 및 i의 일관성 변형이다.이들은 비방향 변수와 유사하지만 일부 변수에 대한 일관된 할당을 순서에 따라 자신보다 큰 다른 변수에 일관되게 확장시킬 수 있어야만 한다.
방향 호 및 경로 일관성
알고리즘이 x ,…, 순서로 변수를 평가하는 경우 일관성(consistency)은 낮은 색인 변수의 값이 모두 높은 색인 변수의 값과 일치함을 보장할 때만 유용하다.
변수에 대한 값을 선택할 때 지정되지 않은 변수의 모든 값과 일치하지 않는 값은 무시될 수 있다.실제로 이러한 값이 모두 현재의 부분평가와 일치하더라도 알고리즘은 나중에 할당되지 않은 변수에 대한 일관된 값을 찾지 못할 것이다.한편, 이미 평가된 변수와의 일관성을 강제할 필요는 없다: 알고리즘이 현재의 부분 평가와 일치하지 않는 값을 선택하면, 어쨌든 불일치가 감지된다.
는 변수의 평가의 질서는 x1이라고 가정한다면…,)n{\displaystyle x_{1},\ldots ,x_{n}}, 모든 변수)나는}{\displaystyle x_{나는}아크 다른 변수와 같이 j{\displaystyle x_{j}} 같은 전 < 일관된 제약 조건 충족 문제 방향 arc 일치한다;j. {\displaystyle i<. j}. 지향성 경로 일관성만 한다면, 나는, j<>z{\displaystyle i,j<, z}두개의 변수 i)j{\displaystyle x_{나는},x_{j}}가 되기 경로 xz{\displaystyle x_{z}과 일관된}일 경우 가지고 있다. 강한 방향 경로 일관성 둘 다 방향 경로의 일관성과 directi을 의미하 x 비슷하다.onal 아크일관성다른 형태의 일관성에 대해서도 유사한 정의를 내릴 수 있다.
호 및 경로 일관성을 위한 제약 조건 전파
방향 호 일관성을 시행하는 제약 조건 전파는 마지막 단계부터 첫 단계까지의 변수에 대해 반복하며, 각 단계에서 낮은 지수의 모든 변수의 호 일관성을 시행한다.변수의 순서가 ,… , n 인 경우, 이 은 n{\에서 1}까지 변수에 대해 한다 가 있는
 | 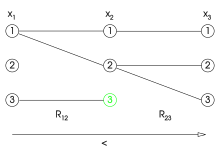 |  |
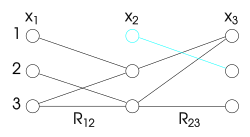
| 방향 호 일관성이 없는 인스턴스: = }이가) 2{\}=의 값과 일치하지 않는 경우 = 에 제약 조건이 없음및 3 가장자리가 생략됨). | 방향 호 일관성 적용은 로 시작하여 }= 값을 제거하여 3과(와) 일치하도록 한다 | 호 일관성 시행은 x = 3 이(가) 이미 제거되었기 때문에 x = 2 및 1= 이 모두 제거된다. |
방향 경로 일관성 및 강한 방향 경로 일관성은 호 일관성을 위한 알고리즘과 유사한 알고리즘에 의해 시행될 수 있다.로 나는, j<>z{\displaystyle i,j<, z}, 그리고 그들의 xz와 경로 일관성으로 간주된다{\와 같이 그들은 모든 변수가)z{\displaystyle x_{z}}는 두개의 변수,)j{\displaystyle x_{나는},x_{j}나는 x})n{\displaystyle x_{n}}x1{\displaystyle x_{1}}까지 변수들을 처리합니다.displ를 시행한다.문제가 와 사이에 아무런 제약조건이 xj {\j}와 xj {\ 사이에 제약조건이 없는 경우에는 조작할 필요가 없다 그러나 x 와 x_} 사이에 제약조건이 없다. 사소한 것으로 가정한다.제약 조건 전파가 만족스러운 할당 세트를 줄이면 효과적으로 새로운 비경쟁적 제약 조건을 생성한다.강한 방향 경로 일관성을 강제하는 제약 조건 전파도 유사하지만 호 일관성도 강제한다.
방향 일관성 및 만족도
방향 일관성은 제약조건을 만족하는 부분적인 해결책이 높은 지수의 또 다른 변수로 일관되게 확장될 수 있음을 보장한다.그러나 서로 다른 변수에 대한 확장이 서로 일치한다고 보장하지는 않는다.예를 들어, 부분 솔루션은 변수 x 또는 변수 까지 일관되게 확장될 수 있지만, 이 두 확장자는 서로 일관성이 없다
이런 일이 일어나지 않는 경우는 두 가지인데, 지향적인 일관성은 도메인이 비어 있지 않고 제약이 만족스럽지 않으면 만족을 보장한다.
첫 번째 경우는 제약조건의 순서가 지정된 그래프를 폭 1로 만드는 변수의 순서에 따른 이항 제약조건 문제의 경우다.그러한 순서는 제약조건의 그래프가 나무인 경우에만 존재한다.이 경우, 그래프의 너비는 노드가 결합되는 최대 하위 노드 수(순서에 따라)를 제한한다.방향 호 일관성은 변수에 대한 모든 일관된 할당이 더 높은 노드로 확장될 수 있음을 보장하며, 너비 1은 한 노드가 둘 이상의 하위 노드에 결합되지 않음을 보장한다.결과적으로, 일단 하위 변수가 할당되면, 그 값은 결합되는 모든 상위 변수까지 일관되게 확장될 수 있다.이 연장은 나중에 불일치로 이어질 수 없다.실제로 그래프에 너비 1이 있으므로 다른 하위 변수는 더 높은 변수에 결합되지 않는다.
결과적으로 제약조건 문제가 변수의 순서(해당 그래프가 트리임을 의미함)와 관련하여 폭 1을 가지고 있고, 동일한 순서에 대해 방향적으로 호를 일관되게 하는 문제가 있다면, 순서(있는 경우)에 따라 변수를 반복적으로 할당함으로써 해결책(있는 경우)을 찾을 수 있다.
도메인이 비어 있지 않고 제약조건이 만족스럽지 않을 경우 방향 일관성이 만족을 보장하는 두 번째 경우는 강한 방향 경로 일관성을 사용하여 그래프에서 폭 2를 유도한 이항 구속조건 문제의 경우다.실제로 이러한 형태의 일관성은 변수나 변수 쌍에 대한 모든 할당을 더 높은 변수로 확장할 수 있음을 보장하며, 너비 2는 이 변수가 다른 한 쌍의 더 낮은 변수에 결합되지 않음을 보장한다.
폭 대신 유도 폭을 고려하는 이유는 방향 경로 일관성을 강화하면 제약을 추가할 수 있기 때문이다.실제로 두 변수가 동일한 제약조건에 있지 않지만 더 높은 변수와 함께 제약조건에 있는 경우, 해당 값의 일부 쌍은 경로 일관성을 위반할 수 있다.그러한 쌍을 제거하면 새로운 제약조건이 생긴다.결과적으로 제약 조건 전파는 그래프가 원래 그래프보다 더 많은 에지를 갖는 문제를 야기할 수 있다.그러나 이 모든 가장자리는 모두 동일한 노드의 두 부모 사이에 있으므로 유도 그래프에 반드시 표시된다.폭 2는 모든 일관성 있는 부분 평가를 솔루션으로 확장할 수 있음을 보장하지만, 이 폭은 생성된 그래프에 상대적이다.그 결과, 해결책의 존재를 보장하기 위한 강력한 방향 경로 일관성을 위해 유도 폭 2가 필요하다.
방향 I-일관성
방향 - 일관성은 - 1 변수에 대한 모든 일관성 있는 할당이 순서에서 더 높은 다른 변수에 일관되게 확장될 수 있다는 보장이다. 방향 -일관성은 유사한 방식으로 정의되지만 최대 i - 변수의 모든 그룹이 고려된다.문제가 강력한 i - 일관성이 있고 이 i 보다 작고 빈 도메인이나 불만족스러운 제약 조건이 없는 경우 해결책이 있다.
모든 문제는 방향 - 일관성이 강한 방향으로 만들어질 수 있지만, 이 작업을 수행하면 해당 그래프의 폭이 커질 수 있다.방향 정합성을 강제하는 제약 조건 전파 절차는 방향 호 일관성 및 경로 정합성에 사용되는 절차와 유사하다.순서에 따라 마지막에서 첫 번째에 이르기까지 변수를 차례대로 고려한다.변수 의 경우 알고리즘은 보다 낮은 인덱스를 가지고 있고 k 제약조건에 있는 - 1 변수의 모든 그룹을 고려한다 {\}과 이러한 변수의 일관성을 확인하고 po.이러한 모든 변수 사이의 제약조건에서 만족스러운 할당을 제거하여 ssily 시행(있는 경우 또는 그렇지 않은 경우 새 할당을 생성).
이 절차는 강력한 방향 일관성 있는 인스턴스를 생성한다.그러나 이 경우 새로운 제약조건이 추가될 수도 있다.따라서 원래 문제의 가 i{\인 경우에도 결과 인스턴스의 너비가 더 클 수 있다만약 그렇다면, 지향성 강한 일관성은 도메인이 비어 있지 않고 제약조건이 만족스럽지 않더라도 만족감을 의미하지 않는다.
그러나 제약조건 전파는 현재 고려 중인 변수보다 낮은 변수에만 제약조건을 추가한다.결과적으로 알고리즘이 이 변수를 처리한 후에는 변수에 대한 제약조건이 수정되거나 추가되지 않는다.고정 을를) 고려하는 대신 고려된 각 변수의 부모 수로 수정할 수 있다(변수의 부모는 변수보다 낮고 변수와 제약에 있는 지수의 변수임).이는 각 단계에서 주어진 변수의 모든 부모를 고려하는 것과 일치한다.즉, 마지막부터 까지의각 x i {\displaystyle 에 대해 모든 부모들이 x 와 일치하는 값으로 자신의 값을 제한하는 새로운 제약조건에 포함된다 이 알고리즘은 변수i {\}을(를) 가진 수정으로 볼 수 있기 때문이다.각 노드의 부모 수로 변경되는 을(를) 적응 일관성이라고 한다.
이 알고리즘은 문제의 유도 폭과 동일한 과(와) 강력한 방향 displaystyle i을(를) 적용한다.도메인이나 제약 조건이 비어 있지 않은 경우에만 결과 인스턴스를 만족시킬 수 있다.이 경우 할당되지 않은 변수를 임의의 값으로 반복적으로 설정하고, 이 부분 평가를 다른 변수에 전파함으로써 해결 방법을 쉽게 찾을 수 있다.강한 방향 일관성을 시행하여 도입된 제약조건의 수가 기하급수적으로 크기를 증가시킬 수 있기 때문에 이 알고리즘이 항상 다항식 시간인 것은 아니다.그러나 강력한 방향 일관성을 시행하는 것이 인스턴스를 엄청나게 확대시키지 않는 다항 시간에는 문제가 해결될 수 있다.그 결과, 한 인스턴스가 상수에 의해 경계된 폭을 유도했다면 다항 시간 내에 해결할 수 있다.
버킷 제거
버킷 제거는 만족도 알고리즘이다.적응형 일관성의 개편으로 정의할 수 있다.그것의 정의는 각각의 변수가 연관된 버킷을 가지고 있는 제약조건용 컨테이너인 버킷을 사용한다.제약조건은 항상 가장 높은 변수의 버킷에 속한다.
버킷 제거 알고리즘은 가장 높은 변수에서 가장 낮은 변수로 차례로 진행된다.각 단계에서 이 변수 의 버킷의 제약조건이 고려된다.정의상 이러한 제약조건은 x 보다 낮은 변수만 포함한다알고리즘은 이러한 하한 변수들 사이의 제약조건을 수정한다(있는 경우, 그렇지 않은 경우 새로운 변수를 만든다).특히 x 의 버킷의 제약조건과 일관되게 displaystyle }까지 값을 확장하도록 강제한다이 새로운 제약조건이 있다면 적절한 버킷에 넣는다.이 제약조건은 보다 낮은 변수만을 포함하므로 x 보다 낮은 변수의 버킷에 추가된다
이 알고리즘은 적응형 일관성을 강화하는 것과 같다.둘 다 변수의 일관성을 모든 부모에게 강요하고, 변수를 고려한 후에 새로운 제약조건이 추가되지 않기 때문에 어떤 결과는 역추적 없이 해결될 수 있는 인스턴스다.
그들이 생성하는 인스턴스의 그래프는 유도 그래프의 하위 그래프이기 때문에, 유도 폭에 상수가 경계를 이루면 생성된 인스턴스는 원래 인스턴스의 크기에서 다항식의 크기가 된다.결과적으로, 인스턴스의 유도 폭에 상수가 경계를 이루면, 그것을 푸는 것은 두 알고리즘에 의해 다항 시간 내에 이루어질 수 있다.
관계 일관성
일관성에 대한 이전의 정의는 모두 임무의 일관성에 관한 것이지만, 관계적 일관성은 주어진 제약조건이나 제약조건들의 집합의 만족만을 포함한다.더 정확히 말하면, 관계적 일관성은 모든 일관적인 부분 배분이 주어진 제약조건이나 제약조건 집합이 충족되는 방식으로 확장될 수 있다는 것을 의미한다.으로 X 에 대한 모든 일관성 있는 할당이 C 에 될 수 있는 변수 X {\ 에 대한 제약 C 에 대한 제약 조건 C 과 관계형 호가 일치한다.만족하다"일반" 일관성과 관계형 호 일관성 사이의 차이는 후자는 주어진 제약조건을 만족시키기 위해 확장된 할당만 요구하는 반면, 전자는 모든 관련 제약조건을 만족시키기 위해 이를 요구한다.
이 정의는 둘 이상의 제약조건과 둘 이상의 변수로 확장될 수 있다.특히 관계 경로 일관성은 관계형 호-일관성과 유사하지만, 하나의 제약조건 대신 두 가지 제약조건이 사용된다.두 제약조건은 변수와의 관계 경로로서, 모든 변수들에 대한 일관된 할당과 고려된 변수들이 두 제약조건이 충족되는 방식으로 확장될 수 있다.
세 가지 이상의 제약조건에 대해 m - 일관성이 정의된다.관계형 - 일관성에는 일련의 제약 조건과 이러한 모든 제약 조건의 범위에 있는 변수가 포함된다.특히 이러한 제약조건은 해당 범위에 있는 다른 모든 변수에 대한 모든 일관성 있는 할당이 이러한 제약조건이 충족되는 방식으로 변수에 확장될 수 있는 경우 변수와 하는관계형 m {\ m}이다.문제는 모든 제약 조건이 모든 범위에 모든변수와 하는 관계형 m {\displaystyle 인 경우 m 관계형 일관성이다.한 m 일관성은 위와 같이 정의된다 k {\displaystyle 의 속성으로서 모든 < .
관계 일관성은 또한 한 변수 대신 더 많은 변수에 대해 정의될 수 있다. 중 의 하위 집합에 대한 모든 일관성 있는 할당이 모든 제약 조건을 충족하는 모든 변수에 대한 평가로 확장될 수 있는 경우 m m} 제약 조건 집합은 관계형, ) 일관성이 있다.평가가 확장 가능해야 하는 변수가 관련 제약조건의 모든 범위에 반드시 포함되는 것은 아니기 때문에 이 정의가 위의 정의를 정확하게 확장하는 것은 아니다.
변수의 순서가 주어진 경우, 관계 일관성은 변수의 순서에 따라 다른 변수의 평가를 확장 가능해야 하는 경우로 제한될 수 있다.이 수정된 조건을 방향 관계 일관성이라고 한다.
관계적 일관성 및 만족도
제약조건 만족도 문제는 관계적으로 일관성이 있을 수 있고, 빈 영역이나 불만족스러운 제약이 없을 수 있지만, 여전히 불만족스러울 수 있다.그러나 이것이 가능하지 않은 경우도 있다.
첫 번째 경우는 도메인이 최대 요소를 포함할 때 강력한 관계형 일관성 있는 문제의 경우다.이 경우 변수에 대한 일관된 평가는 항상 다른 단일 변수로 확장될 수 있다. = ,… , k= k}=a_{이(가) 그러한 평가이고 x + }이(가) 변수가 될 경우 가능한 만 이러한 모든 값이 평가와 일치하지 않는 경우, 평가에 의해 위반되는 비필요적으로 고유한) 제약조건과 가능한 값 중 하나가 있다.따라서 강력한 -또는 그 이하의 제약조건을 충족하도록 평가를 확장할 수 없으며, 이는 강력한 관계형 m - 일관성 조건을 위반하는 것이다.
두 번째 경우는 도메인이 아닌 제약조건의 측정에 관련된다.제약조건은 다른 변수의 가능한 모든 값 또는 최대 의 m 에 의해 제약조건을 충족하도록 한 한 변수(하나의 변수)에 대한 모든 평가를 확장할 수 있는 경우 m이(가) 조인다. -긴축 제약 조건이 강하게 관계적으로 + - 일관성이 있는 경우에만 문제가 충족된다.
세 번째 경우는 행-콘벡스 행렬로 나타낼 수 있는 이항 구속조건이다.이진 제약조건은 투차원 매트릭스 으로 나타낼 수 있으며 여기서 displaystyle 값 x i 및 값에 따라 dissty}이 0 또는 1이 된다.x_{는 제약 조건을 만족시킨다.이 행렬의 행은 1이 포함된 연속형일 때 볼록하다(공식적으로 두 원소가 1이면 그 사이의 모든 원소도 1이다).행렬은 모든 행이 볼록한 경우 볼록한 행이다.
만족도와 동등한 강한 관계 경로 일관성을 만드는 조건은 모든 제약을 행 볼록 행렬로 나타내도록 만드는 변수의 순서가 존재하는 제약조건 만족도 문제의 조건이다.이 결과는 공통 요소를 쌍으로 갖는 볼록한 행 집합도 글로벌 공통 요소를 가지고 있다는 사실에 기초한다. 변수에 대한 평가를 고려할 때 일부 제약조건에서 일부 행을 선택하여 + -th번째 변수에 대해 허용되는 값을 제공한다.특히 변수 중 모든 변수에 k + 과 관련된 제약 조건을 나타내는 행렬의 값에 상대적인 행은 후자의 허용 값을 나타낸다.이러한 행은 볼록하고 경로 일관성 때문에 쌍방향으로 공통 요소를 가지므로 공유된 공통 요소를 가지기도 하는데, 이는 다른 행과 일치하는 마지막 변수의 값을 나타낸다.
로컬 일관성 사용
모든 형태의 국소 일관성은 제약 조건 전파에 의해 집행될 수 있으며, 제약 조건을 만족시키는 변수 및 할당 세트의 영역을 축소할 수 있고 새로운 제약 조건을 도입할 수 있다.제약 조건 전파가 빈 영역이나 불만족스러운 제약 조건을 만들 때마다 원래의 문제는 불만족스럽다.따라서, 모든 형태의 지역 일관성은 만족도의 근사치로 사용될 수 있다.더 정확히 말하면, 그것들은 불완전한 불만족 알고리즘으로 사용될 수 있는데, 그들은 어떤 문제가 불만족스럽다는 것을 증명할 수 있지만, 일반적으로 어떤 문제가 만족스럽다는 것을 증명할 수 없기 때문이다.이러한 근사 알고리즘은 검색 알고리즘(백트랙팅, 백점핑, 로컬 검색 등)에 의해 더 이상 분석하지 않고도 부분 솔루션을 모든 제약조건을 충족하도록 확장할 수 있는지 여부를 알려주는 경험적 접근법으로 사용될 수 있다.
제약조건 전파가 빈 도메인이나 불만족스러운 제약조건을 생성하지 않더라도, 그럼에도 불구하고 도메인을 감소시키거나 제약조건을 강화시킬 수 있다.이럴 경우 문제의 검색공간이 줄어들어 문제 해결에 필요한 검색량이 줄어든다.
국소 일관성은 제한된 일부 사례에서 만족도를 입증한다(제약 만족도의 복잡성#제한 참조).이것은 어떤 특별한 종류의 문제나 지역적 일관성의 경우에 해당된다.예를 들어, 이항 반복 문제에 호 일관성을 적용하면 문제가 만족스러운지 여부를 알 수 있다.강력한 방향 - 일관성을 적용하면 동일한 순서에 따라 i- 을(를) 유발한 문제의 만족도를 알 수 있다.적응형 방향 일관성은 임의의 문제의 만족도를 말해준다.
참고 항목
외부 링크
참조
- Lecoutre, Christophe (2009). Constraint Networks: Techniques and Algorithms. ISTE/Wiley. ISBN 978-1-84821-106-3
- Dechter, Rina (2003). Constraint processing. Morgan Kaufmann. ISBN 1-55860-890-7
- Apt, Krzysztof (2003). Principles of constraint programming. Cambridge University Press. ISBN 0-521-82583-0
- Marriott, Kim; Peter J. Stuckey (1998). Programming with constraints: An introduction. MIT Press. ISBN 0-262-13341-5














 도메인에 값
도메인에 값






 (는) x
(는) x





 도메인에서 유추할 수 있으며, 그 반대의 경우도 가능하다.
도메인에서 유추할 수 있으며, 그 반대의 경우도 가능하다. 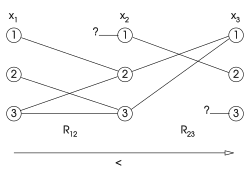











 대한 제약 조건 C
대한 제약 조건 C