선인장 그래프
Cactus graph그래프 이론에서 선인장(선인장 나무라고도 함)은 어떤 두 개의 단순한 사이클이라도 최대 하나의 꼭지점을 공통적으로 갖는 연결된 그래프다.동등하게, 모든 가장자리가 최대 하나의 단순한 사이클에 속하는 연결된 그래프 또는 (비경쟁 선인장의 경우) 모든 블럭(컷-버텍스 없는 최대 서브그래프)이 에지 또는 사이클인 그래프다.
특성.
선인장은 외행성 그래프다.모든 가성비는 선인장이다.비경쟁 그래프는 모든 블럭이 단순한 주기 또는 단일 가장자리인 경우에만 선인장이다.
각 성분이 선인장인 그래프 계열은 그래프 사소한 작업에 따라 아래로 닫힌다.이 그래프 계열은 하나의 금지된 단조로 특징지어질 수 있는데, 전체 그래프 K에서4 가장자리를 제거하여 형성된 네 개의 버텍스 다이아몬드 그래프로 구성된다.[1]
삼각선인장
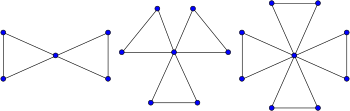
삼각형 선인장은 선인장 그래프의 특별한 유형으로 각 주기의 길이는 3이고 각 가장자리는 주기에 속한다.예를 들어, 우정의 그래프, 즉 삼각형의 집합으로 이루어진 그래프는 삼각형 선인장이다.선인장 그래프가 되는 것뿐만 아니라 삼각형 선인장 역시 블록 그래프와 국소 선형 그래프다.
삼각형 선인장은 일치하는 선인장이 제거되더라도 계속 연결되는 특성을 가지고 있다. 주어진 정점 수만큼 선인장은 이 특성에서 가능한 가장자리가 가장 적다.정점 수가 홀수인 모든 트리는 삼각형 선인장에 가장자리를 추가하여 증축할 수 있으며, 매칭 제거 후에도 연결된 상태로 남아 있는 특성으로 최소 증축이 가능하다.[2]
어떤 그래프에서든 가장 큰 삼각형 선인장은 다항식 시간에 모항 패리티 문제에 대한 알고리즘을 사용하여 찾을 수 있다.삼각형 선인장 그래프는 평면 그래프이기 때문에 가장 큰 삼각형 선인장은 평면화의 중요한 하위 문제인 가장 큰 평면 하위 그래프에 근사치로 사용할 수 있다.근사 알고리즘으로서, 이 방법은 최대 평면형 서브그래프 문제로 가장 잘 알려진 근사비 4/9를 가진다.[3]
가장 큰 삼각형 선인장을 찾는 알고리즘은 이 가장 큰 선인장의 삼각형 수를 특징짓는 로바스와 플럼머의 정리와 관련이 있다.[4]Lovasz와 Flummer는 그래프의 모든 삼각형이 정점 파티션의 단일 클래스에 정점 두 개 또는 에지 파티션의 단일 클래스에 모두 세 개의 에지를 갖는 속성을 가진 주어진 그래프의 정점과 가장자리 쌍을 부분 집합으로 고려한다. 그들은 이 속성을 유효한 파티션 쌍이라고 부른다.Then the number of triangles in the largest triangular cactus equals the maximum, over pairs of valid partitions and , of
- = - 1) 2+ n- ,
여기서 은(는) 주어진 그래프의 정점 수이고 i 은(는) 클래스E i {\ E_에 의해 충족되는 정점 클래스의 수입니다
최근 빡빡한 극치 행 그 어떤 비행기 그래프 G{G\displaystyle}, 항상 선인장 부분 그래프 C⊆ G{C\subseteq G\displaystyle}G{G\displaystyle}의 삼각형 얼굴을 최소한 1/6{1/6이기\displaystyle}분수가 있다. 이한 직접적인 항문이 존재하는 것으로 나타났다 proven[5]다.ysi위의 최소-최대 공식을 사용하지 않고 최대 평면 서브그래프 문제에 대한 4/9 근사 알고리즘의 s.
로자의 추측
삼각형 선인장과 관련된 중요한 추측은 모든 삼각형 선인장이 우아하거나 거의 우아하다고 말하는 알렉산더 로자의 이름을 딴 로자의 추측이다.[6]더 정확하게
t t 0, 1모드 4블록의 삼각형 선인장은 모두 우아하고 t t 2, 3모드 4블록의 선인장은 거의 우아하다.
알고리즘 및 응용 프로그램
일반 그래프의 경우 NP-hard인 설비 위치 문제와 선인장의 경우 다항 시간 내에 일부 그래프 문제를 해결할 수 있다.[7][8]
선인장은 외부 평면 그래프의 특별한 경우이기 때문에, 선인장은 다항 시간 내에 그래프 상의 여러 조합 최적화 문제를 해결할 수 있다.[9]
선인장은 유용한 특성을 가진 전기 회로를 나타낸다.선인장의 초기 적용은 op-amps의 표현과 관련이 있었다.[10][11][12]
선인장은 또한 다른 게놈들 간의 관계나 게놈의 일부 사이의 관계를 나타내는 방법으로 비교 게놈학에도 최근 이용되고 있다.[13]
선인장이 연결되어 있고, 각각의 꼭지점이 최대 두 블록에 속한다면, 그것은 크리스마스 선인장이라고 불린다.모든 polyhedral 그래프, Moitra은 모든 polyhedral 그래프는 유클리드의 비행기, 좌표의 탐욕스러운 포워딩 메시지 betw 추적하다 vertices에 대한 과제를 계기로 욕심 많은던 1가지 이슈 때문이었습니닸다(2010년)모든 vertices의 레이턴 및다 증거에 필수적인 역할을 하고 있는 사실을 포함하는 가재발 선인장 부분 그래프고 있다.een꼭지점 [14]쌍
위상 그래프 이론에서 세포 임베딩이 모두 평면인 그래프는 정확히 선인장 그래프의 하위 계열이며, 각 정점이 최대 한 사이클에 속하는 추가 속성이 있다.이 그래프에는 다이아몬드 그래프와 5Verex 우정 그래프라는 두 개의 금지된 미성년자가 있다.[15]
역사
선인장은 처음에 후시미 나무라는 이름으로 연구되었는데, 프랭크 하라리와 조지 유진 울렌벡이 이 그래프들에 대한 이전 연구들을 기리기 위해 선인장 나무들에 의해 수여되었다.[16][17]같은 하라리-Uhlenbeck paper는 모든 주기가 삼각형인 이 유형의 그래프에 "cactus"라는 이름을 붙이지만, 이제는 모든 길이의 사이클을 허용하는 것이 표준이다.
한편, 후시미 트리라는 이름은 일반적으로 모든 블록이 완전한 그래프인 그래프를 가리키게 되었다(동일하게, 다른 그래프에 있는 블록의 교차 그래프).이러한 용법은 후시미의 작업과 거의 관련이 없으며, 현재 이 가족에게는 더욱 적절한 용어 블록 그래프가 사용되고 있다. 그러나, 이러한 모호성 때문에 이 문구는 선인장 그래프를 언급하는 데 덜 자주 쓰이게 되었다.[18]
참조
- ^ El-Mallah, Ehab; Colbourn, Charles J. (1988), "The complexity of some edge deletion problems", IEEE Transactions on Circuits and Systems, 35 (3): 354–362, doi:10.1109/31.1748
- ^ Farley, Arthur M.; Proskurowski, Andrzej (1982), "Networks immune to isolated line failures", Networks, 12 (4): 393–403, doi:10.1002/net.3230120404, MR 0686540
- ^ Călinescu, Gruia; Fernandes, Cristina G; Finkler, Ulrich; Karloff, Howard (2002), "A Better Approximation Algorithm for Finding Planar Subgraphs", Journal of Algorithms, 2, 27 (2): 269–302, CiteSeerX 10.1.1.47.4731, doi:10.1006/jagm.1997.0920, S2CID 8329680
- ^ Lovász, L.; Plummer, M.D. (2009), Matching Theory, AMS Chelsea Publishing Series, ISBN 9780821847596
- ^ Chalermsook, Parinya; Schmid, Andreas; Uniyal, Sumedha (2019), "A Tight Extremal Bound on the Lovasz Cactus Number in Planar Graphs", CoRR, abs/1804.03485, arXiv:1804.03485, doi:10.4230/LIPIcs.STACS.2019.19, S2CID 4751972
- ^ Rosa, A. (1988), "Cyclic Steiner Triple Systems and Labelings of Triangular Cacti", Scientia, 1: 87–95.
- ^ Ben-Moshe, Boaz; Bhattacharya, Binay; Shi, Qiaosheng (2005), "Efficient algorithms for the weighted 2-center problem in a cactus graph", Algorithms and Computation, 16th Int. Symp., ISAAC 2005, Lecture Notes in Computer Science, vol. 3827, Springer-Verlag, pp. 693–703, doi:10.1007/11602613_70, ISBN 978-3-540-30935-2
- ^ Zmazek, Blaz; Zerovnik, Janez (2005), "Estimating the traffic on weighted cactus networks in linear time", Ninth International Conference on Information Visualisation (IV'05), pp. 536–541, doi:10.1109/IV.2005.48, ISBN 978-0-7695-2397-2, S2CID 15963409
- ^ Korneyenko, N. M. (1994), "Combinatorial algorithms on a class of graphs", Discrete Applied Mathematics, 54 (2–3): 215–217, doi:10.1016/0166-218X(94)90022-1. BSSR 과학 아카데미의 통지에서 번역됨, 세르. 물리-수학. Sci, (1984) No. 3, 페이지 109-111 (러시아어)
- ^ Nishi, Tetsuo; Chua, Leon O. (1986), "Topological proof of the Nielsen-Willson theorem", IEEE Transactions on Circuits and Systems, 33 (4): 398–405, doi:10.1109/TCS.1986.1085935
- ^ Nishi, Tetsuo; Chua, Leon O. (1986), "Uniqueness of solution for nonlinear resistive circuits containing CCCS's or VCVS's whose controlling coefficients are finite", IEEE Transactions on Circuits and Systems, 33 (4): 381–397, doi:10.1109/TCS.1986.1085934
- ^ Nishi, Tetsuo (1991), "On the number of solutions of a class of nonlinear resistive circuit", Proceedings of the IEEE International Symposium on Circuits and Systems, Singapore, pp. 766–769
- ^ Paten, Benedict; Diekhans, Mark; Earl, Dent; St. John, John; Ma, Jian; Suh, Bernard; Haussler, David (2010), "Cactus Graphs for Genome Comparisons", Research in Computational Molecular Biology, Lecture Notes in Computer Science, vol. 6044, pp. 410–425, doi:10.1007/978-3-642-12683-3_27, ISBN 978-3-642-12682-6
- ^ Leighton, Tom; Moitra, Ankur (2010), "Some Results on Greedy Embeddings in Metric Spaces" (PDF), Discrete & Computational Geometry, 44 (3): 686–705, doi:10.1007/s00454-009-9227-6, S2CID 11186402.
- ^ Nordhaus, E. A.; Ringeisen, R. D.; Stewart, B. M.; White, A. T. (1972), "A Kuratowski-type theorem for the maximum genus of a graph", Journal of Combinatorial Theory, Series B, 12 (3): 260–267, doi:10.1016/0095-8956(72)90040-8, MR 0299523
- ^ Harary, Frank; Uhlenbeck, George E. (1953), "On the number of Husimi trees, I", Proceedings of the National Academy of Sciences, 39 (4): 315–322, Bibcode:1953PNAS...39..315H, doi:10.1073/pnas.39.4.315, MR 0053893, PMC 1063779, PMID 16589268
- ^ Husimi, Kodi (1950), "Note on Mayers' theory of cluster integrals", Journal of Chemical Physics, 18 (5): 682–684, Bibcode:1950JChPh..18..682H, doi:10.1063/1.1747725, MR 0038903
- ^ 예를 들어, MR0659742는 다른 정의를 사용한 논문의 1983년 로버트 E. 제이미슨이 쓴 리뷰로, 모호성을 메흐디 베자드와 게리 차르트랑의 책에 있는 오류로 귀속시킨다.




 (는) 주어진 그래프의 정점 수이고
(는) 주어진 그래프의 정점 수이고  (는)
(는)