결점 유형에는 결정 불연속성을 야기하는 유한한 재료 크기 때문에 표면에서 가장 빈번하게 발생하는 원자 공실, 아다텀, 스텝, 꼬임 등이 포함된다. 표면 결함이든 대량 결함이든 모든 유형의 결함에 공통점이 있는 것은 대량과는 다른 특정 전자 에너지 수준을 가진 매달린 결합을 생산한다는 점이다. 이러한 차이는 표면 바로 바깥의 이온 코어가 없어져 발생하는 전자 전위 에너지의 변화로 인해 주기적인 Bloch 파동으로 이러한 상태를 설명할 수 없기 때문에 발생한다. 따라서 이것들은 전자 에너지가 적절하게 설명될 수 있도록 슈뢰딩거 방정식에 대한 별도의 해법이 필요한 국부적 상태들이다. 주기가 깨지면 불량 산란으로 전도도가 감소한다.
반도체 매달림 본드의 전자 에너지 수준

그림 1: Si crystal을 형성하는 다양한 단계에서 전자 에너지의 해리슨 에너지 다이어그램. 수직축은 에너지다. 3초와 3p 궤도는 하나의 Si 원자에서 혼합되는데, 2 3초 전자가 2 3p 전자가 잃는 것보다 더 많은 에너지를 얻기 때문에 에너지적으로 불리하다. 유리한 조광기 형성은 본딩 (b)과 안티 본딩 (b*) 상태를 형성하여 마침내 순 에너지 손실을 초래하고 후속 원자 첨가는 결정 형성 전도(CB)와 발랑스 밴드(VB)를 형성한다. 매달린 본드 상태(db)는 누락된 sp3 본드에 해당한다. 매달려 있는 결합 에너지 수준을 결정하는 더 간단하고 질적인 방법은 해리슨 도표를 사용하는 것이다.[1][2] 금속은 비방향 결합과 작은 데비 길이 때문에 그것들이 존재한다고 간주될 수 있다면 매달려 있는 결합을 하찮게 만든다. 반도체는 전자가 느끼고 결함 에너지 상태에 갇힐 수 있는 유전체다. 이들 상태의 에너지 수준은 고체를 구성하는 원자에 의해 결정된다. 그림 1은 소자 반도체 Si의 하리송 도표를 보여준다. 왼쪽에서 오른쪽으로 s-오르비탈과 p-오르비탈 혼합은 sp33 본딩을 촉진하며, sp-Si-Si 디머가 결합되어 고체를 형성할 때 전도 및 발란스 밴드를 정의한다. 고체/진공 인터페이스의 각 원자에 있는 것과 같은 결원이 존재한다면, 그림 1과 같이 단일 자기 혼합 Si 원자의 그것과 동일한 에너지를 갖는 적어도 하나의 깨진 sp3 결합이 발생할 것이다. 이 에너지는 발랑스 밴드보다 약 0.55eV 높은 Si의 밴드갭의 중간 정도에 해당한다. 확실히 이것은 가장 이상적인 경우인 반면, 예를 들어, 결합 패시브먼트(아래 참조)와 표면 재구성이 일어난다면 상황은 달라질 것이다. 실험적으로 이러한 상태의 에너지는 예를 들어 기기 감도 및/또는 결함 밀도가 충분히 높은 경우 흡수 분광기 또는 X선 광전자 분광기를 사용하여 결정할 수 있다.
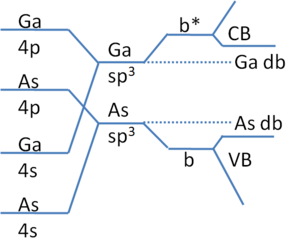
그림 2: III-IV 복합 반도체 GaAs용 해리슨 전자 에너지 다이어그램 Si와 마찬가지로, 이 크리스탈은 하이브리드화된 GaAs 조광기를 추가하여 제작된다. 공실현상은 CB 근처에 주를 형성하는 Ga Dangling 채권을 야기한다. Ga 공실은 VB 근처에 에너지를 가진 As 매달린 결합을 생산한다. VB는 이온성이 As 원자 위에 전자를 놓기 때문에 주로 "As-like" 상태로 만들어지고, 그 결과 CB 상태는 "Ga-like"이다. GaAs와 같은 복합 반도체는 밴드 가장자리에 더 가까운 결합 상태를 가지고 있다(그림 2 참조). 유대가 점점 더 이온화됨에 따라, 이러한 상태는 심지어 도펜트 역할을 할 수도 있다. 이는 높은 증기압력으로 인해 높은 Ga Dangling 본드 밀도로 인해 N 빈자리가 많은 GaN p-type 도핑이 잘 알려진 원인이다. 이러한 상태는 전도 밴드 가장자리에 가까우므로 기증자의 역할을 한다. p형 수용 도파제가 도입되면 N형 결원이 즉시 보상된다. 이러한 얕은 상태에서는 음이온 또는 양이온 공실의 경우(음이온 공실의 경우 홀 유효 질량, m*, 음이온 공실의 경우 전자 m*)와 같이 수소 원자에 대한 아날로그 처리로 간주되는 경우가 많다. 결합 에너지인 E-E는cdb

여기서 U=-q2/(4πεrr)는 ε, 자유 공간 허용도 상수, εr, 상대 허용률, r 전자-이온 코어 분리와 함께 매달린 본드와 그 이온 노심을 점유하는 전자 사이의 정전기 전위다. 전자 변환 에너지인 KE=-U/2가 단순화된 것은 중심대칭 전위에 대한 처녀적 정리 때문이다. 보어 모델에서 설명한 바와 같이, r은 정량화의 대상이 된다.
= ( ) r
전자운동량은 p=mv=h/dm 이다.

결과적으로

그리고
 .
.
이 치료는 결함이 양쪽 밴드 가장자리에서 멀어지기 때문에 정확성을 잃는다.
결함 산란
매달린 결합 에너지 수준은 결점 근처에 있는 전자를 설명하는 파동 기능의 고유값이다. 반송파 산란을 일반적으로 고려할 때, 이는 페르미의 산란 빈도 황금률의 최종 상태에 해당한다.

H'가 교호작용 파라미터이고 Dirac 델타 함수인 Δ(E-Efi)가 탄성 산란을 나타낸다. 단순한 관계 1/192= σk',k S는k'k σ = neτ2 /m* 및 다른 산란 과정을 통합하는 Matthiessen의 규칙과 함께 사용될 때 재료 운송 특성을 특성화하는 데 유용한 방정식을 만든다.
S의k'k 값은 주로 상호작용 파라미터 H'에 의해 결정된다. 이 용어는 얕은 상태를 고려하느냐 깊은 상태를 고려하느냐에 따라 다르다. 얕은 상태의 경우, H'는 다시 정의된 해밀턴 H=Ho+H'의 섭동 용어로서, H는o E의i 고유값 에너지를 갖는다. 이 사건의 매트릭스는

여기서 'k'는 결점 밀도가 밴드(~<10102/cm)를 형성하지 못할 정도로 작기 때문에 단 하나의 값만 존재하는 최종 상태 파형 벡터다. 푸리에 주기적인 점 전하를 위한 포아송 방정식을 사용하면,
{-
V가 볼륨인 매달린 본드q V=e/(qεvV2r)에서 잠재적 푸리에 계수를 제공한다. 결과적으로

여기서 q는s 충전 스크리닝으로 인한 데비 길이 파형 벡터 보정이다. 그러면 산란 주파수는
![{\displaystyle {\frac {1}{\tau }}=\sum _{{\bar {k}}',{\bar {k}}}S_{{\bar {k}}'{\bar {k}}}=n\sum _{\bar {k}}{\frac {2\pi }{\hbar }}{\frac {e^{4}\delta (E_{\bar {k}}-E_{{\bar {k}}'})}{\varepsilon \varepsilon _{r}V[{\bar {q}}^{2}-q_{s}^{2}]^{2}}}={\frac {ne^{4}}{4\pi ^{2}\hbar \varepsilon \varepsilon _{r}}}\int \int \int dkd\theta d\phi {\frac {k^{2}sin\theta \;\delta (E_{\bar {k}}-E_{{\bar {k}}'})}{[{\bar {q}}^{2}-q_{s}^{2}]^{2}}}\;\;(10)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/563dab99ccb2f8c08a1a5c2bad1979bd49e7d73b)
여기서 n은 체적 결점 밀도다. k = k' 를 활용한 통합 수행은 다음을 제공한다.
{ .
.
매달린 본드 전위는 푸리에 시리즈로 표현되기 때문에 결함이 주기적이지 않을 때 위의 치료는 흔들린다. Eq(10)의 n 계수에 의한 합계의 단순화는 결점 밀도가 낮기 때문에 가능했다. 만약 모든 원자(또는 다른 원자)가 한 개의 매달린 결합을 가지려면, 이것은 재구성되지 않은 표면에 대해 상당히 타당한 것이다. k'의 적분 또한 수행되어야 한다. 교호작용 행렬을 정의할 때 섭동 이론의 사용으로 인해, 위에서는 밴드 가장자리에 가까운 H' 또는 얕은 결함 상태의 작은 값을 가정한다. 다행히 페르미의 황금률 자체는 상당히 일반적이며 전도 전자와 결함의 상호작용을 H'를 대체하는 연산자로 모델링할 수 있을 정도로 충분히 이해한다면 깊은 상태의 결함에 사용될 수 있다.
실험측정

그림 3: (상단) 결점 밀도가 증가하는 단순 선원-배수 전압 스위프를 사용하여 반송파 산란율과 매달린 본드 에너지(결점이 더 많은 빨간색 곡선)를 추출할 수 있다. (하단) 저항성의 온도 의존성. 절대 0에 가까우면 반송파 산란에서 결함의 무게가 드러난다. 이러한 매달린 결합이 전기 운송에 미치는 정도를 결정하는 것은 실험적으로 쉽게 관찰할 수 있다. 도체(그림 3)와 저항, 그리고 정의된 지오메트리로 전압을 쓸어담음으로써 샘플의 전도도를 결정할 수 있다. 앞에서 언급한 바와 같이 σ = neτ2 /m*, 여기서 mi은 페르미 레벨 위치 및 재료 밴드 구조에서 n과 m*를 알고 결정할 수 있다. 불행히도, 이 값은 음운에 의한 것과 같은 다른 산란 메커니즘의 영향을 포함한다. 이는 그림 1/4 대 n의 경사가 E-E를cdb 계산할 수 있게 만들고 절편이 결점 산란 과정을 제외한 모든 프로세스에서 1/2을 결정하는 Eq(11)와 함께 측정했을 때 유용성을 얻는다. 이를 위해서는 음소 산란(다른 공정 중, 무시할 수 있는 공정 중)이 결함 농도와 무관하다는 가정을 필요로 한다.
비슷한 실험에서는 음소 밀도가 무시해도 될 정도로 감소하도록 도체의 온도(그림 3)만 낮출 수 있어 결함 지배 저항성이 허용된다. 이 경우 σ = neτ2 /m*을 사용하여 결점 산란을 위한 τ을 직접 계산할 수 있다.
패시브먼트

그림 4: Si/SiO2 인터페이스 상태 감소를 위한 Si 금속-산화물-반도체 전계효과 트랜지스터(MOSFET)의 수소 전달 Si에 대한 수소 결합은 결함 상태 점유율을3 제공하여 이러한 상태로 캐리어가 산란하는 것을 방지한다. 표면 결함은 전도 전자가 이러한 상태로 흩어지지 않도록 하기 위해 항상 원자와 함께 해당 에너지 수준을 의도적으로 점유할 수 있다(Eq (10)에서 효과적으로 n을 감소시킨다. 예를 들어 수소를 포함한 MOSFET의 채널/산화물 인터페이스에서의 Si 패시브레이션(그림 4)은 최대 10cm10−2 결함 밀도를 12배까지[4] 감소시켜 이동성을 향상시키고, 따라서 전환 속도를 향상시키는 전형적인 절차다. 터널링 장벽을 감소시킬 수 있는 중간 상태를 제거하면 게이트 누출 전류도 감소하고 게이트 캐패시턴스 및 과도 응답도 증가한다. 그 효과는 Si sp3 본딩이 완전히 만족되는 것이다. 여기서 분명한 요건은 반도체 전자 친화력 χ과 원자 이온화 에너지 E로I 반도체에서 통과 원자 또는 E-Ecdb + χ > E를I 산화시킬 수 있는 능력이다.
포논 산란
우리는 이제 격자 변형과 함께 포논이라고 불리는 캐리어를 산란시키는 것을 고려한다. Consider the volumetric displacement such a propagating wave produces,  , which consequently results in a time-dependent strain,
, which consequently results in a time-dependent strain,  where a simple plane wave is used to describe the phonon propagation, ( , t) e p± - i ) t
where a simple plane wave is used to describe the phonon propagation, ( , t) e p± - i ) t 원자가 평형 위치에서 멀어지면 일반적으로 전자 대역 구조에 변화가 일어나며, 여기서 산란할 경우 에너지 ~E가CB 있는 전도 대역의 전자와 관련이 있다.
원자가 평형 위치에서 멀어지면 일반적으로 전자 대역 구조에 변화가 일어나며, 여기서 산란할 경우 에너지 ~E가CB 있는 전도 대역의 전자와 관련이 있다.

경험적 매개변수 Z는DP 변형 전위라고 불리며 전자-포논 결합 강도를 설명한다. 포논 모집단에 곱하기(보스-아인슈타인 분포q, N)는 총 변형 전위를 제공한다.

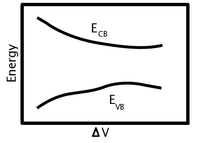
그림 5: 결정의 원자 위치가 평형에서 변위되어 체적 변형이 발생함에 따라 에너지 밴드 가장자리(전도 밴드, E 및 발란스 밴드 E )의 변경 도식 (근원의 이유는 아래에 분명히 나타날 것이다. 여기서 +는 산란 이벤트 중 음소 흡수 및 음소 방출에 해당한다. 참고: 가로 방향의 ( , t) 때문에 세로 방향의 음소와의 상호작용만 0이 아니다. 따라서 완전한 상호작용 행렬은
세로 방향의 음소와의 상호작용만 0이 아니다. 따라서 완전한 상호작용 행렬은

크론커 델타가 모멘텀 보존을 시행하고 전자파 기능(최종 상태 <  초기 인k >{\ 등도 평면파라고 가정할 때 발생한다
초기 인k >{\ 등도 평면파라고 가정할 때 발생한다
어쿠스틱 포논
페르미의 황금률을 이용하여 저에너지 음향 음소폰의 산란율을 대략적으로 추정할 수 있다. 이 음소들의 상호작용 행렬은

음핵 방사 주파수 Ωq=cq, 볼륨 V, 고밀도 ρ, 음핵 그룹 속도 c.[5] Eq에 연결하면
![{\displaystyle S_{k'k}^{Ac}={\frac {2\pi }{\hbar }}Z_{DP}^{2}{\frac {\hbar \omega _{q}}{2V\rho c^{2}}}(N_{q}+{\frac {1}{2}}\pm {\frac {1}{2}})\delta _{k',k\pm q}\delta [E(k')-E(k)\pm \hbar \omega _{q}]\;\;(16)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce4409fbb8cc02f676524c512a2c035e41876d2d)
Nq>1, Ω<<kT and g(E') ~ g(전도에너지는 일반적으로 Ω보다 훨씬 크고 g(E)에는 반 호브 특이성이 없기 때문에 일반적으로 3D 결정을 위해 보유하는) 가정에서는 산란률을 다음과 같이 가정한다.

![{\displaystyle ={\frac {2\pi }{\hbar }}Z_{DP}^{2}{\frac {\hbar \omega _{q}}{2V\rho c^{2}}}({\frac {kT}{\hbar \omega _{q}}})\sum _{k}\delta _{k',k\pm q}\delta [E(k')-E(k)\pm \hbar \omega _{q}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a16459c2d31e39a0458f4751ba9ea65e25d1f6d9)


여기서 g(E)는 포물선 분산과 함께 3차원 솔루션을 사용하여 최종 답을 얻은 상태의 전자 밀도다.
광학 포논
일반적으로 진동 분산 관계의 광학 가지에 있는 음핵은 kT 이상의 순서에 에너지를 가지므로 근사치 Ω<kT와 Nq>1을 만들 수 없다. 그러나, 복잡한 포논 분산을 처리하는 것으로부터 여전히 우회로를 제공하는 합리적인 루트는 고형분에는 단 하나의 포논 모드만이 존재한다는 것을 기술한 아인슈타인 모델을 사용하고 있다. 광학 포논의 경우 Ω(q)의 기울기 편차가 매우 적기 때문에 이 근사치가 충분한 것으로 판명되어 상수인 Ω(q) ≅ ω Ω을 주장할 수 있다. 따라서 N도q 상수(T에만 의존함)이다. 마지막 근사, g(E')=g(E±ħΩ) ~ g(E)는 ħΩ ~ E 이후 만들 수 없으며 해결 방법이 없지만 τ의 합계에 추가된 복잡성은 미미하다.
![{\displaystyle {\frac {1}{\tau }}=\sum _{k'}S_{k'k}^{Op}={\frac {2\pi }{\hbar }}Z_{DP}^{2}{\frac {\hbar \omega }{2V\rho c^{2}}}(N_{q}+{\frac {1}{2}}\pm {\frac {1}{2}})\sum _{k'}\delta _{k',k\pm q}\delta [E(k')-E(k)\pm \hbar \omega ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d40d6e190162c4856c40348d1e46e9ab5c4bf39)
 .
.
합계는 E'에서 상태 밀도로 돌아가며, 보세-아인슈타인 분포는 Ω(q) ≅ ω Ω으로 인해 합에서 뺄 수 있다.
메모들
- ^ 해리슨, 월터 A, 전자 구조 및 고체의 특성: 화학 결합의 물리학. 샌프란시스코: 프리먼, 1980년
- ^ Rocket, Angus, 반도체의 재료 과학. 뉴욕: 스프링거, 2007
- ^ Hess, Karl, 반도체 소자의 고급 이론. 뉴욕: 와일리 인터사이언스, 2000년
- ^ Faughnan, B; 입리, A. C. IEEE 트랜스. 일렉트릭 36, 101, 1999
- ^ Conwell, E. M. "반도체에서의 하이 필드 전송", 솔리드 스테이트 물리학, ed. F. 세이츠, D. 턴불, 그리고 H. 에렌레이치, 보충판 9호 뉴욕: 아카데미 프레스, 1967, 페이지 108.











![{\displaystyle {\frac {1}{\tau }}=\sum _{{\bar {k}}',{\bar {k}}}S_{{\bar {k}}'{\bar {k}}}=n\sum _{\bar {k}}{\frac {2\pi }{\hbar }}{\frac {e^{4}\delta (E_{\bar {k}}-E_{{\bar {k}}'})}{\varepsilon \varepsilon _{r}V[{\bar {q}}^{2}-q_{s}^{2}]^{2}}}={\frac {ne^{4}}{4\pi ^{2}\hbar \varepsilon \varepsilon _{r}}}\int \int \int dkd\theta d\phi {\frac {k^{2}sin\theta \;\delta (E_{\bar {k}}-E_{{\bar {k}}'})}{[{\bar {q}}^{2}-q_{s}^{2}]^{2}}}\;\;(10)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/563dab99ccb2f8c08a1a5c2bad1979bd49e7d73b)














![{\displaystyle S_{k'k}^{Ac}={\frac {2\pi }{\hbar }}Z_{DP}^{2}{\frac {\hbar \omega _{q}}{2V\rho c^{2}}}(N_{q}+{\frac {1}{2}}\pm {\frac {1}{2}})\delta _{k',k\pm q}\delta [E(k')-E(k)\pm \hbar \omega _{q}]\;\;(16)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce4409fbb8cc02f676524c512a2c035e41876d2d)

![{\displaystyle ={\frac {2\pi }{\hbar }}Z_{DP}^{2}{\frac {\hbar \omega _{q}}{2V\rho c^{2}}}({\frac {kT}{\hbar \omega _{q}}})\sum _{k}\delta _{k',k\pm q}\delta [E(k')-E(k)\pm \hbar \omega _{q}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a16459c2d31e39a0458f4751ba9ea65e25d1f6d9)


![{\displaystyle {\frac {1}{\tau }}=\sum _{k'}S_{k'k}^{Op}={\frac {2\pi }{\hbar }}Z_{DP}^{2}{\frac {\hbar \omega }{2V\rho c^{2}}}(N_{q}+{\frac {1}{2}}\pm {\frac {1}{2}})\sum _{k'}\delta _{k',k\pm q}\delta [E(k')-E(k)\pm \hbar \omega ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d40d6e190162c4856c40348d1e46e9ab5c4bf39)