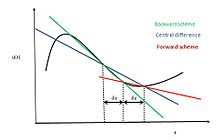
중앙 차이점 정리 방식

응용 수학에서 중심 차이점 분석 체계는 고려된 패치의 중심 노드에서 미분 연산자의 근사치를 최적화하고 미분 방정식에 대한 수치 해답을 제공하는 유한 차이 방법이다.^[1]통합 대류-확산 방정식을 해결하고 e 면과 w 면의 전송 특성 Ⅱ를 계산하기 위해 사용되는 방법 중 하나이다. 여기서 e와 w 면은 e와 w 면(composite directions는 일반적으로 계산 그리드에 대한 방향을 나타내기 위해 사용됨)이다.이 방법의 장점은 최소한 단순한 물질적 관계에 대해서는 이해와 구현이 용이하고, 정합률이 전방과 후방 차이점화 등 일부 유한한 차이점화 방법보다 빠르다는 것이다.기본적으로 확산 용어를 강조하는 대류-확산 방정식의 오른쪽은 중심차 근사치를 사용하여 나타낼 수 있다.해법과 분석을 단순화하기 위해 선형 보간법을 논리적으로 사용하여 이 방정식의 왼쪽에 대한 셀 면 값을 계산할 수 있는데, 이는 대류 항에 불과하다.따라서 균일한 그리드에 대한 특성의 셀 면 값은 다음과 같이 기록할 수 있다.^[2]

${\displaystyle \Phi \{e}=(\Phi _{P}+\Phi _{E}/2}$

${\displaystyle \Phi \{W}=(\Phi _{W}+\Phi _{P}/2}$

정상상태 대류확산식

대류-확산 방정식은 확산 및 대류 방정식의 집합적 표현이며, 물리적 시스템 내부의 입자, 에너지 및 기타 물리적 양의 전이에 대류 및 확산과 관련된 모든 물리적 현상을 설명하거나 설명한다.^[3]null

${\displaystyle \operatorname {div}(\rho u\varphi )=\operatorname {div}(\Gamma \nabla \varphi )+S_{\varphi };\,}$

...여기서 г은 확산계수, φ은 속성이다.null

정상상태 대류확산식 공식화

제어 볼륨에 대한 정상 상태 대류-증류 방정식의 공식 통합은 다음을 제공한다.

${\displaystyle \int \limits _{A}\,n\cdot (\rho u\varphi )\,dA=\int \limits _{A}\,n\cdot (\Gamma \nabla \varphi )\,dA+\int \limits _{CV}\,S_{\varphi }\,dV}$ → Equation 1.

이 방정식은 제어 부피의 플럭스 균형을 나타낸다.왼쪽은 순대류(순대류)를 주고, 오른쪽은 순확산유량(순확산유량)과 제어량 내 재산의 생성 또는 파괴를 포함한다.null

소스 항 방정식이 없을 때는 다음과 같이 된다.

${\displaystyle \frac{d}{}}$ ${\displaystyle \frac{x}{}}$ (${\displaystyle \frac{}{}\rho }$ ${\displaystyle u}$ ${\displaystyle \phi }$)${\displaystyle }$= ${\displaystyle \frac{d}{}}$ ${\displaystyle x\frac{}{}}$( d ${\displaystyle \frac{\phi }{}}$ ${\displaystyle \frac{d}{}}$ x${\displaystyle \frac{}{}}$) ${\$ $$→ 방정식 2.

연속성 방정식:

${\displaystyle \frac{d}{}}$ ${\displaystyle \frac{x}{}}$ (${\displaystyle \frac{}{}\rho }$ ${\displaystyle u}$)${\displaystyle }$= ${\displaystyle 0}$ ${\$d 디스플레이 $스타일 {$d$\over dx}(\rho u)=0}$ $$→ 방정식 3.

제어 부피를 가정하고 제어 부피 위에 방정식 2를 통합하면 다음과 같은 결과를 얻을 수 있다.

${\displaystyle (\rho u\varphi A)_{e}-(\rho u\varphi A)_{w}=(\Gamma Ad\varphi /dx)_{e}-(\Gamma Ad\varphi /dx)_{w}}$ → Integrated convection–diffusion equation

방정식 3 수율의 통합:

${\displaystyle (}$ ${\displaystyle \rho }$ ${\displaystyle u}$ A${\displaystyle {}_{}}$) ${\displaystyle e_{}}$ -${\displaystyle {}_{}}$(${\displaystyle \rho }$ ${\displaystyle u}$ A${\displaystyle {}_{}}$) ${\displaystyle w_{}}$= ${\displaystyle 0}$ ${\displaystyle (\rho uA)_{e}-(\rho uA)_{w}=0}$ $$→ 통합 연속성 방정식

단위 면적당 대류 질량 유속과 셀 면에서의 확산 전도성을 나타내는 두 가지 변수를 정의하면 편리하다.

$F=\rho u}$

$D=\감마 /\delta x}$

$A{\displaystyle {}_{}}$ ${\displaystyle e_{}}$= ${\displaystyle {}_{}}$ ${\displaystyle w_{}}$ ${\$라고 가정함$A_{w}},$ 다음과 같이 통합대류-디퓨전 방정식을 작성할 수 있다.

${\displaystyle F_{e}\varphi _{e}-F_{w}\varphi _{w}(\varphi _{E}-\varphi _{P}-D_{W})(\varphi _{P}-\varphi _{W})}$

통합 연속성 방정식은 다음과 같다.

${\displaystyle F_{e}-F_{w}=0}$

중심 차이점 분석 체계에서 대류 용어에 대한 셀 면 값을 계산하기 위해 선형 보간법을 시도한다.null

균일한 그리드의 경우, 특성 φ의 셀 면 값을 다음과 같이 쓸 수 있다.

${\displaystyle \varphi _{e}=(\varphi _{E}+\varphi _{P}/2,\quad \varphi _{w}=(\varphi _{P}+\varphi _{W}/2}$

이를 통합 대류-확산 방정식으로 대체하면서 다음을 얻는다.

${\displaystyle F_{e}{\frac {\varphi _{E}+\varphi _{P}}{2}}-F_{w}{\frac {\varphi _{W}+\varphi _{P}}{2}}=D_{e}(\varphi _{E}-\varphi _{P})-D_{w}(\varphi _{P}-\varphi _{W})}$

그리고 재배열 시:

${\displaystyle \left[\left(D_{w}+{\frac {F_{w}}{2}}\right)+\left(D_{e}-{\frac {F_{e}}{2}}\right)+(F_{e}-F_{w})\right]\varphi _{P}=\left(D_{w}+{\frac {F_{w}}{2}}\right)\varphi _{W}+\left(D_{e}-{\frac {F_{e}}{2}}\right)\varphi _{E}}$

${\displaystyle a_{P}\varphi _{P}=a_{W}\varphi _{W}+a_{E}\varphi _{E}}}}$

중앙 차이점 보관 방법의 다른 측면

보수성

노드 1과 4 주변의 제어 볼륨에 대한 경계 플럭스를 고려하여 각 제어 볼륨을 통한 순 플럭스를 합산하여 전체적인 플럭스 균형이 이루어지기 때문에 중앙 차이점화 방식에서 보존이 보장된다.null

노드 1 및 4 주변의 제어 볼륨에 대한 경계 유동성

${\displaystyle {\begin{aligned}&\left[{\frac {\Gamma _{e_{1}}(\varphi _{2}-\varphi _{1})}{\delta x}}-q_{A}\right]+\left[{\frac {\Gamma _{e_{2}}(\varphi _{3}-\varphi _{2})}{\delta x}}-{\frac {\Gamma _{w_{2}}(\varphi _{2}-\varphi _{1})}{\delta x}}\right]\\[10pt]+{}&\left[{\frac {\Gamma _{e_{3}}(\varphi _{4}-\varphi _{3})}{\delta x}}-{\frac {\Gamma _{w_{3}}(\varphi _{3}-\varphi _{2})}{\delta x}}\right]+\left[q_{B}-{\frac {\Gamma _{w_{4}}(\varphi _{4}-\varphi _{3})}{\delta x}}\right]=q_{B}-q_{A}\end{aligned}}}$

because ${\displaystyle \Gamma _{e_{1}}=\Gamma _{w_{2}},\Gamma _{e_{2}}=\Gamma _{w_{3}},\Gamma _{e_{3}}=\Gamma _{w_{4}}}$

경계성

중앙 차이점 보관 체계는 경계성의 첫 번째 조건을 만족시킨다.null

Since ${\displaystyle F_{e}-F_{w}=0}$ from continuity equation, therefore; ${\displaystyle a_{P}\varphi _{P}=a_{W}\varphi _{W}+a_{E}\varphi _{E}}$

경계성에 대한 또 다른 필수 요건은 탈부착 방정식의 모든 계수가 동일한 부호(일반적으로 모두 양성)를 가져야 한다는 것이다.단일 지향성 흐름에 맞을 때(peclet 번호)Fe/De<>2{\displaystyle F_{e}{e}<2}때문에(Fe을 하지만 이것은 오직;0, Fw>0{\displaystyle F_{e}>, 0, 만족한다.만약 De을 F_{w}>0})E)(De− Fe/2){\displaystyle a_{E}(D_{e}-F_{e}/2)}은 항상 중요하지만 Fe/긍정적이다.$[\displaystyle D_{e}]$$F_{e}/2}$

이동성

그것은 peclet 수의 크기에 따라 이동성이 변화할 것을 요구한다. 즉$,$ pe가 0일 때 $pe$가 모든 방향으로 균등하게 퍼져나가고$$ pe가 증가함에 따라$($결합 > 확산) $pe$가 증가함에 따라 $pe$가 크게 업스트림 값에 의존하며 다운스트림$값$에 덜 의존한다$.$그러나 한 지점에서 Ⅱ는 모든 Pe에 대한 인접 노드의 평균이기 때문에 중심 차이점 보관 방식은 높은 pe에서 이동성을 가지고 있지 않다.null

정확도

중앙 차이점화 계획의 테일러 시리즈 잘라내기 오류는 두 번째 순서다.중심 차등화 계획은 Pe < 2가 되어야 정확할 것이다.이러한 한계 때문에 중앙 차이점 보관 방법은 일반 목적 흐름 계산에 적합하지 않다.null

중앙 차이점 보관 방법의 적용

• 그것들은 현재 오일러 방정식과 나비에의 해법에서 정기적으로 사용되고 있다.-스토크 방정식.
• 중앙 차이점 근사치를 사용한 결과는 매끄러운 지역에서 정확도가 눈에 띄게 향상되었음을 보여주었다.
• 충격파 표현과 경계층 정의는 거친 메시에 개선될 수 있다.^[4]

이점

• 프로그래밍이 간편하고, 단계당 컴퓨터 시간이 더 적게 필요하며, 멀티그리드 가속 기법과 잘 호환됨
• 4차 분산과 연계하여 자유 매개변수를 가지며, 안정 상태에 접근하는데 필요하다.
• Peclet 번호가 2보다 작을 경우 1차 상승 방식보다 정확함.^[5]

단점들

• 다소 더 방산적인

• 국소 Peclet 수가 2보다 클 경우 용액의 진동 또는 분진으로 이어진다.^[6]

참고 항목

• 유한차법
• 유한차이
• 테일러 시리즈
• 테일러 정리
• 대류-디퓨전 방정식
• 확산
• 대류
• 페클레 수
• 선형 보간법
• 대칭파생상품
• 대류를 위한 바람의 차이점화 방식

참조

추가 읽기

• 컴퓨터 유체 역학: 응용프로그램의 기본사항 – John D.앤더슨, ISBN 0-07-001685-2
• Computing Fluid Dynamics 1권 – Claus A.호프만, 스티브 T치앙, ISBN 0-9623731-0-9

외부 링크

• 1차원_스티디-상태_컨버전스_and_디퓨전#중앙_차이_Scheme
• 유한 차이
• 중앙 차이 방법
• 포아송-네른스트-플랑크 방정식의 보수적 유한차이 계획