유한차법

이 글에는 여러 가지 문제가 있다. 이 문제를 개선하거나 대화 페이지에서 토의하십시오. (이러한 템플릿 메시지를 제거하는 방법 및 시기 알아보기) 이 글의 리드 섹션은 요점을 적절히 요약하기에는 너무 짧을 수 있다. 기사의 모든 중요 측면에 대한 액세스 가능한 개요를 제공하도록 리드를 확대하는 것을 고려하십시오(2015년 4월). 이 글은 대부분의 독자들이 이해하기에는 너무 기술적인 것일 수도 있다. 기술 세부 정보를 제거하지 않고 비전문가가 이해할 수 있도록 개선하십시오.(2015년 4월) (이 템플릿 메시지를 제거하는 방법 및 시기 학습) 이 글의 어조나 문체는 위키백과에서 사용되는 백과사전적 어조를 반영하지 못할 수도 있다. 제안사항은 위키피디아의 더 나은 기사 작성 안내서를 참조하십시오. (2020년 6월) (이 템플릿 메시지를 제거하는 방법과 시기 알아보기) (이 템플릿 메시지를 제거하는 방법 및 시기 알아보기)

미분 방정식
장애물 주위의 공기 흐름을 시뮬레이션하는 데 사용되는 Navier-Stokes 미분 방정식
범위
필드 자연과학 공학 천문학 물리학 화학 생물학 지질학 응용 수학 연속체 역학 혼돈 이론 다이너믹 시스템 사회과학 경제학 인구역학
분류
종류들 보통 부분적 차동알지브라질 인터그로 차동 분수 선형 비선형 변수 유형별 종속변수와 독립변수 자율적 콤플렉스 결합/분리됨 정확한 동종/비동종 특징들 주문 연산자 표기법
프로세스와의 관계 차이(구체 아날로그) 스토카스틱 확률적 부분 지연
해결책
존재와 고유성 피카르-린델뢰프 정리 페아노 존재 정리 카라테오도리의 존재 정리 카우치-코왈레프스키 정리
일반 주제 룬스키안 위상 초상화 위상공간 랴푸노프 / 점근증 / 지수 안정성 수렴율 시리즈/적분 솔루션 수치적 통합 디라크 델타 함수
솔루션 방법 감사 특성방법 오일러 지수 반응식 유한차이 (크랭크-니콜슨) 유한요소 무한요소 유한 부피 갤러킨 페트로프-갈러킨 집적인자 적분 변환 섭동 이론 룬게쿠타 변수의 분리 결정되지 않은 계수 모수의 변동
사람
리스트 아이작 뉴턴 고트프리드 라이프니즈 레온하르트 오일러 에밀 피카르 요제프 마리아 회네브로이스키 에른스트 린델뢰프 루돌프 립시츠 아우구스틴루이코치 존 크랭크 필리스 니콜슨 칼 데이비드 톨메 룬지 마르틴 쿠타
v t

수치해석에서는 유한차이 방법(FDM)이 유한차이 유도체를 근사하여 미분방정식을 푸는 수학적 기법의 한 종류다. 공간 영역과 시간 간격(해당되는 경우) 모두 디스코트되거나 한정된 수의 스텝으로 분할되며, 이 이산형 지점에서의 해답 값은 인근 지점으로부터 유한 차이와 값을 포함하는 대수 방정식을 풀어서 근사치를 구한다.

유한차법은 비선형일 수 있는 일반미분방정식(OSE)이나 부분미분방정식(PDE)을 매트릭스 대수기법으로 해결할 수 있는 선형방정식으로 변환한다. 현대 컴퓨터는 이러한 선형 대수 계산을 효율적으로 수행할 수 있으며, 이는 구현의 상대적 용이성과 함께 현대적 수치 해석에서 FDM을 널리 사용하게 했다.^[1] 오늘날, FDM은 유한 요소 방법과 함께 PDE의 수치 해법에 대한 가장 일반적인 접근방식 중 하나이다.^[1]

테일러의 다항식에서의 파생

첫째, 파생상품의 근사치를 추정할 함수가 적절한 행동이라고 가정하면, 테일러의 정리를 통해 테일러 시리즈 확장을 만들 수 있다.

${\displaystyle f(x_{0}+h)=f(x_{0})+{\frac {f'(x_{0}){1!}}}h+{\frac {f^{(2)}(x_{0}){2!}}}h^{2}+\cdots +{\frac {f^{(n)}(x_{0}){n!}}}h^{n}+R_{n}(x),}$

여기서 n!은 n의 요인을 나타내며, R_n(x)는 나머지 기간으로, diecond n의 Taylor 다항식과 원래 함수 사이의 차이를 나타낸다. Taylor 다항식을 먼저 잘라냄으로써 함수 "f"의 첫 번째 파생상품에 대한 근사치를 도출할 것이다.

${\displaystyle f(x_{0}+h)=f(x_{0})+f'(x_{0}h+R_{1}(x),}$

설정, x₀=a 우리가 가지고 있는,

${\displaystyle f(a+h)=f(a)+f'(a)h+R_{1}(x),}$

h로 나누면 다음과 같은 장점이 있다.

${\displaystyle {f(a+h) \over h}={f(a) \over h}+f'(a)+{R_{1}(x) \over h}}}}}$

f'(a):

${\displaystyle f'(a)={f(a+h)-f(a) \over h}-{R_{1}(x) \over h}}}}$

$R{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$( ${\displaystyle x}$) ${\displaystyle R_{1}(x)}$이(가) 충분히$$ 작다고 가정하면, "f"의 첫 번째 파생상품의 근사치는 다음과 같다.

${\displaystyle f'(a)\cHB(a+h)-f(a) \over h}.}$

이는 우연치 않게 다음과 같이 주어지는 파생상품의 정의와 유사하다.

${\displaystyle f'(a)=\lim _{h\to 0}{\frac {f(a+h)-f(a){h}}.}$

0을 향한 한계를 제외하고(방법은 이 이름을 따서 명명한다).

정확도 및 순서

방법의 해답의 오차는 근사치 및 정확한 분석 해답의 차이로 정의된다. 유한차이의 방법에서 두 가지 오차는 반올림 오차, 십진수량의 컴퓨터 반올림으로 인한 정밀도의 상실, 잘림 오차 또는 탈소화 오류, 원래의 미분 방정식의 정확한 해법과 완벽한 산수를 가정하는 정확한 수량의 차이(즉, 반올림이 없다고 가정함)이다.-off).

문제에 대한 해답의 근사치를 위해 유한 차이 방법을 사용하려면 먼저 문제의 영역을 불명확화해야 한다. 이는 대개 도메인을 균일한 그리드로 나누는 방식으로 이루어진다(오른쪽 이미지 참조). 이것은 유한 차이 방법이 종종 "시간 스텝" 방식으로 파생상품에 대한 이산형 수치 근사치를 산출한다는 것을 의미한다.

일반적인 관심의 표현은 메서드의 국소 절단 오류다. 일반적으로 Big-O 표기법을 사용하여 표현되는 로컬 잘라내기 오류는 메서드의 단일 적용에서 발생하는 오류를 가리킨다. 즉, $f{\displaystyle {}^{}}$ ${\displaystyle {\prime }^{}}$(${\displaystyle }$${\displaystyle {}_{}}$ ${\displaystyle i_{}}$) -${\displaystyle f_{}^{}}$ ${\displaystyle {}_{}^{}}$ ${\displaystyle {}_{}^{}}$ ${\$ f$'($${\displaystyle {x\_}_{}}$${i$$}-$$f'_{i}}}$이$(가$) 숫자 근사치에 대한$$ 정확한 $값$과 f${\displaystyle {}_i^{}}${\$displaystyle f'_${i$}}}$을(를) 참조할$$ 경우$$ $수량$이다. 테일러 다항식의 나머지 기간은 국소 절단 오류를 분석하는 데 편리하다. $F{\displaystyle ({}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$+ ${\displaystyle h}$) ${\displaystyle f(x_{0}+h)$에 대해 Taylor 다항식의 나머지 라그랑주 형식 사용$.$

${\$$}}}^{n+1$ 여기서 < < x 0+ {\$displaystyle x_{0}<\xi <x_{$0}+$h$

국소 절단 오류의 주요 용어를 찾을 수 있다. 예를 들어, $f{\displaystyle }$( ${\displaystyle {}_{}}$ ${\displaystyle i_{}}$)${\displaystyle }$= ${\displaystyle f}$( ${\displaystyle {x\mathrm{}}_{}}$ 0${\displaystyle {}_{}}$+ ${\displaystyle i}$ ${\displaystyle h}$) ${\displaystyle f(x_{i}}=f(x_{0}+ih$

${\displaystyle f(x_{0}+ih)=f(x_{0})+f'(x_{0}}ih+{\frac {f"(\xi )}{2!}}}}(ih)^{2},}$

그리고 대수학적 조작으로 인해

${\displaystyle {\f(x_{0}+ih)-f(x_{0})-{ih}{ih}}{ih}}}}{ih}=f'(x_{0})+{\frac {f"(\xi ){2!}}ih,}$

또한 왼쪽의 수량은 유한 차이 방법의 근사치이며, 오른쪽의 수량은 정확한 관심 수량에 나머지 수량을 더한 것이며, 나머지는 국부 절단 오류라는 것을 분명히 알 수 있다. 이 예와 그 순서의 최종 표현은 다음과 같다.

${\displaystyle {\frac {f(x_{0}+ih)-f(x_{0}}}{ih}}{ih}=f'(x_{0})+O(h).}$

즉, 이 경우 국소 절단 오류가 단계 크기에 비례한다는 것을 의미한다. 시뮬레이션된 FDM 솔루션의 품질 및 지속시간은 탈부착 방정식 선택과 단계 크기(시간 및 공간 단계)에 따라 달라진다. 데이터 품질과 시뮬레이션 기간은 단계 크기가 작을수록 크게 증가한다.^[2] 따라서, 데이터 품질과 시뮬레이션 기간 사이의 합리적인 균형은 실용화를 위해 필요하다. 대규모 시간 단계는 실제 시뮬레이션 속도를 높이는 데 유용하다. 그러나 너무 큰 시간 단계는 불안정을 야기할 수 있고 데이터 품질에 영향을 미칠 수 있다.^[3][4]

폰 노이만과 쿠란트 프리드리히스 르위 기준은 종종 수치 모델 안정성을 결정하기 위해 평가된다.^[3][4][5][6]

예제: 일반 미분 방정식

예를 들어, 일반적인 미분 방정식을 고려하십시오.

${\displaystyle u'=3u(x)+2.\,}$

이 방정식을 해결하기 위한 오일러 방법은 유한 차이 인수를 사용한다.

${\displaystyle {\frac {u(x+h)-u(x)}{h}\ch}problem u'(x)}$

먼저 u'(x)로 대체한 다음 약간의 대수학(양면을 h로 나눈 다음, 양쪽에 u(x)를 추가하여 미분 방정식을 대략적으로 계산한다.

${\displaystyle u(x+h)=u(x)+h(3u(x)+2)).\,}$

마지막 방정식은 유한차 방정식이며, 이 방정식을 풀면 미분 방정식에 대한 대략적인 해법이 나온다.

예: 열 방정식

균일한 디리클레 경계 조건의 정규화된 열 방정식을 한 차원 고려

${\displaystyle U_{t}=U_{xx}\,}$

${\displaystyle U}$( ${\displaystyle 0}$, t${\displaystyle }$)${\displaystyle }$= ${\displaystyle U}$( ${\displaystyle 1}$,${\displaystyle }$t${\displaystyle }$)${\displaystyle }$= ${\displaystyle 0}$ ${\$U(0$,t)=U$(1$,t)=0\,}($경계 조건)

${\$$U_{0}(x)\,}($초기 조건)

이 방정식을 수치로 푸는 한 가지 방법은 유한차이에 의해 모든 파생상품의 근사치를 구하는 것이다. 메쉬 $x{\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$. .${\displaystyle }$. . . . . ${\displaystyle x_{}}$ J ${\$를 사용하여 공간 내 도메인을 분할하고, 시간 내에 메쉬 $t{\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$. .${\displaystyle }$. . ${\displaystyle t_{}}$ N ${\$}, ....,$t_{N}$를 사용하여 공간 내 영역을 분할한다$.$ 공간과 시간 내 균일한 분할을 가정하므로 연속된 두 지점의 차이는 h와 con이 될 것이다.에코 타임 포인트는 k가 될 것이다. 포인트

${\displaystyle u(x_{j},t_{n}=u_{j}^{n}}}}$

$u{\displaystyle ({}_{}}$ ${\displaystyle j_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle n_{}}$)의 숫자 근사치를 나타낸다${\displaystyle .}$ ${\displaystyle u(x_{j},t_{n}).$$}$

명시적 방법

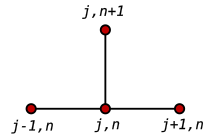
${\displaystyle {시간}_{}}$ $t{\displaystyle {}_{}}$ ${\$의 전방 차이와 위치 $x{\displaystyle {}_{}}$ ${\displaystyle j_{}}$ ${\$FTCS)에서 공간 파생 모델의 2차 중심 차이를 사용하여 다음과 같은 반복 방정식을 얻는다.

${\displaystyle {\frac {u_{j}^{n+1}-u_{j}^{n}}{k}}={\frac {u_{j+1}^{n}-2u_{j}^{n}+u_{j-1}^{h^{n}}}}}}}{h^{2}}.\,}$

이것은 1차원 열 방정식을 풀기 위한 명시적인 방법이다.

다음과 같은 ${\displaystyle {}_{}^{}}$으로 $u{\displaystyle {}_{\mathrm{j}}^{}}$ n$$+ 1 {\$displaystyle u_{$j}^{$n+1$}을$($를) 다른 값에서$$ 얻을 수 있다.

${\displaystyle u_{j}^{n+1}=(1-2r)u_{j}^{n}+ru_{j-1}^{n}+ru_{j+1}^{n}}}}}}$

여기서 $r{\displaystyle }$= ${\displaystyle k}$/ ${\displaystyle h{}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$. ${\displaystyle r=k/h^{2}.$$}$

따라서 이러한 반복 관계를 가지고, 그리고 시간 n의 값을 알면, n+1 시간에 상응하는 값을 얻을 수 있다. ${\displaystyle u_{}^{}}$ ${\displaystyle {0\mathrm{}}_{}^{}}$ ${\displaystyle {}_{}^{}}$ ${\$ 및$$ ${\displaystyle u_{}^{}}$ ${\displaystyle {}_{}^{}}$ ${\$은(는) 경계 조건으로 대체해야 하며$$, 이 예에서는 둘 다 0이다.

이 명시적 방법은 $r{\displaystyle }$ ${\displaystyle \le }$ ${\displaystyle 1}$/ ${\displaystyle 2\mathrm{}}$ ${\displaystyle r\leq$1$/2}$이(가) 있을 때마다 수치로 안정되고 수렴되는 것으로 알려져 있다$.$^[7] 숫자 오류는 시간 단계와 공간 단계의 제곱에 비례한다.

$[\displaystyle \Delta u=O(k)+]O(h^{2})\,}$

암묵적 방법

시간 $t{\displaystyle {}_{}}$ + ${\displaystyle 1_{}}$ $디스플레이$ 스타일 $t_{n+1}$의 후진 차이를 사용하고 위치$$ $x{\displaystyle {}_{}}$ ${\displaystyle j_{}}$ ${\$후진 시간, 중심 공간 방법 "BTCS")에서 공간 파생 모델에 대해 2차 중심 차이를 사용하면 다음과 같은 반복 방정식을 얻을 수 있다.

${\displaystyle {\frac {u_{j}^{n+1}-u_{j}^{n}}}{k}}={\frac {u_{j+1}-1}^{n+1}-1}^{n+1}{j-1}^{h^{n-1}.},},},}$

이것은 1차원 열 방정식을 풀기 위한 암묵적인 방법이다.

${\displaystyle {\mathrm{선형}}_{}^{}}$ 방정식의 시스템을 풀어서$$ ${\displaystyle {uj}_{}^{}}$ ${\displaystyle {}_{}^{}}$+ 1 ${\$를 얻을 수 있다.

${\displaystyle (1+2r)u_{j}^{n+1}-ru_{j-1}^{n+1}-ru_{j+1}^{n+1}=u_{j}^{n}}}}}}}}$

이 계획은 항상 숫자적으로 안정적이고 수렴적이지만, 일반적으로 각 시간 단계에서 숫자 방정식의 시스템을 해결해야 하기 때문에 명시적 방법보다 더 수적으로 집약적이다. 오류는 시간 단계에서는 선형이고 공간 단계에서는 이차적이다.

$[\displaystyle \Delta u=O(k)+]O(h^{2}).\,}$

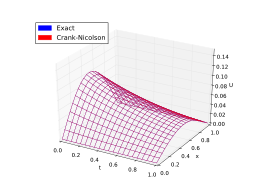
크랭크-니콜슨법

${\displaystyle {마지막}_{}}$으로 $t{\displaystyle {}_{}}$ +${\displaystyle 1_{}}$/ ${\displaystyle {2\mathrm{}}_{}}$ ${\$시의$$ 중심 차이와 위치 x j ${\$CTCS")에서 공간 파생 모델에 대한 2차 중심 차이를 사용하면 다음과 같은 반복 방정식을 얻을 수 있다.

${\displaystyle {\frac {u_{j}^{n+1}-u_{j}^{n}}{k}}={\frac {1}{2}}\left({\frac {u_{j+1}^{n+1}-2u_{j}^{n+1}+u_{j-1}^{n+1}}{h^{2}}}+{\frac {u_{j+1}^{n}-2u_{j}^{n}+u_{j-1}^{n}}{h^{2}}}\right).\,}$

이 공식은 크랭크-니콜슨 방식으로 알려져 있다.

${\displaystyle {\mathrm{선형}}_{}^{}}$ 방정식의 시스템을 풀어서$$ ${\displaystyle {uj}_{}^{}}$ ${\displaystyle {}_{}^{}}$+ 1 ${\$를 얻을 수 있다.

${\displaystyle (2+2r)u_{j}^{n+1}-ru_{j-1}-ru_{n+1}-ru_{j+1}^{n+1}=(2-2r){j}^{n}+ru_{n1}^{n}+ru_{j+1}^{n}{n}}}}}}}}:{n}}}}}}}}}}}}}}}}}}}}}}}}}:{n}:{n}^{j+ru+1}^{n}^{n}$

이 계획은 항상 수적으로 안정적이고 수렴적이지만, 보통 각 시간 단계에서 숫자 방정식의 시스템을 해결해야 하기 때문에 더 수적으로 집약적이다. 오류는 시간 단계와 공간 단계에 걸쳐 2차적으로 나타난다.

${\displaystyle \Delta u=O(k^{2})+O(h^{2}).\,}$

비교

요약하자면, 일반적으로 크랭크-니콜슨 체계는 작은 시간 단계를 위한 가장 정확한 체계다. 더 큰 시간 단계에서 암묵적 체계는 계산적으로 덜 요구되기 때문에 더 잘 작동한다. 명시적 계획은 가장 정확하지 않고 불안정할 수 있지만 또한 가장 구현하기 쉽고 수치적으로도 가장 덜 집약적이다.

여기 예가 있다. 아래 그림은 열 방정식의 근사치를 위해 위의 방법에 의해 주어진 해결책을 제시한다.

${\displaystyle U_{t}=\alpha U_{xx},\quad \alpha ={\frac {1}{\pi ^{2}}},$

경계조건으로

$[\displaystyle U(0,t)=U(1,t)=0]}$

정확한 해결책은

${\displaystyle U(x,t)={\frac {1}{\pi ^{2}}:e^{-t}\sin(\pi x)}$

예: 라플라스 연산자

$n{\displaystyle }$ ${\displaystyle n}$ -dimension의$$ (연속) Laplace 연산자는 ${\displaystyle \mathrm{\Delta u}(}$ ${\displaystyle x}$)${\displaystyle }$=${\displaystyle \underset{}{\overset{}{}}}$ ${\displaystyle \underset{}{\overset{}{}}{\mathrm{}}_{}^{}}$ ${\displaystyle \underset{}{\overset{}{i}}}$ ${\displaystyle {\mathrm{}}_{}^{}}$ ${\displaystyle {}_{}^{}(x}$) ${\delta u(x)=\sum _{i=1}^{n}\partial _{i}^{$2}$u(x)$에 의해 주어진다$.$ 이산 Laplace 연산자 $\Delta {\displaystyle {\mathrm{}}_{}}$ ${\displaystyle h_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle \Delta _{h}u}$는 치수 $n{\displaystyle }$ ${\displaystyle n}$에 따라$$ 달라진다$.$

1D에서 라플라스 연산자는 다음과 같이 근사치된다.

${\displaystyle \Delta u(x)=u'(x)\약간 {\frac {u(x-h)-2u(x)+u(x+h)}{h^{2}}=:\Delta _{h}u(x)\,}$

이 근사치는 보통 다음 스텐실을 통해 표현된다.

${\displaystyle \Delta_{h}={\frac {1}{h^{2}}:{\begin{bmatrix}1&-2&1\end{bmatrix}}}}$

대칭, 삼지각 행렬을 나타내는 거야 등거리 그리드의 경우 토우플리츠 매트릭스를 얻는다.

2D 케이스는 보다 일반적인 nD 케이스의 모든 특징을 보여준다. 각 두 번째 부분파생물은 1D 사례와 유사하게 근사하게 추정되어야 한다.

${\displaystyle {\begin{aigned}\Delta u(x,y)&=u_{xx}(x,y)+u(x,y)\\\\\precan {u(x-h,y)-2u(x,y)+u(x+h,y)}{h^{2}}}+{\frac {u(x,y-h)-2u(x,y)+u(x,y+h)}{h^{2}}}\\&={\frac {u(x-h,y)+u(x+h,y)-4u(x,y)+u(x,y-h)+u(x,y+h)}{h^{2}}}\\&=:\Delta _{h}u(x,y)\...\end{aigned}}}$

보통 다음 스텐실로 주어지는 것

${\displaystyle \Delta_{h}={\frac {1}{h^{2}}:{\begin{bmatrix}&1\1&-4&1\&1\end{bmatrix}}\,\,}$

일관성

위에서 언급한 근사치의 ${\displaystyle \mathrm{일관성}}$은$u{\displaystyle }$ ${\displaystyle \in }$ C $Ω$ ) {\$displaystyle u\$in C^{4}(\$Oomega )}$와 같은 매우 정기적인 기능에 대해 나타낼 수 있다$.$ 진술은 다음과 같다.

${\displaystyle \Delta u-\Delta _{h}u={\mathcal{O}}(h^{2})\,}$

이를 증명하기 위해서는 테일러 시리즈 증설부터 분리형 라플라스 사업자에 대한 주문 3까지 대체해야 한다.

특성.

부화음

연속 하위 고조파 함수와 유사하게 유한차 근사치 ${\displaystyle u_{}}$ h ${\$에 대한 하위 고조파 함수를 정의할 수 있다.

${\displaystyle -\Delta _{h}\leq 0\,.}$

평균값

다음을 통해 양성의 일반 스텐실을 정의할 수 있다.

${\displaystyle {\begin{bmatrix}&\alpha _{N}\\\alpha _{W}&-\alpha _{C}&\alpha _{E}\\&\alpha _{S}\end{bmatrix}}\,,\quad \alpha _{i}>0\,,\quad \alpha _{C}=\sum _{i\in \{N,E,S,W\}}\alpha _{i}\,.}$

$u{\displaystyle {}_{}}$ ${\displaystyle h_{}}$ ${\$이(가) 하위 고조파인$$ 경우 다음 평균 값 속성이 유지됨

${\displaystyle u_{h}(x_{C})\leq {\frac {\sum \{n,E,S,W\}}}\알파 _{i}u(x_{i})}{{\sum _{i\in \{N,E,S,W\}}\알파 _{i}}}$

여기서 근사치는 격자의 지점에서 평가되며, 스텐실은 양의 유형으로 가정한다.

유사한 평균값 속성도 연속 사례에 대해 유지된다.

최대 원리

a (분리) 하위 고조파 함수 ${\displaystyle u_{}}$ h ${\$의 경우 다음이$$ 유지됨

${\displaystyle \max_{h}\leq \max_{\partial \max_{h}{h}}$

여기서$\Omega {\displaystyle {\mathrm{}}_{}}$ ${\displaystyle h_{}}$ ,${\displaystyle {}_{}\mathrm{\partial }}$ ${\displaystyle {\mathrm{}}_{}}$ h ,$$∂ Ω ${\displaystyle h_{}}$ {\$displaystyle \Oomega _{h$},\partial \$Oomega }$의 경계 각각$$$\partial {\displaystyle \mathrm{}}$ ${\displaystyle \mathrm{\Omega }}$ ${\displaystyle \partial \Oomega$}의 연속 도메인 디스켓화$.$

유사한 최대 원칙도 연속적인 경우를 지탱한다.

SBP-SAT 방법

SBP-SAT 방법은 고차 유한차이를 이용하여 잘 다듬어진 부분미분방식의 경계조건의 변별 및 부과에 대한 안정적이고 정확한 기법이다.^[8][9] 이 방법은 분화 연산자가 부품별 종합 특성을 나타내는 유한한 차이에 기초한다. 일반적으로 이러한 연산자는 내부의 중앙 차이 스텐실을 갖는 분화 매트릭스와 이산형 설정에서 부품별 통합을 모방하도록 설계된 신중하게 선택된 단측 경계 스텐실로 구성된다. SAT 기법을 사용하여, 경계 값이 정확히 충족되지 않고 원하는 조건을 향해 "끌어진다"는 PSDE의 경계 조건을 약하게 부과한다. 튜닝 매개변수(SAT 기법에 부합하는)를 적절하게 선택하면, OSE의 결과 시스템은 연속적인 PDE와 유사한 에너지 동작을 보일 것이다. 즉, 시스템은 비물리적 에너지 성장성이 없다. 이는 4차 순서 런지-쿠타 방법과 같이 가상 축의 일부를 포함하는 안정성 영역과의 통합 방식을 사용할 경우 안정성을 보장한다. 이는 예를 들어 고차 분화 연산자를 사용할 경우 일반적으로 안정성이 떨어지는 주입 방식과 대조적으로 SAT 기법을 고차 유한 차이 방법에 대해 경계 조건을 부과하는 매력적인 방법으로 만든다.

참고 항목

참조

추가 읽기

• K.W. 모튼과 D.F. 메이어스, 부분 미분방정식의 수치해결, 소개 케임브리지 대학 출판부, 2005.
• 카와 에 오토타르. Eric Kalu, 응용 프로그램을 사용한 수치 방법, (2008) [1]. 08.07장의 FDM(ODE의 경우)에 대한 간략한 엔지니어링 중심 소개 포함.
• John Strikwerda (2004). Finite Difference Schemes and Partial Differential Equations (2nd ed.). SIAM. ISBN 978-0-89871-639-9.
• Smith, G. D. (1985), Numerical Solution of Partial Differential Equations: Finite Difference Methods, 3rd ed., Oxford University Press
• Peter Olver (2013). Introduction to Partial Differential Equations. Springer. Chapter 5: Finite differences. ISBN 978-3-319-02099-0..
• Randall J. LeVeque, SIAM, 2007, 일반 및 부분 미분 방정식의 유한 차이 방법.
• 세르게이 레메셰프스키, 피오트르 마투스, 드미트리 폴리아코프(Eds): "정확한 유한차이 계획", 드 그루터(2016년) DOI: https://doi.org/10.1515/9783110491326.