촘스키 정상형

공식 언어 이론에서 문맥이 없는 문법 G는 모든 생성 규칙이 다음과 같은 형태일 경우 촘스키 정규 형태(노암 촘스키에 의해 처음 기술됨)^[1]라고 합니다.^[2]^[3]

A → BC, 또는

A → a, 또는

S → ε,

여기서, A, B, C는 비말단 기호이고, 문자 a는 터미널 기호(일정한 값을 나타내는 기호)이고, S는 시작 기호이고, ε은 빈 문자열입니다.또한, B와 C 둘 다 시작 기호가 될 수 없고, 세 번째 생성 규칙은 문맥 자유 문법 G에 의해 생성된 언어인 L(G)에 ε가 있을 경우에만 나타날 수 있습니다.

Chomsky normal 형태의 모든 문법은 문맥 자유형이며, 반대로 문맥 자유형 문법은 Chomsky normal 형태의 문법과 동등한 것으로^{[note 1]} 변형될 수 있으며, 이는 원래 문법의 크기의 제곱보다 크지 않은 크기입니다.

문법을 Chomsky 정규 형태로 변환

문법을 Chomsky 정규 형태로 변환하기 위해, 일련의 간단한 변환들이 특정한 순서로 적용됩니다; 이것은 오토마타 이론에 관한 대부분의 교과서들에서 설명됩니다.^[4]^{: 87–94}^[5]^[6]^[7]이 프레젠테이션은 Hopcroft, Ullman(1979)을 따르지만 Lange, Lei ß(2009)의 변환 이름을 사용하도록 각색되었습니다.다음 각 변환은 Chomsky 정규 형태에 필요한 속성 중 하나를 설정합니다.

시작: 오른쪽에서 시작 기호를 제거합니다.

새로운 시작 기호 S와₀ 새로운 규칙을 소개합니다.

S → S,

여기서 S는 이전 시작 기호입니다.이것은 문법의 생성된 언어를 바꾸지 않으며, S는₀ 어떤 규칙의 오른쪽에도 발생하지 않습니다.

용어: 단독 터미널이 없는 규칙 제거

각 규칙을 제거하려면 다음과 같이 하십시오.

A → X ... A ... X

단말기 기호 a가 오른쪽에 있는 유일한 기호가 아닌 경우, 모든 그러한 단말기에 대해 새로운 비단말기 기호 N 및_a 새로운 규칙을 도입합니다.

N → a.

모든 규칙 변경

A → X ... A ... X

로.

A → X...N_a... X_n.

여러 개의 단자 기호가 오른쪽에 있는 경우, 각 단자 기호를 관련된 비단자 기호로 동시에 바꿉니다.이것은 문법이 만들어내는 언어를 바꾸지 않습니다.^[4]^{: 92}

BIN: 2개 이상의 단자가 있는 우측면 제거

각 규칙 바꾸기

A → X X ... X

규칙에 따라 2개 이상의 비단자₁ X,...,X를_n 사용합니다.

A → XA,

... ,

A → X X X,

여기서 A는_i 새로운 비단자 기호입니다.다시 말하지만, 이것은 문법이 만들어내는 언어를 바꾸지 않습니다.^[4]^{: 93}

DEL: ε 규칙 제거

ε 규칙은 형식의 규칙입니다.

A → ε,

여기서 A는 문법의 시작 기호인 S가₀ 아닙니다.

이 형식의 모든 규칙을 제거하려면 먼저 ε를 유도하는 모든 비단자의 집합을 결정합니다.Hopcroft와 Ullman(1979)은 이러한 비말단을 널블(nullable)이라 부르며 다음과 같이 계산합니다.

규칙 A → ε이(가) 존재하면 A는 null이 됩니다.
규칙 A → X이면...X가_n 존재하고, 모든 X가_i null이고, A도 null입니다.

각 규칙을 대체하여 중간 문법을 구합니다.

A → X ... X

일부 nullable X가_i 생략된 모든 버전에 의해.이 문법에서 각 ε 규칙을 삭제하면 왼쪽이 시작 기호가 아닌 한 변환된 문법을 얻을 수 있습니다.

예를 들어, 다음 문법에서 시작 기호 S와₀ 함께,

S → AbBC

B → AA AC

C → bc

A → a → a

비말단 A, 그리고 따라서 B는 null이고, C와 S는₀ null입니다.따라서 다음과 같은 중간 문법이 얻어집니다.^{[note 3]}

S → AbB AbB ~~AbB~~ ~~AbB~~ BC

B → AA AA AA A ε AA AC AC

C → bc

A → a → a

이 문법에서 모든 ε 규칙은 "통화 장소에서 인라인"으로 표시됩니다.다음 단계에서는 이를 삭제하여 문법을 산출할 수 있습니다.

S → AbB AbB BC

B → AA AA AC

C → bc

A → a

이 문법은 원래 예시문법인 viz와 같은 언어를 만들어냅니다.{ab,aba,abaa,aba,abbac,abb,abc,b,bab,bac,bb,bc,c}이지만 ε-rules가 없습니다.

유닛: 유닛 규칙 제거

단위 규칙은 형식의 규칙입니다.

A → B,

여기서 A, B는 비말단 기호입니다.각 규칙에 대해 제거하려면

B → X ... X,

X가₁...X는_n 터미널과 터미널이 아닌 문자열입니다. 규칙 추가

A → X ... X

이 규칙이 이미 제거(또는 제거)된 단위 규칙이 아닌 경우.결과 문법에서 비말단 기호 B의 건너뛰기는 비말단 기호 A의 단위 닫힘의 구성원이기 때문에 가능합니다.^[9]

변환순서

상호보존
변환 결과의
Y X	START	용어	BIN	DEL	구성 단위
변환 X는 항상 보존(Y)합니다. 응답은 Y의 결과를 파괴(N)할 수 있습니다.
START
용어
BIN
DEL
구성 단위				(Y)^*
^*UNIT는 DEL의 결과를 보존합니다. 이전에 START가 호출된 적이 있는 경우.

위의 변환을 적용할 순서를 선택할 때, 일부 변환은 다른 변환에 의해 달성된 결과를 파괴할 수 있음을 고려해야 합니다.예를 들어 START는 UNIT 다음에 적용될 경우 UNIT 규칙을 다시 도입합니다.표에는 어떤 주문이 허용되는지 나와 있습니다.

또한 문법 크기의^{[note 5]} 최악의 팽만감은 변환 순서에 따라 달라집니다.G를 사용하여 원래 문법 G의 크기를 나타내면, 최악의 경우에 블로우업의 크기는 사용되는 변환 알고리즘에 따라 G에서 2까지^{2 G} 다양할 수 있습니다.^[8]^{: 7}문법 크기의 블로업은 DEL과 BIN 사이의 순서에 따라 달라집니다.DEL을 먼저 수행하면 지수 함수가 될 수 있지만 그렇지 않으면 선형입니다.UNIT는 문법의 크기에 2차 블로업을 발생시킬 수 있습니다.^[8]^{: 5}START, TERM, BIN, DEL, UNIT 및 START, BIN, DEL, UNIT, TERM 순서는 최소(즉, 2차) 블로우업으로 이어집니다.

예

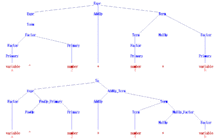
다음 문법은 시작 기호 Expr과 함께 C 또는 Algol60과 같은 프로그래밍 언어의 모든 구문 유효 산술 표현 집합의 단순화된 버전을 설명합니다.컴파일러 프론트엔드에서 내부 구조는 파서에 의해 고려되지 않기 때문에 단순화를 위해 숫자와 변수는 모두 터미널 기호로 간주됩니다.Algol60에서, 터미널 기호 "^"은 지수화를 나타냅니다.

Expr	→ 기간	Expr AddOp 용어	AddOp 용어
용어	→ 인자	용어 멀옵 인자
인자	→ 1차	요인 ^ 1차
기본적인	→ 수를	변수	(Expr)
AddOp	→ +	−
멀옵	→ *	/

위 변환 알고리즘의 START 단계에서는 문법에 규칙 S→Expr만 추가됩니다.TERM 단계 후 문법은 다음과 같습니다.

S₀	→ Expr
Expr	→ 기간	Expr AddOp 용어	AddOp 용어
용어	→ 인자	용어 멀옵 인자
인자	→ 1차	인자 파워옵 기본적인
기본적인	→ 수를	변수	열다. Expr 가까운.
AddOp	→ +	−
멀옵	→ *	/
파워옵	→ ^
열다.	→ (
가까운.	→ )

"BIN" 단계를 마치면 다음과 같은 문법을 얻습니다.

S₀	→ Expr
Expr	→ 기간	Expr 추가Op_항	AddOp 용어
용어	→ 인자	용어 MulOp_Factor
인자	→ 1차	인자 PowerOp_Primary
기본적인	→ 수를	변수	열다. Expr_닫기
AddOp	→ +	−
멀옵	→ *	/
파워옵	→ ^
열다.	→ (
가까운.	→ )
추가Op_항	→ 작업항 추가
MulOp_Factor	→ 멀옵 팩터
PowerOp_Primary	→ 파워옵 프라이머리
Expr_닫기	→ 익스프러

ε 규칙이 없으므로 "DEL" 단계에서는 문법이 변경되지 않습니다."UNIT" 단계 이후에, Chomsky 정규 형태로 다음과 같은 문법을 얻습니다.

S₀	→ 수를	변수	열다. Expr_닫기	인자 PowerOp_Primary	용어 MulOp_Factor	Expr 추가Op_항	AddOp 용어
Expr	→ 수를	변수	열다. Expr_닫기	인자 PowerOp_Primary	용어 MulOp_Factor	Expr 추가Op_항	AddOp 용어
용어	→ 수를	변수	열다. Expr_닫기	인자 PowerOp_Primary	용어 MulOp_Factor
인자	→ 수를	변수	열다. Expr_닫기	인자 PowerOp_Primary
기본적인	→ 수를	변수	열다. Expr_닫기
AddOp	→ +	−
멀옵	→ *	/
파워옵	→ ^
열다.	→ (
가까운.	→ )
추가Op_항	→ 작업항 추가
MulOp_Factor	→ 멀옵 팩터
PowerOp_Primary	→ 파워옵 프라이머리
Expr_닫기	→ 익스프러

TERM 단계에서 소개하는 N은_a PowOp, Open, Close 입니다."BIN" 단계에서 소개하는 A는_i AddOp_Term, MulOp_Factor, PowOp_Primary, Expr_Close입니다.

대체정의

촘스키 축소형

촘스키 정규형을 정의하는 또 다른 방법은^[4]^{: 92}^[10] 다음과 같습니다.

형식문법은 Chomsky 축소 형식이며, 모든 생성 규칙이 다음과 같은 형식일 경우에 사용됩니다.

A\rightarrow \,BC

A\rightarrow \,BC

A\rightarrow \,BC

A\rightarrow \,BC

또는

A\rightarrow \,a

A\rightarrow \,a

{\displaystyle A\rightarrow \,a

여기서 $A$ ${\displaystyle A$ $B$ $B$ $및$ C $B$ $C$ 은 $C$ (는) 터미널이 아닌 기호이고 $a$ 은(는) 터미널 기호입니다 $a$ .이 정의를 사용할 경우 $B$ $B$ 또는 $B$ $C$ $C$ 이(가) 시작 기호가 될 수 있습니다 $C$ .빈 문자열을 생성하지 않는 문맥이 없는 문법만이 Chomsky 축소 형식으로 변환될 수 있습니다.

플로이드 정상 형태

BNF(Backus-Naur form)라는 용어를 제안한 편지에서, 도널드 E. 크누스(Donald E. Knuth)는 BNF의 "모든 정의가 그러한 형태를 갖는 구문은 '플로이드 정상 형태'라고 말할 수 있다"고 암시했습니다.

\langle A\rangle ::=\,\langle B\rangle \mid \langle C\rangle

\langle A\rangle ::=\,\langle B\rangle \mid \langle C\rangle

\langle A\rangle ::=\,\langle B\rangle \mid \langle C\rangle

:

=

\langle A\rangle ::=\,\langle B\rangle \mid \langle C\rangle

∣

\langle A\rangle ::=\,\langle B\rangle \mid \langle C\rangle

\langle A\rangle ::=\,\langle B\rangle \mid \langle C\rangle

⟩

{\displaysty

::

langle B\rangle \m

langle

C\rangle }

또는

\langle A\rangle ::=\,\langle B\rangle \langle C\rangle

\langle A\rangle ::=\,\langle B\rangle \langle C\rangle

\langle A\rangle ::=\,\langle B\rangle \langle C\rangle

:

=

\langle A\rangle ::=\,\langle B\rangle \langle C\rangle

⟩

\langle A\rangle ::=\,\langle B\rangle \langle C\rangle

\langle A\rangle ::=\,\langle B\rangle \langle C\rangle

⟩

{\displaysty

::

langle B\rang

langle

C\rangle }

또는

\langle A\rangle ::=\,a

::

{\displaysty

::=\,

a},

여기서 ⟨ $\langle A\rangle$ 는 ${\displaystyle \langle A\rangle$ }을 $\langle A\rangle$ ⟩하고, ⟨ $\langle B\rangle$ 는 ${\displaystyle \langle B\rangle$ } 및 ⟩ $\langle C\rangle$ ⟨ {\ $displaystyle \langle C\rangle}$ 은(는) 터미널 기호이며, $a$ 은(는) 터미널 기호입니다. 플로이드는 1961년에 BNF 구문을 위 구문으로 변환할 수 있다는 것을 발견했습니다.^[11]그러나 그는 "의심할 여지 없이 많은 사람들이 독립적으로 이 단순한 사실을 자신의 작업에 사용해 왔고, 이 점은 플로이드의 노트의 주요 고려 사항에 부수적인 것일 뿐입니다."^[12]라고 이 용어를 철회했습니다.플로이드의 노트가 촘스키의 1959년 기사를 인용한 반면, 크누스의 편지는 그렇지 않습니다.

어플

CNF 변환은 이론적 중요성 외에도 일부 알고리듬에서 사전 처리 단계로 사용됩니다. 예를 들어, CYK 알고리듬, 컨텍스트 없는 문법에 대한 상향식 구문 분석 및 변형 확률론적 CKY.^[13]

참고 항목

백투스-나우르 형태
CYK 알고리즘
Greibach 정상 형태
쿠로다 정상형
문맥이 없는 언어를 위한 펌핑 보조어 - 이의 증명은 Chomsky 정규 형태에 의존합니다.

메모들

^ 즉, 같은 언어를 만들어 내는 사람.
^ 예를 들어, Hopcroft, Ullman(1979)은 TERM과 BIN을 단일 변환으로 병합했습니다.
^ N과 N에 의해 유지 및 생략된 비말단 N을 각각 나타냄
^ 문법에 규칙 S → ε가 있으면 "호출 사이트"가 없으므로 "인라인"할 수 없습니다.따라서 다음 단계에서는 삭제할 수 없습니다.
^ 기호로 측정한 필기 길이

참고문헌

^ Chomsky, Noam (1959). "On Certain Formal Properties of Grammars". Information and Control. 2 (2): 137–167. doi:10.1016/S0019-9958(59)90362-6. 여기: 섹션 6, 페이지 152ff.
^ D'Antoni, Loris. "Page 7, Lecture 9: Bottom-up Parsing Algorithms" (PDF). CS536-S21 Intro to Programming Languages and Compilers. University of Wisconsin-Madison. Archived (PDF) from the original on 2021-07-19.
^ Sipser, Michael (2006). Introduction to the theory of computation (2nd ed.). Boston: Thomson Course Technology. Definition 2.8. ISBN 0-534-95097-3. OCLC 58544333.
^ ^a ^b ^c ^d ^e ^f Hopcroft, John E.; Ullman, Jeffrey D. (1979). Introduction to Automata Theory, Languages and Computation. Reading, Massachusetts: Addison-Wesley Publishing. ISBN 978-0-201-02988-8.
^ Hopcroft, John E.; Motwani, Rajeev; Ullman, Jeffrey D. (2006). Introduction to Automata Theory, Languages, and Computation (3rd ed.). Addison-Wesley. ISBN 978-0-321-45536-9. 섹션 7.1.5, 페이지 272
^ Rich, Elaine (2007). "11.8 Normal Forms". Automata, Computability, and Complexity: Theory and Applications (PDF) (1st ed.). Prentice-Hall. p. 169. ISBN 978-0132288064. Archived from the original (PDF) on 2023-01-17.
^ Wegener, Ingo (1993). Theoretische Informatik - Eine algorithmenorientierte Einführung. Leitfäden und Mongraphien der Informatik (in German). Stuttgart: B. G. Teubner. ISBN 978-3-519-02123-0. 섹션 6.2 "Die Chomsky-Normal form für kontextfreie grammatiken", 페이지 149-152
^ ^a ^b ^c Lange, Martin; Leiß, Hans (2009). "To CNF or not to CNF? An Efficient Yet Presentable Version of the CYK Algorithm" (PDF). Informatica Didactica. 8. Archived (PDF) from the original on 2011-07-19.
^ Allison, Charles D. (2022). Foundations of Computing: An Accessible Introduction to Automata and Formal Languages. Fresh Sources, Inc. p. 176. ISBN 9780578944173.
^ Hopcroft.(2006)^{[page needed]}
^ Floyd, Robert W. (1961). "Note on mathematical induction in phrase structure grammars" (PDF). Information and Control. 4 (4): 353–358. doi:10.1016/S0019-9958(61)80052-1. Archived (PDF) from the original on 2021-03-05. 여기: p.354
^ Knuth, Donald E. (December 1964). "Backus Normal Form vs. Backus Naur Form". Communications of the ACM. 7 (12): 735–736. doi:10.1145/355588.365140. S2CID 47537431.
^ Jurafsky, Daniel; Martin, James H. (2008). Speech and Language Processing (2nd ed.). Pearson Prentice Hall. p. 465. ISBN 978-0-13-187321-6.

추가열람

콜, 리처드.CFG를 CNF(Chomsky Normal Form)로 변환, 2007년 10월 17일 (pdf) — TERM, BIN, START, DEL, UNIT 순서를 사용합니다.
John Martin (2003). Introduction to Languages and the Theory of Computation. McGraw Hill. ISBN 978-0-07-232200-2. (섹션 6.6의 237-240 페이지: 단순화된 양식과 일반적인 양식)
Michael Sipser (1997). Introduction to the Theory of Computation. PWS Publishing. ISBN 978-0-534-94728-6. (섹션 2.1의 98-101페이지: 문맥이 없는 문법.156페이지.)
Charles D. Allison (2021) (20 August 2021). Foundations of Computing: An Accessible Introduction to Formal Language. Fresh Sources, Inc. ISBN 9780578944173. (섹션 7.1 171-183쪽: Chomsky Normal Form)
사이퍼, 마이클계산론 개론, 제2판
Alexander Meduna (6 December 2012). Automata and Languages: Theory and Applications. Springer Science & Business Media. ISBN 978-1-4471-0501-5.

[5] 즉, 같은 언어를 만들어 내는 사람.

[10] 예를 들어, Hopcroft, Ullman(1979)은 TERM과 BIN을 단일 변환으로 병합했습니다.

[11] N과 N에 의해 유지 및 생략된 비말단 N을 각각 나타냄

[12] 문법에 규칙 S → ε가 있으면 "호출 사이트"가 없으므로 "인라인"할 수 없습니다.따라서 다음 단계에서는 삭제할 수 없습니다.

[14] 기호로 측정한 필기 길이

[1] Chomsky, Noam (1959). "On Certain Formal Properties of Grammars". Information and Control. 2 (2): 137–167. doi:10.1016/S0019-9958(59)90362-6. 여기: 섹션 6, 페이지 152ff.

[2] D'Antoni, Loris. "Page 7, Lecture 9: Bottom-up Parsing Algorithms" (PDF). CS536-S21 Intro to Programming Languages and Compilers. University of Wisconsin-Madison. Archived (PDF) from the original on 2021-07-19.

[3] Sipser, Michael (2006). Introduction to the theory of computation (2nd ed.). Boston: Thomson Course Technology. Definition 2.8. ISBN 0-534-95097-3. OCLC 58544333.

[Hopcroft.Ullman.1979-4] ^ ^a ^b ^c ^d ^e ^f Hopcroft, John E.; Ullman, Jeffrey D. (1979). Introduction to Automata Theory, Languages and Computation. Reading, Massachusetts: Addison-Wesley Publishing. ISBN 978-0-201-02988-8.

[6] Hopcroft, John E.; Motwani, Rajeev; Ullman, Jeffrey D. (2006). Introduction to Automata Theory, Languages, and Computation (3rd ed.). Addison-Wesley. ISBN 978-0-321-45536-9. 섹션 7.1.5, 페이지 272

[7] Rich, Elaine (2007). "11.8 Normal Forms". Automata, Computability, and Complexity: Theory and Applications (PDF) (1st ed.). Prentice-Hall. p. 169. ISBN 978-0132288064. Archived from the original (PDF) on 2023-01-17.

[8] Wegener, Ingo (1993). Theoretische Informatik - Eine algorithmenorientierte Einführung. Leitfäden und Mongraphien der Informatik (in German). Stuttgart: B. G. Teubner. ISBN 978-3-519-02123-0. 섹션 6.2 "Die Chomsky-Normal form für kontextfreie grammatiken", 페이지 149-152

[Lange.Leis.2009-9] Lange, Martin; Leiß, Hans (2009). "To CNF or not to CNF? An Efficient Yet Presentable Version of the CYK Algorithm" (PDF). Informatica Didactica. 8. Archived (PDF) from the original on 2011-07-19.

[13] Allison, Charles D. (2022). Foundations of Computing: An Accessible Introduction to Automata and Formal Languages. Fresh Sources, Inc. p. 176. ISBN 9780578944173.

[15] Hopcroft.(2006)^{[page needed]}

[16] Floyd, Robert W. (1961). "Note on mathematical induction in phrase structure grammars" (PDF). Information and Control. 4 (4): 353–358. doi:10.1016/S0019-9958(61)80052-1. Archived (PDF) from the original on 2021-03-05. 여기: p.354

[knuth1964-17] Knuth, Donald E. (December 1964). "Backus Normal Form vs. Backus Naur Form". Communications of the ACM. 7 (12): 735–736. doi:10.1145/355588.365140. S2CID 47537431.

[18] Jurafsky, Daniel; Martin, James H. (2008). Speech and Language Processing (2nd ed.). Pearson Prentice Hall. p. 465. ISBN 978-0-13-187321-6.

[1]

[2]

[3]

[note 1]

[4]

[5]

[6]

[7]

[note 3]

[9]

[note 5]

[8]

[10]

[11]

[12]

[13]

Search

촘스키 정상형

네임스페이스

더

목차

문법을 Chomsky 정규 형태로 변환

시작: 오른쪽에서 시작 기호를 제거합니다.

용어: 단독 터미널이 없는 규칙 제거

BIN: 2개 이상의 단자가 있는 우측면 제거

DEL: ε 규칙 제거

유닛: 유닛 규칙 제거

변환순서

예

대체정의

촘스키 축소형

플로이드 정상 형태

어플

참고 항목

메모들

참고문헌

추가열람