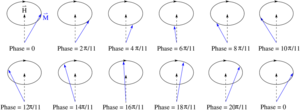
스핀파

이 글은 일반적인 참고문헌 목록을 포함하고 있지만, 그에 상응하는 인라인 인용구가 충분하지 않기 때문에 대체로 검증되지 않은 상태로 남아 있다. 보다 정확한 인용구를 도입하여 이 기사를 개선할 수 있도록 도와주십시오. (2013년 12월) (이 템플릿 메시지를 제거하는 방법 및 시기 알아보기)

스핀파(spin wave)는 자성 물질의 순서에 있어서 전파 교란이다. 이러한 저지대 집단적 흥분은 연속적인 대칭성을 가진 자기 격자에서 발생한다. 등가 퀘이시입자의 관점에서 보면 스핀파는 마그놀로지로 알려져 있는데, 이는 핵 격자의 음소 배설물에 대략 대응하는 스핀 격자의 보소닉 모드다. 온도가 증가함에 따라 스핀파의 열적 흥분은 강자석의 자발적 자성을 감소시킨다. 스핀파의 에너지는 상온 이하에서 전형적인 퀴리 지점과 일치하는 μeV에 불과하다.

이론

스핀파를 이해하는 가장 간단한 방법은 하이젠베르크 $페로마그네틱$에 대해$$ 해밀턴 H ${\${\$mathcal{H}}$를 고려하는 것이다.

${\displaystyle {\mathcal {H}}=-{\frac {1}{2}}J\sum _{i,j}\mathbf {S} _{i}\cdot \mathbf {S} _{j}-g\mu _{\rm {B}}\sum _{i}\mathbf {H} \cdot \mathbf {S} _{i}}$

여기서 J는 교환 에너지, 연산자 S는 브라바이스 격자점에서 스핀을 나타내고, g는 란데 g-요인, μ는_B 보어 마그네톤, H는 외부 장과 "분자" 장을 포함하는 내부 장이다. 고전적 연속체 사례와 1 + 1 차원에서는 하이젠베르크 페로마그넷 방정식의 형태가 있다는 점에 유의하십시오.

${\displaystyle \mathbf {S} _{t}=\mathbf {S} \time \mathbf {S} _{xx}.}$

1 + 1, 2 + 1 및 3 + 1 차원에서는 이 방정식이 란도-라이프시츠 방정식, 이시모리 방정식 등과 같은 몇 가지 통합 및 비통합 확장을 허용한다. 페롬자석 J > 0과 해밀턴 ${\displaystyle 0\mathrm{}}$ ⟩${\displaystyle 0\rangele}$의 접지 상태는 모든 스핀이 필드 H와 평행하게 정렬되는 것이다$$. $⟩{\displaystyle 0\rangele}$은(는) $H{\displaystyle \mathcal{}}$ ${\$의 고유 상태를 다음과 같은 방법으로 스핀 상승 및 스핀 하강 연산자의 관점에서 다시 작성하면 확인할$$ 수 있다.

${\displaystyle S^{\pm }=S^{x}\pm iS^{y}}}$

결과적으로

${\displaystyle {\mathcal{H}=-{\frac {1}{2}}J\sum _{i,j}S_{i}^{z}S_{j}^{z}-g\mu _{\rm{B}}H\sum _{i}S_{i}^{z}-{\frac {1}{4}J\sum _{i,j}(S_{i}^{+}S_{j}^{-}}}S_{i}^{-}S_{j}^{j}^{-}}}}}}}}}$

여기서 z는 자기장의 방향으로 선택되었다. 스핀 로어링 연산자 S는⁻ z축을 따라 스핀의 최소 투영으로 상태를 소멸시키고, 스핀 상승 연산자 S는⁺ z축을 따라 최대 스핀 투영으로 지상 상태를 소멸시킨다. 이후

${\displaystyle S_{i}^{z} 0\rangele =s 0\rangele }$

최대 정렬 상태의 경우

${\displaystyle {\mathcal {H} 0\rangele =\왼쪽(-Js^{2}-g\mu_{\rm{B}Hs\right)N 0\rangele }$

여기서 N은 브라바이스 격자 사이트의 총 수입니다. 지상국이 해밀턴주의 고유국가라는 명제는 확인된다.

해밀턴의 첫 흥분 상태가 내가 회전한 위치에서 무작위로 선택한 스핀을 하나 가지고 있다고 추측할 수 있다.

${\displaystyle S_{i}^{z} 1\rangele =(s-1) 1\rangele ,}$

그러나 사실 이러한 스핀들의 배열은 고유 국가가 아니다. 그 이유는 그러한 상태가 스핀 상승 및 하강 사업자에 의해 변화되기 때문이다. 연산자 ${\displaystyle {Si}_{}^{}}$+ ${\$는 위치 i에서 스핀의 z-투여를 저에너지 방향으로 다시 증가시키지만$$, $연산자{\displaystyle {}_{}^{}}$ S ${\displaystyle j_{}^{}}$ -${\$는 위치 j에서 스핀의 z투여를 낮춘다$$. 따라서 두 연산자의 결합 효과는 회전된 스핀을 새로운 위치로 전파하는 것인데, 이는 올바른 고유 상태가 스핀파, 즉 스핀이 한 번 줄어든 상태의 중첩이라는 암시다. 한 스핀의 방향 변경과 관련된 교환 에너지 벌칙은 교란을 긴 파장으로 확산시킴으로써 감소한다. 따라서 가까운 두 개의 스핀의 방향 오차는 최소화된다. 이 설명에서, 분리된 대칭을 가진 Ising 모델 자석에는 스핀파가 없는 이유를 알 수 있다: 스핀 격자의 교란을 긴 파장에 걸쳐 확산시킨다는 개념은 스핀들이 두 가지 방향만 가지고 있을 때 말이 되지 않는다. 저에너지 배설물의 존재는 외부 장이 없을 때 스핀 시스템이 무한히 많은 변질된 지반 상태를 가지고 있고 무한히 다른 스핀 방향을 가지고 있다는 사실과 관련이 있다. 이러한 지상 상태의 존재는 상태 ${\displaystyle 0\mathrm{}}$⟩ ${\displaystyle 0\rangele}$이(가) 해밀턴 $H{\displaystyle \mathcal{}}$ ${\$ {$H}$의 완전한 회전 대칭을 가지고 있지$$ 않다는 사실에서 알 수 있는데$,$ 이것은 자발적 대칭 파괴라고 하는 현상이다.

자기화

이 모델에서 자기화

${\displaystyle M={\frac {N\mu_{\rm{B}gs}{{\displaystyle M={\frac {N\m브이}}$

여기서 V는 볼륨이다. 스핀파의 전파는 란다우-라이프시츠 운동 방정식으로 설명된다.

${\d\mathbf{M}}{dt}=-\gamma \mathbf {M} \times \mathbf {H}-{\frac {\lambda \mathbf {M} \times \mathbf {H}{M}}}}{M^2}}: \}$

여기서 γ은 자성비, λ은 감쇠 상수. 이 금지되어 보이는 방정식의 교차 생산물은 스핀파의 전파가 내부와 외부장에서 발생하는 토크의 지배를 받는다는 것을 보여준다. (등가 형태는 란도-라이프시츠-길버트 방정식으로 최종 용어를 보다 "간단하게 보이는" 등가물로 대체한다.)

방정식의 오른쪽에 있는 첫 번째 항은 적용된 장의 영향을 받는 자성의 전 과정을 기술하고, 위에서 언급한 최종 항은 시간이 경과함에 따라 자기장 방향을 향해 자화 벡터가 "영"하는 방법을 설명한다. 금속에서 상수 λ에 의해 설명되는 감쇠력은 많은 경우에 와류로 지배된다.

음운과 마그너의 중요한 차이점은 그들의 분산 관계에 있다. 음핵의 분산관계는 우선 파동 벡터 k에서 선형, 즉 ω = ck, 여기서 Ω은 주파수, 마그논은 포물선 분산 관계를 가지고 있다: ώ = Ak² 매개변수 A가 "spin 뻣뻣함"을 나타낸다. k² 형식은 S_i ⋅ S_j 도트 제품에서 유래한 에너지 표현에서 코사인 용어의 테일러 팽창의 세 번째 용어다. 분산관계의 차이에 대한 근본적인 이유는 페로마네트의 지상상태에 대한 순서 매개변수(자기화)가 시간역대칭성을 위반하기 때문이다. 격자 상수 a를 가진 고체에서 인접한 두 개의 회전은 파동 벡터 k를 가진 모드에 참가하며 그 사이에 ka와 동일한 각도를 가진다.

실험관찰

스핀파는 비탄성 중성자 산란, 비탄성 광 산란(Brillouin 산란, 라만 산란 및 비탄성 X선 산란), 비탄성 전자 산란(spin-revolvolved electrons energy loss spectroscopy), 스핀파 공명(발광공명)의 네 가지 실험 방법을 통해 관측된다. 첫 번째 방법에서는 일반적으로 산란 벡터(또는 동등하게 운동량 전달), 온도 및 외부 자기장의 함수로써 마그논을 흥분시키는 중성자 빔의 에너지 손실을 측정한다. 비탄성 중성자 산란 측정은 음운과 마찬가지로 마그노에 대한 분산 곡선을 결정할 수 있다. 중요한 비탄성 중성자 산란 설비는 영국 옥스퍼드셔의 IS 중성자 소스, 프랑스 그르노블의 라우에-란제빈 연구소, 미국 테네시 오크리지 국립연구소의 고융제 동위원소 원자로, 미국 메릴랜드의 국립표준기술연구소에도 있다.브릴루우 나도 마찬가지로 산란한다.자성 물질에서 반사되거나 자성 물질로 전달되는 광자(보통 편리한 가시 파장)의 에너지 손실을 돕는다. 브릴루인 분광법은 더 널리 알려진 라만 산란과 유사하지만, 더 낮은 에너지를 탐사하고 마그노의 meV 에너지를 검출할 수 있도록 에너지 분해능이 우수하다. 대신 강자성(또는 반자성) 공명은 일반적으로 각도, 온도 및 도포장의 함수로서 자성 물질에 의한 전자파의 흡수, 자성 물질에서의 입사 등을 측정한다. 강자성 공명은 자석크리스탈린 음이소트로피가 스핀파 분산에 미치는 영향을 판단하는 편리한 실험실 방법이다. 독일 할레의 맥스 플랑크 미세구조물리학 연구소의 한 그룹은 스핀 편광 전자 에너지 손실 분광기(SPEELS)를 사용함으로써 매우 높은 에너지 표면 마그노들이 흥분할 수 있다는 것을 증명했다. 이 기술은 울트라틴 강자성 필름에서 마그노의 분산을 조사할 수 있게 해준다. 첫 번째 실험은 5 ML Fe 필름에 대해 수행되었다.^[1] 모멘텀 분해능을 통해, 각각 Cu(001)의 8 ML FCC Co 필름과 W(110)의 8 ML hcp Co 필름에 대해 마그논 분산을 탐구했다.^[2] 표면 브릴루인 구역의 경계에 있는 최대 마그논 에너지는 240 mV였다.

실제적 유의성

자기 전자 소자가 고주파에서 작동될 때 스핀파의 발생은 중요한 에너지 손실 메커니즘이 될 수 있다. 스핀파 생성은 선폭을 제한하고 따라서 마이크로파 장치에 사용되는 페라이트 구성 요소의 품질 계수 Q를 제한한다. 자성 물질의 특성 스핀파의 가장 낮은 주파수의 역수는 그 물질에 기초한 장치의 전환에 대한 시간 척도를 제공한다.

참고 항목

• 매그노닉스
• 홀슈타인-프리마코프 변환
• 스핀 엔지니어링

참조

외부 링크

• 스핀 웨이브 비엔날레 국제 심포지엄은 자성을 주문하는 다양한 재료의 동적 특성에 대한 기초 연구의 최신 진보를 논의하기 위한 것이다.
• 브릴루인 산란 측정을 수행하는 실험실 목록