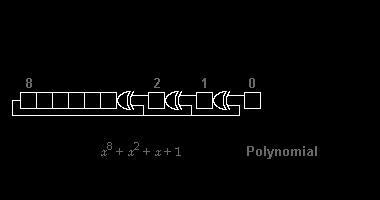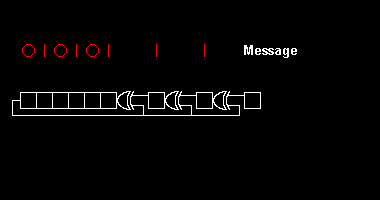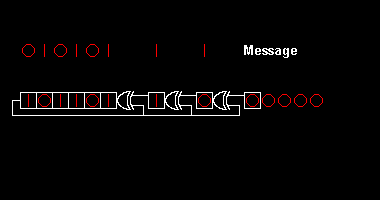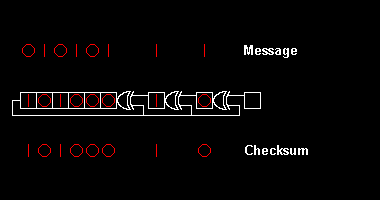순환 중복 검사 계산

주기적 중복 검사 계산은 다항분할 모듈로 2의 수학에서 도출된다.실제로, 이것은 배타적 또는 연산이 감산을 대체한다는 점을 제외하고 "제너레이터 다항식" 문자열로 고정된 수의 0이 추가된 이진 메시지 문자열의 긴 분할과 유사하다.이러한 유형의 분할은 수정된 시프트 레지스터에 의해 하드웨어 ^[1]및 일련의 동등한 알고리즘에 의해 효율적으로 실현되며, 수학에 가까운 단순한 코드에서 시작하여 바이트와 병렬 처리 및 공간-시간 트레이드오프를 통해 더 빨라지고(그리고 거의 틀림없이 더 난독화됨^[2])된다.

8비트 CRC 생성 예제.발전기는 발전기 다항식 X의 출력(흰색 번호)에 따라 배치된 XOR 게이트를 가진 갈루아식 시프트 레지스터다.메시지 스트림은 어떤 길이든 될 수 있다.레지스터를 통해 이동된 후 8개의 0이 지나면 레지스터의 결과는 체크섬이다.

체크섬을 사용하여 수신된 데이터 확인수신된 메시지는 발전기에서 사용하는 것과 동일한 레지스터를 통해 이동되지만 수신된 체크섬은 0이 아닌 0이 붙어 있다.정확한 데이터는 0으로 결과를 산출한다; 메시지나 체크섬의 손상된 비트는 다른 결과를 주며, 오류가 발생했음을 경고한다.

다양한 CRC 표준은 초기 시프트 레지스터 값, 최종 배타적-Or 단계 및 가장 중요한 비트 순서(엔디안티)를 지정하여 다항 분할 알고리즘을 확장한다.그 결과 실제로 보이는 코드는 "순수" 구분에서 혼동할 정도로 벗어나며,^[2] 기록부는 좌우로 이동할 수 있다.

예

하드웨어에서 다항식 분할을 구현하는 예로서, ASCII 문자 "W"로 만들어진 8비트 메시지의 8비트 CRC(이진수 01010111₂, 10진수 87₁₀ 또는 16진수 57₁₆)를 계산하려고 한다고 가정해 보십시오.그림의 경우 CRC-8-ATM(HEC) $x^{8}+x^{2}+x+1$ $x^{8}+x^{2}+x+1$ 8 $x^{8}+x^{2}+x+1$ + $x^{8}+x^{2}+x+1$ 2 $x^{8}+x^{2}+x+1$ + x $x^{8}+x^{2}+x+1$ + 1 ${\displaystyle x^{8}+x^{2}+x+1$ } $x^{8}+x^{2}+x+1$ .왼쪽에서 전송된 첫 번째 비트( $x$ $x$ 의 최고 출력의 계수 $x$ 를 작성하면, 이는 9비트 문자열 "100000111"에 해당한다.

바이트 값 57은₁₆ 사용된 비트 순서 규칙에 따라 두 개의 다른 순서로 전송할 수 있다.Each one generates a different message polynomial $M(x)$ . Msbit-first, this is $x^{6}+x^{4}+x^{2}+x+1$ = 01010111, while lsbit-first, it is $x^{7}+x^{6}+x^{5}+x^{3}+x$ = 11101010.그런 다음 x $x^{8}$ ${\$ 을 곱하여 $x^{8}$ 두 개의 16비트 메시지 다항식 x $x^{8}M(x)$ M $x^{8}M(x)$ ( $){\displaystyle x^{8}M(x)}$ 을(를) 생성할 수 있다 $x^{8}M(x)$

나머지를 계산하는 것은 발전기 다항식 $G(x)$ $G(x)$ $G(x)$ $G(x)$ 의 배수량을 빼는 것으로 구성된다 $G(x)$ 이것은 십진수 긴 분할과 같으나, 각 단계에서 가능한 유일한 배수량은 0과 1이고, 소급은 위쪽 자릿수를 줄이는 대신 "무한도"에서 차용하기 때문에 더욱 간단하다.우리는 시세를 신경 쓰지 않기 때문에 그것을 기록할 필요가 없다.

가장 중요한 비트 우선

최하위 비트 먼저

	0	1	0	1	0	1	1	1	0	0	0	0	0	0	0	0
−	0	0	0	0	0	0	0	0	0
=	0	1	0	1	0	1	1	1	0	0	0	0	0	0	0	0
	−	1	0	0	0	0	0	1	1	1
=	0	0	0	1	0	1	1	0	1	1	0	0	0	0	0	0
		−	0	0	0	0	0	0	0	0	0
=	0	0	0	1	0	1	1	0	1	1	0	0	0	0	0	0
			−	1	0	0	0	0	0	1	1	1
=	0	0	0	0	0	1	1	0	1	0	1	1	0	0	0	0
				−	0	0	0	0	0	0	0	0	0
=	0	0	0	0	0	1	1	0	1	0	1	1	0	0	0	0
					−	1	0	0	0	0	0	1	1	1
=	0	0	0	0	0	0	1	0	1	0	1	0	1	1	0	0
						−	1	0	0	0	0	0	1	1	1
=	0	0	0	0	0	0	0	0	1	0	1	0	0	0	1	0
							−	0	0	0	0	0	0	0	0	0
=	0	0	0	0	0	0	0	0	1	0	1	0	0	0	1	0

	1	1	1	0	1	0	1	0	0	0	0	0	0	0	0	0
−	1	0	0	0	0	0	1	1	1
=	0	1	1	0	1	0	0	1	1	0	0	0	0	0	0	0
	−	1	0	0	0	0	0	1	1	1
=	0	0	1	0	1	0	0	0	0	1	0	0	0	0	0	0
		−	1	0	0	0	0	0	1	1	1
=	0	0	0	0	1	0	0	0	1	0	1	0	0	0	0	0
			−	0	0	0	0	0	0	0	0	0
=	0	0	0	0	1	0	0	0	1	0	1	0	0	0	0	0
				−	1	0	0	0	0	0	1	1	1
=	0	0	0	0	0	0	0	0	1	0	0	1	1	0	0	0
					−	0	0	0	0	0	0	0	0	0
=	0	0	0	0	0	0	0	0	1	0	0	1	1	0	0	0
						−	0	0	0	0	0	0	0	0	0
=	0	0	0	0	0	0	0	0	1	0	0	1	1	0	0	0
							−	0	0	0	0	0	0	0	0	0
=	0	0	0	0	0	0	0	0	1	0	0	1	1	0	0	0

각 뺄셈 후에 비트는 세 개의 그룹으로 나뉜다: 처음부터 모두 0인 그룹, 마지막에는 원본에서 변하지 않는 그룹, 그리고 중간에는 "흥미로운" 파란색 음영 그룹으로 나뉜다."흥미있는" 그룹의 길이는 8비트이며, 다항식의 정도와 일치한다.단계마다 다항식의 적절한 배수를 빼서 0그룹을 한 번 더 길게 만들고, 변하지 않은 그룹은 마지막 남은 부분만 남을 때까지 한 번 더 짧아진다.

msbit-first 예제에서 나머지 다항식은 x $x^{7}+x^{5}+x$ + $x^{7}+x^{5}+x$ $x^{7}+x^{5}+x$ + x ${\displaystyle$ x $^{7}+x^{5}+x}$ 입니다 $x^{7}+x^{5}+x$ x의 가장 높은 검정력이 msbit, 이것이 A2라는₁₆ 관례를 사용하여 16진수로 변환한다.lsbit-first에서 나머지는 $x^{7}+x^{4}+x^{3}$ $x^{7}+x^{4}+x^{3}$ + x $x^{7}+x^{4}+x^{3}$ + x $x^{7}+x^{4}+x^{3}$ ${\$ x $^{7}+x^{4}+x^{3$ x의 최고 전력이 lsbit이라는 관례를 사용하여 16진법으로 변환하면, 이것은 19이다₁₆.

실행

위의 예에서처럼 각 단계에서 전체 메시지를 작성하는 것은 매우 지루하다.효율적인 구현에서는 $n$ $n$ -bit $n$ 시프트 레지스터를 사용하여 흥미로운 비트만 보관한다.다항식을 $x$ $x$ 에 곱하는 것은 $x$ 계수가 값이 변하지 않고 다항식의 다음 기간까지만 이동하기 때문에 레지스터를 한 자리 이동시키는 것과 같다.

여기 n-bit CRC 계산을 위한 일부 유사 코드의 초안이 있다.다항식(다항식)에 대해 계산된 복합 데이터 유형을 사용한다.x 정수 변수가 아니라 추가, 증분 및 지수화할 수 있는 다항식 객체를 생성하는 생성자다.에게xor두 개의 다항식(modulo 2)을 추가하는 것이다. 즉, 두 다항식으로부터 각 일치 항의 계수를 배타적으로 OR한다.

함수 crc(비트 어레이 bitString[1..)렌],int에 살고 있는데){remainderPolynomial:인기 다양한 보완책 remainderPolynomial 여기 //은 메시지의 첫번째 n비트//= polynomialForm(bitString[1..n]), 아래 나는 1len까지 −1에 제맵핑 하는 보{:=remainderPolynomial*x+remainderPolynomial bitString[i+n]*x0, len k&gt에 bitString[k]=0 정의 // 만약 xn의 계수.r의emainderPolynomial = 1 { remariPolynomial := remariousPolynomial xor generatorPolynomial } } // 여기서 인기 있는 변형이 나머지 Polynomial을 보완함; 아래의 § post-invertive를 참조하십시오.

코드 조각 1: 단순 다항식 분할

이 예제 코드는 바이트를 사용하지 않음으로써 비트 순서 규칙을 지정할 필요가 없다는 점에 유의하십시오.bitString이미 비트 배열의 형태로 되어 있고remainderPolynomial다항식 연산의 관점에서 조작된다. $x$ $x$ 에 의한 곱셈은 왼쪽 또는 오른쪽 교대조일 수 있고 $x$ ,bitString[i+n]레지스터의 오른쪽 끝 또는 왼쪽 끝일 수 있는 $x^{0}$ $x^{0}$ ${\$ x $^{0}$ 계수로 $x^{0}$ 한다.

이 코드는 두 가지 단점이 있다.첫째, 실제로 n+1비트 레지스터를 사용하여remainderPolynomial $x^{n}$ $x^{n}$ ${\$ 계수를 $x^{n}$ 테스트할 수 있도록 한다.더 중요한 것은, 그것은bitString0 비트로 패드를 채우는 것.

첫 번째 문제는 x $x^{n-1}$ - 1 ${\$ 계수 테스트를 $x^{n-1}$ 통해 해결할 수 있다.remainderPolynomial $x$ $x$ 을(를) 곱하기 전에 $x$

두 번째 문제는 마지막 n번 반복을 다르게 함으로써 해결할 수 있지만 하드웨어와 소프트웨어 구현 모두에서 보편적으로 사용되는 보다 미묘한 최적화가 있다.

메시지에서 발전기 다항식을 빼는 데 사용되는 XOR 연산은 역순이고 연관성이 있기 때문에, 다양한 입력이 어떤 순서로 결합되든 상관없다.remainderPolynomial. 그리고 구체적으로는, 어느 정도.bitString에 추가할 필요가 없음remainderPolynomial할 것인지 아닌지를 판단하기 위해 시험하는 마지막 순간까지.xor…과 함께generatorPolynomial.

이렇게 하면 사전 로딩이 필요 없음remainderPolynomial메시지의 첫 번째 n개 비트와 함께:

함수 crc(비트 어레이 bitString[1..)렌],int에 살고 있는데){remainderPolynomial:= 0지금 인기 있는 변형 보완 remainderPolynomial //, 제맵핑 하는 아래 나는 1len에{:=1{remainderPolynomial:=(remainderPolynomial의 xn−1의 계수)(remainderPolynomial=remainderPolynomialxor(bitstring[나는]때에요 xn−1)remainderPolynomial에서 −1을 보여 줍니다.*x)xor generatorPolynomial } 다른 { 나머지 Polynomial := (remainDolynomial * x) } } // 여기서 인기 있는 변형이 나머지 Polynomial을 보완함; 아래의 § 포스트인버스트 나머지 Polynomial }을 참조하십시오.

코드 조각 2: 메시지 XORing이 지연된 다항식 분할

이것은 표준 비트-타임 하드웨어 CRC 구현이며 연구할 가치가 충분히 있다. 왜 이것이 첫 번째 버전과 정확히 동일한 결과를 계산하는지 이해하면 나머지 최적화는 매우 간단하다.만약remainderPolynomial길이가 n비트인 다음, 그것과 그것의 계수 $x^{n}$ $x^{n}$ $x^{n}$ {\ $displaystyle$ x^{ $n}}$ generatorPolynomial그냥 버려진다.이는 일반적으로 선행 계수가 생략된 상태에서 CRC 다항식이 2진수로 작성되는 것을 볼 수 있는 이유다.

소프트웨어에서, 사람들은 시간을 늦출 수 있지만, 주목하는 것은 편리하다.xor마지막 순간까지 각각의 비트를 더 일찍 하는 것도 가능하다.보통 공연하는 것이 편리하다.xor한 번에 바이트 수, 심지어 이와 같은 비트-타임 구현 시에도:

함수 crc(바이트 배열 문자열[1..])len], int len) {     remainderPolynomial := 0     // A popular variant complements remainderPolynomial here; see § Preset to −1 below for i from 1 to len {         remainderPolynomial := remainderPolynomial xor polynomialForm(string[i]) * xⁿ⁻⁸ for j from 1 to 8 {    // Assuming 8 bits per byte if coefficient of xⁿ⁻¹ of remainderPolynomial = 1 {나머지 폴리노멀 :=(remainDolynomial * x) xor 생성기폴리노멀 } 기타 { 나머지 폴리노멀 :=(remainDolynomial * x) } } // 여기서 나머지 폴리노멀을 보완하는 인기 있는 변종. § 아래의 나머지 폴리노멀리즘 }을 참조하십시오.

코드 조각 3: 바이트 문자 XORing이 있는 다항식 분할

이것은 보통 공간이 속도보다 프리미엄이 높을 때 마이크로컨트롤러에서 사용되는 가장 컴팩트한 소프트웨어 구현이다.

비트 순서(내부성)

비트 직렬 하드웨어에서 구현될 때 제너레이터 다항식은 비트 할당을 고유하게 설명하며, 전송되는 첫 번째 비트는 $항상$ x $x$ 의 최고 출력의 계수이며 $x$ 마지막 $n$ $n$ 비트는 $n$ coef로 시작하는 CRC 나머지 $R(x)$ ) ${\displaystystyle R(x$ 이다. $x^{n-1}$ $x^{n-1}$ - $x^{n-1}$ ${\$ 의 부족이고 $x^{n-1}$ x $x^{0}$ ${\$ a.k.a의 계수로 끝맺는다.

그러나 병렬 전송을 사용할 때, 8B/10B 인코딩 또는 RS-232 형식의 비동기 시리얼 통신을 사용할 때와 같이 비트가 한 번에 바이트를 처리할 때, 또는 소프트웨어에서 CRC를 구현할 때, 데이터의 비트 순서(엔디안티)를 지정할 필요가 있다. 각 바이트의 비트는 "첫 번째"로 간주되며, 다음이 될 것이다. $x$ $x$ 의 높은 검정력 계수 $x$

데이터가 직렬 통신에 사용될 경우, 데이터가 궁극적으로 전송될 비트 순서를 사용하는 것이 가장 좋다.이는 버스트 오류를 감지하는 CRC의 능력은 다항식 $){\displaystyle M(x)}$ 메시지에서 근접성을 기반으로 하기 때문이다 $M(x)$ 인접한 다항식 용어가 순차적으로 전송되지 않을 경우, 비트의 재배열로 인해 한 길이의 물리적 오류 버스트가 더 긴 버스트로 보일 수 있다.

예를 들어 IEEE 802(이더넷) 및 RS-232(시리얼 포트) 표준 모두 최소 중요 비트 우선 전송(리틀 엔디안)을 지정하므로, 이러한 링크를 통해 전송되는 데이터를 보호하기 위한 소프트웨어 CRC 구현은 각 바이트의 최소 중요 비트를 $x$ ${\displaystyle$ x $}$ 의 최고 출력 계수에 매핑해야 한다 $x$ d, 플로피 디스크 및 대부분의 하드 드라이브는 각 바이트의 가장 중요한 비트를 먼저 쓴다.

lsbit-first CRC는 소프트웨어에서 구현하는 것이 약간 더 간단하기 때문에 다소 더 흔히 볼 수 있지만, 많은 프로그래머들은 msbit-first 비트 순서를 따르기가 더 쉽다고 생각한다.따라서 예를 들어 소프트웨어에서 CRC를 초기에 사용한 XMODEM-CRC 확장은 msbit-first CRC를 사용한다.

$x$ 까지 가성소드는 가성소드의 이동을 x $x$ 에 의한 곱으로 기술하고 $x$ 2진에서 다항식으로의 명시적 변환을 작성함으로써 바이트 내 비트의 순서를 지정하는 것을 피했다.실제로 CRC는 특정 비트 순서 규칙을 사용하여 표준 바이너리 레지스터로 유지된다.msbit-first 형식에서는 가장 유의한 이진 비트가 먼저 전송되어 고차 다항식 계수를 포함하고 lsbit-first 형식에서는 최하위 이진 비트가 고차 계수를 포함하고 있다.위의 가성형은 두 가지 형태로 모두 쓸 수 있다.구체성의 경우 16비트 CRC-16-CCITT 다항식 x $x^{16}+x^{12}+x^{5}+1$ + x $x^{16}+x^{12}+x^{5}+1$ + $x^{16}+x^{12}+x^{5}+1$ $x^{16}+x^{12}+x^{5}+1$ + 1 ${\displaystyle x^{16}+x^{12}+x^{5}+$ 1}+ $1$

// 가장 중요한 비트 우선(빅엔디안) // x^16+x^12+x^5+1 = (1) 0001 0000 0010 0001 = 0x1021 함수 crc(바이트 배열 문자열[1].len], int len) {     rem := 0     // A popular variant complements rem here for i from 1 to len {         rem  := rem xor (string[i] leftShift (n-8))   // n = 16 in this example for j from 1 to 8 {   // Assuming 8 bits per byte if rem and 0x8000 {   // if leftmost (most significant) bit is set                 rem  := (rem leftShift 1) xor 0x1021} 다른 {rem :=rem 왼쪽Shift 1 } 렘 := rem 및 0xff // 나머지를 16비트로 트리밍 } } // 여기서 인기 있는 보완 렘 렘 렘 렘 렘 렘 렘}

코드 조각 4: 시프트 레지스터 기반 부서, MSB 우선

// 최하위 비트 먼저(리틀 엔디안) // x^16+x^12+x^5+1 = 1000 0100 0000 1000(1) = 0x8408 함수 crc(바이트 배열 문자열[1].len], int len) { rem := 0 // 여기서 렘 : 1 ~ len { 렘 := 렘 : 1 ~ 8 {/ 바이트당 8비트 및 가장 오른쪽(가장 중요한) 비트가 설정된 경우 := (rem 우측 Shift 1) x 8408 } 기타 {}렘 := rem rightShift 1 } } } } // 여기서 rem 렘을 보완하는 인기 있는 변형 렘 렘 렘}

코드 조각 5: 시프트 레지스터 기반 디비전, LSB 우선

lsbit-first 폼은 이동할 필요가 없다는 점에 유의string[i]전에xor. 두 경우 모두 선택한 비트 순서 지정 규칙과 일치하는 순서로 CRC의 바이트를 전송하십시오.

멀티비트 연산

Sarwate 알고리즘(단일 조회 테이블)

다른 공통 최적화에서는 최고 순서 계수에 의해 인덱싱된 룩업 테이블을 사용한다.rem1회당 2비트 이상의 배당금을 처리한다.^[3]가장 일반적으로 256-엔트리 조회 테이블을 사용하여 내부 루프를 대체한다.j다음 항목 포함:

// Msbit-first rem = (rem 왼쪽 Shift 8) xor big_endian_table[string[i] xor (좌측 렘 왼쪽 8비트) rightShift (n-8) // Lsbit-first rem = (rem 오른쪽 Shift 8) xor lit_endian_table[i] xor (우측 riging] xor (최대 8비트)

코드 조각 6: 테이블 기반 분할 코어

가장 흔히 접하는 CRC 알고리즘 중 하나는 (다른 것 중) 이더넷, FDDI, ZIP 및 기타 아카이브 형식과 PNG 이미지 형식에 의해 사용되는 CRC-32로 알려져 있다.다항식은 msbit-first로 0x04C11로 쓸 수 있다.DB7 또는 0xEDB88320으로 lsbit-first.PNG의 W3C 웹페이지에는 CRC-32의 C에 짧고 간단한 테이블 중심 구현이 포함된 부록이 포함되어 있다.^[4]코드는 여기에 제시된 lsbit-first-at-a-time 유사코드에 해당하며, 테이블은 비트-at-a-time 코드를 사용하여 생성된다는 점에 유의하십시오.

256입력 테이블을 사용하는 것이 보통 가장 편리하지만, 다른 사이즈도 사용할 수 있다.소형 마이크로컨트롤러에서는 16-엔트리 테이블을 사용하여 한 번에 4비트를 처리하면 테이블을 작게 유지하면서 유용한 속도 향상을 얻을 수 있다.저장 공간이 넉넉한 컴퓨터에서는 65536 엔트리 테이블을 사용하여 한 번에 16비트를 처리할 수 있다.

테이블 생성

테이블을 생성하기 위한 소프트웨어는 너무 작고 빨라서 보통 스토리지에서 사전 계산된 테이블을 로드하는 것보다 프로그램 시작 시 계산하는 것이 더 빠르다.한 가지 일반적인 기술은 한 번에 256회 비트 코드를 사용하여 256개의 가능한 8비트 바이트의 CRC를 생성하는 것이다.단, 이는 해당 부동산을 활용해 크게 최적화할 수 있다.table[i xor j] == table[i] xor table[j]. 두 개의 힘에 해당하는 테이블 항목만 직접 계산하면 된다.

다음 예제 코드에서,crc의 가치가 있다table[i]:

big_endian_table[0] := 0 crc := 0x8000 // Assuming a 16-bit polynomial i := 1 do {     if crc and 0x8000 {         crc := (crc leftShift 1) xor 0x1021 // The CRC polynomial     } else {         crc := crc leftShift 1     }     // crc is the value of big_endian_table[i]; let j iterate over the already-initialized entries for j from 0 to i−1 {big_endian_table[i + j] :=crc xor big_endian_table[j]; } i :=i <256 동안 1 }좌교대

코드 조각 7: 한 번에 바이트 수 CRC 테이블 생성, MSB 우선

little_endian_table[0] := 0 crc := 1; i := 128 do {     if crc and 1 {         crc := (crc rightShift 1) xor 0x8408 // The CRC polynomial     } else {         crc := crc rightShift 1     }     // crc is the value of little_endian_table[i]; let j iterate over the already-initialized entries for j from 0 to 255 by 2 × i {         little_endian_table[i + j] := crc xor little_endian_table[j]; } i := i := i 우측 변속 1 }, i > 0.

코드 조각 8: 바이트-at-time CRC 테이블 생성, LSB 우선

이 코드 샘플에서 테이블 인덱스는i + j와 같다i xor j; 당신은 어떤 형태든 더 편리한 것을 사용할 수 있다.

여러 테이블을 사용한 바이트 동기화

일반적으로 Sarwate 알고리즘과 비교하여 성능을 두 배 또는 세 배로 증가시키는 Slice-by-N(일반적으로 CRC32의 경우 슬라이스-by-8; N ≤ 64) 알고리즘이 존재한다.알고리즘은 한 번에 8비트를 읽는 대신 한 번에 8N비트를 읽는다.이렇게 하면 슈퍼스칼라 프로세서의 성능이 극대화된다.^[5]^[6]^[7]^[8]

누가 알고리즘을 실제로 발명했는지는 불분명하다.^[9]

테이블이 없는 병렬 계산

한 번에 바이트 또는 단어에 대한 병렬 업데이트도 테이블 없이 명시적으로 수행할 수 있다.^[10]이것은 보통 고속 하드웨어 구현에 사용된다.각 비트에 대해 8비트를 이동한 후 방정식이 해결된다.다음 표에는 다음 기호를 사용하여 일반적으로 사용되는 일부 다항식의 방정식이 나열되어 있다.

c_i	업데이트 전 CRC 비트 7…0(또는 15…0)
r_i	업데이트 후 CRC 비트 7…0(또는 15…0)
d_i	입력 데이터 비트 7…0
e_i = d_i + c_i	e_p = e₇ + e₆ + … + e₁ + e + e₀(입력 비트)
s_i = d_i + c_i+8	s_p = s₇ + s₆ + … + s + s₁₀ + s(입력 비트)

8비트가 이동된 후 일부 CRC-8 다항식에 대한 비트 업데이트 방정식
다항식:	(x⁷ + x³ + 1) x (좌측변형 CRC-7-CCITT)	x⁸ + x⁵⁴ + x + 1(CRC-8-Dallas/Maxim)
계수:	0x12 = (0x09 << 1)(MSBF/정상)	0x8c(LSBF/후진)
r₀ ← r₁ r₂ r r₃ r r₄ r r₅ r ← r ← r ← r₆₇ r	0 e₀ + e₄ + e₇₁ + e₅₂ + e + e₆₃₇ + e + e₀₄ + e + e + e₇₄ + e + e + e₁₅ + e + e₅ + e + e + e₂ + e + e + e₆ + e₆ + e + e + e + e + e + e + e + e₃ + e₇ + e	e₀ + e₄ + e₁ + e₅ + e₀₂ + e₁ + e₁₅ + e₂ + e₁ + e₆ + e + e₃ + e₂ + e₀₂ + e + e₆₃ + e₂ + e + e₀ + e + e₇ + e + e₄₃ + e + e₁₃ + e + e + e₀ + e₇ + e₄₃ + e + e + e₁₄ + e + e + e₁ + e + e₀₅ + e + e₂₁ + e + e + e₆ + e + e₃ + e₂ + e₀₇₄ + e + e + e + e + e + e + e + e + e + e + e + e + e + e + e + e + e + e + e + e + e + e + e + e + e₃ + e₁
C코드 조각:	uint8_t c, d, e, f, r; … e = c ^ d; f = e ^ (e >> 4) ^ (e >> 7); r = (f << 1) ^ (f << 4);	uint8_t c, d, e, f, r; … e = c ^ d; f = e ^ (e << 3) ^ (e << 4) ^ (e << 6); r = f ^ (f >> 4) ^ (f >> 5);

8비트 이동 후 일부 CRC-16 다항식에 대한 비트 업데이트 방정식
다항식:	x¹⁶¹² + x + x + 1⁵(CRC-16-CCITT)		x¹⁶¹⁵ + x + x + 1²(CRC-16-ANSI)
계수:	0x1021(MSBF/정상)	0x8408(LSBF/후진)	0x8005(MSBF/정상)	0xa001(LSBF/후진)
r₀ ← r₁ r₂₃ r r₄ r r₅ r r₆ r r₇ r r₈ r r₉ r ← r r₁₀ r r₁₁ r ← r ← r ← r ← ← r r₁₂₁₃ r r r r r r r r r r r r r₁₄ r r r r r₁₅ r	s₄ + s₀₅ + s + s₁₆₂₇ + s₃₄ + s₅ + s + s₄₀ + s₆ + s + s₅ + s₁₇ + s + s₀ + s₆₂ + s + s₇ + s₃₁ + s₄ + s₂ + s₅ + s₃ + s₆ + s₄ + s + s + s₇ + s + s₄₀ + s + s₅ + s₅ + s + s₁ + s₆ + s + s + s + s₆₂ + s + s₇ + s + s + s + s + s₇ + s + s + s + s + s + s + s + s₃ + s + s + s + s + s	c₈ + e₄ + e₀ + e₉ + e₅ + e₁₁₀₆ + e + e₂₁₁ + e₀ + e₇ + e + e₃₁₂ + e + e₁₁₃ + e₂ + e₁₄₃₁₅ + e₄₀ + e + e₀ + e + e₅ + e₁ + e₁₆ + e + e₂ + e₂ + e + e + e + e₇ + e₃ + e₃ + e + e + e + e + e₄ + e + e₀ + e₅ + e + e₁ + e + e + e + e₆₂₇ + e + e + e + e + e + e + e + e + e + e + e + e₃ + e	s_p₀_p + s_p + s₁₀ + s₁ + s₂₃ + s₄ + s₂₃ + s₅ + s₄₆ + s + s + s₅₀ + s + s + s₇ + s₁ + s₆ + s + s c₇ c₂₃₅ c₄₆₇ + s	c₈ + e_p c₉ c₁₀₁₁₁₂ c₁₃₁₄ + e₁₅ c₀ + e + e₁₀ + e₁ + e₂ + e₃ + e₄₅ + e₂₃ + e + e + e₄ + e + e₆ + e + e₅ + e + e + e + e + e₆ e₇ + e e_p + e e + e e + e + e₇ e_p e e + e e e + e
C코드 조각:	uint8_t d, s, t; uint16_t c, r; … s = d ^ (c >> 8); t = s ^ (s >> 4); r = (c << 8) ^ t ^ (t << 5) ^ (t << 12);	uint8_t d, e, f; uint16_t c, r; … e = c ^ d; f = e ^ (e << 4); r = (c >> 8) ^ (f << 8) ^ (f << 3) ^ (f >> 4);	uint8_t d, s, p; uint16_t c, r, t; … s = d ^ (c >> 8); p = s ^ (s >> 4); p = p ^ (p >> 2); p = p ^ (p >> 1); p = p & 1; t = p (s << 1); r = (c << 8) ^ (t << 15) ^ t ^ (t << 1);	uint8_t d, e, p; uint16_t c, r, f; … e = c ^ d; p = e ^ (e >> 4); p = p ^ (p >> 2); p = p ^ (p >> 1); p = p & 1; f = e (p << 8); r = (c >> 8) ^ (f << 6) ^ (f << 7) ^ (f >> 8);

2단계 연산

CRC-32 다항식에는 많은 수의 항이 있으므로, 나머지를 계산할 때 각 비트는 이전 반복의 몇 비트에 의존한다.바이트 병렬 하드웨어 구현에서 이는 다중 입력 또는 계단식 XOR 게이트를 요구하여 전파 지연을 증가시킨다.

연산 속도를 극대화하기 위해 123비트 시프트 레지스터를 통해 메시지를 전달하여 중간 나머지를 계산할 수 있다.다항식은 용어(피드백탭)의 간격이 넓도록 표준 다항식의 세심하게 선택된 배수로, 나머지 비트 중 어떤 비트도 바이트 반복당 한 번 이상 XOR로 처리되지 않는다.따라서 가능한 한 빨리 2입력 XOR 게이트만 있으면 된다.마지막으로 중간 나머지를 2교대 레지스터에서 표준 다항식으로 나누어 CRC-32 나머지를 산출한다.^[11]

원패스 체크

메시지에 CRC를 첨부할 때 전송된 CRC를 분리하여 다시 계산하고 전송된 CRC에 대해 다시 계산된 값을 확인할 수 있다.그러나 하드웨어에서는 더 간단한 기법이 일반적으로 사용된다.

CRC가 정확한 바이트 순서와 함께 전송될 때(선택한 비트 순서 지정 규약을 일치) 수신자는 메시지 및 CRC를 통해 전체 CRC를 계산할 수 있으며, CRC가 정확하다면 결과는 0이 된다.이러한 가능성은 CRC를 포함하는 대부분의 네트워크 프로토콜이 종료 구분 기호 이전에 그렇게 하는 이유다. CRC를 확인하기 위해 패킷의 끝이 임박했는지 알 필요는 없다.

CRC 변형

실제로 대부분의 표준은 레지스터의 사전 설정과 전송 전 CRC를 뒤집는 것을 명시한다.이것은 변경된 비트를 감지하는 CRC의 기능에는 영향을 미치지 않지만, 메시지에 추가된 비트를 알아차릴 수 있는 기능을 제공한다.

-1로 사전 설정

CRC의 기본 수학은 다항식으로 해석될 때 CRC 다항식의 배수인 메시지를 수용(올바른 전송으로 간주)한다.만일 일부 선행 0비트가 그러한 메시지에 선행된다면, 그것들은 다항식으로서의 해석을 바꾸지 않을 것이다.이는 0001과 1이 같은 숫자라는 사실과 맞먹는다.

그러나 전송되는 메시지가 선행 0비트에 신경을 쓴다면 기본 CRC 알고리즘이 그러한 변화를 감지하지 못하는 것은 바람직하지 않다.전송 오류가 그러한 비트를 추가할 수 있다면 간단한 해결책은rem0이 아닌 값으로 설정된 시프트 레지스터. 편리성을 위해 일반적으로 전체 원 값을 사용한다.이는 수학적으로 메시지의 첫 번째 n비트를 보완(이진 NOT)하는 것과 동등하며, 여기서 n은 CRC 레지스터의 비트 수입니다.

이는 발생기와 검사기가 모두 동일한 초기값을 사용하는 한 CRC 생성 및 어떤 방식으로든 점검에 영향을 주지 않는다.0이 아닌 어떤 초기 값이라도 괜찮고, 몇몇 표준에서는 비정상적인 값을 명시하지만,^[12] 모든 원 값(-2진수 2진수)은 단연코 가장 흔하다.1-통과 CRC 생성/체크는 사전 설정된 값에 관계없이 메시지가 정확할 때 여전히 0의 결과를 생성한다는 점에 유의하십시오.

반전후

비록 메시지 집합이 더 제한적이긴 하지만, 같은 종류의 오류가 메시지의 끝에서 발생할 수 있다.메시지에 0비트를 추가하는 것은 다항식을 x로 곱하는 것과 같으며, 만약 그것이 이전에 CRC 다항식의 배수였다면, 그 곱셈의 결과도 또한 될 것이다.이는 726이 11의 배수량이기 때문에 7260이 된다는 사실과 맞먹는다.

메시지가 첨부되기 전에 CRC 레지스터를 뒤집어서 메시지의 끝에 유사한 솔루션을 적용할 수 있다.다시 말해, 0이 아닌 어떤 변화도 가능하다; 모든 비트를 뒤집는 것이 가장 흔하다.

이것은 원패스 CRC 확인에 영향을 미친다: 메시지가 정확할 때 0의 결과를 생성하는 대신, 고정된 0이 아닌 결과를 산출한다. (정확히 말하면, 결과는 반전 패턴의 CRC(비 0 사전 설정 없이, 그러나 역반전 후)이다.일단 이 상수를 얻으면(임의의 메시지에서 원패스 CRC 생성/체크를 가장 쉽게 수행), 동일한 CRC 알고리즘을 사용하여 체크한 다른 메시지의 정확성을 직접 검증하는 데 사용할 수 있다.

참고 항목

일반분류

코드 수정 오류
해시함수 목록
패리티는 다항식 $x +1$ 의 1비트 CRC와 동일하다.

비 CRC 체크섬

참조

^ Dubrova, Elena; Mansouri, Shohreh Sharif (May 2012). "A BDD-Based Approach to Constructing LFSRs for Parallel CRC Encoding". Proceedings of IEEE International Symposium on Multiple-Valued Logic: 128–133. doi:10.1109/ISMVL.2012.20. ISBN 978-0-7695-4673-5. S2CID 27306826.
^ ^a ^b Williams, Ross N. (1996-09-24). "A Painless Guide to CRC Error Detection Algorithms V3.00". Archived from the original on 2006-09-27. Retrieved 2016-02-16.
^ Sarwate, Dilip V. (August 1998). "Computation of Cyclic Redundancy Checks via Table Look-Up". Communications of the ACM. 31 (8): 1008–1013. doi:10.1145/63030.63037. S2CID 5363350.
^ "Portable Network Graphics (PNG) Specification (Second Edition): Annex D, Sample Cyclic Redundancy Code implementation". W3C. 2003-11-10. Retrieved 2016-02-16.
^ Kounavis, Michael E.; Berry, Frank L. (27–30 June 2005). A Systematic Approach to Building High Performance, Software-based, CRC Generators (PDF). 2013 IEEE Symposium on Computers and Communications (ISCC). Cartagena, Murcia, Spain. pp. 855–862. doi:10.1109/ISCC.2005.18. ISBN 0-7695-2373-0.
^ Berry, Frank L.; Kounavis, Michael E. (November 2008). "Novel Table Lookup-Based Algorithms for High-Performance CRC Generation". IEEE Transactions on Computers. 57 (11): 1550–1560. doi:10.1109/TC.2008.85. S2CID 206624854.
^ High Octane CRC Generation with the Intel Slicing-by-8 Algorithm (PDF) (Technical report). Intel. Archived from the original (PDF) on 2012-07-22.
^ https://www.kernel.org/doc/Documentation/crc32.txt
^ Menon-Sen, Abhijit (2017-01-20). "Who invented the slicing-by-N CRC32 algorithm?".
^ Jon Buller (1996-03-15). "Re: 8051 and CRC-CCITT". Newsgroup: comp.arch.embedded. Usenet: 31498ED0.7C0A@nortel.com. Retrieved 2016-02-16.
^ Glaise, René J. (1997-01-20). "A two-step computation of cyclic redundancy code CRC-32 for ATM networks". IBM Journal of Research and Development. Armonk, NY: IBM. 41 (6): 705. doi:10.1147/rd.416.0705. Archived from the original on 2009-01-30. Retrieved 2016-02-16.
^ 예: 저주파 RFID

외부 링크

JohnPaul Adamovsky. "64 Bit Cyclic Redundant Code – XOR Long Division To Bytewise Table Lookup".

Andrew Kadarch, Bob Jenkins. "Efficient (~1 CPU cycle per byte) CRC implementation". GitHub.

[1] Dubrova, Elena; Mansouri, Shohreh Sharif (May 2012). "A BDD-Based Approach to Constructing LFSRs for Parallel CRC Encoding". Proceedings of IEEE International Symposium on Multiple-Valued Logic: 128–133. doi:10.1109/ISMVL.2012.20. ISBN 978-0-7695-4673-5. S2CID 27306826.

[williams96-2] Williams, Ross N. (1996-09-24). "A Painless Guide to CRC Error Detection Algorithms V3.00". Archived from the original on 2006-09-27. Retrieved 2016-02-16.

[3] Sarwate, Dilip V. (August 1998). "Computation of Cyclic Redundancy Checks via Table Look-Up". Communications of the ACM. 31 (8): 1008–1013. doi:10.1145/63030.63037. S2CID 5363350.

[4] "Portable Network Graphics (PNG) Specification (Second Edition): Annex D, Sample Cyclic Redundancy Code implementation". W3C. 2003-11-10. Retrieved 2016-02-16.

[5] Kounavis, Michael E.; Berry, Frank L. (27–30 June 2005). A Systematic Approach to Building High Performance, Software-based, CRC Generators (PDF). 2013 IEEE Symposium on Computers and Communications (ISCC). Cartagena, Murcia, Spain. pp. 855–862. doi:10.1109/ISCC.2005.18. ISBN 0-7695-2373-0.

[6] Berry, Frank L.; Kounavis, Michael E. (November 2008). "Novel Table Lookup-Based Algorithms for High-Performance CRC Generation". IEEE Transactions on Computers. 57 (11): 1550–1560. doi:10.1109/TC.2008.85. S2CID 206624854.

[7] High Octane CRC Generation with the Intel Slicing-by-8 Algorithm (PDF) (Technical report). Intel. Archived from the original (PDF) on 2012-07-22.

[8] ttps://www.kernel.org/doc/Documentation/crc32.txt

[9] Menon-Sen, Abhijit (2017-01-20). "Who invented the slicing-by-N CRC32 algorithm?".

[10] Jon Buller (1996-03-15). "Re: 8051 and CRC-CCITT". Newsgroup: comp.arch.embedded. Usenet: 31498ED0.7C0A@nortel.com. Retrieved 2016-02-16.

[glaise-11] Glaise, René J. (1997-01-20). "A two-step computation of cyclic redundancy code CRC-32 for ATM networks". IBM Journal of Research and Development. Armonk, NY: IBM. 41 (6): 705. doi:10.1147/rd.416.0705. Archived from the original on 2009-01-30. Retrieved 2016-02-16.

[12] 예: 저주파 RFID

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

Search