상수 쉬프

이 글은 검증을 위해 인용구가 추가로 필요하다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선할 수 있도록 도와주십시오. 공급되지 않은 재료는 도전하여 제거할 수 있다. 출처 찾기: "Constant sheaf" – 뉴스 · 신문 · 책 · 학자 · JSTOR (2010년 5월) (이 템플릿 메시지를 제거하는 방법과 시기 학습)

수학에서, 집합 A와 연관된 위상학적 공간 X의 상수 셰프는 X의 집합체인데, 줄기는 모두 A와 같다.A 또는 A로_X 표기되어 있다.값 A가 있는 상수 사전 준비는 X의 비어 있지 않은 각 부분 집합에 값 A를 할당하는 사전 준비 작업이며, 제한 지도가 모두 ID 맵 A → A이다.A와 연관된 상수 피복은 A와 연관된 상수 사전 피복이다.

특정한 경우에, 세트 A는 일부 범주 C에서 물체 A로 대체될 수 있다(예: C가 아벨리아 그룹 또는 역류 링의 범주인 경우).

아벨리아 집단의 지속적인 층은 특히 피복 코호몰로지 계수로 나타난다.

기본 사항

X는 위상학적 공간이고, A는 한 세트로 하자.오픈 세트 U에 대한 상수 피복 A의 섹션은 연속 함수 U → A에 이산 토폴로지가 주어지는 것으로 해석할 수 있다.U가 연결되면 이 국소 상수 기능이 일정하게 유지된다.f: X → {pt}이(가) 원포인트 공간에 대한 고유 맵이고 {pt}에서 A가 sheaf로 간주되는 경우, 역 이미지 fA는⁻¹ X의 상수 sheaf A이다.A의 sheaf 공간은 투영 지도 X × A → X (A에 이산 위상이 주어지는 곳)이다.

상세한 예

X를 이산 위상 p와 q 두 점으로 구성된 위상학적 공간이 되도록 한다.X에는 sets, {p}, {q}, {p, q}의 네 가지 오픈 세트가 있다.X의 오픈 세트의 비교 포함 5개가 차트에 표시된다.

X에 대한 사전 조사에서는 X의 네 가지 오픈 세트 각각에 대해 세트를 선택하고, 9가지 포함 요소 각각에 대한 제한 지도를 선택한다(비-비-비-비-비-비-비-비-비-비-비-비-비-비-비-비-비-비-비-비-비-비-비-비-비-비-)).우리가 F값을 나타낼 값 Z의 상수 프리슈프는 4세트를 모두 Z로, 정수, 모든 제한지도를 ID로 선택하는 프리슈프다.F는 일정하기 때문에 functor, 그러므로 presheaf이다.F는 접착 공리를 만족시키지만, 빈 세트에서 국부적 정체 공리를 실패하기 때문에 피복이 아니다.빈 세트는 빈 세트의 빈 패밀리에 의해 다루어지기 때문이다: 빈 세트 위에 있는 F의 어떤 두 구간도 빈 패밀리의 어떤 세트로 제한될 때 같기 때문이다.따라서 국부적 정체성 공리는 빈 집합에 대한 F의 어떤 두 섹션도 동일하다는 것을 암시할 수 있지만, 이것은 사실이 아니다.

빈 집합에 대한 로컬 ID 공리를 만족하는 유사한 사전 예시 G는 다음과 같이 구성된다.G(평균) = 0으로 두십시오. 여기서 0은 1-요소 집합입니다.비어 있지 않은 모든 집합에서 G에 Z 값을 부여하십시오.각 오픈 세트의 포함에 대해, G는, 작은 세트가 비어 있는 경우, 고유 맵을 0으로 되돌리거나, Z의 ID 맵을 반환한다.

빈 집합에 대한 로컬 ID 공리의 결과로 빈 집합과 관련된 모든 제한 지도가 지루하다는 점에 유의하십시오.이것은 빈 세트에 대한 지역 정체성 공리를 만족하는 모든 사전 조치와 특히 모든 피복에 적용된다.

G는 분리된 프리쉐프(즉, 국소 ID 공리를 만족함)이지만 F와 달리 접착 공리는 실패한다.{p, q}은(는) 두 개의 열린 집합 {p}과(와) {q}이(가) 포함되며 이 집합에는 빈 교차점이 있다.{p} 또는 {q}의 섹션은 Z의 요소, 즉 숫자다.{p} 이상의 섹션 m과 {q} 이상의 n을 선택하고 m ≠n을 가정하십시오. m과 n은 ∅ 이상의 동일한 요소 0으로 제한하므로, 접착 공리는 {p}의 경우 m을 제한하고 {q}의 경우 {p}의 경우 n을 제한하는 고유한 섹션 s가 있어야 한다.그러나 {p, q}에서 {p}까지의 제한 지도가 s = m이고, 이와 유사하게 s = n이므로 m = n, 모순이기 때문이다.

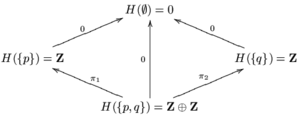
G({p, q})가 너무 작아서 {p}과(와) {q} 모두에 대한 정보를 전달할 수 없다.접착 공리를 만족하도록 확대하려면 H({p, q}) = Z ⊕ Z를 두십시오.π과₁ π을₂ 두 개의 투영 지도 Z ⊕ Z → Z가 되게 한다.H({p}) = 임(m₁) = Z 및 H({q}) = 임(m₂) = Z를 정의하십시오.나머지 오픈 세트 및 포함물에 대해서는 H가 G가 되도록 한다.H는 값 Z를 가진 X 위의 상수 깎기라고 불리는 껍질이다.Z는 반지이고 모든 제한지도는 고리 동형이기 때문에 H는 교감반지의 한 조각이다.

참고 항목

• 국소 상수 피복

참조

• 섹션 II.1 ofHartshorne, Robin (1977), Algebraic Geometry, Graduate Texts in Mathematics, vol. 52, New York: Springer-Verlag, ISBN 978-0-387-90244-9, MR 0463157
• 제2.4.6절