연속 저온 전차형 원자로

연속 저온 전차 원자로의 설정을 보여주는 다이어그램.

원자로 또는 백믹스 원자로, 혼합유량 원자로(MFR) 또는 연속유량 저온유량 탱크 원자로(CFTR)라고도 알려진 연속 저온조 탱크로(CTR)는 화학공학 및 환경공학에서 화학원자로의 일반적인 모델이다. CSR은 종종 연속적인 동요 탱크 원자로를 사용하여 지정된 출력에 도달할 때 주요 단위 운전 변수를 추정하는 데 사용되는 모델을 말한다. 그 수학 모델은 액체, 가스, 슬러리와 같은 모든 액체에 효과가 있다.

CSR의 동작은 종종 완벽한 혼합을 가정하는 이상적인 CSR의 동작에 의해 근사치되거나 모델링된다. 완벽하게 혼합된 원자로에서 시약은 진입 시 즉시 원자로 전체에서 균일하게 혼합된다. 따라서 출력 구성은 원자로 내부의 재료 구성과 동일하며, 이는 거주 시간과 반응률의 함수다. CSR은 플러그 유량 원자로(PFR)와 정반대인 원자로 설계에서 완전 혼합의 이상적인 한계다. 실제로 어떤 원자로도 이상적으로 작용하지 않고 대신에 이상적인 CSR과 PFR의 혼합 한계 사이에 있다.

이상적인 CSR

CSR의 단면도.

모델링.

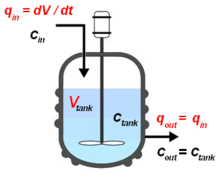
비보정 화학 반응제 A를 포함하는 연속 유체 흐름은 V 부피의 이상적인 CSR로 들어간다.

가정:

완벽하거나 이상적인 혼합
안정 상태 ${\Bigl (}{\frac {dN_{A}}{dt}}=0{\Bigr )}$ ${\Bigl (}{\frac {dN_{A}}{dt}}=0{\Bigr )}$ ${\Bigl (}{\frac {dN_{A}}{dt}}=0{\Bigr )}$ ${\Bigl (}{\frac {dN_{A}}{dt}}=0{\Bigr )}$ ${\Bigl (}{\frac {dN_{A}}{dt}}=0{\Bigr )}$ = ${\Bigl (}{\frac {dN_{A}}{dt}}=0{\Bigr )}$ ) ${\$ ${\Bigl (}{\frac {dN_{A}}{dt}}=0{\Bigr )}$ 여기서_A N은 A종의 두더지 수입니다.
폐쇄된 경계
일정한 유체 밀도(대부분의 액체에 유효함, 두더지 수의 순변동이나 급격한 온도 변화가 없는 경우에만 기체에 유효함)
n 순서^th 반응(r = kC) 여기서_Aⁿ k는 반응률 상수, C는_A 종 A의 농도, n은 반응 순서다.
등온 상태 또는 일정한 온도(k는 일정함)
되돌릴 수 없는 단일 반응(반복_A = -1)
모든 반응제 A는 화학반응을 통해 제품으로 전환된다.
N_A = C_A V

체적 V의 원자로에서 종 A의 점 N_A 수에 대한 적분 질량 균형 : 1. $1.[{\text{Net accumulation of}}~A]=[A~{\text{in}}]-[A~{\text{out}}]+[{\text{Net generation of}}~A]$ [ $1.[{\text{Net accumulation of}}~A]=[A~{\text{in}}]-[A~{\text{out}}]+[{\text{Net generation of}}~A]$ 의 순 $1.[{\text{Net accumulation of}}~A]=[A~{\text{in}}]-[A~{\text{out}}]+[{\text{Net generation of}}~A]$ $1.[{\text{Net accumulation of}}~A]=[A~{\text{in}}]-[A~{\text{out}}]+[{\text{Net generation of}}~A]$ = $1.[{\text{Net accumulation of}}~A]=[A~{\text{in}}]-[A~{\text{out}}]+[{\text{Net generation of}}~A]$ [ $1.[{\text{Net accumulation of}}~A]=[A~{\text{in}}]-[A~{\text{out}}]+[{\text{Net generation of}}~A]$ $1.[{\text{Net accumulation of}}~A]=[A~{\text{in}}]-[A~{\text{out}}]+[{\text{Net generation of}}~A]$ $1.[{\text{Net accumulation of}}~A]=[A~{\text{in}}]-[A~{\text{out}}]+[{\text{Net generation of}}~A]$ - $1.[{\text{Net accumulation of}}~A]=[A~{\text{in}}]-[A~{\text{out}}]+[{\text{Net generation of}}~A]$ [ A $1.[{\text{Net accumulation of}}~A]=[A~{\text{in}}]-[A~{\text{out}}]+[{\text{Net generation of}}~A]$ $1.[{\text{Net accumulation of}}~A]=[A~{\text{in}}]-[A~{\text{out}}]+[{\text{Net generation of}}~A]$ + $1.[{\text{Net accumulation of}}~A]=[A~{\text{in}}]-[A~{\text{out}}]+[{\text{Net generation of}}~A]$ [ $1.[{\text{Net accumulation of}}~A]=[A~{\text{in}}]-[A~{\text{out}}]+[{\text{Net generation of}}~A]$ $1.[{\text{Net accumulation of}}~A]=[A~{\text{in}}]-[A~{\text{out}}]+[{\text{Net generation of}}~A]$ 의 순 $1.[{\text{Net accumulation of}}~A]=[A~{\text{in}}]-[A~{\text{out}}]+[{\text{Net generation of}}~A]$ ] ${\displaystyle 1.$ $[{\text{{Net accumulation of}}~A]=$ $[A~{\text{in}}]-[A~{\text{out}}]+[{\text{net generation of}}~A]}$

$2번 화면.{\frac {dN_{A}}{dt}}=F_{Ao}-F_{{{Ao}-F_{{}}}{{dt}=F_{Ao}-{}}A}+V\nu _{A}r_{A}$ ^[1]

어디에

F는_Ao A종의 어금니 유량 유입구다.
F는_A A종의 어금니 유량 배출구다.
v는_A 계량계수다.
r은_A 반응률이다.

안정 상태와 ν_A = -1, 방정식 2의 가정을 적용하면 다음과 같은 것이 간단해진다.

$3.\ 0=F_{Ao}-F_{A}-Vr_{{A}A$

A종의 어금니 유량은 A의 농도와 유체 유량(Q):

$4.\ 0=QC_{Ao}-QC_{A}-Vr_{{A}A$ ^[2]

그런 다음 방정식 4를 다시 배열하여 r을_A 분리하고 단순화할 수 있다.

$5.\ r_{A}={\frac {Q}{V}}(C_{Ao}-C_{A})$ ^[2]

$6.\ r_{A}={\frac {1}{\1}{\tau }}}(C_{Ao}-C_{A})$

어디에

$【\displaystyle \tau 】}$ 이 $\tau$ (가) 이론적 거주 시간( $\tau ={\tfrac {V}{Q}}$ = $\tau ={\tfrac {V}{Q}}$ $\tau ={\tfrac {V}{Q}}$ ${\$
C는_Ao A종의 유입농도다.
C는_A A종의 원자로/배출구 농도다.

체류시간은 별도의 시약량이 원자로 내부에서 소비하는 총 시간이다. 이상적인 원자로의 경우 이론적 거주 시간인 $\tau$ ${\displaystyle \tau$ $\tau$ 은 원자로 부피를 유체 유량으로 나눈 값과 항상 같다.^[2] CSR의 거주 시간 분포에 대한 자세한 내용은 다음 절을 참조하십시오.

반응 순서에 따라 반응률 r은_A 일반적으로 원자로 내 종 A의 농도와 속도 상수에 따라 달라진다. CSR을 모델링할 때 핵심 가정은 유체 내 모든 반응제가 원자로에서 완벽하게 혼합(즉, 균일하게)된다는 것이며, 이는 원자로 내의 농도가 출구 흐름에서 동일하다는 것을 의미한다.^[3] 비율 상수는 아르헤니우스 온도 의존성을 사용하여 온도에 대해 조절되는 알려진 경험적 반응률을 사용하여 결정할 수 있다.^[2] 일반적으로 온도가 올라가면 반응이 일어나는 속도도 증가한다.

방정식 6은 적절한 비율 표현을 대체한 후 통합으로 해결할 수 있다. 아래 표는 이상적인 CSR을 위한 종 A의 배출구 농도를 요약한 것이다. 배출구 농도 및 거주 시간의 값은 산업용 응용을 위한 CSR 설계의 주요 설계 기준이다.

이상적인 CSR을 위한 배출구 농도
리액션 오더	C_A
n=0	$C_{A}={C_{Ao}-{k\tau }}$
n=1	$C_{A}={\frac {C_{Ao}{1+k\tau }}$ ^[1]
n=2	$C_{A}={\frac {-1+{\sqrt{1+4k\tau C_{Ao}}{2k\tau }}}$
기타 n	수치해결 필요

거주시간 분포

이상적인 CSR에 대한 종료 연령 분포 E(t) 및 누적 연령 분포 F(t) 함수.

이상적인 CSR은 원자로의 거주 시간 분포 또는 출구 연령 분포로 특징지을 수 있는 잘 정의된 흐름 동작을 보일 것이다.^[4] 모든 유체 입자가 원자로 내에서 동일한 시간을 소비하는 것은 아니다. 출구 연령 분포(E(t)는 주어진 유체 입자가 원자로에서 시간 t를 소비할 확률을 정의한다. 마찬가지로, 누적 연령 분포(F(t)는 주어진 유체 입자가 시간 t보다 적은 출구 연령을 가질 확률을 제공한다.^[3] 출구 연령 분포에서 중요한 도약점 중 하나는 극소수의 유체 입자가 CSR을 결코 빠져나가지 못한다는 것이다.^[5] 이는 원자로의 적용에 따라 자산이 될 수도 있고 단점이 될 수도 있다.

비이상적 CSR

이상적인 CSR 모델은 화학적 또는 생물학적 과정 동안 구성 요소의 운명을 예측하는 데 유용하지만, CSR은 현실에서 이상적인 행동을 보이는 경우가 거의 없다.^[2] 보다 일반적으로 원자로 유압 장치는 이상적으로 동작하지 않거나 시스템 조건이 초기 가정을 따르지 않는다. 완벽한 믹싱은 이론적인 개념으로, 실제로 달성될 수 없다.^[6] 그러나 엔지니어링 목적상 거주 시간이 혼합 시간의 5-10배인 경우, 완벽한 혼합 가정은 일반적으로 유효하다.

사공간이 있는 CSR에 대한 종료 연령 분포 E(t) 및 누적 연령 분포 F(t) 함수.

비이상적인 유압 작용은 일반적으로 사체 공간이나 단락 회로에 의해 분류된다. 이러한 현상은 일부 유체가 이론적 거주 시간보다 ~~$\tau$~~ 에서 더 적은 시간을 소비할 때 발생한다 ~~$\tau$~~ 원자로에 코너나 ~~$배플$~~ 이 있으면 유체가 잘 섞이지 않는 일부 사공간이 되는 경우가 많다.^[6] 마찬가지로, 원자로 내의 유체 분사도 단락을 유발할 수 있으며, 이 경우 흐름의 일부가 벌크 유체보다 훨씬 빨리 원자로를 빠져나간다. CSR에서 사체 공간이나 단락이 발생하는 경우, 관련 화학적 또는 생물학적 반응은 액체가 원자로를 빠져나가기 전에 완료되지 않을 수 있다.^[2] 이상 흐름으로부터의 일탈은 오른쪽에서 보이는 이상적인 분포와 다른 거주 시간 분포를 초래할 것이다.

비이상적 흐름 모델링

이상적인 유량 원자로는 실제로 거의 발견되지 않지만, 비이상적인 유량 원자로를 모델링하는 데 유용한 도구다. 모든 흐름 체계는 원자로를 직렬 또는 병렬로 이상적인 CSR과 플러그 유량 원자로(PFR)의 조합으로 모델링하여 달성할 수 있다.^[6] 예를 들어, 이상 CSR의 무한 시리즈는 유압학적으로 이상 PFR과 동등하다.^[2] 직렬로 된 다수의 CSR을 결합한 원자로 모델을 흔히 TIS(tank-in-series) 모델이라고 부른다.^[7]

일정한 온도 및 단일 반응의 가정에 따르지 않는 시스템을 모델링하려면 추가 종속 변수를 고려해야 한다. 시스템이 불안정 상태로 간주되는 경우, 미분 방정식 또는 결합된 미분 방정식의 시스템을 해결해야 한다. CSR 거동의 편차는 분산 모델에 의해 고려될 수 있다. CSR은 정상 상태 다중성, 한계 주기, 혼돈과 같은 복잡한 행동을 보이는 시스템 중 하나로 알려져 있다.

계단식 CSR

일련의 세 개의 CSR

일련의 CSR로도 알려진 CSR의 계단식들은 시스템의 볼륨을 감소시키는데 사용된다.^[8]

볼륨 최소화

연속적으로 CSR의 수가 증가하면 전체 원자로 용량은 감소한다.

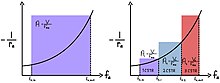
1개의 CSR을 가진 그래프에서 보듯이, 역률이 분수 변환 함수로 표시되며, 상자 내 면적은 ${\frac {V}{F_{Ao}}}$ ${\frac {V}{F_{Ao}}}$ ${\frac {V}{F_{Ao}}}$ ${\frac {V}{F_{Ao}}}$ ${\$ 과 같으며 ${\frac {V}{F_{Ao}}}$ , 여기서 V는 총 원자로 $F_{Ao}$ 이고 $F_{Ao}$ A $F_{Ao}$ {\ $displaysty F_{Ao}}}}}$ 은 공급의 어금간 유속이다 $F_{Ao}$ . 3개의 CSR이 있는 그래프에서 볼 수 있는 것과 같은 단계적 CSR에 동일한 공정을 적용하면 각 원자로의 부피는 각 입구와 출구 부분 변환에서 계산되어 총 원자로 부피가 감소한다. 최적 크기는 이전에 단일 CSR로 덮었던 직렬로 된 CSR에서 직사각형 위의 영역이 최대화되었을 때 달성된다. 2개의 CSR을 사용한 첫 번째 주문 반응의 경우 동일한 볼륨을 사용해야 한다. 이상적인 CSR (n)의 수가 무한대에 근접함에 따라, 총 원자로 용적은 동일한 반응과 부분 변환을 위한 이상적인 PFR의 용량에 접근한다.

CSR의 이상적인 캐스케이드

c = $\tau ={\frac {C_{Ao}-C_{A}}{-r_{A}}}$ A $\tau ={\frac {C_{Ao}-C_{A}}{-r_{A}}}$ - $\tau ={\frac {C_{Ao}-C_{A}}{-r_{A}}}$ A $\tau ={\frac {C_{Ao}-C_{A}}{-r_{A}}}$ - r $\tau ={\frac {C_{Ao}-C_{A}}{-r_{A}}}$ ${\$ A}}}}}{-r_{}}}}{\displaystysty style \cH00} $A}}}},$ $\tau _{i}={\frac {C_{A(i-1)}-C_{Ai}}{-r_{Ai}}}$ $\tau _{i}={\frac {C_{A(i-1)}-C_{Ai}}{-r_{Ai}}}$ = $\tau _{i}={\frac {C_{A(i-1)}-C_{Ai}}{-r_{Ai}}}$ A $\tau _{i}={\frac {C_{A(i-1)}-C_{Ai}}{-r_{Ai}}}$ ( $\tau _{i}={\frac {C_{A(i-1)}-C_{Ai}}{-r_{Ai}}}$ - $\tau _{i}={\frac {C_{A(i-1)}-C_{Ai}}{-r_{Ai}}}$ ) $\tau _{i}={\frac {C_{A(i-1)}-C_{Ai}}{-r_{Ai}}}$ - $\tau _{i}={\frac {C_{A(i-1)}-C_{Ai}}{-r_{Ai}}}$ $\tau _{i}={\frac {C_{A(i-1)}-C_{Ai}}{-r_{Ai}}}$ $\tau _{i}={\frac {C_{A(i-1)}-C_{Ai}}{-r_{Ai}}}$ - r $\tau _{i}={\frac {C_{A(i-1)}-C_{Ai}}{-r_{Ai}}}$ ${\$ 을(으) 직렬로 확인할 수 있다.

여기서 $\tau$ 는 $\tau$ 원자로의 공간시간이고, $C_{Ao}$ $C_{A}$ $C_{Ao}$ ${\$ 는 $C_{Ao}$ A의 공급농도, $C_{A}$ A ${\$ 는 $C_{A}$ A의 배출농도, $-r_{A}$ - $-r_{A}$ ${\$ 는 $-r_{A}$ A의 반응률이다.

퍼스트 오더

등온 첫 번째 순서의 경우, 정상 상태에서 작동하는 동일한 CSR의 계단식에서의 일정한 밀도 반응

1CTR: $C_{A1}={\frac {C_{Ao}}{1+k\tau }}$ $C_{A1}={\frac {C_{Ao}}{1+k\tau }}$ $C_{A1}={\frac {C_{Ao}}{1+k\tau }}$ = $C_{A1}={\frac {C_{Ao}}{1+k\tau }}$ A $C_{A1}={\frac {C_{Ao}}{1+k\tau }}$ $C_{A1}={\frac {C_{Ao}}{1+k\tau }}$ + $C_{A1}={\frac {C_{Ao}}{1+k\tau }}$ $C_{A1}={\frac {C_{Ao}}{1+k\tau }}$ ${\$ $C_{A1}={\frac {C_{Ao}}{1+k\tau }}$ 여기서 k는 속도 상수이고 $C_{A1}$ A ${\$ 는 첫 번째 CSTR에서 A의 배출구 농도다 $C_{A1}$ .

Two CSTRs: $C_{A1}={\frac {C_{Ao}}{1+k\tau }}$ and $C_{A2}={\frac {C_{A1}}{1+k\tau }}$

첫 번째 CSR 방정식을 두 번째에 연결: $C_{A2}={\frac {C_{Ao}}{(1+k\tau )^{2}}}$ $C_{A2}={\frac {C_{Ao}}{(1+k\tau )^{2}}}$ $C_{A2}={\frac {C_{Ao}}{(1+k\tau )^{2}}}$ = C $C_{A2}={\frac {C_{Ao}}{(1+k\tau )^{2}}}$ $C_{A2}={\frac {C_{Ao}}{(1+k\tau )^{2}}}$ ( 1 $C_{A2}={\frac {C_{Ao}}{(1+k\tau )^{2}}}$ + $C_{A2}={\frac {C_{Ao}}{(1+k\tau )^{2}}}$ $C_{A2}={\frac {C_{Ao}}{(1+k\tau )^{2}}}$ ) $C_{A2}={\frac {C_{Ao}}{(1+k\tau )^{2}}}$ ${\$ Ao}}}{( $1+k\tau )^{2}}:$

따라서 직렬로 동일한 CTR m의 경우: $C_{Am}={\frac {C_{Ao}}{(1+k\tau )^{m}}}$ $C_{Am}={\frac {C_{Ao}}{(1+k\tau )^{m}}}$ $C_{Am}={\frac {C_{Ao}}{(1+k\tau )^{m}}}$ = $C_{Am}={\frac {C_{Ao}}{(1+k\tau )^{m}}}$ $C_{Am}={\frac {C_{Ao}}{(1+k\tau )^{m}}}$ $C_{Am}={\frac {C_{Ao}}{(1+k\tau )^{m}}}$ ( 1 $C_{Am}={\frac {C_{Ao}}{(1+k\tau )^{m}}}$ + $C_{Am}={\frac {C_{Ao}}{(1+k\tau )^{m}}}$ $C_{Am}={\frac {C_{Ao}}{(1+k\tau )^{m}}}$ ) $C_{Am}={\frac {C_{Ao}}{(1+k\tau )^{m}}}$ ${\$

개별 CSR의 체적이 직렬로 변동하는 경우, CSR의 순서는 CSR이 동일한 온도에서 실행되는 한 첫 번째 주문 반응에 대한 전체 변환을 변경하지 않는다.

제롯순

안정상태에서 CSR의 계단식에서의 등온 제롯 주문반응에 대한 일반 방정식은 $C_{Am}=C_{Ao}-\sum _{i=1}^{m}k_{i}\tau _{i}$ $C_{Am}=C_{Ao}-\sum _{i=1}^{m}k_{i}\tau _{i}$ $C_{Am}=C_{Ao}-\sum _{i=1}^{m}k_{i}\tau _{i}$ = C $C_{Am}=C_{Ao}-\sum _{i=1}^{m}k_{i}\tau _{i}$ $C_{Am}=C_{Ao}-\sum _{i=1}^{m}k_{i}\tau _{i}$ - $C_{Am}=C_{Ao}-\sum _{i=1}^{m}k_{i}\tau _{i}$ i $C_{Am}=C_{Ao}-\sum _{i=1}^{m}k_{i}\tau _{i}$ = $C_{Am}=C_{Ao}-\sum _{i=1}^{m}k_{i}\tau _{i}$ m $C_{Am}=C_{Ao}-\sum _{i=1}^{m}k_{i}\tau _{i}$ { $C_{Am}=C_{Ao}-\sum _{i=1}^{m}k_{i}\tau _{i}$ ${\$ {i}}-}에 $의해 주어진다.$

CSR의 캐스케이드가 동일한 원자로와 등온일 때, 농도는 C $C_{Am}=C_{Ao}-mk_{i}\tau _{i}$ m $C_{Am}=C_{Ao}-mk_{i}\tau _{i}$ = $C_{Am}=C_{Ao}-mk_{i}\tau _{i}$ - $C_{Am}=C_{Ao}-mk_{i}\tau _{i}$ $C_{Am}=C_{Ao}-mk_{i}\tau _{i}$ $C_{Am}=C_{Ao}-mk_{i}\tau _{i}$ i $C_{Am}=C_{Ao}-mk_{i}\tau _{i}$ $C_{Am}=C_{Ao}-mk_{i}\tau _{i}$ ${\$ 에 의해 주어진다.

두 번째 순서

For an isothermal second order reaction at steady state in a cascade of CSTRs, the general design equation is $C_{Ai}={\frac {-1+{\sqrt {1+4k_{i}\tau _{i}C_{A(i-1)}}}}{2k_{i}\tau _{i}}}$

CSR의 비정상 계단식 계단식

비이상형 원자로에서는 거주 시간 분포를 계산할 수 있다. 직렬로 된 j번째 원자로의 농도에는 다음이 주어진다.

${\frac {C_{j}}{C_{o}}=1-e^{-{\frac {nt}{\bar{t}}}}[1+{\frac {nt}{\bar{t}}}}}+{\frac {1}{1}{2}!}}}}{\frac {nt}{\bar {t}}^{2}+...+{\frac {1}{(j-1)!}}}{\frac {nt}{\bar {t}}^{j-1}}$

여기서 n은 직렬의 총 CSR 수이며 ${\bar {t}}$ ${\$ {\bar ${t}}$ 은(는) ${\bar {t}}={\frac {V}{Q}}$ = V ${\bar {t}}={\frac {V}{Q}}$ ${\$ }={\ $frac {V}{$ Q}}}}이(가) 주어진 계단식 평균 거주 시간이며 ${\bar {t}}$ , 여기서 ${\bar {t}}={\frac {V}{Q}}$ Q는 체적 유량이다.

이를 통해 누적 거주 시간 분포(F(t))를 다음과 같이 계산할 수 있다.

$F(t)={\frac {C_{n}}{C_{{n}}}=1-e^{-{\frac {nt}{t}}}}[1+{\frac {nt}{\t}}}+{\frac {1}{1}:{2!}}}}{\frac {nt}{\bar {t}}^{2}+...+{\frac {1}{(n-1)!}}}{\frac {nt}{\bar {t}}^{n-1}}$

n → ∞로서 F(t)는 이상적인 PFR 응답에 접근한다. CSR의 계단식 펄스 자극에 대한 F(t)와 관련된 분산은 $\sigma _{t}^{2}={\frac {{\bar {t}}^{2}}{n}}$ t $\sigma _{t}^{2}={\frac {{\bar {t}}^{2}}{n}}$ = $\sigma _{t}^{2}={\frac {{\bar {t}}^{2}}{n}}$ 의 $\sigma _{t}^{2}={\frac {{\bar {t}}^{2}}{n}}$ {\ $displaystyle \sigma _{t}^{2}={\frac {{\bar{t}^{n$

비용

처음에는 부피가 감소함에 따라 CSR의 수에 따라 비용이 감소하지만, 운영 비용이 증가함에 따라 결국 총 비용은 증가하기 시작한다.

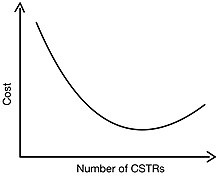
일련의 CSR의 비용을 결정할 때 자본 비용과 운영 비용을 고려해야 한다. 위에서 살펴본 바와 같이 직렬로 된 CSR의 수가 증가하면 전체 원자로 부피가 감소할 것이다. 물량에 따라 비용 규모가 커지기 때문에 CSR을 늘리면 자본 비용이 낮아진다. 가장 큰 비용 감소, 즉 부피 감소는 단일 CSR과 직렬로 두 개의 STR 사이에서 발생한다. 운영비를 고려할 때, 더 큰 폭포와 동반되는 펌프와 제어장치, 시공, 설치 및 유지보수의 수에 따라 운영비가 조정된다. 따라서 CSR의 수가 증가할수록 운영비는 증가한다. 따라서, 계단식 CSR과 관련된 최소 비용이 있다.

제롯 주문 반응

From a rearrangement of the equation given for identical isothermal CSTRs running a zeroth order reaction: $\tau ={\frac {C_{Ao}-C_{Am}}{mk}}$ , the volume of each individual CSTR will scale by ${\frac {1}{m}}$ . Therefore the total reactor volume is independent 제롯 주문 반응에 대한 CSR의 수. 따라서 원가는 제로 주문 반응에 대한 원자로 수의 함수가 아니며, CSR의 수가 증가해도 감소하지 않는다.

병렬 반응의 선택성

병렬 반응을 고려할 때, CSR의 계단식 활용은 원하는 제품의 선택성을 높일 수 있다.

주어진 평행하게 반응 들어 A⟶ B{\displaystyle{\ce{A->, B}}}과 ⟶ C{\displaystyle{\ce{A->, C}}}상수 k1{\displaystyle k_{1}}이고, k2{\displaystyle k_{2}}와 비율은 방정식 친절[B]dt=k1[A]n1{\displaystyle{\frac{d[{\ce{B}}]}{dt}}=k_.{1}[{) $ce {A}}]^{n_{1}}}$ and ${\frac {d[{\ce {C}}]}{dt}}=k_{2}[{\ce {A}}]^{n_{2}}$ , respectively, we can obtain a relationship between the two by dividing ${\frac {d[{\ce {B}}]}{dt}}$ by ${\displaystyle {\f$ $rac {d[{\ce{C}}}{dt$ 따라서}}. 경우 n1>n2{\displaystyle n_{1}>, n_{2}}와 B은 원하는 제품, CSTRs의 한 fre를 선택은[B]d[C])k1k2[A]n1− n2{\displaystyle{\frac{d[{\ce{B}}]}{d[{\ce{C}}]}}={\frac{k_{1}}{k_{2}}}[{\ce{A}}]^{n_{1}-n_{2}거라고 말했다.의심sh ${\ce {A}}$ ${\$ ${\ce {A}$ 의 농도를 극대화하기 위해 ${\ce {A}}$ A ${\$ displaystyle ${\ce {A}$ 의 콘도리 피드 ${\ce {A}}$

A+D⟶ B{\displaystyle{\ce{A+D->, B}}} 같은 2개 혹은 그 이상의 reactants와 A+D⟶ C{\displaystyle{\ce{A+D->, C}과 동시 반응 들어}}상수 k1{\displaystyle k_{1}}이고, k2{\displaystyle k_{2}}과 세율을 적용 해야[B]dt=k1[A]n1[. D] ${\frac {d[{\ce {B}}]}{dt}}=k_{1}[{\ce {A}}]^{n_{1}}[{\ce {D}}]^{m_{1}}$ and ${\frac {d[{\ce {C}}]}{dt}}=k_{2}[{\ce {A}}]^{n_{2}}[{\ce {D}}]^{m_{1}2}$ , respectively, we can obtain a relationship between the two by dividing ${\frac {d[{\ce {B}}]}{dt}}$ [ ${\frac {d[{\ce {B}}]}{dt}}$ ${\frac {d[{\ce {B}}]}{dt}}$ ${\frac {d[{\ce {B}}]}{dt}}$ ${\$ frac { $d[{\ce {B}]}{dt}}$ by ${\frac {d[{\ce {B}}]}{dt}}$ ${\frac {d[{\ce {C}}]}{dt}}$ [ ${\frac {d[{\ce {C}}]}{dt}}$ ${\frac {d[{\ce {C}}]}{dt}}$ t ${\$ frac ${d[{\ce {C}}}}{dt$ 따라서}}.[B]d[C])k1k2[A]n1− n2[D]m1− m2{\displaystyle{\frac{d[{\ce{B}}]}{d[{\ce{C}}]}}={\frac{k_{1}}{k_{2}}}[{\ce{A}}]^{n_{1}-n_{2}}[{\ce{D}}]^{m_{1}-m_{2} 해야에섰던 n1>n2{\displaystyle n_{1}>, n_{2}}과 m1&.gt;입니다 나이 $m_{1}>m_{2}$ ${\$ B는 $m_{1}>m_{2}$ 원하는 제품으로, 높은 ${\ce {[A]}}$ [ $]{\$ ${[A$ $]},$ ${\ce {[D]}}$ [ ${\ce {[D]}}$ $]{\d}}}$ 의 ${\ce {[A]}}$ 유입 스트림을 가진 계단식 CSTR이 선호된다 ${\ce {[D]}}$ . 경우 n1>n2{\displaystyle n_{1}>, n_{2}}과 m 1<>m2{\displaystyle m_{1}<, m_{2}}와 D{\displaystyle{\ce{D}의 사료와 작은 2차 하천}에 B가 원하는 제품, CSTRs의{\displaystyle{\ce{A}이 밀집된 캐스케이드}}}를 받고 있다.[9]

그 CSTR 준 뒤 혼합 A⟶ B⟶ C{\displaystyle{\ce{A-&gt의;->, C}}} 같은 시리즈 반응 또한}}, C{\displaystyle{\ce{C}}}지만 원하는 제품은 B{\displaystyle{\ce{B}CSTRs 일반적으로 일반적으로}선택하지 않습니다}B{\displaystyle{\ce{B}사이의 선택도 가지고 있다. c ${\displaystyle {\ce{C$ 일반적으로 이러한 반응에 대해 배치형 원자로나 PFR을 선택한다.

적용들

CSR은 혼합을 통해 시약의 신속한 희석을 촉진한다. 따라서 무질서 반응의 경우 원자로 내 시약 농도가 낮다는 것은 STR이 동일한 체류시간을 갖는 PFR에 비해 시약 제거에 덜 효율적이라는 것을 의미한다.^[3] 따라서, CSR은 일반적으로 PFR보다 크며, 공간이 제한된 애플리케이션에서는 어려움이 될 수 있다. 그러나, CSR의 희석 효과의 추가 이점 중 하나는 시스템에 대한 충격을 중화시키는 능력이다. PFR과 반대로, CSR의 성능은 영향을 받는 구성의 변화에 덜 민감하므로 다음과 같은 다양한 산업 용도에 이상적이다.

브루클린 그린포인트에 있는 뉴타운 크릭 오수처리장의 혐기성 발굴자들.

환경공학

폐수처리용^[2] 슬러지 활성화 공정
자연폐수처리용^[2] 석호처리시스템
폐수 바이오솔리드^[10] 안정화를 위한 혐기성 디제스터
폐수 및 폭우수 유출에^[11] 대한 처리 습지

화학공학

제약 생산을^[12] 위한 루프 원자로

발효^[12]
바이오가스 생산

참고 항목

메모들

참조

^ ^a ^b Schmidt, Lanny D. (1998). The Engineering of Chemical Reactions. New York: Oxford University Press. ISBN 0-19-510588-5.
^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ Metcalf & Eddy (2013-09-03). Wastewater engineering : treatment and resource recovery. Tchobanoglous, George,, Stensel, H. David,, Tsuchihashi, Ryujiro,, Burton, Franklin L. (Franklin Louis), 1927-, Abu-Orf, Mohammad,, Bowden, Gregory (Fifth ed.). New York, NY. ISBN 978-0-07-340118-8. OCLC 858915999.
^ ^a ^b ^c Benjamin, Mark M. (2013-06-13). Water quality engineering : physical/chemical treatment processes. Lawler, Desmond F. Hoboken, New Jersey. ISBN 978-1-118-63227-7. OCLC 856567226.
^ Bolin, Bert; Rodhe, Henning (January 1973). "A note on the concepts of age distribution and transit time in natural reservoirs". Tellus. 25 (1): 58–62. doi:10.3402/tellusa.v25i1.9644. ISSN 0040-2826.
^ Monsen, Nancy E.; Cloern, James E.; Lucas, Lisa V.; Monismith, Stephen G. (September 2002). "A comment on the use of flushing time, residence time, and age as transport time scales". Limnology and Oceanography. 47 (5): 1545–1553. Bibcode:2002LimOc..47.1545M. doi:10.4319/lo.2002.47.5.1545.
^ ^a ^b ^c Davis, Mark E. (2003). Fundamentals of chemical reaction engineering. Davis, Robert J. (International ed.). Boston: McGraw-Hill. ISBN 978-1-62870-437-2. OCLC 880604539.
^ Stokes, R. L.; Nauman, E. Bruce (1970). "Residence Time Distribution Functions for Stirred Tanks in Series". Canadian Journal of Chemical Engineering. 48 (6): 723–725.
^ Hill, Charles G.; Root, Thatcher W. (2014). Introduction to Chemical Engineering Kinetics and Reactor Design, Second Edition. Hoboken, new Jersey: Wiley. pp. 241–253, 349–358. ISBN 9781118368251.
^ Levenspiel, Octave (1998). Chemical Reaction Engineering, 3rd Edition. Wiley. ISBN 978-0-471-25424-9.
^ Hurtado, F.J.; Kaiser, A.S.; Zamora, B. (March 2015). "Fluid dynamic analysis of a continuous stirred tank reactor for technical optimization of wastewater digestion". Water Research. 71: 282–293. doi:10.1016/j.watres.2014.11.053. ISSN 0043-1354. PMID 25635665.
^ Kadlec, Robert H.; Wallace, Scott D. (2009). Treatment Wetlands (second ed.). Boca Raton, FL, USA: CRC Press. p. 181. ISBN 978-1-56670-526-4.
^ ^a ^b "Visual Encyclopedia of Chemical Engineering". encyclopedia.che.engin.umich.edu. Retrieved 2020-04-30.

[Schmidt2-1] Schmidt, Lanny D. (1998). The Engineering of Chemical Reactions. New York: Oxford University Press. ISBN 0-19-510588-5.

[:122-2] ^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ Metcalf & Eddy (2013-09-03). Wastewater engineering : treatment and resource recovery. Tchobanoglous, George,, Stensel, H. David,, Tsuchihashi, Ryujiro,, Burton, Franklin L. (Franklin Louis), 1927-, Abu-Orf, Mohammad,, Bowden, Gregory (Fifth ed.). New York, NY. ISBN 978-0-07-340118-8. OCLC 858915999.

[:02-3] Benjamin, Mark M. (2013-06-13). Water quality engineering : physical/chemical treatment processes. Lawler, Desmond F. Hoboken, New Jersey. ISBN 978-1-118-63227-7. OCLC 856567226.

[4] Bolin, Bert; Rodhe, Henning (January 1973). "A note on the concepts of age distribution and transit time in natural reservoirs". Tellus. 25 (1): 58–62. doi:10.3402/tellusa.v25i1.9644. ISSN 0040-2826.

[5] Monsen, Nancy E.; Cloern, James E.; Lucas, Lisa V.; Monismith, Stephen G. (September 2002). "A comment on the use of flushing time, residence time, and age as transport time scales". Limnology and Oceanography. 47 (5): 1545–1553. Bibcode:2002LimOc..47.1545M. doi:10.4319/lo.2002.47.5.1545.

[:1-6] Davis, Mark E. (2003). Fundamentals of chemical reaction engineering. Davis, Robert J. (International ed.). Boston: McGraw-Hill. ISBN 978-1-62870-437-2. OCLC 880604539.

[7] Stokes, R. L.; Nauman, E. Bruce (1970). "Residence Time Distribution Functions for Stirred Tanks in Series". Canadian Journal of Chemical Engineering. 48 (6): 723–725.

[8] Hill, Charles G.; Root, Thatcher W. (2014). Introduction to Chemical Engineering Kinetics and Reactor Design, Second Edition. Hoboken, new Jersey: Wiley. pp. 241–253, 349–358. ISBN 9781118368251.

[9] Levenspiel, Octave (1998). Chemical Reaction Engineering, 3rd Edition. Wiley. ISBN 978-0-471-25424-9.

[10] Hurtado, F.J.; Kaiser, A.S.; Zamora, B. (March 2015). "Fluid dynamic analysis of a continuous stirred tank reactor for technical optimization of wastewater digestion". Water Research. 71: 282–293. doi:10.1016/j.watres.2014.11.053. ISSN 0043-1354. PMID 25635665.

[11] Kadlec, Robert H.; Wallace, Scott D. (2009). Treatment Wetlands (second ed.). Boca Raton, FL, USA: CRC Press. p. 181. ISBN 978-1-56670-526-4.

[:2-12] "Visual Encyclopedia of Chemical Engineering". encyclopedia.che.engin.umich.edu. Retrieved 2020-04-30.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[10]

[11]

[12]

Search