피복 그래프

Covering graph

그래프 이론의 수학적 학문에서, 그래프 C는 C의 꼭지점 집합에서 G의 꼭지점 집합까지 커버 맵이 있는 경우 다른 그래프 G의 커버 그래프를 말한다. 커버 맵 f는 추론이고 국소 이형성: C의 꼭지점 v의 인접성은 G의 f(v)의 인접성에 객관적으로 매핑된다.

리프트라는 용어는 종종 연결된 그래프의 커버 그래프의 동의어로 사용된다.

오해가 있을 수 있지만, 그래프와 꼭지점 커버 또는 가장자리 커버 사이에는 (확실한) 관계가 없다.

표지의 그래프의 조합형식은 다문자의 경우로 즉시 일반화된다.만약 우리가 1차원 세포단지를 가진 다문체를 식별한다면, 커버 그래프는 위상학적 공간의 공간을 커버하는 특별한 예에 불과하므로, 공간 커버 이론의 용어인 변환 그룹, 범용 커버, 아벨리안 커버 및 최대 아벨리안 커버를 사용할 수 있다.[1]

정의

G = (V1, E1)와 C = (V2, E2)를 두 개의 그래프로 하고, f: V → V를21 추론한다.그 다음 f는 각2 v f V에 대해, v의 인접성에 대한 f의 제한은 G의 f(v)의 인접성에 대한 편향이라면 C에서 G까지의 커버 맵이다. 그렇지 않으면, f는 입사된 엣지를 v의 일대일 에지 사건에 대한 f(v)에 매핑한다.

C에서 G까지의 커버 맵이 존재하는 경우, C는 커버 그래프 또는 G의 리프트가 된다.h 리프트는 커버 맵 f가 G의 모든 꼭지점 v에 대해 그것의 섬유 f−1(v)가 정확히 h 요소를 갖는 특성을 갖는 리프트다.

예

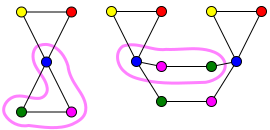
다음 그림에서, 그래프 C는 그래프 H의 커버 그래프 입니다.

Covering-graph-4.svg

C에서 H까지의 커버 맵 f는 색상으로 표시된다.예를 들어, C의 두 파란색 꼭지점은 모두 H의 파란색 꼭지점에 매핑된다.지도 f는 추론이다: H의 각 꼭지점에는 C에 프리이미지가 있다.더욱이, f는 객관적으로 C에서 정점 v의 각 인접성을 H에서 정점 f(v)의 인접성에 매핑한다.

예를 들어, v를 C의 보라색 꼭지점 중 하나로 두 개의 이웃, 녹색 꼭지점 u와 파란색 꼭지점 t가 있다.마찬가지로, v′는 H의 보라색 꼭지점이 되게 하고, H에는 녹색 꼭지점 u과 파란색 꼭지점 t′ 두 개의 이웃이 있다.{t, u, v}로 제한된 매핑 f는 {t f, u′, v′}에 대한 바이어싱입니다.이는 다음 그림에 설명되어 있다.

Covering-graph-4-a.svg

마찬가지로, 우리는 C에서 파란색 꼭지점의 인접성이 H:에서 파란색 꼭지점의 인접성에 일대일로 매핑되어 있는지 확인할 수 있다.

Covering-graph-4-b.svg

더블커버

위의 예에서 H의 각 꼭지점에는 C에 정확히 2개의 전치가 있다.따라서 C는 H의 2배 커버 또는 이중 커버다.

어떤 그래프 G의 경우, G의 쌍방향 이중표지, 즉 초당적 그래프와 G의 이중표지인 G의 쌍방향 표지를 구성할 수 있다.G의 초당적 이중 커버는 그래프 G × K2:의 텐서 곱이다.

Covering-graph-2.svg

G가 이미 초당적이라면, 그것의 초당적 이중 커버는 G의 두 개의 분리된 복사본으로 구성되어 있다. 그래프는 초당적 이중 커버를 제외하고 많은 다른 이중 커버를 가질 수 있다.

유니버설 커버

연결된 그래프 G의 경우 범용 표층 그래프를 구성할 수 있다.[2]이것은 위상에서 보다 일반적인 범용 커버 개념의 한 예로서, 범용 커버를 간단히 연결해야 한다는 위상학적 요건은 그래프-이론적 용어로 해석되어, 그것이 반복적이고 연결되어야 한다는 요건으로, 즉 나무로 해석된다.범용 피복 그래프는 독특하다(이형성까지).G가 나무라면 G 자체가 G의 보편적 커버 그래프인 것이다.다른 유한 연결 그래프 G의 경우 G의 범용 커버 그래프는 셀 수 없이 무한(그러나 국소적으로 유한) 나무다.

연결된 그래프 G의 범용 커버 그래프 T는 다음과 같이 구성할 수 있다.G의 임의 정점 r을 시작점으로 선택한다.T의 각 꼭지점은 R, 즉 G의 정점 w = (r, v1, v2, ..., vn)에서 시작하는 비역추적 보행이다.

  • v와i v는i+1 모두 G에 인접해 있다. 즉 w는 walk이다.
  • vi-1 ≠ v fori+1 all i, 즉 w는 비역추적이다.

그 다음, 하나의 정점(r, v1, v2, ..., vn)이 정점(r, v1, v2, v, v)에n-1 인접한 경우 T의 두 정점이 인접한다.이형성까지, 출발점 r의 선택과 상관없이 동일한 트리 T가 생성된다.

표지 지도 f는 T의 꼭지점(r)을 G의 꼭지점 r에, T의 꼭지점1(r2, v, vn, ..., v)을n G의 꼭지점 v에 매핑한다.

범용 커버의 예

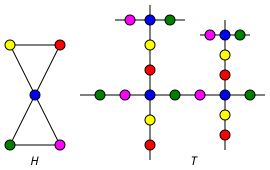
다음 그림은 그래프 H의 범용 커버 그래프 T를 보여준다. 색상은 커버 맵을 나타낸다.

Covering-graph-5.svg

모든 k에 대해 모든 k-규칙 그래프는 무한 k-규칙 트리라는 동일한 범용 표지를 가지고 있다.

위상결정

유한(멀티)그래프의 무한 폴드 아벨리안 커버 그래프를 위상학적 결정이라고 하는데, 결정 구조의 추상화라고 한다.예를 들어, 그래프로서의 다이아몬드 크리스탈은 네 개의 엣지 쌍극자 그래프의 최대 아벨리안 커버 그래프다.이 관점은 "표준 실현"이라는 개념과 결합되어 (초광학) 결정의 체계적인 설계에 유용한 것으로 판명되었다.[1]

플라나르

주요기사 : 평면커버

그래프의 평면 표지는 그 자체가 평면 그래프인 유한 피복 그래프다.평면 덮개를 갖는 특성은 금지된 미성년자가 특징지을 수 있지만, 이 형태의 정확한 특성화는 여전히 알려져 있지 않다.투사 평면에 내장되어 있는 모든 그래프에는 투사 평면의 방향성 있는 이중 커버에서 나오는 평면 커버가 있다. 1988년, 세이야 나가미는 이것들이 평면 커버를 가진 유일한 그래프라고 추측했지만, 이것은 증명되지 않은 채로 남아 있다.[3]

전압 그래프

그래프를 덮는 일반적인 방법은 전압 그래프를 사용하는데, 여기서 주어진 그래프 G의 다트(즉, G의 비방향 에지에 해당하는 방향 에지 쌍)는 일부 그룹의 원소의 역쌍으로 라벨을 표시한다.전압 그래프의 파생된 그래프는 쌍(v,x)의 정점으로서 여기서 v는 G의 정점이고 x는 그룹 요소인 그룹 요소 y로 라벨을 붙인 v에서 w까지의 다트는 파생 그래프에서 (v,x)에서 (w,xy)까지의 에지에 해당한다.

범용 커버는 이러한 방식으로 그래프의 스패닝 트리의 가장자리가 그룹의 ID 요소에 의해 라벨이 표시되고, 나머지 각 쌍의 다트는 자유 그룹의 구별되는 생성 요소에 의해 라벨이 표시되는 전압 그래프의 파생된 그래프로 볼 수 있다.초당적 이중은 이러한 방식으로 순서 2 그룹의 0이 아닌 원소에 의해 각 다트가 라벨을 붙이는 전압 그래프의 파생 그래프로 볼 수 있다.

메모들

  1. ^ a b Sunada, Toshikazu (2012). "6 Topological Crystals". Topological Crystallography: With a View Towards Discrete Geometric Analysis. Springer. pp. 73–90. ISBN 978-4-431-54177-6.
  2. ^ 안글루인 1980
  3. ^ Hliněný, Petr (2010), "20 years of Negami's planar cover conjecture" (PDF), Graphs and Combinatorics, 26 (4): 525–536, CiteSeerX 10.1.1.605.4932, doi:10.1007/s00373-010-0934-9, MR 2669457.

참조