크로스 스퀘어 큐폴라
Crossed square cupola| 크로스 스퀘어 큐폴라 | |
|---|---|
 | |
| 유형 | 존슨 이소모르프 큐폴라 |
| 얼굴 | 삼각형 4개 1+4제곱 1 옥타그램 |
| 가장자리 | 20 |
| 정점 | 12 |
| 꼭지점 구성 | 4+4(3.4.8/3) 4(3/2.43) |
| 슐레플리 기호 | {4/3} t{4/3} |
| 대칭군 | C4v, [4], (*44) |
| 회전군 | C4, [4]+, (44) |
| 이중 다면체 | - |
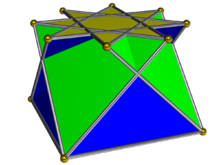
기하학에서 교차된 사각 큐폴라는 비콘벡스 존슨 고체 이소모르프 중 하나로, 지형학적으로 볼록한 사각 큐폴라와 동일하다.그것은 비콘벡스 대 롬비큐옥타헤드론 또는 콰시르옴비큐옥타헤드론의 한 조각으로 얻을 수 있다.모든 큐폴레에서와 같이, 기본 폴리곤은 상단보다 두 배 많은 에지와 정점을 가지고 있다. 이 경우 기본 폴리곤은 옥타그램이다.
정사각형 베이스가 역행하는 큐폴라라고 볼 수 있어 정사각형과 삼각형이 반대로 베이스를 가로질러 정사각형 큐폴라와 연결되어 서로 교차한다.
관련 다면체
| n/d | 4 | 5 | 7 | 8 |
|---|---|---|---|---|
| 3 |  {4/3} |  {5/3} |  {7/3} |  {8/3} |
| 5 | — | — |  {7/5} |  {8/5} |
교차된 사각 큐폴라는 어떤 균일한 다면체의 일부로 보일 수 있다.예를 들어, 대입방옥타헤드론은 삼각형 면에 연결된 6개의 교차 사각 큐폴레로 볼 수 있고, 비콘벡스 대합방 큐폴론은 6개의 큐폴레로 혼합된 것으로 볼 수 있다.또한, 비콘벡스 대 롬비큐옥타헤드론은 교차된 사각 큐폴레로 출토된 8진법을 가진 옥타그램 프리즘으로 볼 수 있는데, 이는 롬비큐옥타헤드론이 사각 큐폴레로 증강된 8진법을 가진 팔진 프리즘으로 볼 수 있는 방법과 유사하다.이 구조에서 큐폴레 중 하나를 회전시키면 사이비-위대 롬비쿠보톡타헤드론이 발생한다.여기에 비콘벡스 대 롬비헥사헤드론(nonconvx great rhombicuboctaheadron)을 구성하는 데 사용될 수 있는 이 세 가지 옥타그램 프리즘의 배타적 또는 모두로서 위대한 롬비헥사헤드론을 첨가할 수 있다.
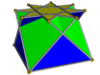 크로스 스퀘어 큐폴라 |  비콘벡스 대롬비쿠옥타헤드론 |  사이비-대단백옥타헤드론 |  대입방옥타헤드론 |  대록비헥사헤드론 |
아래 그림은 가로 사각 큐폴레가 한 번에 한 걸음씩 벌어지는 팔각형 프리즘의 발굴을 보여준다.교차된 사각 큐폴레는 항상 빨간색인 반면, 팔각형 프리즘의 사각형은 다른 색깔이다.모든 이미지는 명확성을 위해 거의 동일한 방식으로 방향이 지정된다.
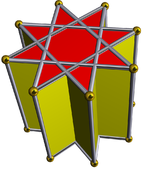 팔괘 프리즘(D8h 대칭으로 채색)은... | 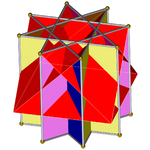 ... 교차된 사각 큐폴라와 함께 출토된 팔괘 중 하나(여기, 상단)로...이것은 역행 교차 사각 큐폴라 또는 증강 옥타그램 프리즘이라고 불릴 수 있으며, 존슨 길쭉한 사각 큐폴라에는 이형성이 있다. | 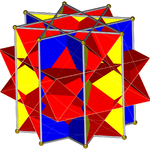 다른 크로스 스퀘어 큐폴라의 방향에는 두 가지 선택이 있다.하나는 해당 면(삼각형 삼각형, 사각형 사각형)을 정렬하고 비콘벡스 대 롬비옥타헤드론을 생성한다.이 구조는 D4h 대칭을 가지고 있지만, 비콘벡스 대칭은 완전한 팔면 대칭을 가지고 있다. | 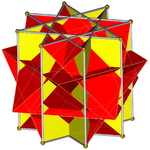 다른 선택은 반응하지 않는 얼굴(삼각형 사각형)을 정렬하고 사이비-대형 롬비큐브옥타헤드론(또는 사이비쿼시르옴비큐브옥타헤드론)을 생성한다.이4d 구조는 D 대칭이다. |
이러한 일련의 발굴은 팔각 프리즘의 해당 증축 시리즈와 쉽게 비교할 수 있다.
 팔각 프리즘(D8h 대칭으로 채색)은... | 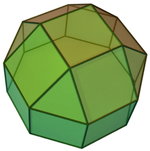 8각형 큐폴라로 증축한 옥타곤 중 하나로 |  다른 크로스 스퀘어 큐폴라의 방향에는 두 가지 선택이 있다.하나는 해당 면(삼각형 삼각형, 사각형 사각형)을 정렬하고 롬비큐옥타헤드론을 생성한다.Rhombicuboctaheadron은 완전한 팔면대칭을 가지고 있지만, 이4h 구조는 D 대칭을 가지고 있다. | 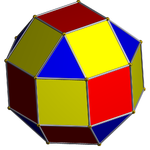 다른 선택은 반응하지 않는 얼굴(삼각형 사각형)을 정렬하고 유사롬비큐브옥타헤드론을 생성한다.이4d 구조는 D 대칭이다. |
이중 다면체
십자형 사각 큐폴라의 이중은 8개의 삼각형 면과 4개의 연면을 가지고 있다.
중앙 가까이 지나가는 교차 사각 큐폴라의 얼굴 때문에 이 이중은 외관이 매우 뾰족하다.이는 위대한 펜타키스 도데카헤드론(DU58)으로 알려진 이중 균일 다면체와 내부 역방향 오각형 육면체(DU60)에도 발생한다.
참조
- 짐 맥닐, 큐폴라 또는 세미쿠폴라
- Jim McNeill, Cupolas와 균일한 Polyedra의 관계



