크라운 그래프

크라운 그래프
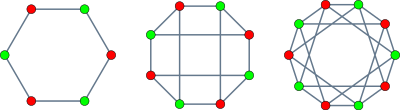정점이 6개, 8개 및 10개인 크라운 그래프
정점	2n
가장자리	n (n - 1)
반지름	${\displaystyle \left\{\put{n\leq 2\\\3&{\text}{nd{array}\right.}$
지름	${\displaystyle \left\{\put{n\leq 2\\\3&{\text}{nd{array}\right.}$
둘레	${\displaystyle \left\{\put{n\leq 2\\\6&n=3\\\n=\4&{\text}}\end{array}}\right}}$
색수	${\displaystyle \left\{\n1}{\put{array}{ll}n=1\\\2&{\text}{nd{array}}\right.}$
특성.	거리-변환
표기법	${\displaystyle S_{n}^{0}}}$
그래프 및 모수 표

수학의 한 분야인 그래프 이론에서, 2n 정점에 있는 크라운 그래프는 두 가지 정점 집합인 {u₁, u₂, ..., u_n}과(와₁) {v, v₂, v, ..., v_n}이(가) 있고, ≠ j가 있을 때마다 u에서_i v까지_j 에지가 있는 비방향 그래프다.

그 왕관 그래프에서 완벽한 일치의 가장자리를 제거하고 완전한 2부로 구성된 그래프로 완전한 그래프의 2부로 구성된 이중 덮개로 볼 수 있는 텐서 제품 Kn × K2는 보수의 데카르트 사상의 직접적인 제품의 Kn과 K2, 혹은 2부로 구성된 Kneser 그래프 Hn,1을 대표하는1-item과(n− 1)-item subse.의 이익n-message 집합(한 부분 집합이 다른 부분 집합에 포함될 때마다 두 부분 집합 사이에 가장자리가 있음)

예

6-Vertex 크라운 그래프는 주기를 형성하며, 8-Vertex 크라운 그래프는 큐브 그래프와 이형성이다.슐레플리 더블6에서는 12줄과 30개의 점을 3차원 공간에 배치한 12줄로 12볼텍스 크라운 그래프의 패턴으로 교차한다.

특성.

크라운 그래프의 가장자리 수는 발음 숫자 n(n - 1)이다.무채색 번호는 n: 각 쌍 {u, v_ii}을(를) 컬러 클래스 중 하나로 선택하여 완전한 색상을 찾을 수 있다.^[1]크라운 그래프는 대칭적이고 거리 변환적이다.아치디콘 외 (2004) 크라운 그래프의 가장자리 분할을 동일한 길이 사이클로 설명한다.

2n-Vertex 크라운 그래프를 4차원 유클리드 공간에 삽입하여 모든 가장자리의 단위 길이를 가질 수 있다.단, 이 임베딩은 또한 일부 비인접 정점들을 단위 거리만큼 떨어뜨릴 수 있다.가장자리가 단위 거리에 있고 비에지(non-edge)가 단위 거리에 있지 않은 내장에는 최소 n - 2차원이 필요하다.이 예는 그래프가 단위 거리 그래프와 엄격한 단위 거리 그래프로 표현되기 위해 매우 다른 치수를 요구할 수 있음을 보여준다.^[2]

크라운 그래프의 가장자리를 덮는 데 필요한 전체 초당적 하위 그래프의 최소 개수는 다음과 같다.

${\displaystyle \sigma(n)=\min \left\{\,k\mid n\leq}\binom {k}{\llfloor k/2\bloor }}\\right\}}}$

중심 이항 계수의 ^[3]역 함수

2n-Vertex 크라운 그래프의 보완 그래프는 완전 그래프₂ K $◻{\displaystyle }$ ${\displaystyle \square$}$K$_n 또는 동등하게 2 × n ruck's 그래프의 데카르트 제품이다.

적용들

예절상, 만찬에 손님을 배치하는 전통적 규칙은 남녀가 번갈아 가며 자리를 잡고, 부부끼리 서로 마주 앉는 일은 없어야 한다는 것이다.^[4]결혼하지 않은 부부들로 구성된 파티의 경우, 이 규칙을 만족하는 약정은 크라운 그래프의 해밀턴 사이클이라고 설명할 수 있다.예를 들어, 그림에 나타난 정점의 배치는 각 남편과 아내가 가능한 한 멀리 떨어져 앉아 있는 이런 유형의 좌석 차트로 해석될 수 있다.가능한 좌석 배치의 수, 또는 거의^[5] 동등하게 크라운 그래프의 해밀턴 사이클 수를 계산하는 문제는 콤비네이터학에서 메니지 문제로 알려져 있다; 6, 8, 10, ...정점을 이루는 크라운 그래프의 경우 해밀턴 사이클 수는 (지향적)이다.

2, 12, 312, 9600, 416880, 23879520, 1749363840, ...(OEIS의 경우 시퀀스 A094047)

크라운 그래프는 탐욕스러운 컬러링 알고리즘이 최악의 경우 나쁘게 작용한다는 것을 보여주는 데 사용될 수 있다: 크라운 그래프의 정점을 u₀, v₀, u₁, v 등의 순서로₁ 알고리즘에 제시하면 탐욕스러운 컬러는 n가지 색을 사용하는 반면 최적의 컬러 수는 두 가지다.이 구조는 존슨(1974)에 기인한다. 크라운 그래프는 존슨의 그래프라고 불리기도 한다. J_n.^[6] 퓨러(1995) 표기법은 색소 문제의 근사치의 경도를 보여주는 구성의 일부로 크라운 그래프를 사용한다.

마투셰크(1996)는 규범 벡터 공간에 내장하기 어려운 미터법 공간의 예로서 크라운 그래프의 거리를 사용한다.

미클라비치 & 포토치니크(2003)가 보여주듯이 크라운 그래프는 거리-정기 순환 그래프로서 발생할 수 있는 소수의 다른 유형의 그래프 중 하나이다.

Agarwal 외 연구진(1994)은 가시성 그래프로 크라운 그래프를 갖는 다각형을 설명하고, 가시성 그래프를 완전한 초당적 그래프의 조합으로 표현하는 것이 항상 공간 효율적이지 않을 수 있다는 것을 보여주기 위해 이 예를 사용한다.

정점이 2n인 크라운 그래프는 가장자리가 초당파의 한 쪽에서 다른 쪽으로 향하도록 하여 순서 차원 n으로 부분적으로 정렬된 집합의 표준 예를 형성한다.

메모들

참조

• Agarwal, Pankaj K.; Alon, Noga; Aronov, Boris; Suri, Subhash (1994), "Can visibility graphs be represented compactly?", Discrete and Computational Geometry, 12 (1): 347–365, doi:10.1007/BF02574385, MR 1298916.
• Archdeacon, D.; Debowsky, M.; Dinitz, J.; Gavlas, H. (2004), "Cycle systems in the complete bipartite graph minus a one-factor", Discrete Mathematics, 284 (1–3): 37–43, doi:10.1016/j.disc.2003.11.021, MR 2071894.
• Chaudhary, Amitabh; Vishwanathan, Sundar (2001), "Approximation algorithms for the achromatic number", Journal of Algorithms, 41 (2): 404–416, CiteSeerX 10.1.1.1.5562, doi:10.1006/jagm.2001.1192, MR 1869259.
• de Caen, Dominique; Gregory, David A.; Pullman, Norman J. (1981), "The Boolean rank of zero-one matrices", in Cadogan, Charles C. (ed.), Proc. 3rd Caribbean Conference on Combinatorics and Computing, Department of Mathematics, University of the West Indies, pp. 169–173, MR 0657202.
• Erdős, Paul; Simonovits, Miklós (1980), "On the chromatic number of geometric graphs" (PDF), Ars Combinatoria, 9: 229–246, MR 0582295.
• Fürer, Martin (1995), "Improved hardness results for approximating the chromatic number", Proc. 36th IEEE Symp. Foundations of Computer Science (FOCS '95), pp. 414–421, doi:10.1109/SFCS.1995.492572, ISBN 978-0-8186-7183-8.
• Johnson, D. S. (1974), "Worst-case behavior of graph coloring algorithms", Proc. 5th Southeastern Conf. on Combinatorics, Graph Theory, and Computing, Utilitas Mathematicae, Winnipeg, pp. 513–527, MR 0389644
• Kubale, M. (2004), Graph Colorings, American Mathematical Society, ISBN 978-0-8218-3458-9, MR 2074481
• Matoušek, Jiří (1996), "On the distortion required for embedding finite metric spaces into normed spaces", Israel Journal of Mathematics, 93 (1): 333–344, doi:10.1007/BF02761110, MR 1380650.
• Miklavič, Štefko; Potočnik, Primož (2003), "Distance-regular circulants", European Journal of Combinatorics, 24 (7): 777–784, doi:10.1016/S0195-6698(03)00117-3, MR 2009391.

외부 링크

• Weisstein, Eric W. "Crown Graph". MathWorld.