방향(기하학)
Orientation (geometry)기하학에서, 선, 평면, 강체와 같은 물체의 방향, 각도 위치, 자세 또는 방향은 그것이 [1]차지하는 공간에 어떻게 배치되는지에 대한 설명의 일부이다.구체적으로는 객체를 기준 배치에서 현재 배치로 이동하는 데 필요한 가상 회전을 나타냅니다.회전이 현재 위치에 도달하기에 충분하지 않을 수 있습니다.개체의 위치(또는 위치 또는 선형 위치)라고 하는 가상 변환을 추가해야 할 수 있습니다.위치와 방향은 물체가 어떻게 공간에 배치되는지를 완전히 설명합니다.상술한 상상의 회전과 변환은 물체의 방향은 번역할 때 변하지 않고 회전할 때 그 위치가 변하지 않기 때문에 어떤 순서로든 일어난다고 생각할 수 있다.
오일러의 회전 정리는 3차원에서 고정된 축을 중심으로 한 번의 회전으로 어떤 방향에도 도달할 수 있다는 것을 보여준다.이를 통해 축-각도 표현을 사용하여 방향을 표현하는 한 가지 일반적인 방법을 얻을 수 있습니다.다른 널리 사용되는 방법으로는 회전 사수, 회전자, 오일러 각도 또는 회전 행렬이 있습니다.보다 전문적인 용도에는 결정학, 지질학에서의 타격과 침하, 지도와 표지판의 등급이 포함됩니다.단위 벡터는 물체의 법선 벡터 방향 또는 두 점 사이의 상대 방향을 나타내기 위해 사용될 수도 있습니다.
일반적으로 방향은 기준 프레임을 기준으로 지정되며, 일반적으로 데카르트 좌표계에 의해 지정됩니다.
수학적 표현
3차원
일반적으로 강체 공간에서의 위치 및 방향은 주 기준 프레임에 대한 위치 및 방향으로 정의되며, 주 기준 프레임에 대해 고정되며, 따라서 주 기준 프레임과 함께 변환 및 회전합니다(차체의 국소 기준 프레임 또는 국소 좌표계).이 로컬 프레임의 방향을 기술하려면 적어도 3개의 독립된 값이 필요합니다.다른 세 가지 값은 객체의 점 위치를 나타냅니다.회전 축에 놓여 있는 점을 제외하고, 모든 차체 지점은 회전 중에 위치가 변경됩니다.강체가 회전 대칭인 경우 알려진 시작 방향에서 시간이 지남에 따라 방향이 어떻게 진화하는지를 관찰하는 경우를 제외하고 모든 방향을 구별할 수 있는 것은 아닙니다.예를 들어 선, 선분 또는 벡터 공간의 방향은 두 개의 값(예: 두 방향 코사인)만으로 지정할 수 있습니다.또 다른 예는 지구상의 점의 위치이며, 종종 지구의 중심과 연결되는 선의 방향을 사용하여 설명되며, 경도와 위도의 두 각도를 사용하여 측정됩니다.마찬가지로 평면의 방향도 예를 들어 평면에 수직인 선의 방향을 지정하거나 타격 및 딥 각도를 사용하여 두 가지 값으로 설명할 수 있습니다.
강체와 평면의 방향을 3차원으로 나타내기 위한 수학적 방법에 대한 자세한 내용은 다음 절에서 설명합니다.
2차원
2차원에서 객체(선, 벡터 또는 평면도형)의 방향은 단일 값, 즉 회전한 각도로 지정됩니다.자유도는 1개뿐이고 회전이 일어나는 고정점은 1개뿐입니다.
입체적인 강체
강체의 방향을 3차원으로 설명하는 몇 가지 방법이 개발되었습니다.다음 섹션에 요약되어 있습니다.
오일러 각도
방향을 나타내는 첫 번째 시도는 레온하르트 오일러에 기인한다.그는 서로 회전할 수 있는 세 개의 기준 프레임을 상상했고 고정된 기준 프레임에서 시작하여 세 번의 회전을 수행함으로써 공간에 있는 다른 기준 프레임을 얻을 수 있다는 것을 깨달았습니다(수직 축을 고정하기 위해 두 개의 회전을 사용하고 다른 두 개의 축을 고정하기 위해 다른 기준 프레임을 사용).이 세 회전의 값을 오일러 각도라고 합니다.
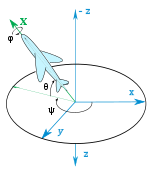
타이트-브라이언 각도
요, 피치 및 롤, 내비게이션 각도 및 카단 각도라고도 하는 세 가지 각도가 있습니다.수학적으로 그것들은 오일러 각도의 12가지 가능한 집합 안에 여섯 가지 가능성 집합을 구성하며, 그 순서는 비행기와 같은 차량의 방향을 설명하는 데 가장 잘 사용됩니다.항공우주공학에서 그것들은 보통 오일러 각도라고 불린다.
방향 벡터
오일러는 또한 두 회전의 구성이 다른 고정 축에 대한 단일 회전과 같다는 것을 깨달았다.따라서, 앞의 세 각도의 구성은 행렬이 개발될 때까지 계산하기 복잡한 축을 가진 하나의 회전과 같아야 한다.
이 사실을 바탕으로 그는 회전축 위의 벡터와 각도의 값과 동일한 모듈을 가진 모든 회전을 설명하는 벡터 방식을 도입했다.따라서 모든 방향은 기준 프레임에서 시작하는 회전 벡터(오일러 벡터라고도 함)로 나타낼 수 있습니다.방향을 나타내는 데 사용되는 회전 벡터는 일반적으로 방향 벡터 또는 자세 벡터라고 불립니다.
축 각도 표현이라고 하는 유사한 방법은 회전 축에 정렬된 단위 벡터와 각도를 나타내는 별도의 값을 사용하여 회전 또는 방향을 나타냅니다(그림 참조).
방향 매트릭스
행렬의 도입과 함께, 오일러 정리는 다시 쓰여졌다.회전 행렬은 회전 행렬 또는 방향 코사인 행렬이라고 하는 직교 행렬로 설명되었습니다.방향을 나타내는 데 사용되는 회전 행렬을 일반적으로 방향 행렬 또는 자세 행렬이라고 합니다.
위에서 언급한 오일러 벡터는 회전 행렬의 고유 벡터입니다(회전 행렬은 고유한 실제 고유 값을 가집니다).두 회전 행렬의 곱은 회전의 구성입니다.따라서 이전과 마찬가지로 초기 프레임에서 회전으로 방향을 지정해 설명하고자 하는 프레임을 달성할 수 있습니다.
n차원 공간에서 비대칭 물체의 구성 공간은 SO(n) × R이다n. 방향은 물체에 접선 벡터의 기초를 부착하여 시각화할 수 있다.각 벡터가 그 방향을 결정하는 방향.
오리엔테이션 4분위
회전을 설명하는 또 다른 방법은 베르사르라고도 하는 회전 사분위수를 사용하는 것입니다.회전 행렬 및 회전 벡터에 해당합니다.회전 벡터에 관해서는 행렬로 쉽게 변환할 수 있습니다.방향을 나타내기 위해 사용되는 회전 사분위는 일반적으로 방향 사분위 또는 자세 사분위라고 불립니다.
3차원 평면
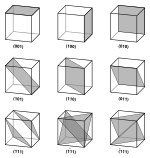
밀러 지수
격자 평면의 자세는 [2]평면에 수직인 선의 방향이며 평면의 밀러 지수로 설명됩니다.3공간에서 평면 패밀리(일련의 평행 평면)는 밀러 지수(hkl)[3][4]로 나타낼 수 있으므로 평면 패밀리는 모든 구성 평면에 공통의 자세를 갖는다.
스트라이크 앤 딥
지질학에서 관찰되는 많은 특징들은 평면이나 선이며, 그들의 방향은 일반적으로 그들의 태도라고 불린다.이러한 태도는 두 가지 각도로 명시됩니다.
선의 경우 이러한 각도를 추세 및 급락이라고 합니다.트렌드는 선의 나침반 방향이고, 급락은 수평면에서 [5]만드는 하향 각도입니다.
평면의 경우 두 각도를 타격(각도)과 딥(각도)이라고 합니다.스트라이크 라인은 수평 평면과 관측된 평면 형상(따라서 수평 선)의 교차점이며, 스트라이크 각도는 이 선의 방위(즉, 지리적 북쪽 또는 자기 북쪽을 기준으로 함)입니다.딥은 스트라이크 라인에 수직인 세 번째 수직면에서 관찰된 수평면과 관찰된 평면 형상 사이의 각도이다.
사용 예
강체
강체의 자세는 예를 들어 고정된 기준 프레임에 대한 차체 고정 프레임의 방향과 같이 설명되는 방향입니다.자세는 자세 좌표로 설명되며 최소 3개의 [6]좌표로 구성됩니다.강체의 방향을 결정하는 한 가지 방법은 체축 회전에 기초한다; 체축 고정 기준 프레임의 축을 중심으로 연속 세 번 회전하여 체체의 오일러 [7][8]각도를 설정한다.또 다른 용어는 롤, 피치 [9]및 요를 기준으로 하지만, 이러한 용어는 공칭 자세로부터의 증분 편차를 의미하기도 합니다.
「 」를 참조해 주세요.
레퍼런스
- ^ Robert J. Twiss; Eldridge M. Moores (1992). "§2.1 The orientation of structures". Structural Geology (2nd ed.). Macmillan. p. 11. ISBN 0-7167-2252-6.
...the attitude of a plane or a line — that is, its orientation in space — is fundamental to the description of structures.
- ^ William Anthony Granville (1904). "§178 Normal line to a surface". Elements of the Differential and Integral Calculus. Ginn & Company. p. 275.
- ^ Augustus Edward Hough Love (1892). A Treatise on the Mathematical Theory of Elasticity. Vol. 1. Cambridge University Press. p. 79 ff.
- ^ Marcus Frederick Charles Ladd; Rex Alfred Palmer (2003). "§2.3 Families of planes and interplanar spacings". Structure Determination by X-Ray Crystallography (4th ed.). Springer. p. 62 ff. ISBN 0-306-47454-9.
- ^ Stephen Mark Rowland; Ernest M. Duebendorfer; Ilsa M. Schiefelbein (2007). "Attitudes of lines and planes". Structural Analysis and Synthesis: A Laboratory Course in Structural Geology (3rd ed.). Wiley-Blackwell. p. 1 ff. ISBN 978-1-4051-1652-7.
- ^ Hanspeter Schaub; John L. Junkins (2003). "Rigid body kinematics". Analytical Mechanics of Space Systems. American Institute of Aeronautics and Astronautics. p. 71. ISBN 1-56347-563-4.
- ^ Jack B. Kuipers (2002). "Figure 4.7: Aircraft Euler angle sequence". Quaternions and Rotation Sequences: A Primer with Applications to Orbits, Aerospace, and Virtual Reality. Princeton University Press. p. 85. ISBN 0-691-10298-8.
- ^ Bong Wie (1998). "§5.2 Euler angles". Space Vehicle Dynamics and Control. American Institute of Aeronautics and Astronautics. p. 310. ISBN 1-56347-261-9.
Euler angle rigid body attitude.
- ^ Lorenzo Sciavicco; Bruno Siciliano (2000). "§2.4.2 Roll–pitch–yaw angles". Modelling and Control of Robot Manipulators (2nd ed.). Springer. p. 32. ISBN 1-85233-221-2.
외부 링크
 Wikimedia Commons의 오리엔테이션(수학) 관련 미디어
Wikimedia Commons의 오리엔테이션(수학) 관련 미디어