동적광 산란

DLS(Dynamic Light Disclanization, DLS)는 용액에 있는 중합체나 서스펜션의 작은 입자의 크기 분포 프로파일을 결정하는 데 사용할 수 있는 물리학의 기법이다.^[1] DLS의 범위에서 시간적 변동은 보통 강도나 광자 자동 상관 함수(광자 상관 분광 또는 준탄성 광 산란이라고도 한다)를 이용하여 분석한다. 시간영역 분석에서 자기 상관 함수(ACF)는 보통 지연 시간 0시부터 소멸하며, 작은 입자로 인한 역학 속도가 빨라 산란 강도 추적을 더 빨리 장식하게 된다. 강도 ACF는 전력 스펙트럼의 푸리에 변환이며, 따라서 DLS 측정은 스펙트럼 영역에서 동등하게 잘 수행될 수 있다.^[2][3] DLS는 또한 농축 고분자 용액과 같은 복잡한 액체의 작용을 조사하는 데 사용될 수 있다.

세우다

단색 광원, 보통 레이저가 편광기를 통과하여 샘플로 발사된다. 산란된 빛은 두 번째 편광기를 통과하여 광전자 증배기에 의해 수집되고 결과 영상이 화면에 투영된다. 이것을 반점무늬라고 한다(그림 1).^[4]

용액의 모든 분자는 빛으로 맞으며 모든 분자는 모든 방향으로 빛을 분산시킨다. 모든 분자로부터의 확산된 빛은 건설적으로(빛나는 지역) 간섭하거나 파괴적으로(어두운 지역) 간섭할 수 있다. 이 과정은 짧은 시간 간격으로 반복되며 그 결과 발생하는 얼룩무늬 세트는 시간 경과에 따른 각 지점의 빛의 세기를 비교하는 자기 상관자에 의해 분석된다. 편광기는 두 가지 기하학적 구성으로 설정할 수 있다. 하나는 수직/수직(VV) 지오메트리로, 두 번째 편광기가 빛을 통과하도록 하는 1차 편광기와 같은 방향이다. 수직/수평(VH) 기하학에서 두 번째 편광기는 입사광과 같은 방향이 아닌 빛을 허용한다.

설명

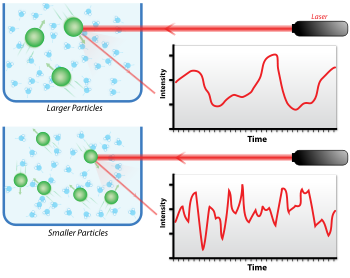
빛이 작은 입자에 닿으면 입자가 파장(250nm 이하)에 비해 작으면 빛이 사방으로 흩어진다(레이리 산란). 광원이 레이저라 단색적이고 일관성이 있다고 해도 산란 강도는 시간이 흐르면서 변동한다. 이러한 변동은 브라운 운동을 하는 서스펜션의 작은 입자에 기인하며, 따라서 용액의 산란자 사이의 거리는 시간에 따라 끊임없이 변화하고 있다. 이 산란된 빛은 그 후 주변 입자에 의해 건설적이거나 파괴적인 간섭을 겪게 되며, 이 강도 변동 내에는 산란자의 이동 시간 척도에 관한 정보가 포함되어 있다. 여과나 원심분리를 통한 검체 준비는 용액에서 먼지와 유물을 제거하는데 매우 중요하다.

입자의 동적 정보는 실험 중에 기록된 강도 추적의 자기 상관에서 도출된다. 두 번째 순서 자기 상관 곡선은 다음과 같이 강도 추적에서 생성된다.

${\displaystyle g^{2}(q;\tau )={\frac {\langle I(t)I(t+\tau )\angle }{\langle I(t)\angle ^{2}}:$

여기서 (;)qτ는 특정 파형 벡터, , 및 지연 시간에서의 자기 상관 함수로서 강도 입니다. 각괄호 <>는 기대치 연산자를 나타내며, 일부 텍스트에서는 자본으로 표시된다.

짧은 시간 지연 시, 입자가 있었던 초기 상태로부터 크게 움직일 기회가 없기 때문에 상관관계가 높다. 따라서 두 신호는 매우 짧은 시간 간격 후에 비교했을 때 본질적으로 변하지 않는다. 시간 지연이 길어질수록 상관관계는 기하급수적으로 감소하며, 이는 오랜 시간이 경과한 후 초기 상태와 최종 상태의 산란 강도 사이에는 상관관계가 없다는 것을 의미한다. 이 기하급수적인 붕괴는 입자의 운동, 특히 확산계수와 관련이 있다. 붕괴(즉 자기 상관 함수)를 맞추기 위해 가정된 분포의 계산에 기초하여 수치적 방법을 사용한다. 만약 표본이 단수체(균일)라면, 붕괴는 단지 하나의 지수일 뿐이다. Siegert 방정식은 2차 자기 상관 함수와 1차 자기 상관 함수(;)qτ를 다음과 같이 연관시킨다.

${\displaystyle g^{2}(q;\tau )=1+\properties \left[g^{1}(q;\tau )\right]^{2}}$

여기서 매개변수는 광 산란 설정에서 레이저 빔의 형상 및 정렬에 따라 달라지는 보정 계수다. 빛이 모이는 반점수(반점무늬 참조)의 반비례와 대략 같다. 레이저 빔의 작은 초점은 응고자 반점 패턴, 검출기에 작은 반점 수를 나타내며, 따라서 2차 자기 상관 순서가 더 크다.

자기 상관 함수의 가장 중요한 사용은 크기 결정에 사용하는 것이다.

다중 산란

동적 광 산란(dynamic light screaming)은 단일 산란 이벤트를 측정하여 부드러운 물질의 동적 특성에 대한 통찰력을 제공하는데, 이는 각 검출된 광자가 표본에 의해 정확히 한 번 산란되었음을 의미한다. 그러나 과학적이고 산업적인 관련성이 있는 많은 시스템에 대한 적용은 종종 계산된 다중 산란으로 인해 제한되어 왔으며, 광자는 검체에 의해 여러 번 산란된 후 검출되었다. 다중 산란으로 인한 비적합성 기여도가 있는 시스템의 경우 정확한 해석은 매우 어려워진다. 특히 더 큰 입자와 굴절률 대조가 높은 입자의 경우, 이것은 기법을 매우 낮은 입자 농도로 제한하며, 따라서 다양한 시스템은 동적 빛의 산란과 함께 조사에서 제외된다. 그러나 샤에첼이 보여주듯이 교차상관 접근법을 통해 동적 광 산란 실험에서 다중 산란을 억제할 수 있다.^[5] 일반적인 생각은 동적 광 산란 실험에서 개별적으로 산란된 빛을 분리하고 원치 않는 기여를 다중 산란으로부터 억제하는 것이다. 상이한 교차 상관 광 산란 구현이 개발되어 적용되었다. 현재 가장 널리 사용되는 방식은 이른바 3D 동적 광 산란법이다.^[6][7] 다중 산란 기여도에 대한 정적 광 산란 데이터를 수정하는 데도 동일한 방법을 사용할 수 있다.^[8] 또는 강한 다중 산란 한계에서는 확산파 분광법이라는 동적 광 산란 변종을 적용할 수 있다.

데이터 분석

소개

일단 자기 상관 데이터가 생성되면, 그것으로부터 '정보'를 결정하기 위해 다른 수학적 접근법을 사용할 수 있다. 산란 분석은 입자가 이온 사이의 충돌이나 정전력을 통해 상호작용하지 않을 때 촉진된다. 입자-입자 충돌은 희석하여 억제할 수 있으며, 전기적 이중층을 붕괴시키기 위해 소금을 사용함으로써 전하 효과가 감소한다.

가장 간단한 방법은 첫 번째 순서 자기 상관 함수를 단일 지수 붕괴로 처리하는 것이다. 이것은 모노디세르드 인구에 적합하다.

${\displaystyle \g^{1}(q;\tau )=\exp(-\Gamma \tau )\,}$

여기서 γ은 붕괴율이다. 변환 확산 계수는 파형 벡터에 따라 단일 각도 또는 각도 범위에서 도출될 수 있다.

${\displaystyle \\Gamma =q^{2}D_{t}\,}$

와 함께

${\displaystyle \q={\frac {4\pi n_{0}}{\pida }}}}\sin \leftda }\preck {\theta }{2}}\오른쪽)}$

여기서 λ은 입사 레이저 파장이며, 샘플의 굴절률이며, 샘플 셀과 관련하여 검출기가 위치한 각도다.

시스템의 음이소트로피와 다분산성에 따라 (AND/)q² 대 결과 그림의 각의존도가 나타날 수도 있고 그렇지 않을 수도 있다. 작은 구형 입자는 각도에 의존하지 않기 때문에 음이소트로피가 없다. (γ/)q² 대(-)의 플롯은 수평선이 된다. 구가 아닌 형상을 가진 입자는 음이소트로피(anisotropy)를 나타내며, 따라서 ( vs/)q² 대. 어떤 경우에도 절편은 D가_t 될 것이다.^[9] 따라서 각 입자 크기에 대한 최적의 검출 각도가 있다. 고품질 분석은 항상 여러 산란 각도(다각 DLS)에서 수행해야 한다. 이것은 알 수 없는 입자 크기 분포를 가진 다면체 표본에서 훨씬 더 중요해진다. 특정 각도에서 일부 입자의 산란 강도는 다른 입자의 약한 산란 신호를 완전히 압도하여 이 각도에서 데이터 분석에는 보이지 않게 한다. 일정한 각도에서만 작동하는 DLS 기기는 일부 입자에게만 좋은 결과를 제공할 수 있다. 따라서 검출 각도가 하나만 있는 DLS 기기의 표시된 정밀도는 특정 입자에 대해서만 적용된다.

D_t 스톡스-아인슈타인 방정식을 통해 구의 유체역동반경을 계산하는 데 종종 사용된다. 동적 빛의 산란으로 결정되는 크기는 산란기와 같은 방식으로 움직이는 구의 크기라는 점에 유의해야 한다. 따라서 예를 들어 산란기가 무작위 코일 폴리머인 경우 결정된 크기는 정적 광 산란으로 결정되는 규율 반지름과 같지 않다. 또한 얻어진 크기가 입자와 함께 움직이는 다른 분자나 용매 분자를 포함할 것이라는 점을 지적하는 것도 유용하다. 그래서 예를 들어 계면활성제 층을 가진 콜로이드 금은 전송 전자현미경 검사(대조도가 나빠 층을 "보기"하지 않음)보다 동적 빛의 산란(계면활성제 층 포함)에 의해 더 크게 나타날 것이다.

대부분의 경우, 표본은 다산염이다. 따라서 자기 상관 함수는 모집단의 각 종에 해당하는 지수 해독의 합이다.

${\displaystyle g^{1}(q;\tau )=\sum _{i=1}^{n_{i}(\Gamma_-\Gamma_{i}\tau )=\int G(\Gamma \tau )\exp(-\\\\\\Gama.}$

(;)qτ에 대한 데이터를 얻고 위 내용을 뒤집어서 (vert)를 추출하려고 시도하면 유혹적이다. (Ⅱ)는 각 종에서 발생하는 상대적 산란과 비례하기 때문에 크기 분포에 관한 정보를 담고 있다. 그러나 이것은 잘못된 문제로 알려져 있다. 아래에 기술된 방법(및 기타)은 자기 상관 함수에서 가능한 많은 유용한 정보를 추출하기 위해 개발되었다.

적분법

가장 일반적인 방법 중 하나는 누적된 방법인데,^[10][11] 이 방법에서 위의 지수들의 합계에 더하여 다음과 같이 시스템의 분산에 대한 더 많은 정보를 얻을 수 있다.

${\displaystyle \g^{1}(q;\tau )=\exp \left(-{\bar {\Gamma }}}}\flau -{\frac {\mu_{2}}!}}}\tau ^{2}+{\frac {\mu _{3}}{3}}{3!}}}\tau ^{3}+\cdots \오른쪽)}$

여기서 γ은 평균 붕괴율이고 /γ은² 두 번째 순서의 다분산 지수(또는 분산의 표시)이다. 3차 다분산 지수도 도출할 수 있지만 이는 시스템의 입자가 고다분산인 경우에만 필요하다. z-평균 변환 확산 계수는 파형 벡터 q에 따라 단일 각도 또는 각도 범위에서 도출될 수 있다.

${\displaystyle \\bar {\\\Gamma }}=q^{2}D_{z}\,}$

적산법은 작고 충분히 좁은()에 유효하다는 점을 유념해야 한다.Γ^[12] 파워 시리즈 확장에 많은 파라미터를 사용하여 데이터를 오버핏하면 $\gamma$의${\$ 및$$ µs를₂ 포함한 모든 파라미터를 덜 정밀하게 렌더링하기 때문에 µ₃ 이상의 파라미터를 사용하면 안 된다.^[13] 누적 방법은 아래 방법보다 실험 소음의 영향을 훨씬 덜 받는다.

CONTENT 알고리즘

자기 상관 함수를 분석하는 대체 방법은 스티븐 프로벤처가 개발한 CONTENTER라고 알려진 역 라플라스 변환을 통해 얻을 수 있다.^[14][15] CONTENT 분석은 적분법으로 해결할 수 없는 이질화, 폴리분해 및 멀티모달 시스템에 이상적이다. 두 개의 서로 다른 입자 집단을 분리하기 위한 분해능은 대략 5개 이상의 요인이고 두 개의 다른 모집단 사이의 상대 강도 차이는 1:10⁻⁵ 미만이어야 한다.

최대 엔트로피법

최대 엔트로피(Maximum Entropy) 방법은 발전 가능성이 큰 분석 방법이다. 이 방법은 또한 분석초음파에서 발생하는 침전 속도 데이터의 정량화에도 사용된다. 최대 엔트로피 방법은 실험 데이터에서 적합 데이터의 편차를 최소화하고 그에 따라 적합 데이터의 χ을² 줄이기 위한 여러 반복 단계를 포함한다.

비구형 입자의 산란

만약 문제의 입자가 구형이 아니라면 빛의 산란도 방향에 따라 달라지기 때문에 회전 운동도 고려해야 한다. Pecora에 따르면, 입자가 두 가지 조건을 충족시킬 때 회전 브라운 운동은 산란에 영향을 줄 것이다; 그것들은 광학적으로나 기하학적으로 비등방성이어야 한다.^[16] 로드형 분자는 이러한 요건을 충족하므로 변환 확산 계수 외에 회전 확산 계수를 고려해야 한다. 그것의 가장 간결한 형태에서 방정식은 다음과 같이 나타난다.

${\displaystyle {\frac {A}{B}}={\frac {5}{4}}{\frac {4\mathrm {M} _{p}+2\mathrm {N} \mathrm {M} _{l}\mathrm {M} _{p}+\mathrm {M} _{l}}{\mathrm {M} _{p}-\mathrm {N} +\mathrm {M} _{l}}}}$

여기서 B/는 두 이완 모드(변환 및 회전)의 비율이며, M은_p 입자의 중심축에 수직인 축에 대한 정보를 포함하고, M은_l 중심축과 평행한 축에 대한 정보를 포함한다.

2007년에 피터 R. 랭과 그의 팀은 짧은 금 나노로드의 입자 길이와 가로 세로 비율을 결정하기 위해 동적 빛의 산란을 사용하기로 결정했다.^[17] 샘플을 파괴하지 않고 상대적으로 설정이 쉽다는 이유로 이 방식을 택한 것이다. 두 이완 상태는 모두 VV 기하학에서 관찰되었으며, 두 동작의 확산 계수를 사용하여 금 나노입자의 가로 세로 비율을 계산하였다.

적용들

DLS는 단백질, 중합체, 마이크로셀, 베실체, 탄수화물, 나노입자,^[18] 생물세포^[19], 젤 등 다양한 입자의 크기를 특성화하는 데 사용된다.^[20] 시스템이 크기가 분산되지 않으면 입자의 평균 유효 직경을 결정할 수 있다. 이 측정은 입자 코어의 크기, 표면 구조물의 크기, 입자 농도, 매질의 이온 종류에 따라 달라진다.

DLS는 기본적으로 입자 확산으로 인한 산란 광도의 변동을 측정하기 때문에 입자의 확산 계수를 파악할 수 있다. 상용 계측기의 DLS 소프트웨어는 일반적으로 입자 모집단을 다른 직경으로 표시한다. 만약 시스템이 단색체라면, 다색체계는 여러 개의 입자 집단을 보여주는 반면, 한 개의 모집단만 있어야 한다. 표본에 둘 이상의 크기 모집단이 있는 경우 광자 상관 분광기기에 CONTERNATION 분석을 적용하거나 도플러 시프트 계측기에 파워 스펙트럼 방법을 적용해야 한다.

안정성 연구는 DLS를 이용하여 편리하게 수행할 수 있다. 표본의 주기적 DLS 측정은 입자의 유체역학 반경이 증가하는지 여부를 확인함으로써 입자들이 시간에 따라 집합하는지를 보여줄 수 있다. 입자가 모이면 반지름이 더 큰 입자 집단이 더 많아진다. 일부 DLS 기계에서는 온도에 따른 안정성을 상황별 온도 조절을 통해 분석할 수 있다.

위키미디어 커먼즈에는 동적 빛의 산란과 관련된 미디어가 있다.

참고 항목

참조

외부 링크

• 용액에서 브라운 운동에서 작은 구슬의 반지름을 결정하는 DLS
• DLS를 사용한 입자 크기 조정
• 라이타이저
• 단백질, 중합체 및 콜로이드 분산의 입자 크기 특성화를 위한 동적 광 산란