등각 오각형

이 글은 검증을 위해 인용구가 추가로 필요하다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선할 수 있도록 도와주십시오. 공급되지 않은 재료는 도전하여 제거할 수 있다. 출처 찾기: "등각형 펜타곤" – 뉴스 · 신문 · 책 · 학자 · JSTOR (2014년 8월) (이 템플릿 메시지를 제거하는 방법과 시기 학습)

기하학에서 정삼각형은 유클리드 평면에서 길이가 같은 5개의 변을 가진 다각형이다.그것의 5개의 꼭지점 각도는 일련의 값들을 가질 수 있고, 따라서 그것은 5각형의 가족을 형성할 수 있다.이와는 대조적으로, 정규 오각형은 등각형이고 더욱이 등각형이기 때문에 독특하다. (5각은 등각이며, 측정치는 108도)

닫힌 체인으로 배열된 네 개의 교차하는 등원으로는 볼록한 등각 오각형을 결정하기에 충분하다.각 원의 중심은 오각형의 네 꼭지점 중 하나이다.나머지 꼭지점은 체인의 첫 번째 원과 마지막 원의 교차점 중 하나에 의해 결정된다.

예

정규 오각형 (196° 내부 각도)	인접 직각 (60°,150°,90°,90°,150°)	반사형 일반 펜타곤 (36°,252°,36°,108°,108°)	항성 펜타그램 (36°)	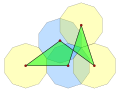교차 (36°,108°,−36°,−36°,108°)	사다리꼴로 퇴화하다. (가장자리 접기) (120°,120°,60°,0°,60°)
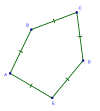볼록스		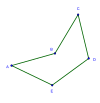오목한	자가 교차	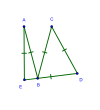퇴보하다 (에지-벡스 겹침)	삼각형으로 퇴화하다. (가장자리 접기) (≈28.07°,0°,≈75.96°,≈75.96°,0°)

볼록 등각형 오각형의 내부 각도

볼록한 등각형 오각형을 삼각형으로 해부하면 두 개가 이소체(주황색과 파란색의 삼각형)로 나타나는 반면 다른 하나는 더 일반적이다(녹색의 삼각형).우리는 우리에게 인접한 각도 $\alpha {\displaystyle }$ ${\displaystyle \alpha }$과 $\beta {\displaystyle }$ ${\displaystyle \beta }$이 주어진다고 가정한다$.$

시네스의 법칙에 따르면 녹색 삼각형과 파란색 삼각형을 나누는 선의 길이는 다음과 같다.

${\displaystyle a=2\sin \left\frac {}{2}}\오른쪽).}$

주황색 삼각형과 녹색 삼각형을 나누는 선의 길이의 제곱은 다음과 같다.

${\displaystyle {\begin{aligned}b^{2}&=1+a^{2}-2(1)(a)\cos \left(\alpha -{\frac {\pi }{2}}+{\frac {\beta }{2}}\right)\\&=1+4\sin ^{2}\left({\frac {\beta }{2}}\right)-4\sin \left({\frac {\beta }{2}}\right)\sin \left(\alpha +{\frac {\beta }{2}}\right).\\end{aigned}}$

코사인 법칙에 따르면 Δ의 코사인(cosine)은 다음과 같은 그림에서 볼 수 있다.

${\displaystyle \cos(\property )={\frac {1^{2}+1^{2}-b^{2}}:{2(1)(1)\ .}$

단순화, Δ는 α와 β의 함수로 구한다.

${\displaystyle \cos(\cos(\cos)(\cos)(\cos)(\cos)(\cos)(\cos)(\cos(\cos)(\cos)(\cos)(\cos)(\cos)(\cos)(\cos)(\cos)({1}{1}:{2}}\오른쪽).}$

오각형의 나머지 각도는 기하학적으로 찾을 수 있다.주황색과 파란색 삼각형의 나머지 각도는 이등변 삼각형의 두 각도가 동일한 반면 세 각도는 모두 180°에 해당한다는 것을 알아냄으로써 쉽게 찾을 수 있다.그러면 $ϵ{\displaystyle }$ ,${\displaystyle \gamma }$ ,$\$ , {\$displaystyle \epsilon$ ,\$gamma$ $,}$과 녹색 삼각형의 나머지 두 각도는 오각형의 합이 540°, 녹색 삼각형의 각도의 합이 180°, $각도$는 {$${\$displaystyle \gamma}$이며, 각도는 그$$ 세 성분의 합이라고 하는 4개의 방정식에서 찾을 수 있다.${\displaystyle ϵ}$ ${\displaystyle \epsilon }$은(는) 두 구성 요소의 합이다.

주기적인 오각형은 만약 그것이 동일한 면을 가지고 있고 따라서 규칙적인 경우에만 등각형이다.마찬가지로 접선 오각형은 만약 그것이 동일한 각도를 가지고 있고 따라서 규칙적인 경우에만 등각이다.^[1]

타일링

평면 타일을 이루는 2개의 무한대의 등각형 볼록 5각형이 있으며, 하나는 인접한 2개의 보완각과 다른 하나는 2개의 비인접 보완각이다.이 펜타곤들 중 일부는 한 가지 이상의 방법으로 타일을 칠할 수 있으며, 평면에는 타일을 칠할 수 있지만 이 두 계열 중 어느 한 계열에 속하지 않는 등방형 오각형의 산발적인 예가 있다. 각도는 89°16', 144°32'30', 70°55', 135°22' 및 99°54'30'30'이며, 상호보완적이지 않다.^[2]

2차원 매핑

등각형 펜타곤은 전혀, 한 번, 두 번 또는 다섯 번 서로 교차할 수 있다.스스로 교차하지 않는 것을 단순이라고 하며, 볼록하거나 오목한 것으로 분류할 수 있다.여기서 우리는 두 번 또는 다섯 번 서로 교차하는 것을 가리키기 위해 "stellated"라는 용어를 사용한다.우리는 이 절에서 정확히 한 번 교차하는 정삼각형 오각형을 배제한다.

한 번 자기들끼리 교차하는 오각형을 배제한다는 점에서 나머지는 2차원 평면에서 두 변수의 함수로 그려볼 수 있다.각 값 쌍(α, β)은 평면의 단일 지점에 매핑되며, 또한 단일 오각형에도 매핑된다.

α 및 β 값의 주기성과 조건 α β Δ는 매핑의 크기를 제한하도록 허용한다.좌표 축 α와 β가 있는 평면에서 방정식 α = β는 평면을 두 부분(도면의 주황색으로 표시된 남쪽 경계)으로 나누는 선이다.곡선으로 Δ = β라는 방정식은 평면을 다른 섹션으로 나눈다(파란색으로 표시된 북쪽 경계).

두 경계는 점들이 독특한 등변형 5각형에 매핑되는 평면의 연속 영역을 둘러싸고 있다.영역 밖의 지점은 반복된 펜타곤(회전하거나 반사되었을 때 이미 설명한 것과 일치할 수 있는 펜타곤)에 매핑된다.정확히 그 경계선에 지도를 그리는 펜타곤은 대칭선을 가지고 있다.

독특한 매핑의 영역 안에는 새로운 경계선으로 구분된 stellated, oomal, colfx의 세 가지 형태의 펜타곤이 있다.

스텔라티드

잘려진 오각형들은 다른 면들과 교차한다.이런 종류의 펜타곤의 일반적인 예는 펜타그램이다.펜타곤을 절개하거나 자가 절개하는 조건은 2α + β ≤ 180°이어야 한다.따라서 지도화에서 선 2α + β = 180°(북쪽에 주황색으로 표시됨)는 스테어링된 펜타곤과 비스텔링된 펜타곤 지역 사이의 경계선이다.이 국경에 정확히 지도하는 펜타곤은 정점이 다른 면에 닿는다.

오목한

오목한 오목한 오목한 오목한 오목한 오목한 오목한 오목한 오목한 오목한 오목한 오목한 오목한 오목한 오각은 적어도180°보다 넓게 열리는 첫 번째 각도는 γ이므로 방정식 γ = 180°(오른쪽에서 녹색으로 표시)는 오목한 펜타곤 등의 영역의 경계인 곡선으로 볼록이라고 한다.이 국경에 정확히 지도를 그리는 펜타곤은 적어도 두 개의 면이 연속해서 이중 길이 면으로 나타나는데, 이것은 사오각으로 퇴화된 오각형을 닮았다.

볼록스

볼록 펜타곤은 5개의 각도가 모두 180°보다 작으며 다른 각도와 교차하는 면이 없다.이런 유형의 오각형의 일반적인 예는 일반 오각형이다.

참조

위키미디어 커먼스는 에퀴엠티브 펜타곤과 관련된 미디어를 가지고 있다.