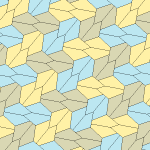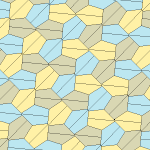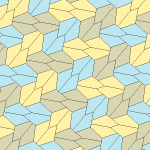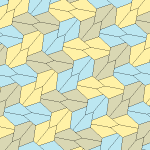
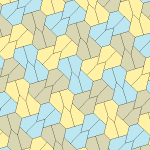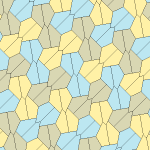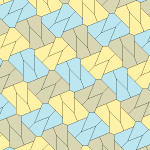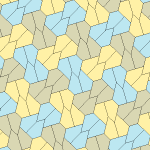
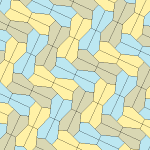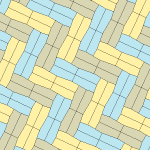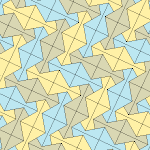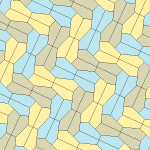
오각형 타일링
Pentagonal tiling
기하학에서 오각형 타일링은 각 조각이 오각형 모양으로 되어 있는 평면의 타일링이다.
유클리드 평면의 정기적인 오각형 타일링은 108°의 일반 오각형 내부 각도가 전체 턴의 각도인 360°의 디비저가 아니기 때문에 불가능하다. 그러나, 일반 펜타곤은 쌍곡면과 구를 타일로 만들 수 있다; 후자는 도데카헤드론에 해당하는 타일링을 위상학적으로 생산한다.[1]
모노헤드 볼록 오각 틸팅
15가지 종류의 볼록 펜타곤은 일면 타일로 알려져 있다([2]즉, 한 가지 유형의 타일로). 가장 최근의 것은 2015년에 발견되었다. 이 목록은 Rao (2017)에 의해 완결된 것으로 나타났다(결과적으로 동료 검토 대상). 바기나(2011년)는 엣지 대 엣지 볼록스 종류가 8종밖에 없다는 것을 보여주었는데, 스기모토(2012년)가 독자적으로 얻은 결과다.
에콜 노르말 수페리우레 드 리옹의 마이클 라오는 2017년 5월 이 15종 이상의 볼록 펜타곤이 실제로 없다는 증거를 발견했다고 주장했다.[3] 2017년 7월 11일 현재 라오 증명의 전반부는 토머스 헤일스 피츠버그대 수학과 교수가 독자적으로 검증(컴퓨터 코드 사용[4] 가능)한 상태였다.[5] 2017년 12월 현재, 그 증거는 아직 완전히 동료 검토가 되지 않았다.
열거된 각 타일링 패밀리는 다른 형식에 속하지 않는 펜타곤을 포함한다. 그러나, 일부 개별 펜타곤은 복수의 형식에 속할 수 있다. 또한 알려진 타일링 유형의 일부 펜타곤은 타일링 유형의 모든 구성원이 표시하는 표준 타일링 이상의 대체 타일링 패턴을 허용하기도 한다.
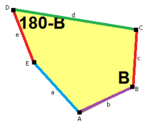
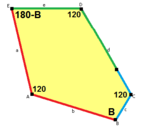
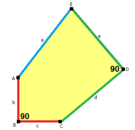
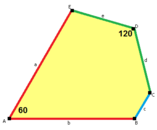
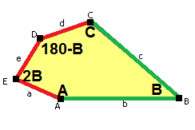
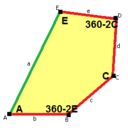
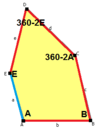
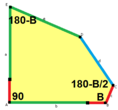
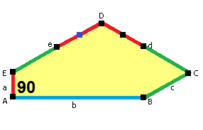
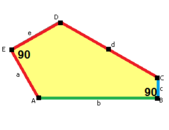
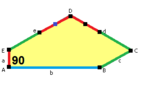
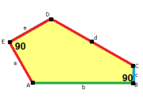
길이 a, b, c, d, e의 옆면은 각각 정점 A, B, C, D, E의 각도에서 시계방향으로 직각한다. (Thus, A, B, C, D, E는 각각 d, e, a, b, c와 반대방향이다.)
| 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|
 B + C = 180° A + D + E = 360° |  c = e B + D = 180° |  a = b, d = c + e A = C = D = 120° |  b = c, d = e B = D = 90° |  a = b, d = e A = 60°, D = 120° |
| 6 | 7 | 8 | 9 | 10 |
 a = d = e, b = c B + D = 180°, 2B = E |  b = c = d = e B + 2E = 2C + D = 360° |  b = c = d = e 2B + C = D + 2E = 360° |  b = c = d = e 2A + C = D + 2E = 360° |  a = b = c + e A = 90°, B + E = 180° B + 2C = 360° |
| 11 | 12 | 13 | 14 | 15 |
 2a + c = d = e A = 90°, C + E = 180° 2B + C = 360° |  2a = d = c + e A = 90°, C + E = 180° 2B + C = 360° |  d = 2a = 2e B = E = 90° 2A + D = 360° |  2a = 2c = d = e A = 90°, B ≈ 145.34°, C ≈ 69.32° D ≈ 124.66°, E ≈ 110.68° (2B + C = 360°, C + E = 180°) |  a = c = e, b = 2a A = 150°, B = 60°, C = 135° D = 105°, E = 90° |
이러한 단면 타일 유형의 대부분은 자유도를 가지고 있다. 이러한 자유는 내부 각도와 가장자리 길이의 변화를 포함한다. 한계에서 가장자리는 0에 접근하는 길이 또는 180°에 접근하는 각도를 가질 수 있다. 유형 1, 2, 4, 5, 6, 7, 8, 9 및 13은 비콘벡스 프로토타일과의 파라메트릭 가능성을 허용한다.
주기적인 기울기는 벽지 그룹 대칭으로 특징지어진다. 예를 들어, p2(222)는 4개의 2배 회전 지점으로 정의된다. 이 명칭은 아래 도표에 사용되며, 여기서 타일은 대칭 내의 k-면 위치에 의해 색상이 지정된다.
원시 단위는 타일링의 한 부분으로 번역만 사용하여 전체 타일링을 생성하는 것으로 가능한 한 작다.
라인하르트 (1918년)
라인하르트(1918)는 처음 다섯 종류의 오각형 타일을 발견했다. 다섯 개 모두 등면 기울기를 만들 수 있는데, 이는 타일링의 대칭이 어떤 타일을 다른 타일로 가져갈 수 있다는 것을 의미한다(더 공식적으로, 오토모피즘 그룹은 타일 위에서 트랜스적으로 작용한다).
B. 그룬바움과 G. C. 셰퍼드 교수는 5각형 기준면에 의한 평면 등면 기울기의 "형식"이 정확히 24개라는 것을 보여주었다.[6] 모두 일반적으로 타일링에 필요한 추가 조건을 갖춘 라인하르트의 타일을 사용한다. 2타입의 기와에는 모두 2개의 기울기가 있고, 나머지 4타입에는 모두 하나씩 있다. 나머지 18개 기울기 중 15개는 제1종 타일의 특수한 경우다. 24개 기울기 중 9개가 최첨단을 이루고 있다.[7]
또한 제1종, 제2종, 제4종 타일 특례에 의한 2면 기울기가 있고, 제1종 타일 특례에 의한 3면 기울기가 모두 있다. 유형 1과 유형 2인 특정 타일에 의한 k-면 기울기에 대한 상한은 없으므로 원시 단위의 타일 수에는 상한이 없다.
각 타일링에 대한 벽지 그룹 대칭은 괄호 안에 오비폴드 표기법과 함께 주어진다. 두 번째 하위 대칭 그룹은 기와 치레가 존재할 경우 주어지며, 여기서 거울 이미지는 구별되는 것으로 간주된다. 이 경우 노란색과 녹색 타일로 표시된다.
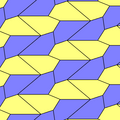
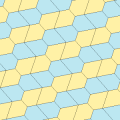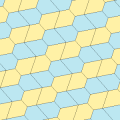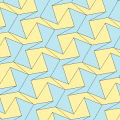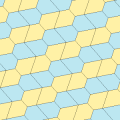
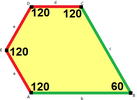
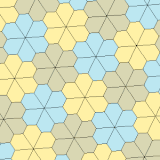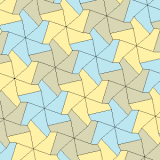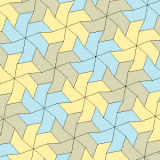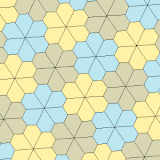
유형 1
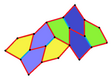
1형 펜타곤을 포함하는 타일링 토폴로지가 많다. 아래에는 다섯 가지 위상이 제시되어 있다.
| p2(222) | cmm(2*22) | cm(*×) | pmg(22*) | pgg(22×) | p2(222) | cmm(2*22) |
|---|---|---|---|---|---|---|
| p1 (°) | p2(222) | p2(222) | ||||
 |  |  |  |  |  |  |
| 2-162 원시 단위 | 4-162 원시 단위 | |||||
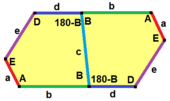 B + C = 180° A + D + E = 360° |  a = c, d = e A + B = 180° C + D + E = 360° | 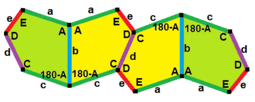 a = c A + B = 180° C + D + E = 360° | 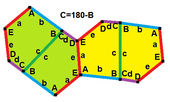 a = e B + C = 180° A + D + E = 360° |  d = c + e A = 90°, 2B + C = 360° C + D = 180° B + E = 270° | ||
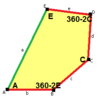
유형 2
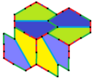
이 타입 2의 예는 등면이다. 두 번째는 에지 대 에지 변형이다. 그들은 둘 다 pgg(22×) 대칭을 가지고 있다. 미러 이미지 타일(노란색 및 녹색)이 구별되는 것으로 간주되는 경우 대칭은 p2(222)이다.
| pgg(22×) | |
|---|---|
| p2(222) | |
 |  |
| 4-162 원시 단위 | |
 c = e B + D = 180° | 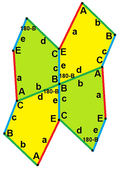 c = e, d = b B + D = 180° |
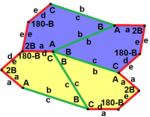
3, 4, 5종류
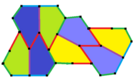
| 형식 3. | 타입 4 | 5타입 | ||||
|---|---|---|---|---|---|---|
| p3(333) | p31m(3*3) | p4(442) | p4g (4*2) | p6 (632) | ||
 |  |  |  |  |  | |
 |  |  | ||||
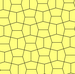| 3극 원단위 | 4-162 원시 단위 | 6-162 원시 단위 | 18세기 원시 단위 | |||
 a = b, d = c + e A = C = D = 120° | 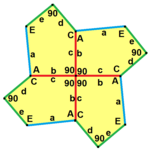 b = c, d = e B = D = 90° | 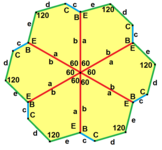 a = b, d = e A = 60°, D = 120° |  a = b = c, d = e A = 60°, B = 120°, C = 90° D = 120° E = 150° | |||
커슈너(1968) 유형 6, 7, 8
커슈너(1968)는 3종의 오각형 타일을 추가로 발견해 총 8종을 만들었다. 그는 이것이 비행기를 타일로 만들 수 있는 펜타곤의 전체 목록이라고 잘못 주장했다.
이러한 예는 2면체 및 가장자리 대 가장자리 입니다. 7타입과 8타입은 치랄쌍의 타일을 가지고 있는데, 이는 황록색-녹색 쌍으로, 다른 타입은 청색의 두 가지 색조로 채색된다. 키랄 쌍이 구별되는 것으로 간주될 때 pgg 대칭은 p2로 감소한다.
| 6타입 | 6타입 (또한 5타입) | 7타입체 | 8타입 | |
|---|---|---|---|---|
| p2(222) | pgg(22×) | pgg(22×) | ||
| p2(222) | p2(222) | |||
 |  |  |  | |
 |  |  | ||
a = d = e, b = c B + D = 180°, 2B = E |  a = d = e, b = c, B = 60° A = C = D = E = 120° | b = c = d = e B + 2E = 2C + D = 360° | b = c = d = e 2B + C = D + 2E = 360° | |
 4-162 원시 단위 |  4-162 원시 단위 |  8극 원단위 |  8극 원단위 | |
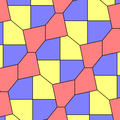
제임스(1975)타입 10
1975년 리차드 E. 제임스 3세는 1975년 7월 사이언티픽 아메리칸 잡지의 마틴 가드너의 '수학적 게임' 칼럼에서 커슈너의 결과를 읽은 후(가드너(1988)에 다시 게재되었다) 9번째 유형을 발견했다.[8] 그것은 유형 10으로 색인되어 있다. 타일링은 3면체, 비엣지(non-to-edge)
| p2(222) | cmm(2*22) |
|---|---|
 |  |
 | |
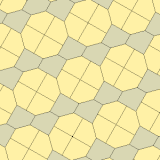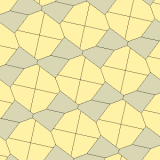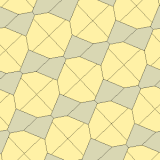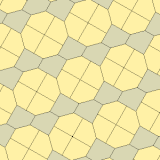a = b = c + e A=90, B+E=180° B + 2C = 360° | 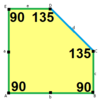 a=b=2c=2e A=B=E=90° C=D=135° |
 6-162 원시 단위 | |
쌀(1977) 유형 9,11,12,13
아마추어 수학자인 마조리 라이스는 1976년과 1977년에 새로운 테셀링 펜타곤 4종을 발견했다.[7][9]
4개의 틸팅은 모두 2면체다. 치랄 한 쌍은 등면 세트의 경우 노란색과 녹색으로, 다른 한 쌍은 파란색 두 가지 색조로 칠해져 있다. 키랄 쌍이 구별되는 것으로 간주될 때 pgg 대칭은 p2로 감소한다.
9타입의 타일링은 가장자리부터 가장자리까지이지만 다른 타일들은 그렇지 않다.
각 원시 단위에는 8개의 타일이 들어 있다.
| 9타입 | 11식 | 12타입체 | 13식 |
|---|---|---|---|
| pgg(22×) | |||
| p2(222) | |||
 |  |  |  |
 |  |  |  |
b = c = d = e 2A + C = D + 2E = 360° | 2a + c = d = e A = 90°, 2B + C = 360° C + E = 180° | 2a = d = c + e A = 90°, 2B + C = 360° C + E = 180° | d = 2a = 2e B=E=90°, 2A+D=360° |
 8극 원단위 |  8극 원단위 |  8극 원단위 |  8극 원단위 |
스타인(1985)타입 14
1985년 롤프 스타인에 의해 14번째 볼록한 오각형이 발견되었다.[10]
타일링은 3면체, 비엣지(non-to-edge) 자유도 없이 타일을 완전히 정했다. The exact proportions are specified by and angle B obtuse with . Other relations can easily be deduced.
원시 단위에는 각각 6개의 타일이 들어 있다. 그것은 p2(222) 대칭을 가지고 있다.
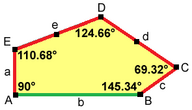 | 2a = 2c = d = e A=90°, B≈145.34°, C ≈ 69.32° D ≈ 124.66°, E ≈ 110.68° (2B + C = 360°, C + E = 180°) | 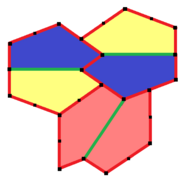 6-162 원시 단위 |
Mann/McLoud/Von Derau(2015) 유형 15
워싱턴 보첼 대학의 수학자 케이시 맨, 제니퍼 맥라우드만, 데이비드 폰 데라우는 컴퓨터 알고리즘을 사용하여 2015년에 15번째 단면 타일링 볼록 펜타곤을 발견했다.[11][12] 3면체 및 비엣지(non-edge)로, 3면체 위치의 치랄 쌍을 나타내는 6색, 3면체 2색으로 그려졌다. 키랄 쌍이 구별되는 것으로 간주될 때 pgg 대칭은 p2로 감소한다. 자유도 없이 타일을 완전히 정했다. 원시 단위에는 각각 12개의 타일이 들어 있다. 치랄 쌍이 구별되는 경우 pgg(22×) 대칭과 p2(222) 대칭이 있다.
2017년 7월, Michaell Rao는 비행기를 타일링할 수 있는 다른 종류의 볼록 펜타곤이 없다는 것을 보여주는 컴퓨터 보조 증거를 완성했다. 평면 타일을 할 수 있는 볼록 폴리곤의 전체 목록은 위의 15개의 펜타곤, 3개의 육각형, 그리고 모든 사분면 및 삼각형을 포함한다.[5] 위의 모든 유형이 정기적인 타일링을 허용하기 때문에 이 증명의 결과는 평면 타일을 주기적으로만 배열하는 볼록한 다각형이 존재하지 않는다는 것이다.
(더 큰 이미지) | A=c=e, b=2a,d=.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac.num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output.sfrac .den{border-top:1px 고체.}.mw-parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}a+√2/√3-1 A=150°, B=60°, C = 135° D=105°, E=90° | 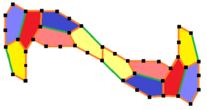 12구경 원시 단위 |
비주기적 단면 펜타곤 기울기
마이클 허쉬혼이 6배 회전 대칭으로 아래 예처럼 비주기적 단면 오각형 기울기도 구성할 수 있다. 각도는 A = 140°, B = 60°, C = 160°, D = 80°, E = 100°[13][14]
2016년에 Bernhard Klaassen은 모든 이산형 회전 대칭 유형이 동일한 등급의 펜타곤의 단면 오각형 타일링으로 표현될 수 있음을 보여줄 수 있었다.[15] 5배 대칭과 7배 대칭의 예는 다음과 같다. 그러한 틸링은 n>2와 함께 어떤 종류의 n-폴드 회전 대칭에도 가능하다.
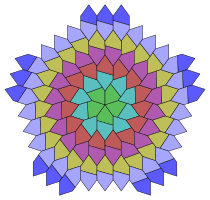 단면 오각형 타일링의 5배 회전 대칭 |  허쉬혼의 6배 회전 대칭 단면 오각형 타일링 |  단면 오각형 타일링에서 7배 회전 대칭 |
듀얼 유니폼 틸팅
등면 오각형 기울기는 균일 틸팅의 이중으로 생성되는 3개의 등면 오각형 기울기가 있다. 위 15개 단면 기울기의 대칭이 특별히 높은 경우를 나타낸다. 획일적인 틸팅과 그 듀얼은 모두 최첨단이다. 이러한 이중 기울기는 라브스 기울기라고도 한다. 균일 이중 기울기의 대칭은 균일 기울기와 동일하다. 균일한 기울기는 등각이기 때문에 이중은 등면이다.
| cmm(2*22) | p4g (4*2) | p6 (632) |
|---|---|---|
 |  |  |
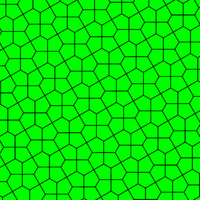| 프리즘 오각형 타일링 유형[16] 1의 인스턴스 | 카이로 오각형 타일링 유형[16][17] 4의 인스턴스 | 플레어트 오각형 타일링 유형 1, 5, 6의[16] 인스턴스 |
 120°, 120°, 120°, 90°, 90° V3.3.3.4.4 | 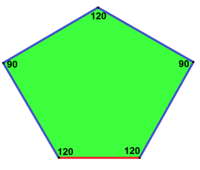 120°, 120°, 90°, 120°, 90° V3.3.4.3.4 | 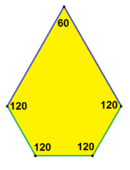 120°, 120°, 120°, 120°, 60° V3.3.3.3.6 |
이중 k-균일 틸팅
valence-5 꼭지점이 있는 k-uniform 틸팅도 오각형 이중 기울기를 가지며, 위의 반정형 이중과 동일한 세 가지 모양의 오각형을 포함하고 있지만 오각형의 혼합물을 포함하고 있다. k-uniform tiling은 k-isohedral 이중 타일링을 가지며, 아래의 다양한 색상과 색조로 표현된다.
예를 들어, 이러한 2, 3, 4, 5개의 통일된 이중은 모두 오각형이다.[18][19]
| 2면체의 | 3면체의 | |||
|---|---|---|---|---|
| p4g (4*2) | pgg(22×) | p2(222) | p6 (*632) | |
 |  |  |  |  |
| | | | | |
| 4면체의 | 5면체의 | |||
| pgg(22×) | p2(222) | p6m(*632) | ||
 |  |  |  |  |
| | | | | |
| 5면체의 | ||||
| pgg(22×) | p2(222) | |||
 |  |  |  |  |
| | | | | |
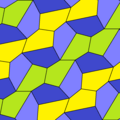
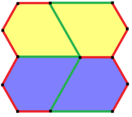
오각형/헥사각형 테셀레이션
펜타곤은 육각형과 독특한 관계를 가지고 있다. 아래에 그래픽으로 설명했듯이, 일부 유형의 육각형은 펜타곤으로 세분될 수 있다. 예를 들어, 일반 육각형은 두 가지 타입 1 펜타곤으로 이등분한다. 볼록 육각형은 3개(타입 3) 4개(타입 4) 9개(타입 3) 펜타곤으로도 분할이 가능하다.
이 관계의 확장에 의해, 평면은 육각형 오버레이를 발생시키는 방법으로 하나의 오각형 원형 모양으로 테셀링될 수 있다. 예를 들면 다음과 같다.
 일반 육각형(각각 2개의 펜타곤으로 구성)의 오버레이가 있는 단일 오각형 프로토타일(유형 1)에 의한 평면 테셀레이션. |  일반 육각형(각각 3개의 펜타곤으로 구성)의 오버레이가 있는 단일 오각형 프로토타일(타입 3)에 의한 평면 테셀레이션. |  반정형 육각형(각각 4개의 펜타곤으로 구성됨)의 오버레이가 있는 단일 오각형 프로토타일(타입 4)에 의한 평면 테셀레이션. |  두 가지 크기의 일반 육각형(각각 3개 및 9개 펜타곤)의 오버레이를 가진 단일 오각형 프로토타일(타입 3)에 의한 평면 테셀레이션. |
비콘벡스 펜타곤
볼록할 필요가 없는 펜타곤으로, 추가적인 타일링이 가능하다. 예를 들어, 오각형 재타일에 의해 형성된 주기적인 타일링인 스핑크스 타일링이 있다.[20] 스핑크스는 또한 주기적으로 두 개의 스핑크스 타일을 함께 장착하여 평행사변형을 이룬 다음 이 평행사변형을 해석하여 평면을 타일링할 수 있는데,[20] 이는 2㎛에 이르는 연속 각도를 갖는 비콘벡스 펜타곤으로 확장될 수 있는 패턴으로 위의 볼록형 1형의 조건을 만족시킬 수 있다.
정삼각형을 삼각형의 중심에서 만나는 세 개의 합칭 비콘벡스 펜타곤으로 나눌 수 있으며, 그 결과 3펜타곤 단위로 평면을 타일로 묶을 수 있다.[21] 비슷한 방법을 사용하여 정사각형을 4개의 합금 비합금 펜타곤으로 세분하거나, 정규 육각형을 6개의 합금 비합금 펜타곤으로 분할한 다음, 그 결과 단위를 사용하여 평면을 타일로 배열할 수 있다.
비유클리드 기하학에서 규칙적인 오각형 기울기
도데카헤드론은 슐레플리 기호 {5,3}이(가) 각 꼭지점 주위에 3개의 펜타곤이 있는 구 표면에 12개의 펜타곤의 정규 타일링으로 간주할 수 있다.
쌍곡면에는 일반 펜타곤 기울기가 있는데, 예를 들어 오더-4 오각형 타일링, {5,4}, 각 꼭지점 주위에 4개의 펜타곤이 있다. 고차 정규 기울기 {5,n}은(는) 쌍곡면에 생성될 수 있으며, 이는 {5,610}(으)로 종료된다.
| 구 | 쌍곡면 | |||||
|---|---|---|---|---|---|---|
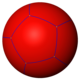 {5,3} |  {5,4} |  {5,5} |  {5,6} |  {5,7} |  {5,8} | ...{5,∞} |
불규칙한 쌍곡면 오각형 기울기
등각 불규칙한 오각형 얼굴을 가진 쌍곡면에는 무한히 많은 이중 제복 기울기가 있다. 그들은 V3.3.p.3.p.3.q와 같은 얼굴 구성을 가지고 있다.
| 7-3 | 8-3 | 9-3 | ... | 5-4 | 6-4 | 7-4 | ... | 5-5 |
|---|---|---|---|---|---|---|---|---|
 V3.3.3.3.7 |  V3.3.3.3.8 | V3.3.3.3.9 | ... |  V3.3.4.3.5 | V3.3.4.3.6 | V3.3.4.3.7 | ... | V3.3.5.3.5 |
이항 타일링은 호로사이클릭 가장자리를 선 세그먼트별로 교체할 경우 오각형 타일링으로 만들 수 있다.
참조
- ^ Chung, Ping Ngai; Fernandez, Miguel A.; Li, Yifei; Mara, Michael; Morgan, Frank; Plata, Isamar Rosa; Shah, Nirlee; Vieira, Luis Sordo; Wikner, Elena (2012-05-01). "Isoperimetric Pentagonal Tilings". Notices of the American Mathematical Society. 59 (05): 632. doi:10.1090/noti838. ISSN 0002-9920.
- ^ 그룬바움 & 셰퍼드 1987, 제9.3절 볼록 폴리곤에 의한 기타 단면 기울기
- ^ 라오 2017.
- ^ "Mathematica code verifying Rao-convex-pentagon-tiling classification", GitHub
- ^ a b 월초버 2017.
- ^ 그룬바움 & 셰퍼드 1978.
- ^ a b 샤츠슈나이더 1978.
- ^ 마조리 라이스의 비밀 펜타곤 콴타 매거진
- ^ Marjorie Rice, "Tessellations", Intriguing Tessellations, retrieved 22 August 2015 – via Google Sites
- ^ 샤츠슈나이더 1985.
- ^ 벨로스 2015.
- ^ Mann, McLoud-Mann & Von Derau 2018.
- ^ 샤츠슈나이더 1978, 그림 12.
- ^ 허쉬혼 & 헌트 1985.
- ^ 클라센 2016.
- ^ a b c 라인하르트 1918, 페이지 77–81 (주의: 이 논문에는 적어도 하나의 명백한 실수가 있다. 즉, 77페이지에 정의된 처음 2개의 타일링 형식에 대해 π+Δ 각도 합계가 2π가 아니라 π과 같아야 한다.)
- ^ wolframalpha.com의 펜타곤 타입 4 쿼리와 펜타곤 타입 2 타일링 쿼리에 의해 생성된 카이로 펜타곤 타입 2 타일링의 울프램 정의가 1918년 라인하르트가 정의한 타입 2와 일치하지 않음)
- ^ 채비 1989년
- ^ Brian Galebach, "Welcome to my collection of n-uniform tilings!", probabilitysports.com
- ^ a b 고드레슈 1989.
- ^ 게버 2003.
참고 문헌 목록
- Bagina, Olga (2004), "Tiling the plane with congruent equilateral convex pentagons", Journal of Combinatorial Theory, Series A, 105 (2): 221–232, doi:10.1016/j.jcta.2003.11.002, ISSN 1096-0899, MR 2046081
- Bagina, Olga (2011), Мозаики из выпуклых пятиугольников [Tilings of the plane with convex pentagons], Vestnik (in Russian), 4 (48): 63–73, ISSN 2078-1768, retrieved 29 January 2013
- Bellos, Alex (11 August 2015), "Attack on the pentagon results in discovery of new mathematical tile", The Guardian
- Chavey, D. (1989), "Tilings by Regular Polygons—II: A Catalog of Tilings", Computers & Mathematics with Applications, 17 (1–3): 147–165, doi:10.1016/0898-1221(89)90156-9
- Gardner, Martin (1988), "Tiling with Convex Polygons", Time travel and other mathematical bewilderments, New York: W.H. Freeman, Bibcode:1988ttom.book.....G, ISBN 978-0-7167-1925-0, MR 0905872
- Gerver, M. L. (2003), "Theorems on tessellations by polygons", Sbornik: Mathematics, 194 (6): 879–895, Bibcode:2003SbMat.194..879G, doi:10.1070/sm2003v194n06abeh000743
- Godrèche, C. (1989), "The sphinx: a limit-periodic tiling of the plane", Journal of Physics A: Mathematical and General, 22 (24): L1163–L1166, Bibcode:1989JPhA...22L1163G, doi:10.1088/0305-4470/22/24/006, MR 1030678
- Grünbaum, Branko; Shephard, Geoffrey C. (1978), "Isohedral tilings of the plane by polygons", Commentarii Mathematici Helvetici, 53: 542–571, doi:10.1007/bf02566098, ISSN 0010-2571
- Grünbaum, Branko; Shephard, Geoffrey C. (1987), "Tilings by polygons", Tilings and Patterns, New York: W. H. Freeman and Company, ISBN 978-0-7167-1193-3, MR 0857454
- Hirschhorn, M. D.; Hunt, D. C. (1985), "Equilateral convex pentagons which tile the plane" (PDF), Journal of Combinatorial Theory, Series A, 39 (1): 1–18, doi:10.1016/0097-3165(85)90078-0, ISSN 1096-0899, MR 0787713, retrieved 2020-10-30
- Kershner, Richard (1968), "On paving the plane", American Mathematical Monthly, 75 (8): 839–844, doi:10.2307/2314332, ISSN 0002-9890, JSTOR 2314332, MR 0236822
- Klaassen, Bernhard (2016), "Rotationally symmetric tilings with convex pentagons and hexagons", Elemente der Mathematik, 71 (4): 137–144, arXiv:1509.06297, doi:10.4171/em/310, ISSN 0013-6018
- Mann, Casey; McLoud-Mann, Jennifer; Von Derau, David (2018), "Convex pentagons that admit -block transitive tilings", Geometriae Dedicata, 194 (1): 141–167, arXiv:1510.01186, doi:10.1007/s10711-017-0270-9
- Rao, Michaël (2017), Exhaustive search of convex pentagons which tile the plane (PDF), arXiv:1708.00274
- Reinhardt, Karl (1918), Über die Zerlegung der Ebene in Polygone (Dissertation) (in German), Borna-Leipzig: Druck von Robert Noske
- Schattschneider, Doris (1978), "Tiling the plane with congruent pentagons", Mathematics Magazine, 51 (1): 29–44, doi:10.2307/2689644, ISSN 0025-570X, JSTOR 2689644, MR 0493766
- Schattschneider, Doris (1985), "A new pentagon tiler", Mathematics Magazine, 58 (5): 308, The cover has a picture of the new tiling
- Sugimoto, Teruhisa; Ogawa, Tohru (2005), "Systematic study of convex pentagonal tilings. I. Case of convex pentagons with four equal-length edges", Forma, 20: 1–18, MR 2240616
- Sugimoto, Teruhisa; Ogawa, Tohru (2009), "Systematic study of convex pentagonal tilings, II: tilings by convex pentagons with four equal-length edges", Forma, 24 (3): 93–109, MR 2868775; 에라타, 포마 25 (1): 49, 2010, MR2868824
- Sugimoto, Teruhisa (2012), "Convex pentagons for edge-to-edge tiling, I", Forma, 27 (1): 93–103, MR 3030316
- Wolchover, Natalie (11 July 2017), "Pentagon Tiling Proof Solves Century-Old Math Problem", Quanta Magazine
외부 링크
 | 위키미디어 커먼스는 펜타곤 기울기와 관련된 미디어를 보유하고 있다. |
- Weisstein, Eric W., "Pentagon Tiling", MathWorld
- 펜타곤 틸링스
- 평면 타일을 그리는 14개의 펜타곤
- 15 (단면) k-이소 색상이 있는 볼록한 오각형 타일을 가진 기울기
- 14번째 펜타곤 유형 타일링 표시 코드
- 15번째 펜타곤 유형 타일링 표시 코드
.png){kind=link}