오일러 벽돌

수학에서 오일러 벽돌은 레온하르트 오일러의 이름을 딴 직사각형의 입체형이며, 가장자리와 얼굴 대각선은 모두 정수 길이를 가지고 있다. 원시 오일러 벽돌은 가장자리 길이가 비교적 가장 긴 오일러 벽돌이다. 완벽한 오일러 벽돌은 가장 긴 대각선 공간도 정수지만 그런 벽돌은 아직 발견되지 않았다.

가장자리

a,

b,

c

및 면 대각선

d,

e,

f

가 있는 오일러 벽돌

정의

기하학적 용어로 오일러 벽돌의 정의는 다음과 같은 디오판타인 방정식의 시스템에 대한 해법과 동등하다.

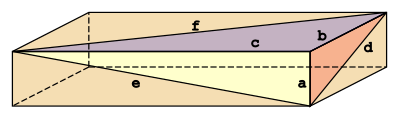
{\displaysty}a^{2}+b^{2}}=d^{2}\\a^{2}+c^{2}}}=e^{2}\b^{2}+c^{2}=f^{2}\end{case}}}}}

여기서 $a,$ $b,$ $c$ 는 가장자리, $d,$ $e,$ $f$ 는 대각선이다.

특성.

$(a,$ $b,$ $c)$ 가 해결책이라면, ( $ka,$ $kb,$ $kc)$ 도 $어떤$ k에 대한 해결책이다. 따라서 합리적인 숫자의 해법은 모두 정수 해법의 재계산이다. 가장자리 길이 $(a,$ $b,$ $c$ )가 있는 오일러 벽돌을 보면 $,$ 3중 $(bc,$ $ac,$ $ab)$ 도 오일러 벽돌을 구성한다.^[1]^{: p. 106}

오일러 벽돌의 적어도 두 모서리는 3으로 나눌 수 있다.^[1]^{: p. 106}

오일러 벽돌의 적어도 두 모서리는 4로 나눌 수 있다.^[1]^{: p. 106}

오일러 벽돌의 적어도 하나의 가장자리는 11로 나눌 수 있다.^[1]^{: p. 106}

예

1719년 폴 핼케에 의해 발견된 가장 작은 오일러 벽돌은 가장자리 $(a,$ $b,$ $c)$ = $(44, 117,$ $240$ $)$ 와 얼굴 대각선 $(d,$ $e,$ f ) = ( $125$ , $244, 267$ )이 있다 $.$ ^[2] 가장자리 $(a,$ $b,$ $c)$ — 면 대각선 $(d,$ e, $f)$ 으로 주어진 다른 작은 원시적 해법은 다음과 같다.

크기가 1000 이하인 원시 오일러 벽돌 5개 모두

(	85,	132,	720	) — (	157,	725,	732	)
(	140,	480,	693	) — (	500,	707,	843	)
(	160,	231,	792	) — (	281,	808,	825	)
(	187,	1020,	1584	) — (	1037,	1595,	1884	)
(	195,	748,	6336	) — (	773,	6339,	6380	)
(	240,	252,	275	) — (	348,	365,	373	)
(	429,	880,	2340	) — (	979,	2379,	2500	)
(	495,	4888,	8160	) — (	4913,	8175,	9512	)
(	528,	5796,	6325	) — (	5820,	6347,	8579	)

수식생성중

오일러는 이 문제에 대한 최소 두 개의 파라메트릭 솔루션을 찾았지만 어느 것도 모든 해결책을 제공하지 않는다.^[3]

사운더슨의 파라메트릭 [4] 공식으로 많은 오일러 벽돌을 만들 수 있다. $(u,$ $v,$ $w)$ 피타고라스 3중(즉, $u 2 2$ + v = $w 2$ .) 그^[1]^{: 105} 다음 가장자리

a=u 4v^{2}-w^{2},\cHB=v 4u^{2}-w^{2},\HB c=4uvw

얼굴을 대각선으로 비추다

d=w^{3},\property e=u(4v^{2}+w^{2}),\properties f=v(4u^{2}+w^{2})).

위와 같이 파라메트리되지 않은 오일러 벽돌 $(a,$ $b,$ $c) =$ $(240, 252, 275)$ 및 얼굴 대각선 $(d,$ $e$ , $f)$ $=$ $(348, 365, 373$ ) 등이 있다 $.$

퍼펙트 큐보이드

수학의 미해결 문제:

완벽한 입체감이 존재하는가?

(수학에서 더 풀리지 않은 문제)

완벽한 큐보이드(완벽한 오일러 벽돌, 완벽한 상자라고도 함)는 대각선 공간도 정수 길이가 있는 오일러 벽돌이다. 즉, 오일러 벽돌을 정의하는 디오판틴 방정식 시스템에 다음과 같은 방정식이 추가된다.

a^{2}+b^{2}+c^{2}}}=g^{2},

여기서 $g$ 는 대각선 공간이다. 2020년^[update] 9월 현재, 완벽한 큐보이드의 예는 발견되지 않았고 아무도 존재하지 않는다는 것을 증명하지 못했다.^[5]

가장자리

a,

b,

c

및 면 대각선

d,

e,

f

가 있는 오일러 벽돌

컴퓨터 검색 결과 완벽한 큐보이드가 존재한다면

홀수 가장자리는 2.5 × 10보다¹³ 커야 한다.^[5]
가장 작은 가장자리는 5×10보다¹¹ 커야 한다.^[5]

모듈식 산수에 기초하여 원시적인 완벽한 입체형(존재하는 경우)에 의해 충족되어야 하는 속성에 대해 다음과 같은 사실이 알려져 있다.^[6]

한쪽 가장자리, 두 개의 얼굴 대각선 및 몸통 대각선은 홀수여야 하며, 한쪽 가장자리와 나머지 얼굴 대각선은 4로 분할해야 하며, 나머지 가장자리는 16으로 분할해야 한다.
두 가장자리의 길이는 3으로 나누어져야 하며, 이들 가장자리 중 적어도 하나는 9로 나누어져야 한다.
한쪽 가장자리에는 5로 나눌 수 있는 길이가 있어야 한다.
한쪽 가장자리에는 7로 나눌 수 있는 길이가 있어야 한다.
한쪽 가장자리에는 11로 나눌 수 있는 길이가 있어야 한다.
한쪽 가장자리에는 19로 나눌 수 있는 길이가 있어야 한다.
하나의 가장자리 또는 공간 대각선은 13으로 분할해야 한다.
한쪽 가장자리, 면 대각선 또는 공간 대각선은 17로 분할해야 한다.
한쪽 가장자리, 면 대각선 또는 공간 대각선은 29로 분할해야 한다.
한쪽 가장자리, 면 대각선 또는 공간 대각선은 37로 분할해야 한다.

추가 사항:

대각선 공간은 1차 동력도 아니고 2차원의 산물도 아니다.^[7]^{: p. 579}
대각선 공간은 div 1(mod 4)만 포함할 수 있다.^[7]^{: p. 566}^[8]

큐보이드 추측

3개의 입체파 추측이란 여러 정수 매개변수에 따라 정수 계수를 갖는 3개의 일변수 다항식을 다시 해석할 수 없다고 주장하는 3개의 수학 명제다. 그 추측들은 완벽한 입체파 문제와 관련이 있다.^[9]^[10] 완벽한 큐보이드 문제와 동등하지는 않지만, 이 세 가지 추측이 모두 타당하다면, 완벽한 큐보이드는 존재하지 않는다. 그들은 증명하지도 반증하지도 않았다.

큐보이드 추측 1. 임의의 2개의 양의 복사 정수 $\displaystyle a\neq u$ {\ $displaystyle \displaystyle a\neq$ u $}$ 8도 $\displaystyle a\neq u$ 다항식

P_{au}(t)=t^{8}+6\,(u^{2}-a^{2})\,t^{6}+(a^{4}-4\,a^{2}\,u^{2}+u^{4})\,t^{4}-6\,a^{2}\,u^{2}\,(u^{2}-a^{2})\,t^{2}+u^{4}\,a^{4}

(1)

정수 $\displaystyle \mathbb {Z}$ ${\$ 의 링 위에서 설명할 수 없다 $\displaystyle \mathbb {Z}$

큐보이드 추측 2. 임의의 2개의 양의 coprime 정수 p $\displaystyle p\neq q$ ${\$ 10도 $\displaystyle p\neq q$ 다항식

{\displaystyle{\begin{정렬}(t)={}&, t^ᆶ+ᆭᆮt^ᆷ\\[4pt]&,{}[4pt]&,{}[4pt]&,{}[4pt]&,{}-q^{10}\,p^{10}\end{정렬}}}

(2)

정수 $\displaystyle \mathbb {Z}$ ${\$ 의 링 위에서 설명할 수 없다 $\displaystyle \mathbb {Z}$

큐보이드 추측 3. 임의의 양의 복사수 정수 3개에 대해 $\displaystyle a$ ${\$ $\displaystyle b$ ${\$ $\displaystyle u$ ${\$ 조건 $\displaystyle u$ 없음

{\begin{array}{lcr}{\text{1)}}\qquad a=b;\qquad \qquad &{\text{3)}}\qquad b\,u=a^{2};\qquad \qquad &{\text{5)}}\qquad a=u;\\{\text{2)}}\qquad a=b=u;\qquad \qquad &{\text{4)}}\qquad a\,u=b^{2};\qquad \qquad &{\text{6)}}\qquad b=u\end{array}}

(3)

12도 다항식인 충족됨

{\reasoned}P_ᆭ(t)={}&, t^ᆯ+(6u^{2}-2a^{2}-2b^{2})t^{10}\\&,{}(u^{4}+b^{4}+a^{4}+4a^{2}u^{2}+4b^{2}u^{2}-12b^{2}a^{2})t^{8}\\&,{}(6a^{4}u^{2}+6u^{2}b^{4}-8a^{2}b^{2}u^{2}-2u^{4}a^{2}-2u^{4}b^{2}-2a^{4}b^{2}-2b^{4}a^{2})t^{6}\\&,{}(4u^{2}b^{4}a^{2}+4a^{4}u^{2}b^{2}-12u^{4}a^{2}b^{2}+u^{4}a^{4}+u^{4}b^{4}+a^{4}b^{4})t^{4}\\&,{}+(6a^{4}u^{2}b^{4}-2u^{4}a^{4}b^{2}-2u^{4}a^{2}b^{4}}t^{2}+u^{4}a^{4}b^{4}.\end{정렬}}

(4)

정수 $\displaystyle \mathbb {Z}$ ${\$ 의 링 위에서 설명할 수 없다 $\displaystyle \mathbb {Z}$

거의 완벽한 큐보이드

거의 완벽한 큐빅은 7개의 길이 중 6개를 합리적인 길이만큼 가지고 있다. 그러한 큐보이드들은 바디, 에지, 페이스 큐보이드라고 불리는 세 가지 유형으로 분류될 수 있다.^[11]

바디 큐보이드의 경우 몸(공간) 대각선 $g$ 가 비이성적이다. 에지 큐보이드의 경우 가장자리 $a,$ $b,$ c 중 $하나$ 가 비이성적이다. 페이스 큐보이드에는 얼굴 대각선 $d,$ $e,$ $f$ 비이성 중 하나뿐입니다.

보디 큐보이드(Body cuboid)는 이러한 유형의 큐보이드에 대해 논의한 레오나드 오일러를 기리기 위해 일반적으로 오일러 큐보이드(Uler cuboid)라고 불린다.^[12] 그는 페이스 큐보이드에 대해서도 알고 있었고, (104, 153, 672)의 예를 제공했다.^[13] 면 큐보이드의 3정수 큐보이드 가장자리 길이와 3정수의 대각선 길이는 또한 Schléfli Orthoscheme인 헤로니아 4면체의 가장자리 길이로 해석될 수 있다. 얼굴 큐보이드도 무한히 많고, 헤로니아 정형도 무한히 많다.^[14]

단지 최근에 와서야 복잡한 숫자의 큐보이드들이 알려지게 되었다.

랜달^[update] L. 래스번은 2017년 9월 현재 정수 가장자리가 가장 작은 큐보이드 15만5151개를 발견했으며^[15], 정수 가장자리가 1억5700만개 미만인 큐보이드 56만75개는 오일러(바디) 큐보이드, 숫자 가장자리 길이가 복잡한 에지 큐보이드 15만449개, 에지 큐보이드 30만81개, 페이스 큐보이드 5만3046개가 발견됐다.

에지, 면 대각선 및 공간 대각선 $(a,$ $b,$ $c,$ $d,$ $e,$ $f,$ $g$ )으로 주어진 거의 완벽한 큐보이드의 각 유형에 대한 가장 작은 솔루션 $:$

차체 큐빅: $(44, 117, 240, 125$ , $244, 267,$ $\sqrt 73225)$
에지 큐보이드: $(520, 576,$ $\sqrt 618849, 776, 943, 975, 1105)$
면 큐보이드 $:$ ( $104, 153$ , $672, 185, 680$ , $47474993, 697)$
복합체 큐보이드 $:$ ( $63i, 60i, 65, 87i, 16, 25, --3344)$
복합 모서리 큐보이드 $:$ ( $1968-3344, 60, 63, 16, 25, 87, 65)$
복합면체 큐보이드: $(672i, 153i, 697,$ $\sqrt- 474993$ , $185, 680, 104$ )

완벽한 평행선

완벽한 평행은 정수 길이 가장자리, 얼굴 대각선, 신체 대각선으로 이루어진 평행선이다. 그러나 모든 직각으로 이루어진 것은 아니다. 완벽한 입체형은 완전 평행선인 특별한 경우다. 2009년에는 리차드 가이(Richard Guy)의 공개 질문에 ^[16]답하면서 수십 개의 완벽한 평행선 동물이 존재하는 것으로 나타났다. 이 완벽한 평행선 중 몇몇은 두 개의 직사각형 얼굴을 가지고 있다. 가장 작은 완벽한 평행선에는 가장자리 271, 106, 103이 있고, 짧은 얼굴 대각선 101, 266, 255가 있으며, 긴 얼굴 대각선 183, 312, 323이 있으며, 몸 대각선 374, 300, 278, 272가 있다.

참고 항목

피타고라스 4배

메모들

^ ^a ^b ^c ^d ^e Wacwaw Sierpiński, Phinagorean Triangles, Dover Publishes, 2003(원산지). 1962년 개정.
^ Infinity의 비전: 17장 이안 스튜어트의 위대한 수학 문제
^ Weisstein, Eric W. "Euler Brick". MathWorld.
^ Knill, Oliver (February 24, 2009). "Treasure Hunting Perfect Euler bricks" (PDF). Math table. Harvard University.
^ ^a ^b ^c Matson, Robert D. "Results of a Computer Search for a Perfect Cuboid" (PDF). unsolvedproblems.org. Retrieved February 24, 2020.
^ M. Kraitchik, On Rational Cuboids, Scripta Mathematica, 제11권 (1945년)
^ ^a ^b I. Koreec, 완벽한 이성 큐보이드의 하한선, 수학. 슬로바카, 42세 (1992년), 5번, 565-582페이지.
^ 2000년 6월 로널드 판 루이크 온 퍼펙트 큐보이드
^ Sharipov R.A. (2012). "Perfect cuboids and irreducible polynomials". Ufa Math Journal. 4 (1): 153–160. arXiv:1108.5348. Bibcode:2011arXiv1108.5348S.
^ Sharipov R.A. (2015). "Asymptotic approach to the perfect cuboid problem". Ufa Math Journal. 7 (3): 100–113.
^ Rathbun R. L, Granlund Ⅱ, 본문, 가장자리 및 얼굴 유형의 솔루션 // 수학이 포함된 정수 큐보이드 테이블. 1994년 6권, 페이지 441-442.
^ 오일러, 레오나드, 볼스트산디게 안레이퉁 주르 대수, 카이세를리히헤 아카데미에 데르 위센샤프텐, 상트페테르부르크, 1771년
^ 오일러, 레너드, 볼스트산디게 안레이퉁 주르 대수, 2, 2부 236, 영어 번역: 오일러, 대수학 원소, 스프링거-베를라크 1984
^ "Problem 930" (PDF), Solutions, Crux Mathematicorum, 11 (5): 162–166, May 1985
^ Rathbun, Randall L. (16 November 2018). "The Integer Cuboid Table". arXiv:1705.05929v3 [math.NT].
^ Sawyer, Jorge F.; Reiter, Clifford A. (2011). "Perfect parallelepipeds exist". Mathematics of Computation. 80 (274): 1037–1040. arXiv:0907.0220. doi:10.1090/s0025-5718-2010-02400-7..

참조

Leech, John (1977). "The Rational Cuboid Revisited". American Mathematical Monthly. 84 (7): 518–533. doi:10.2307/2320014. JSTOR 2320014.
Shaffer, Sherrill (1987). "Necessary Divisors of Perfect Integer Cuboids". Abstracts of the American Mathematical Society. 8 (6): 440.
Guy, Richard K. (2004). Unsolved Problems in Number Theory. Springer-Verlag. pp. 275–283. ISBN 0-387-20860-7.
Kraitchik, M. (1945). "On certain rational cuboids". Scripta Mathematica. 11: 317–326.
Roberts, Tim (2010). "Some constraints on the existence of a perfect cuboid". Australian Mathematical Society Gazette. 37: 29–31. ISSN 1326-2297.

[Sierpinski-1] Wacwaw Sierpiński, Phinagorean Triangles, Dover Publishes, 2003(원산지). 1962년 개정.

[2] Infinity의 비전: 17장 이안 스튜어트의 위대한 수학 문제

[3] Weisstein, Eric W. "Euler Brick". MathWorld.

[Sounderson-4] Knill, Oliver (February 24, 2009). "Treasure Hunting Perfect Euler bricks" (PDF). Math table. Harvard University.

[Matson-5] Matson, Robert D. "Results of a Computer Search for a Perfect Cuboid" (PDF). unsolvedproblems.org. Retrieved February 24, 2020.

[6] M. Kraitchik, On Rational Cuboids, Scripta Mathematica, 제11권 (1945년)

[Korec-7] I. Koreec, 완벽한 이성 큐보이드의 하한선, 수학. 슬로바카, 42세 (1992년), 5번, 565-582페이지.

[8] 2000년 6월 로널드 판 루이크 온 퍼펙트 큐보이드

[shr_01-9] Sharipov R.A. (2012). "Perfect cuboids and irreducible polynomials". Ufa Math Journal. 4 (1): 153–160. arXiv:1108.5348. Bibcode:2011arXiv1108.5348S.

[shr_02-10] Sharipov R.A. (2015). "Asymptotic approach to the perfect cuboid problem". Ufa Math Journal. 7 (3): 100–113.

[11] Rathbun R. L, Granlund Ⅱ, 본문, 가장자리 및 얼굴 유형의 솔루션 // 수학이 포함된 정수 큐보이드 테이블. 1994년 6권, 페이지 441-442.

[12] 오일러, 레오나드, 볼스트산디게 안레이퉁 주르 대수, 카이세를리히헤 아카데미에 데르 위센샤프텐, 상트페테르부르크, 1771년

[13] 오일러, 레너드, 볼스트산디게 안레이퉁 주르 대수, 2, 2부 236, 영어 번역: 오일러, 대수학 원소, 스프링거-베를라크 1984

[14] "Problem 930" (PDF), Solutions, Crux Mathematicorum, 11 (5): 162–166, May 1985

[15] Rathbun, Randall L. (16 November 2018). "The Integer Cuboid Table". arXiv:1705.05929v3 [math.NT].

[16] Sawyer, Jorge F.; Reiter, Clifford A. (2011). "Perfect parallelepipeds exist". Mathematics of Computation. 80 (274): 1037–1040. arXiv:0907.0220. doi:10.1090/s0025-5718-2010-02400-7..

[1]

[2]

[3]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

Search

오일러 벽돌

네임스페이스

더

목차

정의

특성.

예

수식생성중

퍼펙트 큐보이드

큐보이드 추측

거의 완벽한 큐보이드

완벽한 평행선

참고 항목

메모들

참조